0 引言
第三代轮毂轴承属于非标准轴承,它通过两个法兰盘分别连接车轮和车身,预先调整游隙,采用摇辗技术施加预紧载荷,免维护,提高了使用寿命。目前轮毂轴承还没有成熟的理论指导设计,经验性的结论居多[1],因此本文开展第三代轮毂轴承内部载荷分布与弯曲疲劳寿命的理论研究与试验分析。
滚动轴承经典失效方式是滚道或滚动体的接触疲劳[2],对于接触表面光滑和弹性流体动压润滑条件下运行的滚动轴承,剥落是最主要的失效形式。目前,滚动轴承的接触疲劳寿命预测模型从机理上可以分为基于概率分布的寿命模型和基于断裂力学的寿命模型[3]。
1947年, LUNDBERG等[4]基于次表面正交切应力提出了L-P理论,并结合Weibull分布理论建立了轴承寿命的经验公式。长期以来,经典的L-P模型一直是国际上公认的滚动轴承寿命计算的基础[5]。很多学者基于L-P理论提出了修正或改进的模型。OSWALD等[6]将L-P轴承寿命理论扩展到了面点蚀的执行系统(包括接触载荷疲劳和轮齿弯曲疲劳)。PAULSON等[7]基于L-P理论建立了轴承损伤的有限元寿命模型,有效地预测了返修轴承寿命。
利用载荷分布计算轴承基本额定寿命的L-P 理论模型,虽然计算准确,但计算量较大,过程复杂[8],因此,经过国际标准 ISO281—2007简化的 L-P 寿命理论[9]被广泛应用于各个领域,成为各大轴承厂商普遍认可的轴承选型依据。然而,简化模型不能用于受弯矩作用轴承寿命的计算[10]。
滚动体载荷影响轴承的摩擦、润滑与寿命,因此计算载荷分布是轴承分析中不可缺少的内容。对于载荷分布的计算方法,文献[11]以深沟球轴承为对象建立了在纯径向力作用下轴承的动态接触模型。文献[12]以圆柱滚子轴承为研究对象,通过计算弹性半空间和有限元数值求解了Boussinesq问题。文献[13]用解析法和有限元法(FEM)确定球面滚子轴承的接触载荷,对两种方法在不同加载条件下的接触载荷进行了比较。文献[14]基于有限元法计算接触载荷的分布,并采用理论模型和接触压力传感器对有限元模型进行了校正。以上方法均是基于赫兹接触理论,文献[15-16]描述了在不确定接触状态情况下获取球轴承的力学行为,提出建立非赫兹接触模型的方法,并与赫兹接触模型的计算结果进行对比分析。
轮毂轴承在使用时,常采用填充润滑剂和机械密封来实现终生润滑,滚动体与滚道接触面之间的润滑膜避免了金属的直接接触,使得轴承的使用寿命得到了很大提高。TALLIAN[17]研究了润滑条件不同的情况下,滚动轴承的使用寿命与润滑油膜参数λ之间的关系,结果表明,提高润滑油膜参数λ可以成倍地提高滚动轴承的使用寿命。文献[18]结合 ISO281—2007 讨论了黏度比对 I-H 理论中应力寿命系数的影响,进而得到它对轴承寿命的影响,并分析了获得黏度比的不同方法,讨论了不同条件下计算黏度比的最佳方式。文献[19]基于边界润滑理论研究了轴承接触涂层滚动与滑动的摩擦学性能。文献[20]以球面滚子轴承为研究对象,在高径向载荷、恒定速度工况下研究了润滑对轴承寿命的影响。
国内外很多学者已经提出了径向力工况、轴向力工况和综合工况下的轴承滚道接触载荷的分布理论模型,由于车辆在实际运行工况下的三力联合作用(轴向、径向、弯矩)与纯弯矩作用下的轮毂轴承载荷分布规律一致,且在较高弯矩水平下最大接触载荷相差较小[21],因此为了与本文试验工况的边界条件相匹配,本文只考虑弯矩作用下的模型。
1 轮毂轴承的载荷分布
滚动体与滚道之间的接触载荷直接影响轴承的疲劳寿命,特别是轮毂轴承中受载最大的接触载荷对轴承的承载能力和疲劳寿命的影响最为显著[22]。因此,为了更加精确地预测第三代轮毂轴承的弯曲疲劳寿命,本文首先计算纯弯矩作用下的轮毂轴承载荷分布。由于载荷分布受游隙的影响较小,故忽略游隙的因素。第三代轮毂轴承的结构与性能参数如表1所示。
表1 轮毂轴承结构与性能参数
Tab.1 Structure and performance parameters of hub bearing
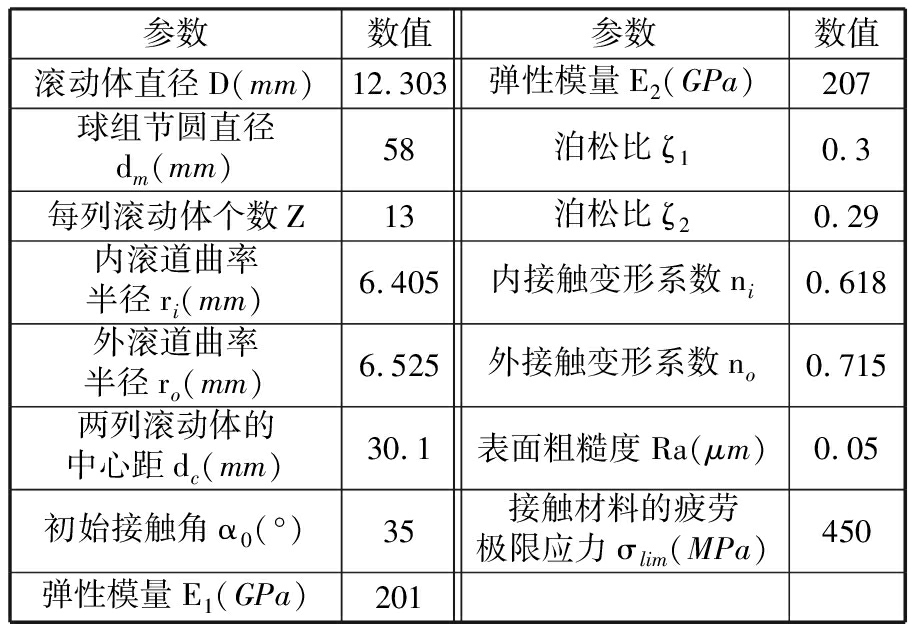
参数数值参数数值滚动体直径D(mm)12.303弹性模量E2(GPa)207球组节圆直径dm(mm)58泊松比ζ10.3每列滚动体个数Z13泊松比ζ20.29内滚道曲率半径ri(mm)6.405内接触变形系数ni0.618外滚道曲率半径ro(mm)6.525外接触变形系数no0.715两列滚动体的中心距dc(mm)30.1表面粗糙度Ra(μm)0.05初始接触角α0(°)35接触材料的疲劳极限应力σlim(MPa)450弹性模量E1(GPa)201
1.1 轮毂轴承受力分析
轮毂轴承所受的外部载荷是通过车轮间接施加的,轮毂轴承单元受径向力、轴向力和弯矩的共同作用[23]。
为了与后文的旋转弯曲疲劳试验的边界条件相吻合,本文建立汽车轮毂轴承只考虑弯矩的载荷分布模型。如图1所示,轮毂轴承的内法兰盘与制动盘相连,外法兰盘与车身相连,将轮胎在地面处受轴向载荷Fy和径向载荷Fz等效为轮毂轴承中心的弯矩为M。
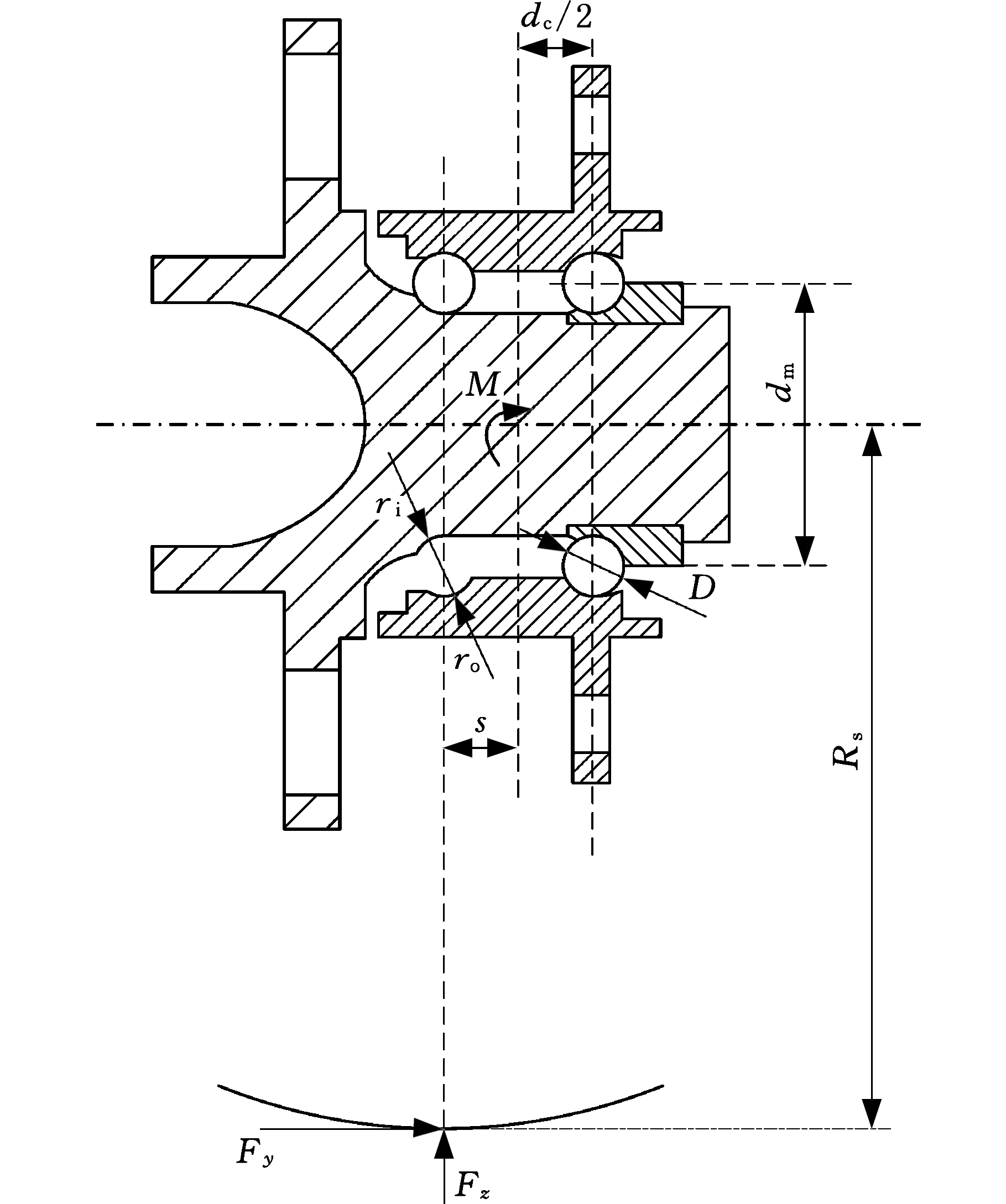
图1 轮毂轴承单元受力图
Fig.1 Force diagram of hub bearing unit
由轮毂轴承单元受力图(图1)可知:
M=Fzs-FyRs
(1)
式中,s为轮毂偏移量;Rs为轮胎半径。
载荷Fy和Fz由汽车满载时整车参数得到:
Fy=μFz
(2)
(3)
式中,μ为轮胎与路面间的附着系数;W为满载后轴重;g为重力加速度。
本文某车型的整车参数如表2所示。
表2 整车参数
Tab.2 Vehicle parameters
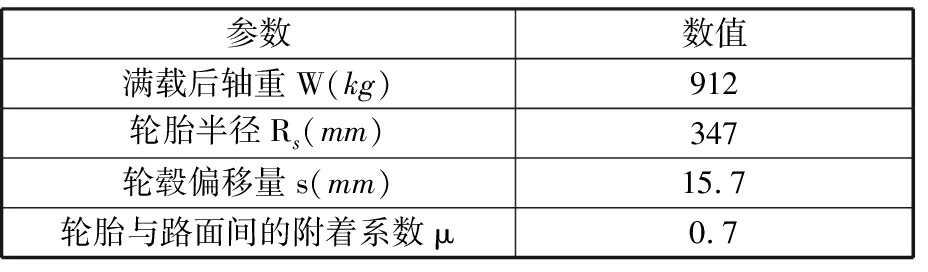
参数数值满载后轴重W(kg)912轮胎半径Rs(mm)347轮毂偏移量s(mm)15.7轮胎与路面间的附着系数μ0.7
1.2 第三代轮毂轴承载荷分布模型
对第三代轮毂轴承在弯矩作用下的接触状态进行分析,即接触变形、接触载荷和接触角的推导计算,得到轮毂轴承内部的载荷分布模型。
1.2.1 接触变形
在考虑滚道与滚动体接触变形时,一般认为实心轴和轴承座的刚性很好,轴承套圈不发生弯曲变形[10]。
当轮毂轴承受到弯矩后,滚动体与滚道之间会产生相对位移,接触角也会产生变化且各不相同。假设外法兰固定,内法兰旋转,左侧滚动体为第一列,右侧滚动体为第二列,最上端滚动体的位置角 ψ=0°,沿滚道依次增加。
图2为轮毂轴承受载后两列滚动体的位移示意图。当轮毂轴承受到弯矩时,δθa为倾角θ引起的内滚道曲率中心的轴向位移分量,δθr为倾角θ引起的径向位移分量,α0为初始接触角,α1、α2分别为内外列接触角,A为接触变形前内外滚道曲率半径中心距,δ1为第一列滚动体与滚道之间的总法向接触变形量。
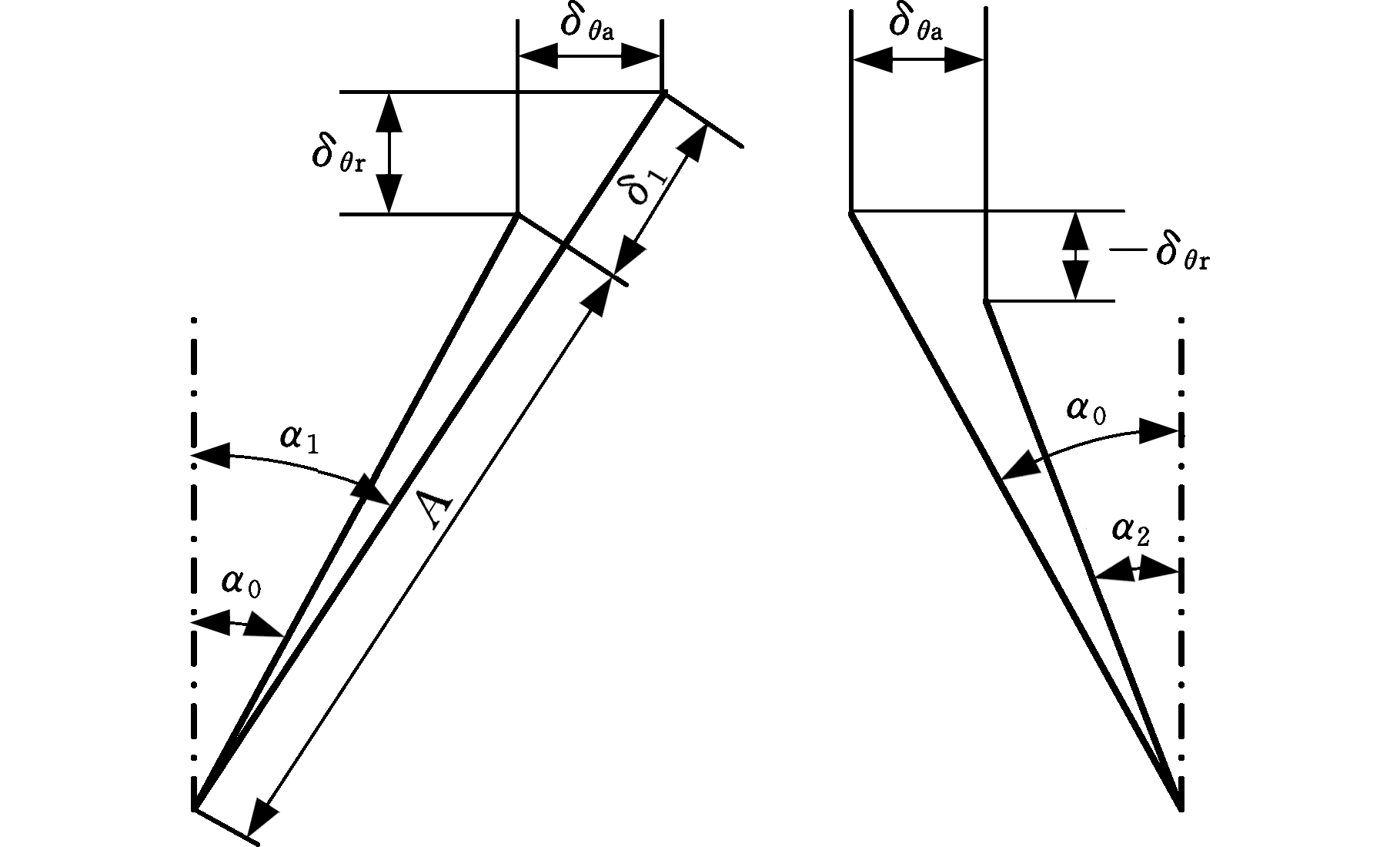
图2 位移前后两列滚道曲率中心的位移示意图
Fig.2 Diagram of the center of curvature of the two rows of raceways before and after the displacement
由图1和图2可以看出,当轮毂轴承受到弯矩时,由于两列滚动体的中心距为dc,则由倾角θ引起的滚动体径向位移分量可表示为
δθr=0.5dcθcosψ
(4)
同时,由倾角θ引起的滚动体轴向位移分量可以表示为
δθa=Riθcosψ
(5)
(6)
式中,Ri为内法兰两列内滚道的曲率中心轨迹的半径。
总的法向接近变形量是滚动体与内外法兰的接近量之和,也等于接触变形后内外滚道曲率半径中心距A′k与原始中心距A之差[10],因此有
δk=δki+δko=A′k-A
(7)
式中,下标i、o分别表示内法兰和外法兰;下标k=1,2,表示第一列或第二列滚动体组。
由图2所示的几何关系,第一列或第二列接触变形后的曲率半径中心距为
(8)
将式(4)、式(5)和式(8)代入式(7)可得轮毂轴承受弯矩作用后,两列滚动体在任意位置ψ处(ψ为滚动体在滚道内任意位置时的位置角),受载后与滚道任意位置的接触变形量为
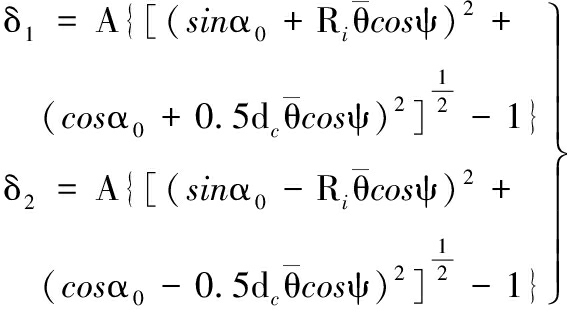
(9)
式中,![]() 为量纲一倾角,
为量纲一倾角,![]()
1.2.2 接触载荷和接触角
根据赫兹接触理论,法向接触载荷Q与法向接触变形量δ之间的关系为
Q=Kδn
(10)
(11)
式中,n=3/2(球轴承);K为载荷-位移系数[10] ;Ki、Ko分别为内外圈与滚动体接触的载荷-位移系数。
对于球轴承,Ki、Ko可由下式计算得到:
(12)
(13)
式中,ξ=i、o;∑ρξ为接触点的主曲率和函数; nξ为接触变形系数;η为两弹性体综合弹性系数。
(1)接触载荷。将式(9)代入式(10)得到任意位置角ψ处滚动体与滚道的法向接触载荷Qψk:
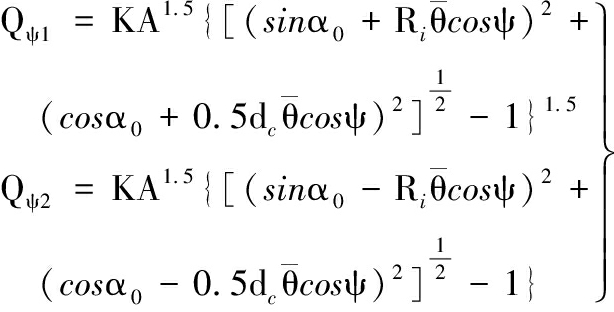
(14)
(2)接触角。轮毂轴承受载后,两列滚动体在任意位置角ψ处,实际接触角αψ1和αψ2由下式计算:
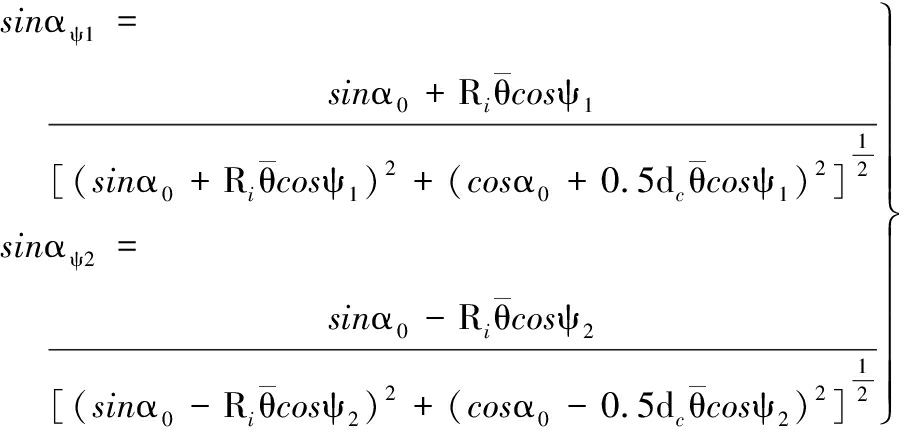
(15)
1.2.3 平衡方程的建立与求解
式(14)中的载荷Qψk可以分解为轴向载荷Qak与径向载荷Qrk:
Qak=Qψksinαψk
(16)
Qrk=Qψkcosψkcosαψk
(17)
轮毂轴承单元静力平衡图见图3,假设轮毂轴承受到的弯矩为M,对其进行受力分析并结合式(16)和式(17),得到静力平衡方程:
M=M1-M2=![]()
![]()
![]()
(18)
式中,M1、M2分别为两列滚动体受到的弯矩; ψ1、ψ2为两列滚动体的位置角。
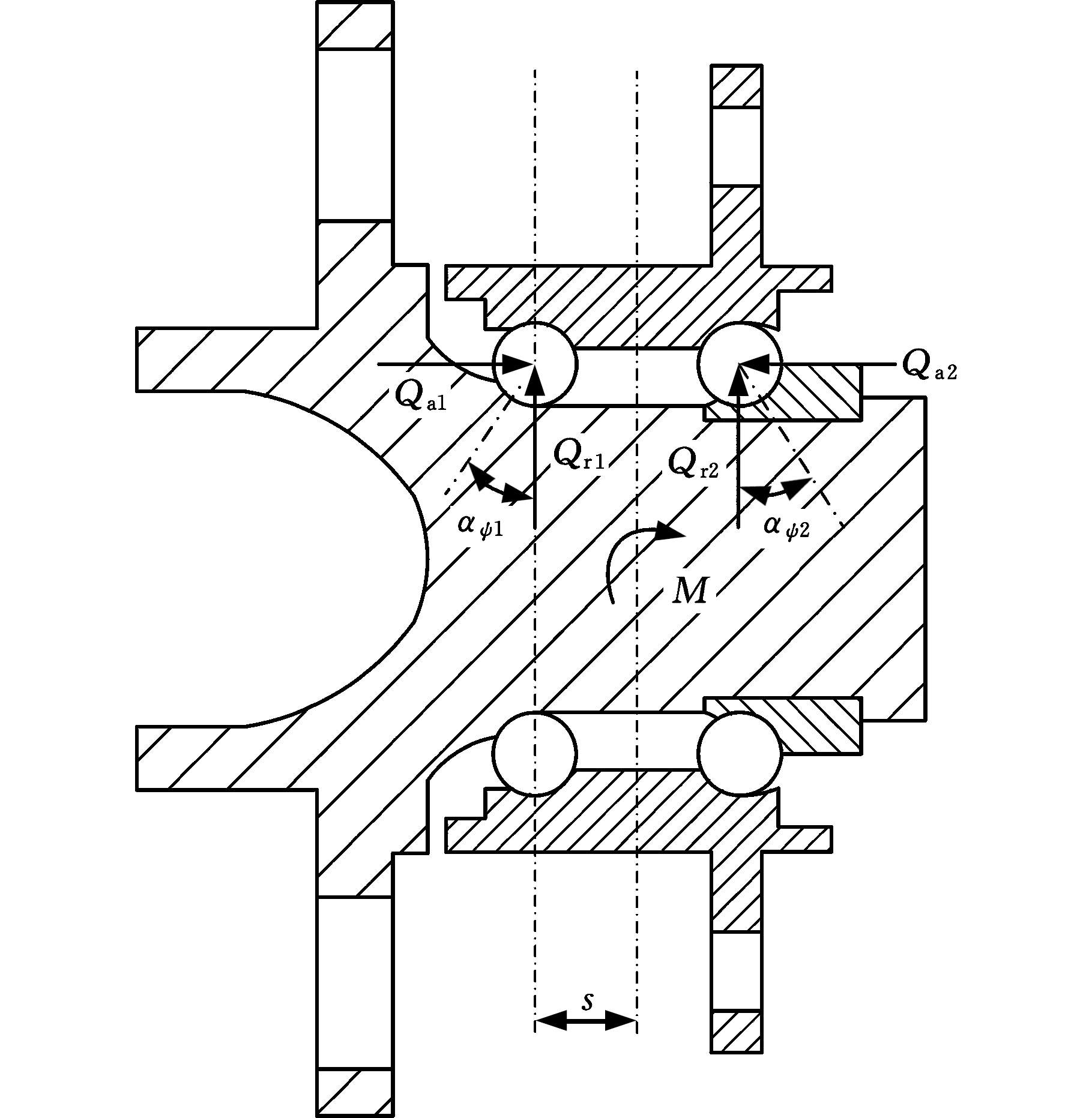
图3 轮毂轴承单元静力平衡图
Fig.3 Static balance diagram of hub bearing unit
本文采用Newton-Raphson迭代法,对非线性方程式(18)进行迭代求解,赋予角位移变量初值θ进行迭代,直到迭代误差小于0.000 001,停止迭代。然后,将计算得到的角位移代入式(14)和式(15)中,可以得到任意弯矩作用下的载荷分布,即每一列任意滚动体的接触载荷及接触角。
1.3 不同弯矩下轴承载荷分布结果与分析
滚动轴承的接触载荷和疲劳寿命是息息相关的,因此,需要对不同弯矩下轮毂轴承内部的两列载荷分布进行分析,尤其是滚动体与滚道的最大接触载荷。
对轮毂轴承施加不同弯矩M(8×105N·mm、1.2×106N·mm和1.6×106N·mm),研究弯矩的变化对接触载荷和接触角的影响。第三代轮毂轴承的两列滚动体个数均为13,且两列同序号的滚动体的位置角相差π/13。
(1)不同弯矩对接触载荷的影响。图4所示为施加不同弯矩作用时,两列滚动体的接触载荷随不同位置角的变化情况。可以看出:①两列滚动体的接触载荷在周向的变化趋势相反。第一列滚动体受载较小,第二列滚动体受载较大,第一列有7个滚动体受载,最大接触载荷出现在位置角ψ=0的滚动体处,第二列也有7个滚动体受载,而最大接触载荷出现在ψ=π的滚动体处。②不同弯矩对接触载荷在周向的影响规律具有一致性。弯矩越大,轴承内部两列载荷分布越不均匀,且弯矩对最大接触载荷的影响显著,弯矩越大,最大接触载荷也越大,对轮毂轴承寿命的影响就越大。
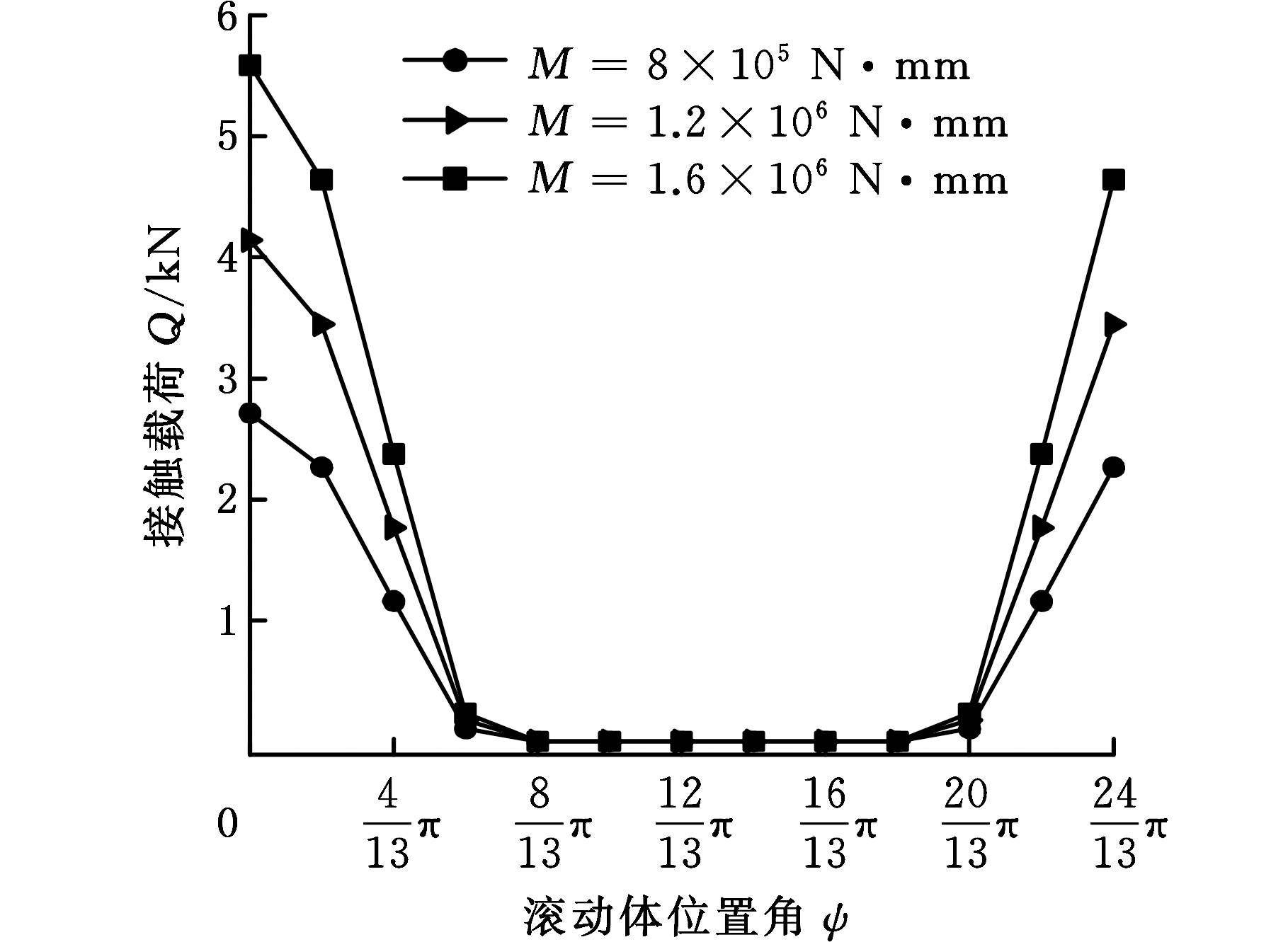
(a)第一列接触载荷变化
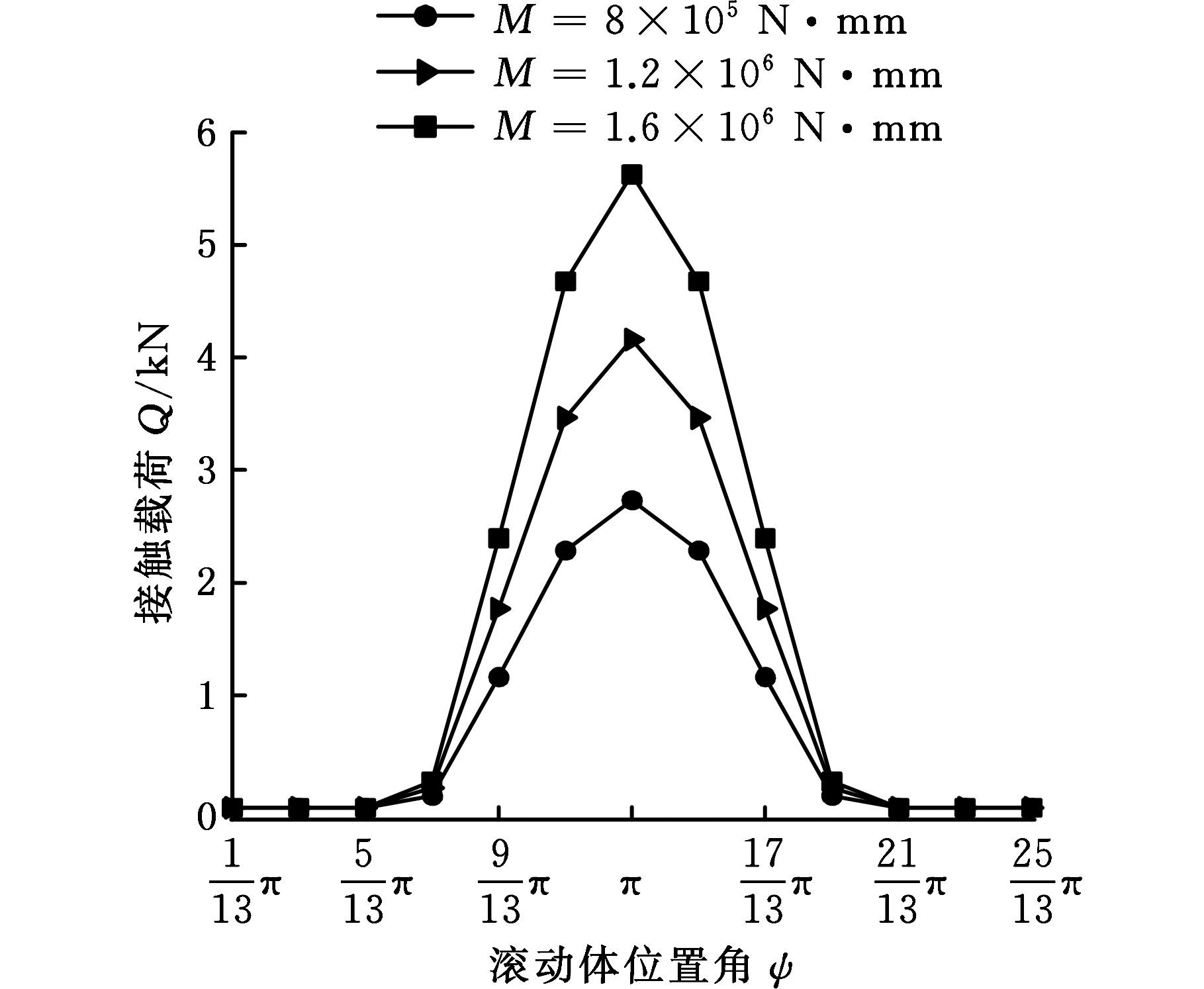
(b)第二列接触载荷变化
图4 不同弯矩下两列滚动体接触载荷
Fig.4 Contact load of two rows of rolling elements under different bending moments
(2)不同弯矩对接触角的影响。图5所示为施加不同弯矩时,两列滚动体的接触角随不同位置角的变化情况。可以看出:两列滚动体接触角在周向的变化趋势也相反。第一列接触角的最大值出现在ψ=0的滚动体处,最小值出现在ψ=12π/13和ψ=14π/13的滚动体处;第二列滚动体接触角变化与第一列趋势相反,最大值出现在ψ=π的滚动体处,最小值出现在ψ=π/13和ψ=25π/13的滚动体处;此外,弯矩越大,接触角的分布越不均匀。
2 轮毂轴承的疲劳寿命分析
滚动轴承接触疲劳不同于一般工程材料的结构疲劳,不能直接用Weibull理论来分析轴承的疲劳寿命[24],为此LUNDBERG等[4]于1947年提出了L-P滚动轴承疲劳寿命理论,该理论以滚道承载面下最大正交动态切应力作为滚道材料疲劳破坏的触发应力,用经验方法确定了下列关系,这一关系与他们的试验结果相当吻合,其基本方程为[4]
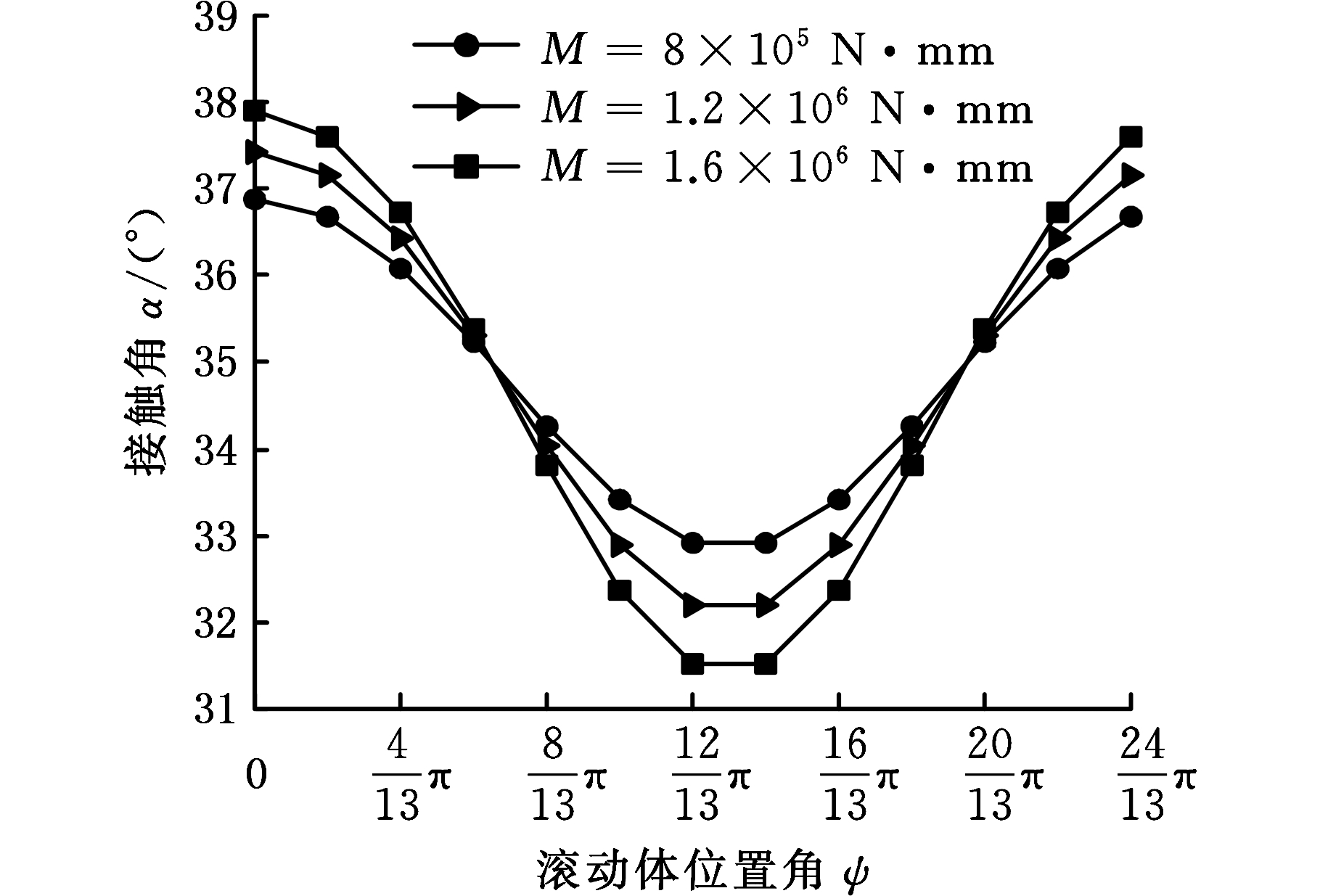
(a)第一列接触角变化
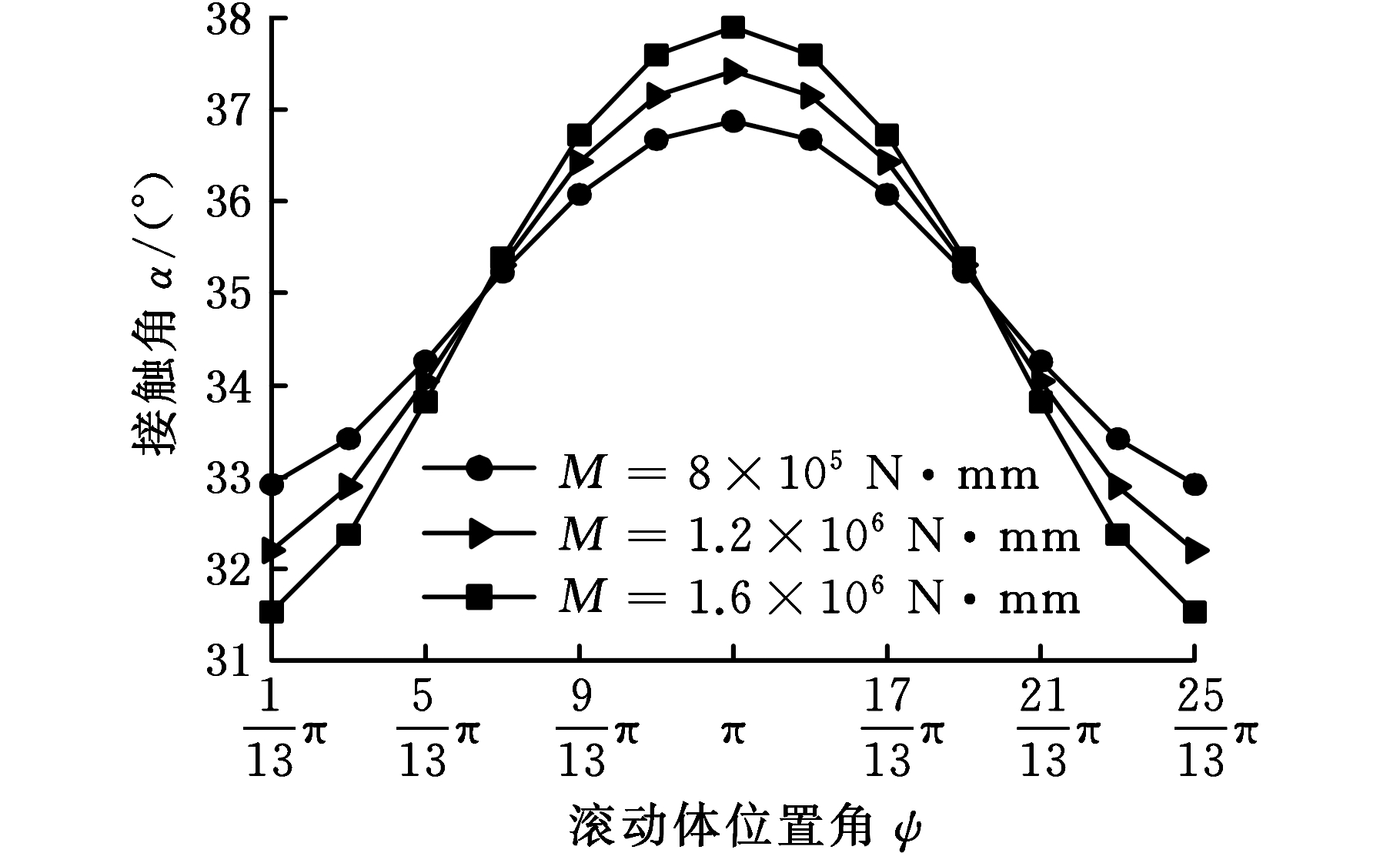
(b)第二列接触角变化
图5 不同弯矩下两列滚动体接触角
Fig.5 Contact angle of two rows of rolling elements under different bending moments
![]()
(19)
式中,τ0为最大正交切应力;z0为承载表面下τ0所在的位置;N为存活率为S时的应力循环次数;c、e、h为试验确定的常数;V为受应力体积。
最终推导出由额定接触载荷Qc与实际接触载荷Q表示的点接触疲劳寿命公式[25]:
(20)
对于点接触,有
![]() =3
=3
(21)
本文的轮毂轴承滚动体与滚道的接触疲劳寿命可由下式表示:
(22)
式中,L10为存活率为90%时,轴承的疲劳寿命公式(单位为106转),为了简化,下文以L代替L10。
2.1 L-P理论疲劳寿命模型
由载荷分布的分析可知,各个位置角上的滚动体接触载荷与接触角不同,且动态变化,因此,本文采用上述计算得到的是以每个滚动体与滚道接触处的接触载荷,而非滚动体组的等效载荷,来计算每个滚动体与滚道接触处的L-P理论疲劳寿命,再根据概率乘法定律进行统计处理得到整套轮毂轴承的寿命,该方法可更加准确地反映实际情况。
(1)滚道材料的接触疲劳寿命。根据式(22),滚动体与滚道接触处内外滚道材料的接触疲劳寿命为
(23)
(24)
式中,Qξ为滚道(滚动体)的实际动载荷;Qcξ为滚道基本额定动载荷[25];fξ为内外滚道曲率半径系数;γ为量纲一参数;α为接触角。
(2)滚动体材料的接触疲劳寿命。滚动体与滚道接触处滚动体的接触疲劳寿命计算公式为
(25)
(26)
式中,Q′cξ 为滚动体的基本额定动载荷[24];cξ为修正系数。
(3)整套轮毂轴承的疲劳寿命。轮毂轴承的整体疲劳寿命LS是对应于该轮毂轴承可靠度为S的寿命,整套轮毂轴承不破坏是各个组件(内外滚道接触材料和滚动体接触材料)不破坏这些事件之积,且各组件不破坏是相互独立的事件,根据概率乘法定律,整个系统的可靠度可由各组件的可靠度表示[10]:
S=S1×S2…Sn
(27)
根据二参数Weibull分布[26],对于特定载荷有
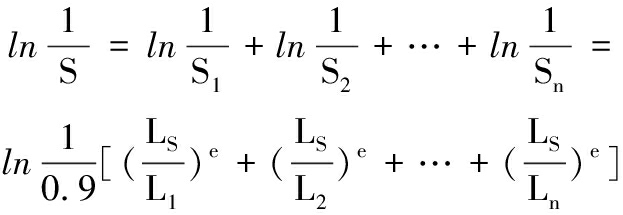
(28)
式中,L1、L2、…、Ln分别为各组件可靠度为90%时的疲劳寿命。
当系统可靠度S取90%时,系统寿命为
(29)
第三代轮毂轴承由两列滚动体与滚道组件构成,根据式(29),整套轮毂轴承的疲劳寿命为
(30)
式中,对于点接触轴承,指数![]()
每列组件的疲劳寿命由滚道材料组件和滚动体组件的疲劳寿命组成:
(31)
式中,Li、Lo分别为内外滚道材料寿命;LBi、LBo为接触处的滚动体材料寿命。
需要指出的是,式(31)中的Li、Lo可根据式(29)对不同位置角处滚道材料的接触疲劳寿命做统计处理得到:
(32)
滚动体在轴承运转中存在自转和公转,滚动体在计算寿命时是按照自转圈数来计算的,因此式(31)中滚动体的疲劳寿命LBi和LBo为
(33)
(34)
式中,T为轴承每转一周滚动体承受载荷的次数。
2.2 修正的L-P理论疲劳寿命模型
基于弹流润滑理论研究不同工况下润滑对轮毂轴承疲劳寿命的影响,不是对总的寿命修正系数AISO取一常数值,而是根据上述的载荷分布计算得到最小油膜厚度hmin和油膜参数λ,以此确定总的寿命修正系数AISO。这种方法考虑了轴承的最大载荷、油膜厚度等因素,更贴合实际情况,计算结果更精确。
本文基于ISO 281—2007标准提供的I-H理论系统法,对L-P模型计算的轴承疲劳寿命进行修正。综合考虑材料、污染、润滑及疲劳极限等因素对疲劳寿命的影响,计算公式为[8]
L=A1AISOLS
(35)
式中,A1为可靠度大于90%的可靠性系数,取1。
2.2.1 最小油膜厚度hmin
在滚动轴承中,滚动体与滚道接触区的润滑状态应按弹性流体动力润滑来考虑[22]。应用弹流润滑理论计算滚动体与滚道接触区的油膜厚度,不仅可以了解两表面之间的润滑状态,还可为轮毂轴承的分析计算提供必要的基础。
计算点接触弹流润滑膜厚最常用的是HAMROCK等[27]提出的量纲一油膜厚度计算方法,等温点接触弹流最小油膜厚度
(36)
式中,αL为黏度压力指数; η0为常压下的动力黏度; u为表面平均速度;E0为当量弹性模数;Qmax为受载最大的滚动体载荷;Rx为沿滚动体滚动方向的当量曲率半径;m为椭圆率。
不考虑滚动体打滑时,接触表面平均速度
(37)
式中,n为轴承转速,r/min。
椭圆率m可由下式计算:
(38)
(39)
式中,Ry为轴向平面内的当量半径;R为滚动体半径;rξ为内外圈的沟曲率半径。
当量弹性模数E0表示为
(40)
将式(37)~式(39)代入式(36),可以推导出滚动体与内外滚道的最小油膜厚度:
(41)
2.2.2 油膜参数λ
两表面间的润滑状态不仅取决于油膜厚度,还与表面粗糙度有关。油膜参数λ是衡量润滑效果的定量参数,综合了油膜厚度和粗糙度对润滑的共同影响[24]。当λ≥3时,为全膜弹流润滑;当λ<3时,为部分膜弹流润滑。滚动轴承中一般为混合润滑状态,λ≈2。
油膜参数λ的表达式为
(42)
s1=s2=1.25Ra
(43)
式中,s1、s2为两接触表面粗糙度的均方根值;Ra为表面粗糙度,本文Ra=0.05 μm。
2.2.3 总的寿命修正系数AISO
总的寿命修正系数AISO考虑了轮毂轴承材料、润滑、污染、疲劳极限应力以及轴承实际动载荷等多种因素的综合影响。本文主要研究润滑对寿命的影响,因此对润滑因素进行计算分析,其他因素值取定值。ISO 281—2007标准提供下式来计算总的寿命修正系数[18]:
(44)
κ=λ1.3
(45)
式中,CL为污染系数,按一般清洁标准取0.6;κ为润滑脂黏度比。
本文σlim=450 MPa;常数x1、x2和指数e1、e2、e3、e4为试验数据,具体取值如表3所示。
表3 式(44)中的常数和指数值
Tab.3 Constant and exponent values in equation(44)

油膜参数范围0.1≤λ<0.40.4≤λ<11≤λ<4x12.567 12.567 12.567 1x22.264 91.998 71.998 7e10.054 3810.190 870.071 739e20.830.830.83e31/31/31/3e4-9.3-9.3-9.3
2.3 寿命模型结果分析
根据经典L-P理论寿命模型,计算可靠度为90%时不同弯矩下的疲劳寿命值。同时,基于弹流润滑理论,根据载荷分布计算不同转速和弯矩下的寿命修正系数AISO,根据式(35)计算不同弯矩和转速下修正的L-P模型疲劳寿命值,研究不同弯矩和转速下润滑对轮毂轴承疲劳寿命的影响。
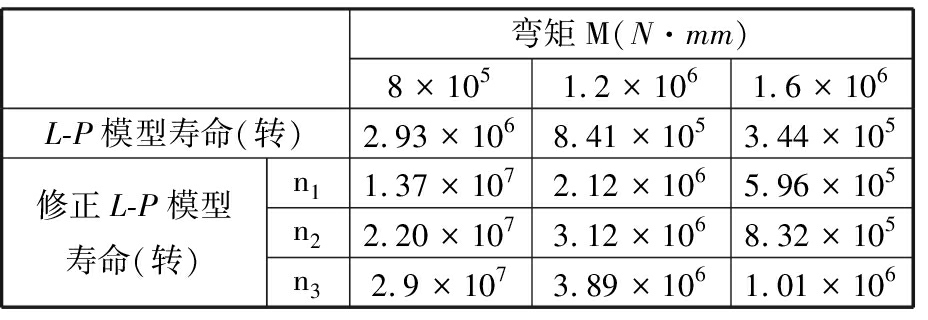
取汽车行驶速度为40 km/h、80 km/h和120 km/h时对应的轮毂轴承转速n1=306 r/min、n2=612 r/min和n3=917 r/min,根据提出的修正L-P模型计算得到疲劳寿命值,如表4所示。从表4中的数据可以看出:随着弯矩的减小,两种模型下的轮毂轴承寿命都增长。验证了弯矩大小对轮毂轴承寿命的影响规律。
表4 润滑修正前后的疲劳寿命对比
Tab.4 Comparison of fatigue life before and after
lubrication correction
弯矩M(N·mm)8×1051.2×1061.6×106L-P模型寿命(转)2.93×1068.41×1053.44×105修正L-P模型寿命(转)n11.37×1072.12×1065.96×105n22.20×1073.12×1068.32×105n32.9×1073.89×1061.01×106
另外,从表4中可以看出,由于修正的L-P模型充分考虑了润滑对疲劳寿命的影响,轮毂轴承的预测寿命显著增长,这与文献[25]中,滚动轴承良好的润滑状态可大幅度延长轴承寿命的结论相一致。同一弯矩作用下,随着转速的增加(汽车从低速到高速工况时),轮毂轴承寿命增长,这与文献[28]中转速提高有利于形成良好润滑状态,增长轴承寿命的结论一致;同一转速下,随着弯矩载荷的减小,轮毂轴承寿命也增长,且影响更加显著。
3 试验验证
本文采用图 6 所示的轮毂轴承旋转弯曲疲劳试验机测试第三代轮毂轴承的弯曲疲劳寿命。

图6 旋转弯曲疲劳试验机
Fig.6 Rotary bending fatigue test machine
3.1 旋转弯曲疲劳试验原理
本文中,旋转弯曲疲劳试验将第三代轮毂轴承的外圈固定,内圈通过适配器与施加弯矩的加载力臂相连,相当于弯矩施加在内圈,弯矩的方向不断变化,以此来模拟轮毂轴承在实际工况下的内圈旋转、弯矩方向不变的状态。
电机通过在不平衡质量块上方的软管带动不平衡质量块做圆周运动,形成离心力F,试验时,计算机需设定工作弯矩M,通过控制不平衡质量块的离心力F得
M=FL
(46)
试验终止的条件是:当旋转频率的变化量超过初始旋转频率f0的10%时系统自动判定轴承失效。该频率通过实验系统自动记录。
3.2 旋转弯曲疲劳试验方法
将轮毂轴承外圈固定、内圈安装在试验机加载力臂的适配器上,确认加载力臂长度L,设定加载弯矩M及循环次数,分别采用3套轮毂轴承进行试验。
(1)加载力臂应有足够的刚度,力臂长度L范围为 0.50~1.04 m(设定L= 0.685 m),加载系统精度控制在±2.5%以内。
(2)弯矩为
M=(μRs-s)FVt
(47)
式中, FV为额定负载, FV=Wg/2;t为强化系数,本文取t=1.8。
(3)加载循环次数设定为500 000 。
3.3 结果与对比
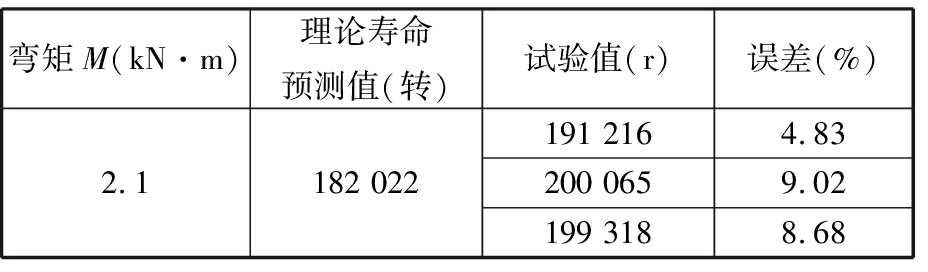
针对本文试验工况,利用所搭建的修正L-P理论寿命模型计算得到轮毂轴承寿命的预测值,并分别进行旋转弯曲疲劳试验,当测试系统测得的旋转频率超出允许范围时,试验件失效。轮毂轴承的理论模型预测值和试验值如表5所示。
表5 试验结果与理论模型结果的对比
Tab.5 Comparison of experimental results with
theoretical model results
弯矩M(kN·m)理论寿命预测值(转)试验值(r)误差(%)2.1182 022191 2164.83200 0659.02199 3188.68
由表5分析得,试验工况下的旋转弯曲疲劳寿命试验值与理论疲劳寿命预测值,误差均在10%以内,验证了本文基于载荷分布建立的修正理论疲劳寿命模型的正确性。
4 结论
(1)本文推导出的载荷分布模型可以弥补现有的寿命计算公式的不足,并给试验提供理论分析基础。
(2)基于建立的修正L-P模型可以看出,润滑对轮毂轴承疲劳寿命影响较大,转速越高影响越大,且弯矩越小,影响越显著。
(3)本文提出的修正L-P理论模型寿命预测值与试验值的误差均在10%以内,验证了本文基于载荷分布所建立的修正L-P理论疲劳寿命模型的正确性。
[1] 蒋兴奇, 黄志强. NSK第三代轮毂轴承的开发[J]. 轴承, 2005(4):46-49.
JIANG Xingqi, HUANG Zhiqiang. Development of NSK Third Generation Wheel Bearing[J]. Bearing, 2005(4):46-49.
[2] ZARETSKY E V. STLE Life Factors For Rolling Bearings, 2nd Edition[M]. Park Ridge: STLE Publication,1999.
[3] 冷钢. 复合工况下高速滚动轴承的寿命和可靠性预测[D]. 哈尔滨:哈尔滨工业大学, 2012.
LENG Gang . Prediction on Life and Reliability of High Speed Rolling Bearing in Complex Operating Conditions [D]. Harbin :Harbin Institute of Technology, 2012.
[4] LUNDBERG G,PALMGREN A.Dynamic Capacity of Rolling Bearings[J].Acta Polytechnica Mechanical Engineering Series,1952,2(4):96-127.
[5] GUPTA PRADEEP K,OSWALD F B,ZARETSKY E V. Comparison of Models for Ball Bearing Dynamic Capacity and Life[J]. Tribology Transactions, 2015,58(6):1039-1053.
[6] OSWALD F B, SAVAGE M, ZARETSKY E V. Space Shuttle Rudder/Speed Brake Actuator: a Case Study, Probabilistic Fatigue Life and Reliability Analysis[J]. Tribology Transactions, 2015, 58(1):186-196.
[7] PAULSON N R, EVANS N E, BOMIDI J A R, et al. A Finite Element Model for Rolling Contact Fatigue of Refurbished Bearings[J]. Tribology International, 2015, 85:1-9.
[8] 梁骁. 高速角接触陶瓷球轴承滚道接触载荷场分析[D]. 济南:山东大学, 2015.
LIANG Xiao. Contact Stress Field Analysis of Raceway of High-speed Angular Contact Ceramic Ball Bearings [D]. Jinan:Shandong University, 2015.
[9] International Organization for Standards. ISO 281—2007. Rolling Bearings-dynamic Load Ratings and Rating Life[S].Switzerland:ISO Copyright Office,2007.
[10] 邓四二,贾群义.滚动轴承设计原理[M].北京:中国标准出版社,2008.
DENG Sier, JIA Qunyi. Design Principle of Rolling Bearings [M]. Beijing: Standards Press of China, 2008.
[11] 徐鹤琴. 滚动轴承内部载荷序列分析与寿命计算[D]. 杭州:浙江大学, 2017.
XU Heqin. Sequence Analysis and Life Calculation of Internal Load of Rolling Bearing [D]. Hangzhou:Zhejiang University, 2017.
[12] WARDA B, CHUDZIK A. Effect of Ring Misalignment on the Fatigue Life of the Radial Cylindrical Roller Bearing[J]. International Journal of Mechanical Sciences, 2016, S111/112:1-11.
[13] SHAH D B, PATEL K M, TRIVEDI R D. Analyzing Hertzian Contact Stress Developed in a Double Row Spherical Roller Bearing and Its Effect on Fatigue Life[J]. Industrial Lubrication & Tribology, 2016(3): 361-368.
[14] LOSTADO R, MARTINEZ R F, DONALD B J M. Determination of the Contact Stresses in Double-row Tapered Roller Bearings Using the Finite Element Method, Experimental Analysis and Analytical Models[J]. Journal of Mechanical Science & Technology, 2015, 29(11): 4645-4656.
[15] XING Y, XU H, PEI S, et al. A Novel Non-Hertzian Contact Model of Spherical Roller Bearings[J]. Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology, 2016,230(1):3-13.
[16] XING Y, XU H, PEI S, et al. A New Method to Model Spherical Roller Bearings due to Self-aligning Feature[C]∥2015 International Mechanical Engineering Congress and Exposition. Houston, Texas: ASME, 2015: IMECE2015-50300, V009T12A005.
[17] TALLIAN T E. Simplified Contact Fatigue Life Prediction Model—Part Ⅱ:New model[J]. Journal of Tribology,1992,114(2):214-220.
[18] 赵联春,王东,晏丽明. 滚动轴承额定寿命计算中黏度比κ的分析及计算[J]. 轴承,2010(3):4-7.
ZHAO Lianchun, WANG Dong, YAN Liming. Analysis and Calculation of Viscosity Ratio Kappa in Bearing Rating Life Calculation [J]. Bearing, 2010 (3):4-7.
[19] MUTYALA K C, SINGH H, SAATCHI A, et al. Influence of DLC Coatings on the Oil-out, Debris and Fretting Wear Performance of Ball Bearings[C]∥STLE, 70th STLE Annual Meeting and Exhibition. Dallas, Texas, 2015.
[20] BALAN M R, TUFESCU A, CRETU S S. A Case Study on Relation Between Roughness, Lubrication and Fatigue Life of Rolling Bearings[J]. Materials Science and Engineering Conference Series, 2016, 147(1):012013.
[21] 唐洁. 基于弹流润滑理论的轮毂轴承力学性能及疲劳寿命研究[D]. 南京:南京航空航天大学, 2018.
TANG Jie. Research on the Mechanical Performance and Fatigue Life of Hub Bearing Based on the Theory of Elastohydrodynamic Lubrication[D]. Nanjing :Nanjing University of Aeronautics and Astronautics, 2018.
[22] HARRIS T A, KOTZALAS M N.滚动轴承分析(第二卷)[M].北京:机械工业出版社,2009.
HARRIS TA, KOTZALAS M N. Analysis of Rolling Bearings. Second Volume [M]. Beijing: China Machine Press, 2009.
[23] 杨超营. 复合载荷对轿车轮毂轴承单元疲劳寿命影响研究[D]. 杭州:浙江理工大学, 2015.
YANG Chaoying. Research on the Effect of Multi-load to the Fatigue of Life of Automotive Hub Bearing [D].Hangzhou: Zhejiang Sci-Tech University, 2015.
[24] WEIBULL W.A Statistical Theory of Strength of Materials[C]∥Proceedings of the Royal Swedish Institute for Engineering Research Stockholm. Stockholm, Sweden,1939.
[25] HARRIS TA, KOTZALAS M N.滚动轴承分析(第一卷)[M].北京:机械工业出版社,2009.
HARRIS TA, KOTZALAS M N. Analysis of Rolling Bearings. First Volume [M]. Beijing: China Machine Press, 2009.
[26] ZARETSKY E Y. Fatigue Criterion to System Design,Life,and Reliability[J]. Journal of Propulsion and Power,1987,3(1):76-83.
[27] HAMROCK B J, DOWSON D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part Ⅲ-Fully Flooded Results[J]. Tribology Transactions, 1975, 27(4):275-287.
[28] 邓磊, 于玫, 黎桂华, 等. 脂润滑轮毂轴承弹流润滑数值分析[J]. 润滑与密封, 2009, 34(10):21-25.
DENG Lei, YU Mei, LI Guihua, et al. Numerical Analysis of Elastohydrodynamic Lubrication of Grease Lubricated Hub Bearings [J]. Lubrication and Sealing, 2009, 34(10):21-25.
