0 引言
金属板料单点渐进成形(single point incremental forming, SPIF)是利用分层制造的思想,通过局部变形累积实现零件整体成形的一种新型板料柔性快速成形技术,无需模具或只需简易模具,适用于单件小批量、多样化和复杂形状产品的生产需求。然而,在SPIF技术中,过大的局部应力易引起过于集中的应变,致使板料易发生失稳、起皱、破裂等缺陷,尽管许多学者对SPIF工艺进行了广泛的理论与试验研究,然而在成形极限、成形效率、成形精度及表面质量等方面的不足始终制约着此项技术的工业化大范围应用,如何提高SPIF技术的成形极限、改善成形质量是该领域目前的研究热点。成形极限指的是金属板料在成形过程中介于应变安全区和应变破裂区的一个界限,由成形极限曲线(forming limit curve, FLC)进行表征,它位于主应变ε1、ε2所构建的平面坐标系内。为研究SPIF技术的成形极限,国内外学者进行了大量的工作,并取得了一定的成效[1-3]。
SOEIRO等[4]对SPIF过程中材料的应力应变进行了理论计算,他们认为板料在径向拉应力的作用下发生了破裂,且破裂会发生在与工具头接触的上边缘处。PARK等[5]提出了基于应变历史的极限状态判断方法,并对三种不同类型试样的应变历史和等效塑性应变进行了测量,研究结果表明,基于有效塑性应变的断裂成形极限图适用于预测先进高强度板料在复杂成形过程中的突然断裂。SIMONETTI等[6]提出了改进的应变数据拟合方法。陈劫实等[7]从能量的角度出发,基于总塑性功的积分形式,考虑了成形过程中应变路径变化、材料的硬化指数等因素的影响,建立了板料的成形极限判断依据。王进等[8]提出了通过渐进成形圆弧沟槽、十字交叉圆弧沟槽直至板料端部破裂后,测量破裂位置最大和最小主应变以获得板料渐进成形极限图的方法。王华毕等[9]通过数控机床渐进成形锥形零件,试验测量了不同因素(原始板厚、垂直增量步长、润滑剂种类、零件形状)下的成形极限角,以此来比较渐进成形性能以及探究限制材料成形极限的原因。
为提高板料在SPIF技术下的成形极限,部分学者尝试了双点渐进成形、双边渐进成形、电磁辅助渐进成形、激光辅助渐进成形、热渐进成形、增加支撑等复合工艺。SHAMSARI 等[10]采用液压胀形和SPIF相结合的方式提高成形极限和成形效率。ZHANG等[11]尝试将SPIF工件卸载后通过退火处理,以降低工件的回弹变形和提高成形极限。 JAWALE等[12]根据断裂力学的模式,通过试验确定了铜的断裂成形极限(FFL)和剪切裂缝成形极限(SFFL)。龚航等[13]对大型铝合金曲面件电磁渐进成形技术进行了研究。CUI等[14]采用电磁辅助SPIF和拉伸相结合的方式进行了大尺度薄壁椭圆体零件变形。李小强等[15]研究了整体加热和局部加热对成形极限的影响,试验发现随着温度的升高,材料的成形极限也会相应提高,局部加热的方式可使非加热区域的板料因处于相对低温而保持较好的刚性,从而提高了整体零件的精度。
综上所述,为避免成形缺陷并提高成形质量,国内外的科研工作者在板料成形极限的影响机理、研究手段、改善措施等方面做了诸多工作,并取得了大量的成果。本文以制件破裂区域的应变分布为研究对象,利用拓印法和显微观测法获取破裂区域的应变分布数据,选用插值法和多项式拟合法处理并分析应变数据,最终得到关于1060铝板在SPIF技术作用下的成形极限,实现了制件破裂的预测和控制。在此基础上,鉴于超声振动在塑性加工工艺中表现出来的提高成形极限、减小成形力等积极作用[16-18],本文将超声振动引入SPIF过程中以改变材料流变状态和组织演化机制来提高成形极限,通过试验对比研究了超声振动辅助渐进成形的FLC和传统渐进成形的FLC,验证并量化了超声振动对成形极限的改善效果。
1 数控单点渐进成形板料成形极限试验
由于板料成形极限源于试验,试验中的一些具体因素和标准不同,而这些因素和标准却对试验结果又有着重要的影响(如采用颈缩失效和破裂失效时,两者的判断标准不一样,试验中得到的FLC也不同),因此,本文基于板料SPIF的工艺要求,从试验条件的可观测性角度出发确定成形中的极限状态,以期提高成形试验结果的实用性和可靠性。
板料发生颈缩现象一般是材料细微组织的变化,实际生产中零件局部出现明显的颈缩痕迹即认为零件冲压失效,但由于板料在SPIF过程中的颈缩现象并不易观测[19-20],因此,1060铝板常温下的成形极限由板料的破裂极限来定义,当板料在成形过程中出现任何破损现象时即视为成形极限的判定标准。
1.1 试验原理和装置

图1 成形轨迹简图及试验装置
Fig.1 Forming trajectory diagram and test device
采用数控加工中心作为数控SPIF试验平台。通过预先编制好的数控程序控制成形工具头的运动轨迹,逐层成形出圆锥台成形工件。成形轨迹及装置如图1所示。试验系统由成形工具头、夹具和待成形板料组成,将1060铝板放在夹具底座上,板料四周用压板夹紧。成形工具采用圆柱形高速钢棒料球头状刀具,对刀具球头进行抛光处理。工具头直径为10 mm,原始板料厚度为1 mm,板料尺寸为140 mm×140 mm,并在板料表面印制圆形网格,最终成形圆锥台的成形壁角α=64°。成形过程中,层间距选择0.3 mm,工具头转速为750 r/min,进给速度为200 mm/min,润滑油选用昆仑L-HM46抗磨液压油。试验用1060铝板力学性能属性如表1所示。
表1 1060铝板的力学性能
Tab.1 Mechanics performance of 1060 Aluminum material

密度ρ(g/mm3)弹性模量E(GPa)泊松比μ屈服强度(MPa)2.69700.330厚度(mm)抗拉强度(MPa)规定非比例延伸强度σ0.2(MPa)断后伸长率(%)0.5~1.580~120606
1.2 成形极限的测量
网格测量是塑性变形实测中常用的一种测量方法,对板料极限应变的测量关键是确定极限状态,将破裂作为板料成形极限的判断依据。网格测量主要有三类方法:①直接测量法,将试件成形至破裂,测量破裂区域附近的网格,该方法操作简单但误差较大;②插值法,测量破裂失效变形网格附近的若干个网格,通过插值处理得出极限应变,该方法对初期网格数据测量要求较高,但插值结果比较准确;③与应变历程相关的测量方法[21-22],通过应变随时间的变化关系确定极限应变,该方法对设备精度要求较高,未能普遍使用。在研究过程中,本文利用拓印法将曲面变形问题转换成平面变形问题,结合现代数码显微技术进行精确测量,再采用插值和多项式拟合处理数据并绘制铝板的FLC。
数控SPIF试验中,最终成形工件多为曲面形状,其形变在毫米级。在金属板表面印刷网格,采取常用圆形网格形式,原始网格大小控制在直径2.2 mm。将胶带粘贴在被测曲面上,将成形曲面的网格形变拓印出来(即将制件空间曲面转换成平面),拓印出来的网格能够较为准确地反映出被测曲面网格的形变。采用ISM-PM200S数码显微镜配合USB数据传输采集测量系统来测量破裂区域的网格形变大小,如图2所示。

图2 拓印网格及测量设备
Fig.2 Rubbing grid and measuring equipment
1060铝板成形后圆形网格拉伸变形为椭圆形网格,分别测量每一个椭圆形网格的长短轴变化,将测量数据进行处理得到该板料的两个主应变。通过ISM-PM200S数码显微镜放大30倍后,依次测量出拓印的5条网格形变带,局部显示如图3所示,其中La为所测椭圆形网格的短轴,Lb为所测椭圆形网格的长轴,D为圆形网格(即La=Lb时的情况)直径。

(a) 第1、2、3条网格形变带(形变初段)

(b)第1、2、3条网格形变带(形变中段)

(c) 第4、5条网格形变带(形变初段)

(d) 第4、5条网格形变带(形变中段)
图3 放大30倍后网格形变
Fig.3 Mesh deformation after 30-fold magnification
1.3 测量与计算结果
每条网格形变带上分别有11个网格,测得的5条网格形变带的形变情况如表2所示。
板料受力后的应变情况主要有平面应变、胀形应变、拉伸应变,上述三种状态如图4所示,以SPIF圆锥件为研究对象,由表2中的数据可得,圆形网格成形后的形变为,椭圆形网格的长轴拉伸量较大,短轴伸长量较小。故此种成形应变状态可以看作平面应变状态。
表2 沿路径提取网格形变
Tab.2 Extract mesh deformation along
the prescribed path mm
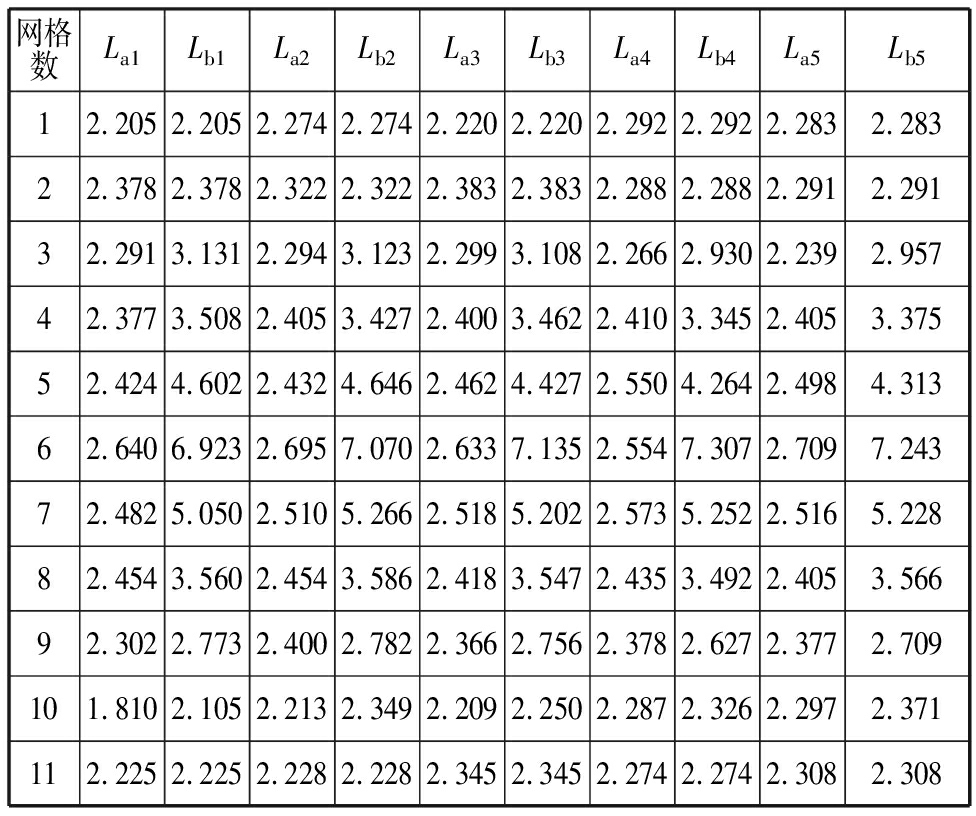
网格数La1Lb1La2Lb2La3Lb3La4Lb4La5Lb512.2052.2052.2742.2742.2202.2202.2922.2922.2832.28322.3782.3782.3222.3222.3832.3832.2882.2882.2912.29132.2913.1312.2943.1232.2993.1082.2662.9302.2392.95742.3773.5082.4053.4272.4003.4622.4103.3452.4053.37552.4244.6022.4324.6462.4624.4272.5504.2642.4984.31362.6406.9232.6957.0702.6337.1352.5547.3072.7097.24372.4825.0502.5105.2662.5185.2022.5735.2522.5165.22882.4543.5602.4543.5862.4183.5472.4353.4922.4053.56692.3022.7732.4002.7822.3662.7562.3782.6272.3772.709101.8102.1052.2132.3492.2092.2502.2872.3262.2972.371112.2252.2252.2282.2282.3452.3452.2742.2742.3082.308

(a)平面应变

(b)胀形应变

(c)拉伸应变
图4 三种应变状态
Fig.4 Three strain states
对于平面应变状态,板料成形中的厚向应力可以忽略不计,但厚向应变却不能忽略,因此板料的应变可以用三个主应变ε1、ε2和ε3来表示。根据体积不变定律,三个主应变之和为零,则三个应变变量之中的任何一个变量均可以由另外两个表示(即两个应变变量可以表示板料的应变状态)。由此,用面内的两个主应变ε1、ε2来表示铝板的应变状态,在成形后的板料上测量椭圆形网格的长短轴大小,就可计算得到板料的主次应变。主次应变的值可利用工程应变和真实应变两种计算方法,计算公式分别如下。
工程应变计算方法:
真实应变(对数应变)计算方法:
式中,D0为圆形网格变形前的原始直径,取D0=2.2 mm。
由于工程应变需计算无穷多个中间状态的工程应变,其总变形量为近似每个中间量之和,不能准确反映出材料的实际变形情况,而真实应变则反映了板料变形的实际情况,故在本试验研究中,采用真实应变进行计算。用ε1表示计算得到的轴向网格应变,ε2表示计算得到的切向网格应变;将成形后板料的轴向网格应变作为第一主应变,切向网格应变作为第二主应变。计算可得到5条网格形变带的应变,如表3所示。
表3 成形后的板料沿路径提取网格应变
Tab.3 The grid strain data along the path after
forming the sheet metal
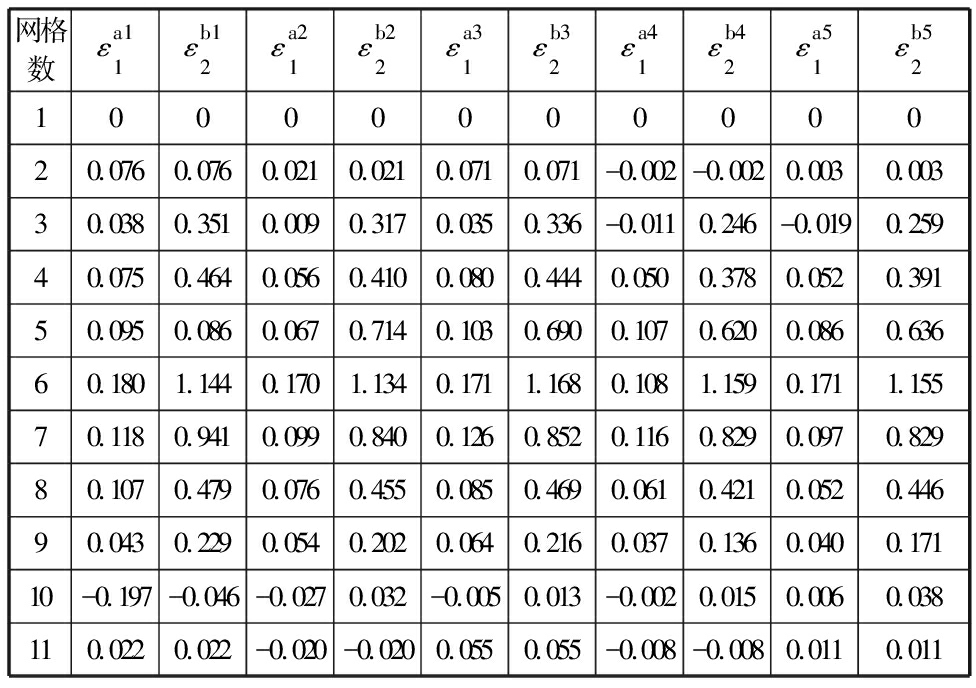
网格数εa11εb12εa21εb22εa31εb32εa41εb42εa51εb521000000000020.0760.0760.0210.0210.0710.071-0.002-0.0020.0030.00330.0380.3510.0090.3170.0350.336-0.0110.246-0.0190.25940.0750.4640.0560.4100.0800.4440.0500.3780.0520.39150.0950.0860.0670.7140.1030.6900.1070.6200.0860.63660.1801.1440.1701.1340.1711.1680.1081.1590.1711.15570.1180.9410.0990.8400.1260.8520.1160.8290.0970.82980.1070.4790.0760.4550.0850.4690.0610.4210.0520.44690.0430.2290.0540.2020.0640.2160.0370.1360.0400.17110-0.197-0.046-0.0270.032-0.0050.013-0.0020.0150.0060.038110.0220.022-0.020-0.0200.0550.055-0.008-0.0080.0110.011
2 1060铝板成形极限曲线的绘制
测量数据具有离散性与跳跃性,测量过程中存在人为的误差,采用在区间上的数值插值能有效地减少数据之间的跳跃,可去除与插值曲线相差比较大的数据点。三次样条插值函数具有平滑可导性、准确性高的优点,因此本文采用数值分析中常用的三次样条插值。
利用MATLAB对所测数据进行插值拟合,编写插值三次样条插值程序,采用三次样条插值函数spline(X0,Y,x)。初值X0为成形后经过破裂区域的网格编号1~11,Y1~Y5分别为测量5条形变带长短轴的实际形变,插值步长x为0.05。将成形后椭圆形网格的短轴形变量La记为轴向网格形变量,长轴形变量Lb记为切向网格形变,得到的轴向和切向插值的曲线分别见图5、图6。

图5 轴向网格形变插值曲线
Fig.5 Interpolation curve fitting deformation of axial mesh

图6 切向网格形变插值曲线
Fig.6 Interpolation curve fitting deformation of tangential mesh
从被测的5条形变带数据的插值曲线可以看出,轴向网格形变插值曲线较为分散,切向网格形变插值曲线重合度高。若要提取破裂区周围的最大形变量来绘制FLC,则轴向形变插值曲线的数据分散、误差较大,而切向网格形变插值曲线在最大形变(破裂区)附近的数据重合度高,误差较小。
由于5条轴向插值曲线重合度不高,若要采用其数据绘制FLC则误差较大,故需要从数据整体变化趋势的角度,并结合数据分布的大致情况来确定应用的拟合模型,采用多项式曲线拟合形变以减小其误差。对所测数据进行多项式拟合,同样将成形后椭圆形网格的短轴形变量La记为轴向网格形变量,长轴形变量Lb记为切向网格形变量,其中以第2条网格形变带轴向、第3条网格形变带切向拟合的多项式曲线为例,分别见图7、图8。

(a) 多项式拟合曲线

(b) 残差
图7 轴向网格多项式拟合曲线及其对应残差
Fig.7 Curvilinear polynomial fitting axial mesh and its corresponding residuals

(a) 多项式拟合曲线

(b) 残差
图8 切向网格多项式拟合曲线及其对应残差
Fig.8 Curvilinear polynomial fitting tangential mesh and its corresponding residuals
图7a中的离散数据点为实际测得的轴向网格形变量,分别用三次多项式和五次多项式曲线拟合实测的数据。图7b为对应残差,其中三次多项式的残差模为0.188 58 mm, 五次多项式的残差模为0.174 46 mm。由表2可知,第2条网格形变带的轴向最大网格形变为2.695 mm,则可计算出轴向最大网格形变的相对误差如下。
三次多项式拟合相对误差为
五次多项式拟合相对误差为
图8a中的离散数据点为实际测得的切向网格形变量,分别用三次多项式和七次多项式曲线拟合实测的数据。图8b为对应残差,其中三次多项式的残差模为3.212 7 mm, 七次多项式的残差模为1.634 2 mm。由表2可知,第3条网格形变带的切向最大网格形变为7.135 mm,则可计算出切向最大网格形变的相对误差如下:
三次多项式拟合相对误差为
七次多项式拟合相对误差为
由网格形变多项式拟合曲线可以发现,轴向多项式拟合曲线的最大相对误差为6.997%,误差较小,且三次拟合与五次拟合的相对误差变化不大。由此可知,轴向五次多项式拟合曲线就能很好地反映出实际测得的形变量曲线。由于在SPIF过程中制件深度方向的形变要远大于侧面曲面的形变,出现的拉伸破损为切向拉伸破损,所以切向的应变变化大,且切向多项式拟合曲线的误差较大,最大相对误差为45.03%。三次多项式与七次多项式的相对误差变化也很大,故切向多项式拟合曲线并不能真实反映出实测数据的变化情况。其他各条网格形变带在轴向和切向拟合的多项式均符合上述类似的多项式拟合结果。
经上述分析,最终提取轴向五次多项式拟合曲线数据和切向三次样条插值曲线数据来绘制1060铝板的FLC。在成形后的网格形变带上,被测量的网格在第5个网格上没有发生破损失效,而在第6个网格上发生了破损失效。若将第5个网格作为应变的极限,则有可能实际还没有达到最大应变;若将第6个网格作为应变的极限,但第6个网格已经发生了破损失效,且由于破裂区域实际测量中应变明显会增大,故也不能作为极限应变,如图9所示。由此,采取从轴向形变曲线拟合五次多项式中求取第5~6个网格的区间数据,作为成形极限应变来绘制FLC;从切向三次样条插值曲线中提取从第5~6个网格的连续数据,作为成形极限应变来绘制FLC。

(a) 测量破裂区域

(b) 实际破裂区域
图9 测量破裂区域与实际破裂区域的对比
Fig.9 Comparison between the measured crevasse and the actual crevasse
将成形后椭圆形网格的短轴应变作为平面第一主应变ε1,长轴应变作为平面第二主应变ε2。得到的破裂区网格5、6的极限形变量所对应的应变如图10所示。最终将第一主应变ε1作为横坐标,第二主应变ε2作为纵坐标,绘制得到1060铝板的FLC,如图11所示。可以看出,FLC将整个区域分为安全区与破裂区,在FLC以下时认为板料的变形是安全的,在FLC以上时认为板料发生破裂或者失稳。

(a) 第一主应变

(b) 第二主应变
图10 主应变曲线
Fig.10 Principal strain curve

图11 1060铝板成形极限曲线
Fig.11 Forming limit curve of 1060 aluminum sheet
如图12所示,将直接测量的离散点与拟合曲线进行对比,离散的数据点为直接测量法所得成形破裂区网格的应变极限,曲线为数据拟合的应变极限曲线。由于直接测量法是通过测量破损区域附近有限数量个网格,且均为已出现了破裂的网格或是形变量还未达到破裂的网格,故存在不可避免的测量误差。已破裂网格的应变比极限网格的应变要大,而未破裂的网格则很难判断刚好达到应变极限。所以直接测量得到的应变极限较为分散,安全区和破裂区的界限不易区分出来,从实际的成形结果分析,若要得到最大形变的成形件,则并不能作为良好的依据。拟合得到的曲线连续而光滑,应变数据点比破裂点低,同时比未破裂点高,更符合实际情况。在安全系数要求较高的板料成形中,应用拟合得到的FLC更为安全可靠。

图12 直接测量法与拟合的对比
Fig.12 Comparison of direct measurement and interpolation
3 超声振动对成形极限曲线的改善
在前述的常温静态试验研究的基础上,本文进一步针对不同功率和频率超声振动下的1060铝板的SPIF性能进行了对比试验研究,采用表4中的5种功率和频率数据,以成形力为监测指标,分析了超声振动功率和频率对铝板成形性能的影响。
表4 超声波振动参数数据
Tab.4 Data of ultrasound vibration parameters

序号频率(kHz)功率(W)序号频率(kHz)功率(W)11580430140220100535160325120
依据本课题组前期的研究成果[23],当频率一定时,随着功率从80~ 120 W的增大,成形力呈减小趋势,之后随着功率从120~160 W的继续增大,成形力又呈现增大的趋势,当功率为120 W时,成形力最小;而当功率一定时,随着超声振动频率从15 ~25 kHz的提高,板料的成形力逐渐减小,当频率从25~35 kHz继续提高,其成形力又逐渐增大,当频率为25 kHz时,成形力最小。由此可知,当频率为25 kHz、功率为120 W时,1060铝板的成形效果最好。
利用静态SPIF技术成形一圆锥台件直至发生破损,同时利用超声波参数为频率25 kHz、功率120 W的数控SPIF技术使同一圆锥台件发生破损,并将两者破裂时的应变极限曲线进行了对比,以说明超声振动对SPIF极限的影响。试验和分析所得静态以及外加超声振动后的板料成形极限应变的对比如图13所示。
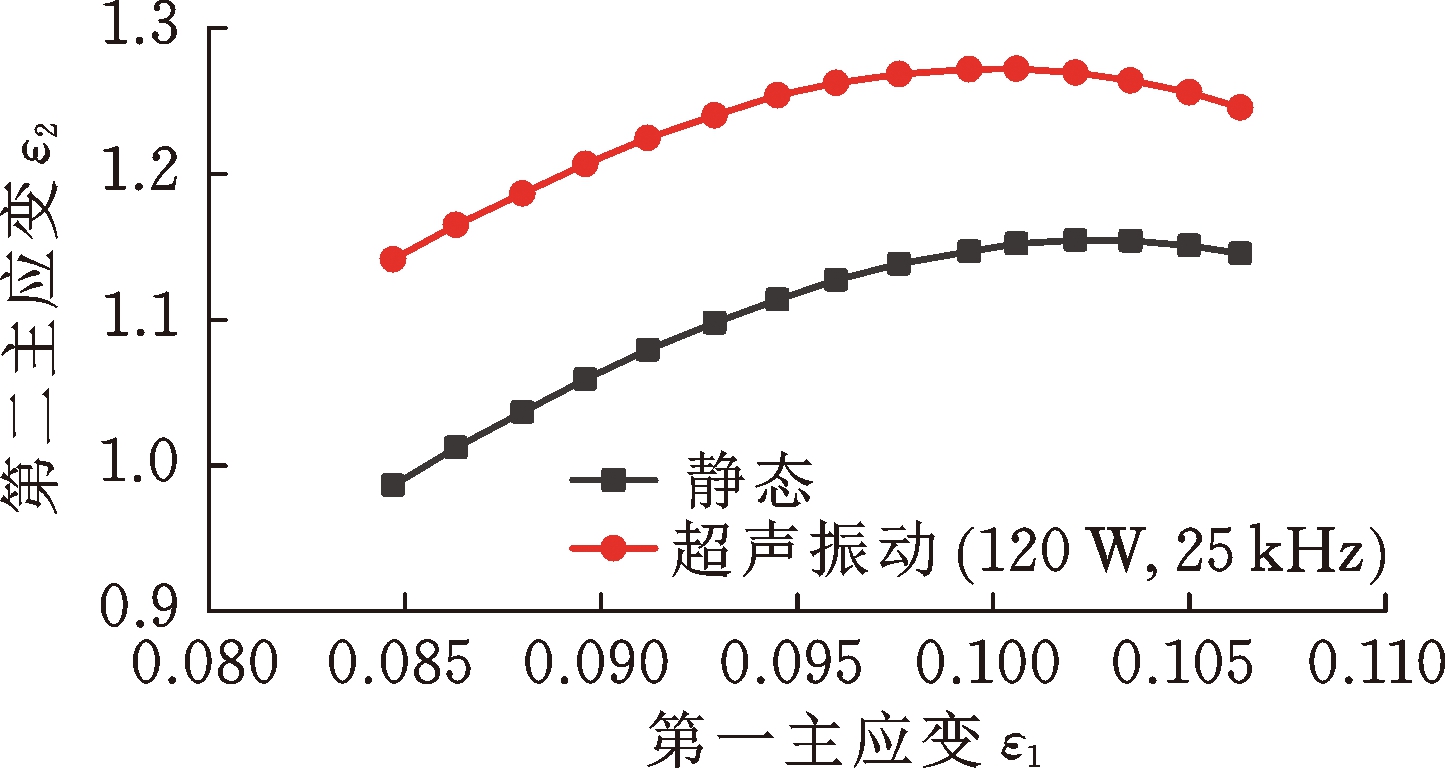
图13 静态与超声极限应变对比
Fig.13 Comparison of static and ultrasound limit strain
从图13中可以看出,在理想振型参数的作用下,1060铝板超声数控SPIF的塑性应变极限较静态条件下有所提高,提高幅度在11%左右。在该振动功率下,由于超声能量的输入,促进了铝板位错运动,对铝薄板滑移系开动有影响,使塑性变形更易进行,因此,铝板的屈服强度有所降低。当超声振动的能量刚好能对滑移系有促进作用时,薄铝板的应变极限就会有一定程度的提高。
4 结论
(1)1060铝板在单点渐进成形(SPIF)技术作用下的形变量处于毫米级,且成形制件为空间曲面件,因此采用拓印法能够将空间变形问题转化成可测的平面变形问题,并利用ISM-PM200S数码显微镜测量破裂区域的拓印带以获取制件的成形极限。经实践证实,该方法具有一定的可行性和实用性。
(2)因直接测量的离散数据存在不可避免的测量误差,故本文提出了基于插值曲线和多项式拟合的数据优化处理方法。对拟合优化后的1060铝板成形极限曲线(FLC)进行了分析,得到了该材料制件在SPIF技术下的破裂区和安全区以及制件破裂区域的应变分布,实现了制件破裂的预测和控制。
(3)为进一步提高1060铝板的成形极限,将超声波振动赋予到成形工具头上,以改善材料的流变机理和组织演化机制。通过试验对比研究了超声振动辅助下与传统渐进成形下的FLC,试验结果表明,当频率为25 kHz、功率为120 W时,1060铝板料制件的成形极限得到了明显的提高。
[1] 曹宇, 高锦张, 贾俐俐. 渐进成形圆孔翻边变形区厚度减薄现象的模拟研究[J]. 锻压技术, 2015, 40(2):52-59.
CAO Yu, GAO Jinzhang, JIA Lili. Numerical Simulation for Thickness Thinning of Deformation Zone on Hole-flanging by Incremental Forming[J]. Forging & Stamping Technology, 2015,40(2):52-59.
[2] ANDRADE R, SKURTYS O, OSORIO F. Development of a New Method to Predict the Maximum Spread Factor for Shear Thinning Drops[J]. Journal of Food Engineering, 2015, 157:70-76.
[3] MORALES-PALMA D, VALLELLANO C, GARC A-LOMAS F J. Assessment of the Effect of the Through-thickness Strain/Stress Gradient on the Formability of Stretch-bend Metal Sheets[J]. Materials & Design, 2013, 50(17):798-809.
A-LOMAS F J. Assessment of the Effect of the Through-thickness Strain/Stress Gradient on the Formability of Stretch-bend Metal Sheets[J]. Materials & Design, 2013, 50(17):798-809.
[4] SOEIRO J M C, SILVA C M A, SILVA M B, et al. Revisiting the Formability Limits by Fracture in Sheet Metal Forming[J]. Journal of Materials Processing Technology, 2015, 217:184-192.
[5] PARK N, HUH H, LIM S J, et al. Facture-based Forming Limit Criteria for Anisotropic Materials in Sheet Metal Forming[J]. International Journal of Plasticity, 2017,96:1-35.
[6] SIMONETTI O P, RAMAN S V. Straining to Justify Strain Measurement[J]. Jacc-cardiovascular Imaging, 2010, 3(2):152-154.
[7] 陈劫实, 周贤宾. 板料成形极限预测新判据[J]. 机械工程学报, 2009, 45(4):64-69.
CHEN Jieshi, ZHOU Xianbin. New Forming Limit Prediction Criterion for Sheet Metals[J].Journal of Mechanical Engineering,2009,45(4):64-69.
[8] 王进,姜虎森,陶龙,等.板料渐进成形极限图测试方法研究[J].锻压技术,2013,38(2):34-36.
WANG Jin, JIANG Husen, TAO Long, et al. Study on Experimental Method of Measuring Forming Limit Diagram in Incremental Sheet Forming[J]. Forging & Stamping Technology, 2013,38(2):34-36.
[9] 王华毕,桑文刚,魏目青.金属板料单点渐进成形性能的研究[J].机械设计与制造,2017(1):108-111.
WANG Huabi, SANG Wengang, WEI Muqing.Research of Sheet Metal Based on Single Point Incremental Formability[J].Machinery Design & Manufacture, 2017(1):108-111.
[10] SHAMSARI M, MIRNIA M J, ELYASI M, et al. Formability Improvement in Single Point Incremental Forming of Truncated Cone Using a Two-stage Hybrid Deformation Strategy[J]. International Journal of Advanced Manufacturing Technology, 2017, 9:1-12.
[11] ZHANG Z, ZHANG H, SHI Y, et al. Springback Reduction by Annealing for Incremental Sheet Forming[J]. Procedia Manufacturing, 2016, 5:696-706.
[12] JAWALE K, DUARTE J F, REIS A, et al. Characterizing Fracture Forming Limit and Shear Fracture Rorming Limit for Sheet Metals[J]. Journal of Materials Processing Technology, 2018, 255:886-897.
[13] 龚航,黄亮,李建军,等.大型铝合金曲面件在电磁渐进成形首次放电条件下的起皱行为研究[J].中国材料进展,2016, 35(4):284-291.
GONG Hang, HUANG Liang, LI Jianjun, et al. Research on Wrinkling Behavior of Large Aluminium Alloy Curved Parts under the Condition of First Discharge of Electromagnetic Progressive Forming[J]. Chinese Material Progress, 2016, 35(4):284-291.
[14] CUI Xiaohui, MO Jianhua, LI Jianjun, et al. Large-scale Sheet Deformation Process by Electromagnetic Incremental Forming Combined with Stretch Forming[J]. Journal of Materials Processing Technology, 2016, 237:139-154.
[15] 李小强,董红瑞,张永生,等.板材数控热渐进成形工艺研究进展[J].塑性工程学报,2018,25(5):87-98.
LI Xiaoqiang, DONG Hongrui, ZHANG Yongsheng, et al. Review of Hot Incremental Sheet Forming Process[J]. Journal of Plasticity Engineering, 2018,25(5):87-98.
[16] 赵升吨,李泳峄,范淑琴.超声振动塑性加工技术的现状分析[J].中国机械工程,2013,24(6):835-840.
ZHAO Shengdun, LI Yongyi, FAN Shuqin. Analysis of Present Situation of Ultrasonic Vibration Plasticity Machining Technology[J]. China Mechanical Engineering, 2013, 24(6):835-840.
[17] 柏朗,李言,杨明顺,等.超声振动-单点增量复合成形过程中成形力的分析与建模[J].机械工程学报,2019,55(2):42-50.
BAI Lang, LI Yan, YANG Mingshun, et al.Analytical Model of Ultrasonic Vibration Single Point Incremental Forming Force[J].Journal of Mechanical Engineering, 2019,55(2):42-50.
[18] LANGENECKER B. Effects of Ultrasound on Deformation Characteristics of Metals[J]. IEEE Transactions on Sonics &Ultrasonics, 1966, 13(1):1-8.
[19] ANDRADE R, SKURTYS O, OSORIO F. Development of a New Method to Predict the Maximum Spread Factor for Shear Thinning Drops[J]. Journal of Food Engineering, 2015, 157:70-76.
[20] 祁爽,蔡力勋,包陈,等.基于应力三轴度的材料颈缩和破断行为分析[J].机械强度, 2015,37(6):1152-1158.
QI Shuang, CAI Lixun, BAO Chen, et al. Study on Necking and Fracture of Ductile Materials Based on Stress Triaxiality[J]. Journal of Mechanical Strength,2015,37(6):1152-1158.
[21] SOTO G, FONTBONA J, CORTEZ R, et al. An Online Two-stage Adaptive Algorithm for Strain Profile Estimation from Noisy and Abruptly Changing BOTDR Data and Application to Underground Mines[J]. Measurement, 2016, 92:340-351.
[22] GUAN W S, HUANG H X. A Proposed Technique to Acquire Cavity Pressure Using a Surface Strain Sensor during Injection-compression Molding[J]. Journal of Manufacturing Science & Engineering, 2013, 135(2):021003.
[23] 柏朗,李言,杨明顺,等.超声振动单点增量成形力研究[J].机械科学与技术,2018,37(2):270-275.
BAI Lang, LI Yan ,YANG Mingshun, et al. Research on Forming Force in Single Point Incremental Forming with Ultrasonic Vibration[J].Mechanical Science and Technology for Aerospace Engineering, 2018,37(2):270-275.
