0 引言
波纹夹芯结构具有质轻、隔热与降噪性能好、比强度和比刚度高等优点,并且其开放式的单胞设计使其拥有良好的流通性能和散热性能,因此,波纹夹芯结构在航空航天、高速列车、汽车、舰船等领域应用广泛,其抗冲击特性受到了冲击工程领域众多学者的关注。ZHANG等[1]对激光焊接三角形波纹夹芯板和单层板进行了空爆实验研究,并通过有限元模拟揭示了靶板的动态响应过程和破坏机理,研究结果表明,低脉冲水平下夹芯板背面板挠度低于单层板背面板挠度,而高脉冲水平下夹芯板更容易发生断裂,并且增加前面板厚度能够有效提高夹芯板的抗爆炸性能。任鹏等[2]通过实验与数值模拟相结合的方法研究了三角形波纹夹芯板在水下爆炸冲击载荷下的动态响应特性和防护性能,并与相同面密度格栅夹芯板以及单层板进行了对比,研究结果表明,三角形波纹夹芯板抗冲击性能高于单层板和格栅夹芯板的抗冲击性能。RIMOLI等[3]采用实验和数值模拟相结合的方法研究了湿砂冲击载荷下,铝合金三角形波纹夹芯板和等面密度单层板的力学响应特性,研究结果表明,将夹芯板的芯体质量分配到背面板有助于减小靶板的挠度,并且波纹夹芯板的最大永久挠度低于单层板的最大永久挠度。PANIGRAHI等[4]通过数值模拟研究了泡沫填充三角形铝合金波纹夹芯板对弹体的抗冲击性能,发现填充聚氨基甲酸酯(PU)、聚甲基丙烯酰亚胺泡(PMI)和聚氯乙烯(PVC)泡沫的夹芯板抗冲击性能差异较小,但是,填充金属泡沫的夹芯板抗冲击性能高于填充聚合物泡沫的抗冲击性能。HOLMEN等[5]对无填充与填充砂的三角形6005-T6铝合金波纹夹芯板,在卵形头弹体冲击下的穿孔阻力进行了实验和数值模拟研究,发现填充砂的波纹夹芯板的抗弹性能明显高于无填充结构的抗弹性能。周昊等[6]和邓泽华等[7]分别对树脂填充铝合金三角形波纹夹芯结构和梯度波纹夹层结构,在空间碎片超高速撞击下的动态响应特性进行了数值研究,研究结果表明,两种结构的防护性能均优于相同面密度的Whipple结构。
从文献分析可以发现,国内外对三角形波纹夹芯板的冲击响应特性进行的一些研究多集中于爆炸冲击领域,而关于该结构弹道冲击损伤特性的研究相对比较少。本文建立平头弹体冲击三角形波纹夹芯板与等面密度单层板的有限元模型,然后对比分析几何结构对其防护性能以及损伤特性的影响。
1 弹体撞击靶体有限元模型建立
1.1 材料本构关系和失效模型分析
弹体材料为经过热处理的38CrSi合金钢,其材料参数见表1[8],靶板材料为2A12-T4铝合金。由于38CrSi合金钢强度比2A12-T4铝合金强度大很多,弹体在撞击过程中几乎不发生变形及失效,可以认为是刚性的,因此,38CrSi钢的本构关系可通过双线性硬化模型进行描述,并可忽略温升和应变率的影响,表达式为
(1)
式中,σ 为应力;E 为弹性模量;Et 为切线模量;σ0 为屈服强度;ε0 为初始屈曲时的应变。
表1 38CrSi钢材料参数[8]
Tab.1 Material constants of 38CrSi steel[8]

弹性模量E(GPa)泊松比υ材料密度ρ(kg/m3)屈服强度σ0 (MPa)切线模量Et (GPa)2040.337 8501 90015
2A12-T4铝合金采用修改后的J-C本构模型和失效准则[9]进行描述,修改后的J-C本构模型对颈缩处进行了分段处理,如下式所示:
σeq=
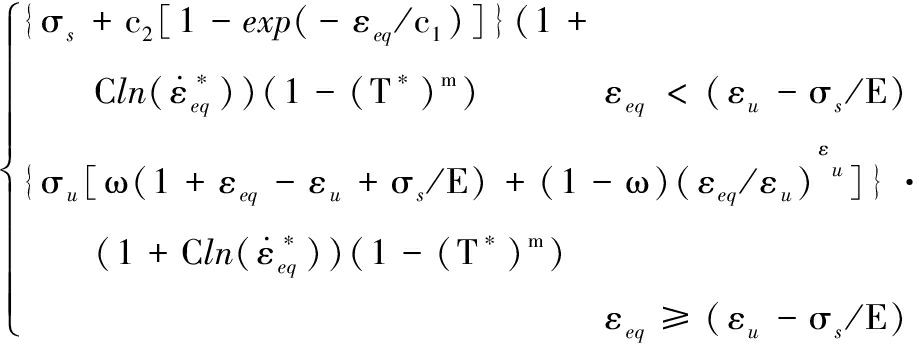
(2)
式中,σeq、εeq分别为等效应力、等效塑性应变;σs为材料屈服强度;![]() 为材料等效塑性应变率
为材料等效塑性应变率![]() 和参考应变率
和参考应变率![]() 之比;C、m分别为应变率敏感系数、温度软化系数;T
之比;C、m分别为应变率敏感系数、温度软化系数;T 为量纲一温度,T*=(T-Tr)/(Tm-Tr),Tr、Tm、T分别为参考温度、熔点和当前温度;σu、εu分别为颈缩时的真实应力、真实应变;c1、c2为材料参数;ω为权值,ω∈[0,1]。
为量纲一温度,T*=(T-Tr)/(Tm-Tr),Tr、Tm、T分别为参考温度、熔点和当前温度;σu、εu分别为颈缩时的真实应力、真实应变;c1、c2为材料参数;ω为权值,ω∈[0,1]。
对J-C失效准则温度项进行修改如下:
![]()
D5(1-exp(D6T*))]
(3)
σ*=(σ1+σ2+σ3)/(3σeq)
(4)
式中,εf为断裂应变;σ*为应力三轴度;D1、D2、D3为与应力三轴度相关的参数;D4为应变率影响系数;D5、D6为温度影响系数。
弹靶冲击过程中的材料温升公式如下:
(5)
式中,Cp为材料的质量定压热容;χ 为塑性功转热系数。
J-C失效模型中采用线性损伤演化模拟材料断裂的产生,其形式为
(6)
式中,Δεeq为在单位循环时间步内的有效塑性应变增量;εf为当前时间步范围内材料的断裂应变。
当线性损伤D达到1时,材料发生失效。
2A12-T4铝合金材料参数和模型参数见表2。
表2 2A12-T4材料参数[9]
Tab.2 Material constants of 2A12-T4[9]
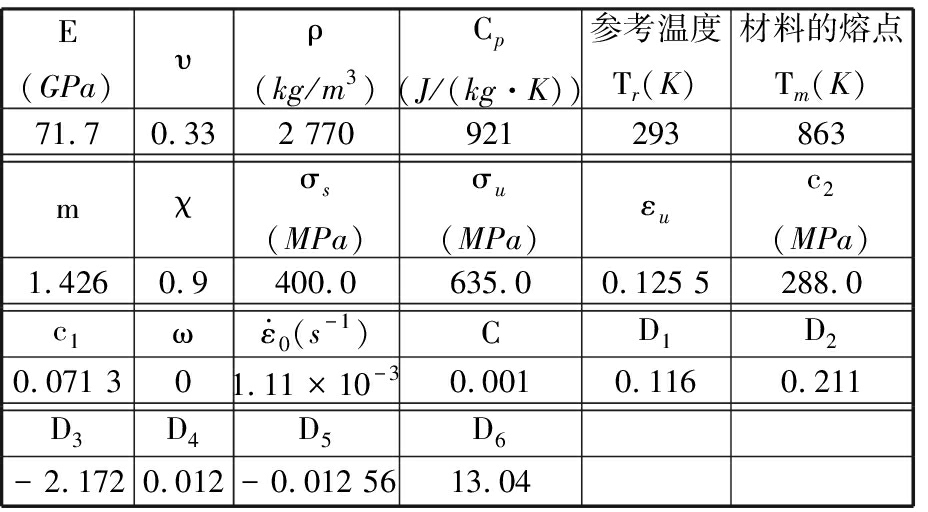
E(GPa)υρ(kg/m3)Cp(J/(kg·K))参考温度Tr(K)材料的熔点Tm(K)71.70.332 770921293863mχσs(MPa)σu(MPa)εuc2(MPa)1.4260.9400.0635.00.125 5288.0c1ωε·0(s-1)CD1D20.071 301.11×10-30.0010.1160.211D3D4D5D6-2.1720.012-0.012 5613.04
1.2 弹体与靶体几何模型建立
数值模拟与实验分析的弹靶材料和结构相同,初始撞击条件也相同。基于有限元软件ABAQUS/Explicit建立平头弹体冲击靶板模型,通过FORTRAN语言进行二次开发,编制VUMAT子程序嵌入运算程序中。弹体直径为12.62 mm,长度为37.8 mm,名义质量为34 g,其外形尺寸如图1所示。三角形波纹夹芯板的几何外形及尺寸如图2和表3所示,其中Tt为正面板(迎弹面)厚度,Tc为芯体厚度,Tb为背面板(背弹面)厚度,Hc为芯体高度,θ为芯体拓扑结构夹角。三角形波纹夹芯板与单层板的面密度均为16.62 kg/m2。弹体冲击靶体初始位置在节点处,如图3所示。
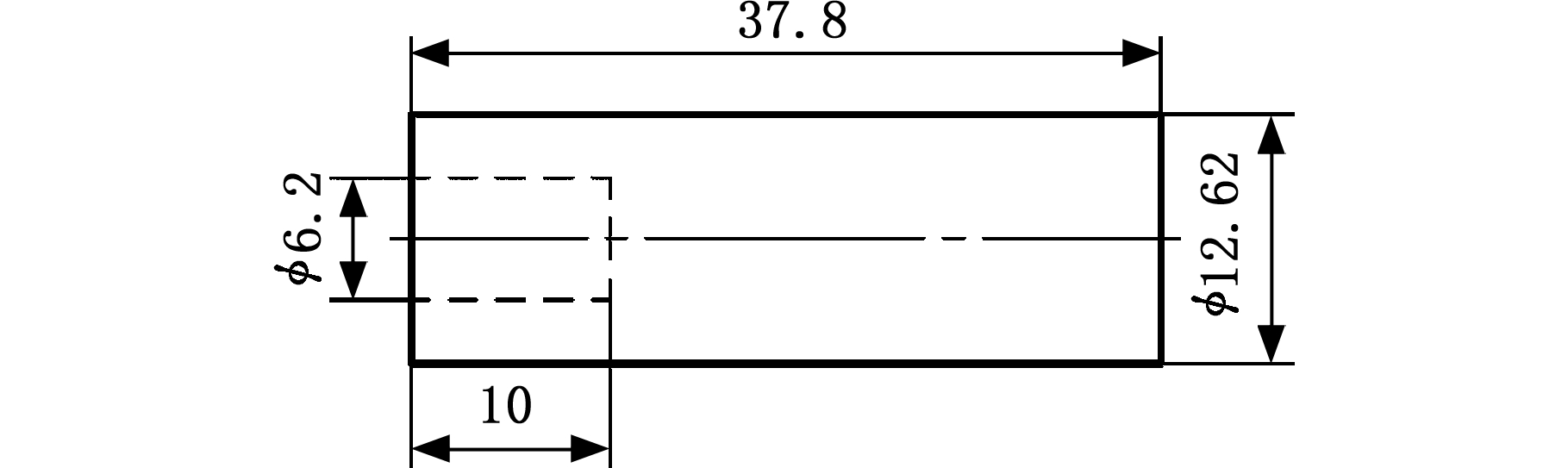
图1 弹体结构尺寸图
Fig.1 Structural dimension of projectile

图2 靶板结构尺寸
Fig.2 Structural dimension of target
表3 三角形波纹夹芯板几何尺寸
Tab.3 Geometry of triangle corrugated sandwich plate
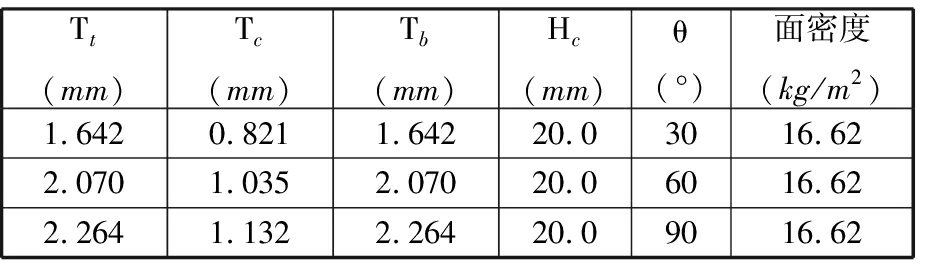
Tt(mm)Tc(mm)Tb(mm)Hc(mm)θ(°)面密度(kg/m2)1.6420.8211.64220.03016.622.0701.0352.07020.06016.622.2641.1322.26420.09016.62
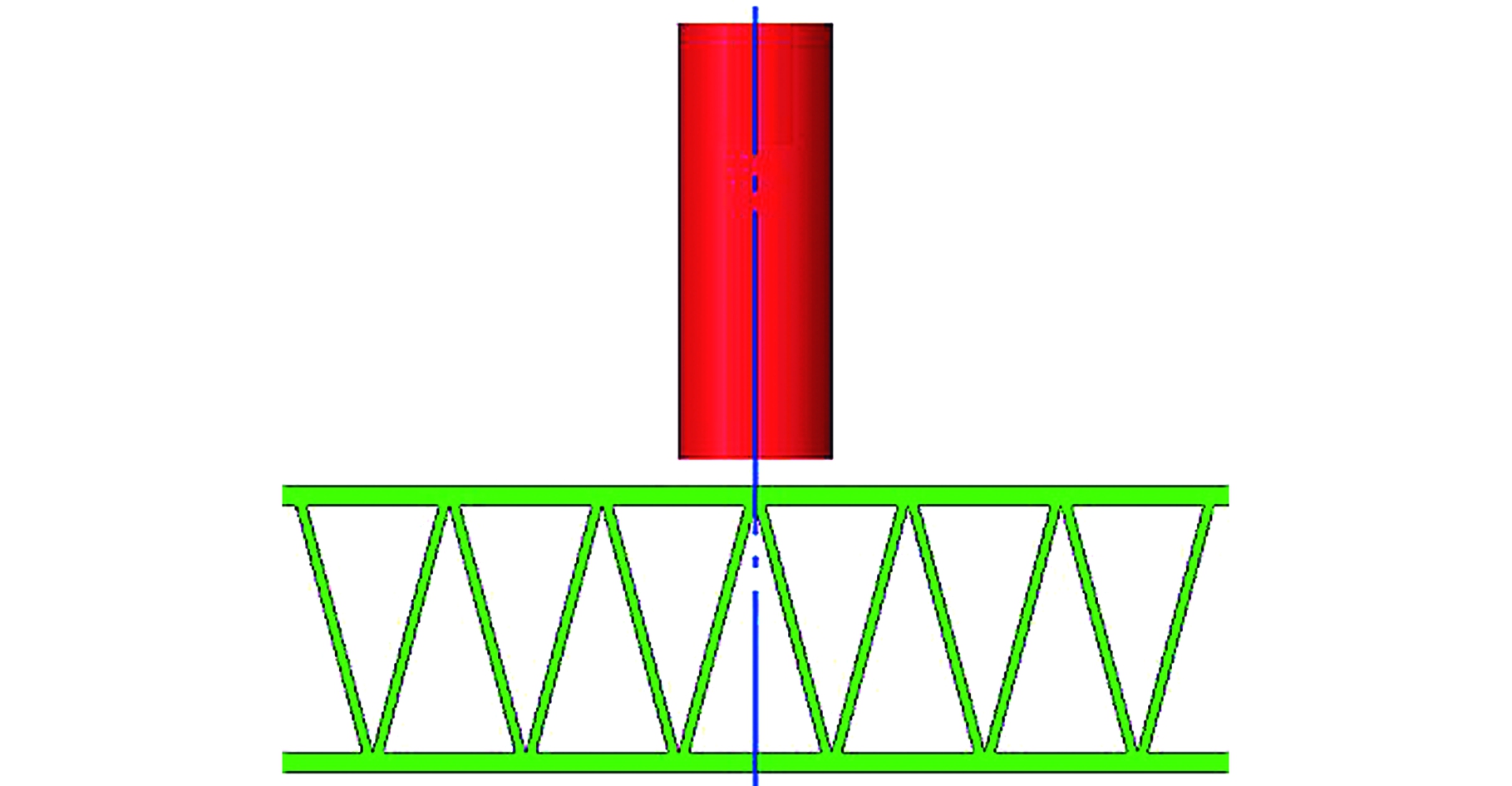
图3 弹靶冲击位置示意图
Fig.3 The position sketch of projectile impact plate
弹体与靶板单元类型均设定为C3D8R。弹体采用均匀化网格划分,单元尺寸为1 mm,并将其设置为刚体。靶板采用过渡网格,受弹体冲击的中心区域单元尺寸为0.2 mm,离冲击中心区域越远,单元尺寸越大,如图4所示。靶板冲击中心区域建立基于单元的面,设置弹体表面与靶心区域面自动接触,并通过Hard contact模式描述接触的法向行为。将弹靶间滑动摩擦因数设置为0(即忽略摩擦效应的影响)[10-11]。此外,正背面板及芯体间采用Tie连接[11],使得面板与芯体连接处的节点具有相同平动和转动自由度,以保证波纹夹芯板结构的完整性和应力波的正常传递。
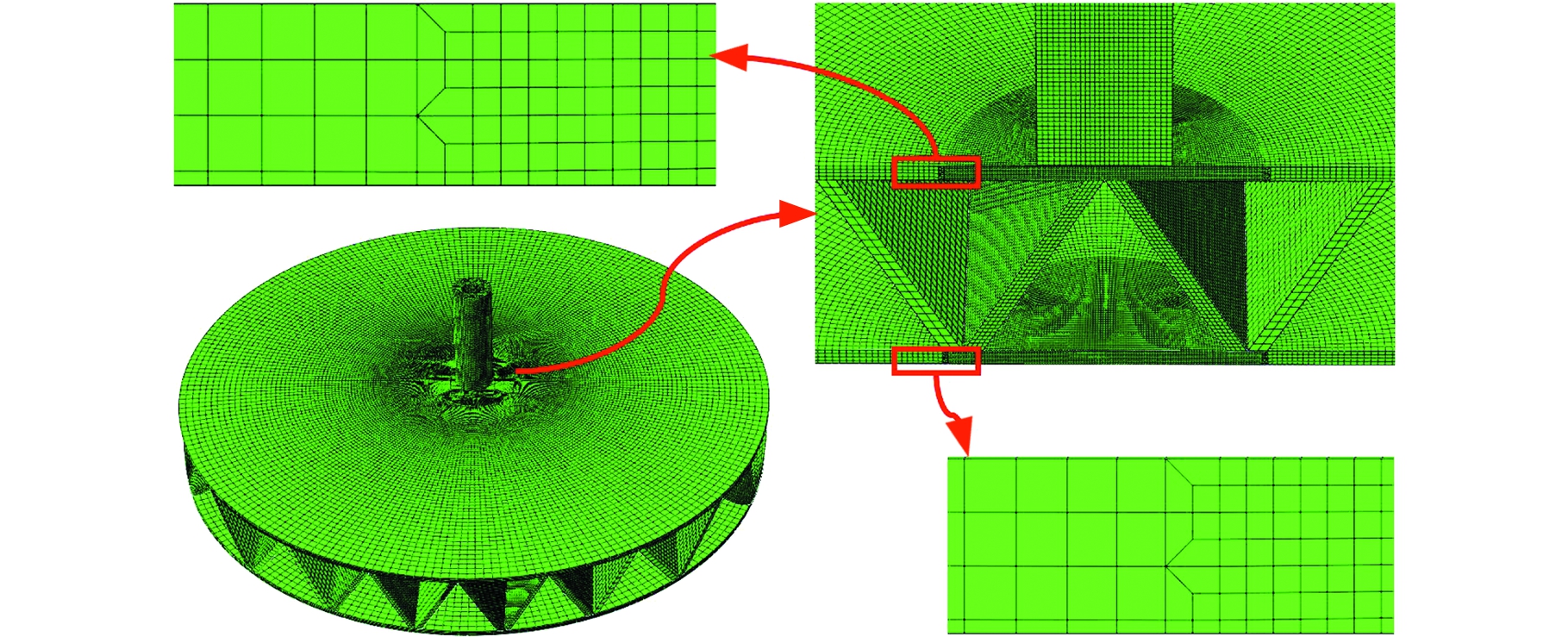
图4 弹靶几何模型及网格形式
Fig.4 Geometry and finite element mode of target
and projectile
1.3 模型有效性验证
利用一级气炮系统开展平头弹体对单层板与夹芯板的冲击试验,对比数值模拟与试验结果,以验证数值模拟模型及其参数的有效性,试验系统如图5所示。
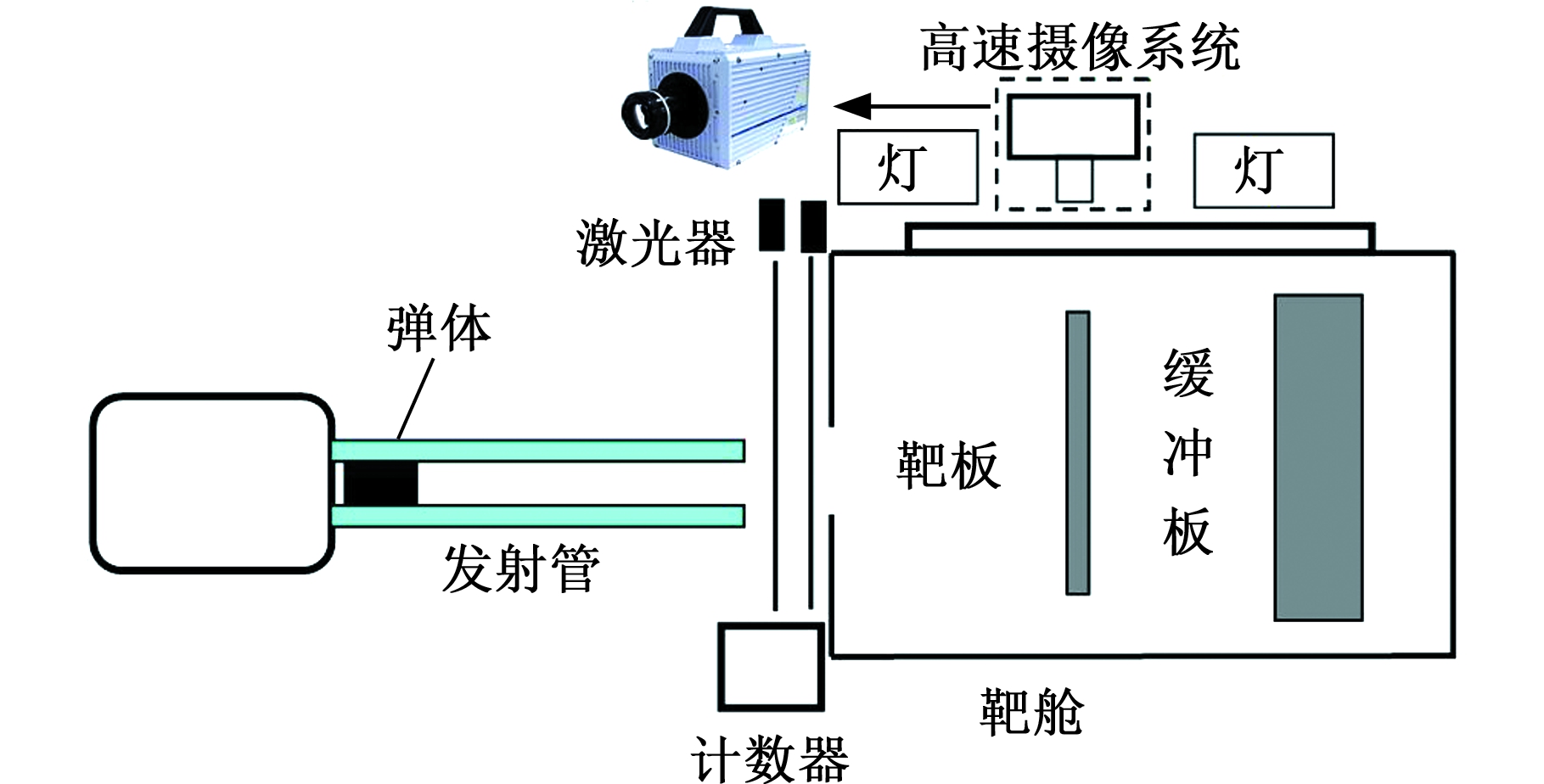
图5 一级气炮系统
Fig.5 One-stage gas gun system
利用Recht-Ipson公式[12],通过最小二乘法拟合弹体贯穿靶板的初始速度与剩余速度数据,得到
(7)
a=mp/(mp+mpl)
式中,vi、vr分别为弹体初始速度与剩余速度;vbl为弹道极限速度;mp为弹体质量;mpl为冲塞质量;c为待定常数。
研究弹靶冲击损伤特性主要考虑弹道极限速度和失效模式。图6对比了平头弹体冲击靶体试验与数值模拟的速度数据。经过计算,单层板数值模拟与试验的弹道极限速度分别为151.0 m/s与144.0 m/s,两者相差4.8%,三角形波纹板 ( θ=30° ) 数值模拟与试验的弹道极限速度分别为123 m/s与115.0 m/s,两者相差6.9%。可以发现,单层板及夹芯板数值模拟与试验的初始速度-剩余速度曲线比较吻合,并且曲线变化趋势一致。
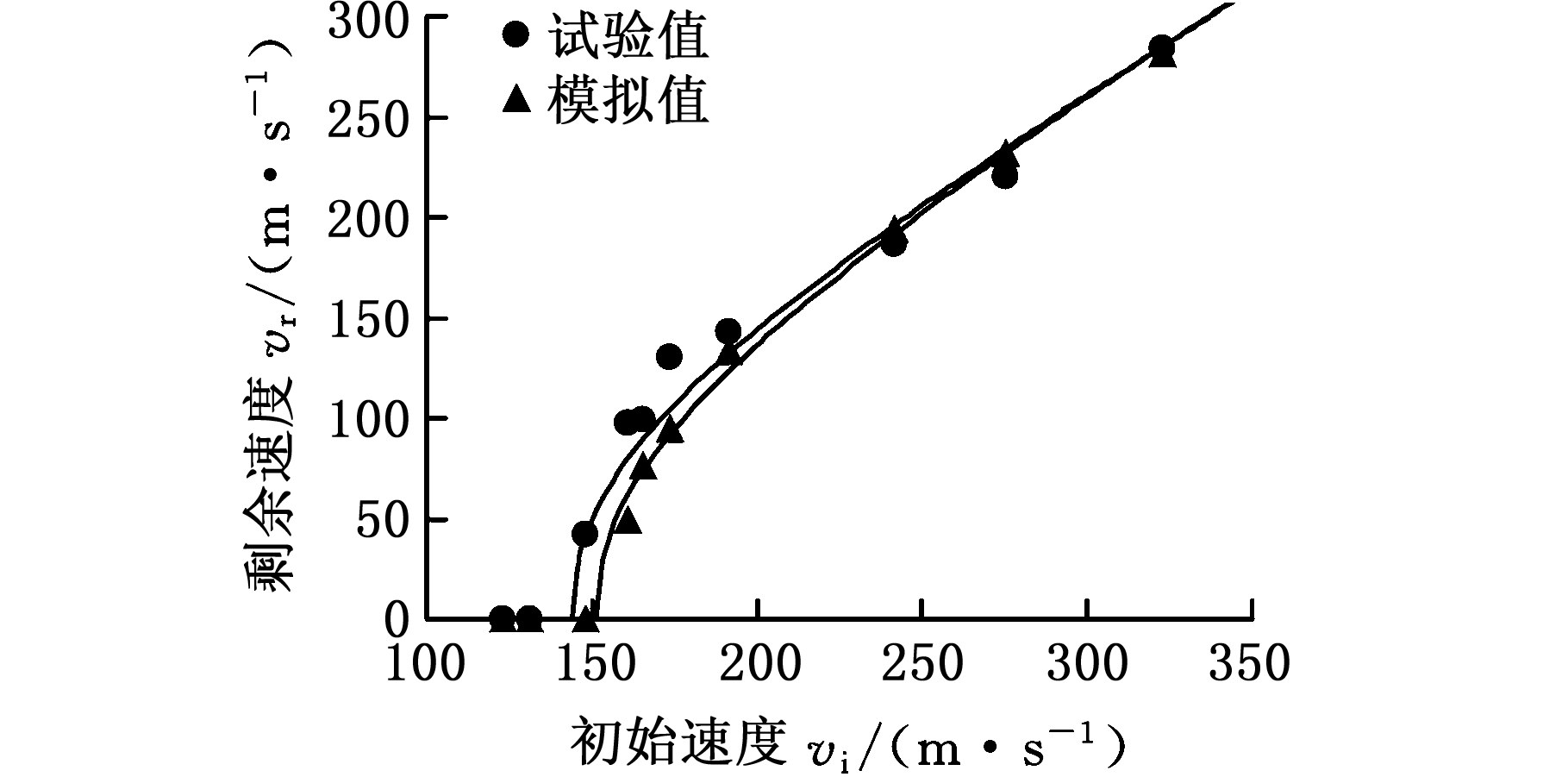
(a)单层板
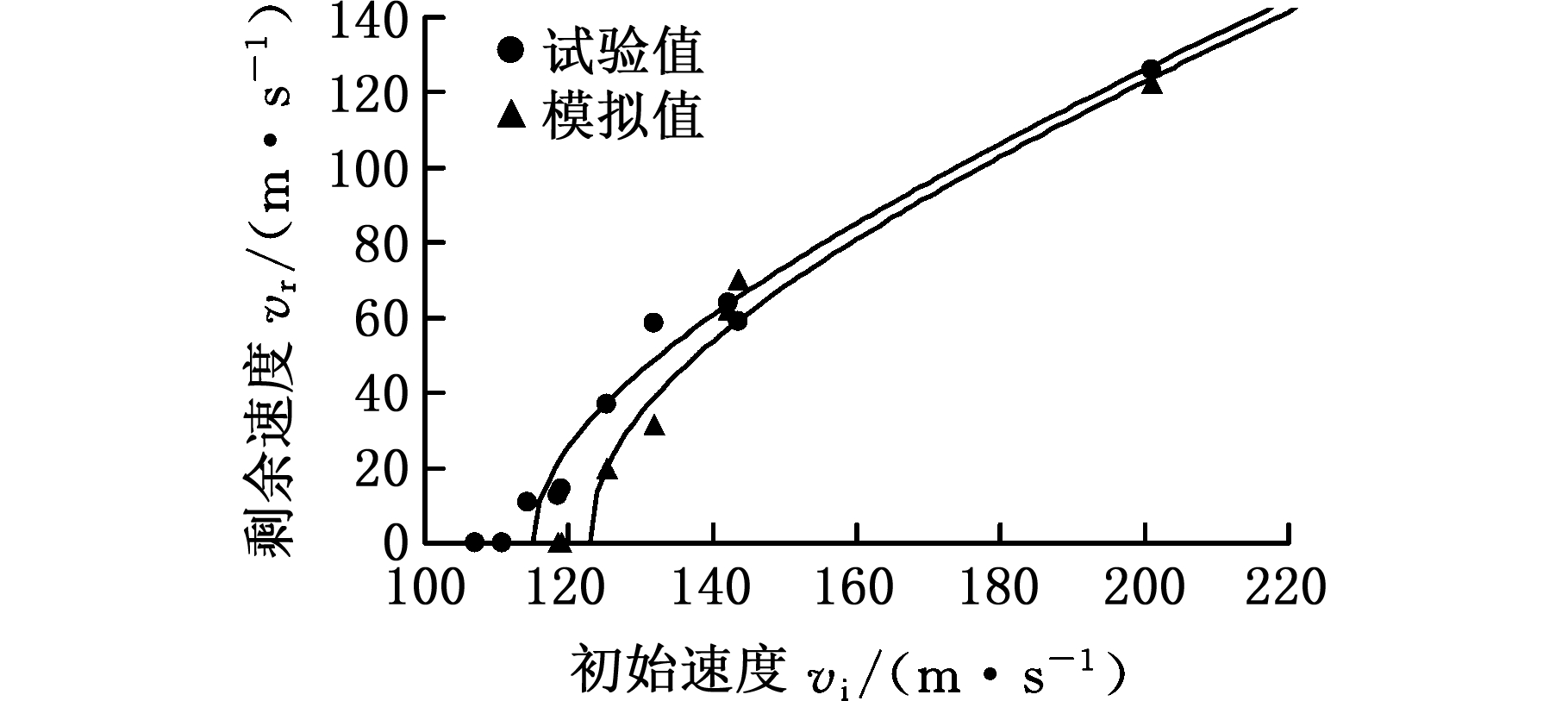
(b)三角形波纹夹芯板
图6 弹体速度试验与数值模拟对比
Fig.6 Comparisons of projectile velocity between
experiment and simulation
此外,通过冲击试验发现,单层板弹道极限速度比三角形波纹板弹道极限速度提高22.7%,而数值模拟发现,单层板弹道极限速度比三角形波纹板弹道极限速度提高25.2%,两者之间接近,这也说明了采用合适的数值模拟模型及参数可以有效地分析靶体结构对其抗冲击特性的影响。
图7对比了弹体冲击靶板试验与数值模拟的过程与失效模式。单层板主要发生局部隆起变形和冲塞破坏,并且数值模拟能较好地预测到靶板背面的拉伸撕裂现象与少量的微裂纹,如图7a 所示。三角形波纹夹芯板主要发生冲塞与拉伸撕裂破坏,前面板弹孔规则,而后面板弹孔表现出明显的撕裂特征,弹孔不规则,如图7b 所示。
2 数值计算结果及分析
2.1 弹道极限速度分析
表4所示为根据式(7) 拟合数值模拟结果得到的模型参数,其中T30、T60与T90分别表示靶体芯体拓扑结构夹角为30°、60°及90°。对比单层板及三角形波纹夹芯板的弹道极限速度可以发现,单层板的弹道极限速度大于三角形波纹夹芯板的弹道极限速度。单层板与T30、T60及T90相比,弹道极限速度分别提高22.8%、18.9%及9.4%,这也就是说靶体几何形状对其抗冲击性能存在显著的影响。

(a)单层板(vi=241.5 m/s)
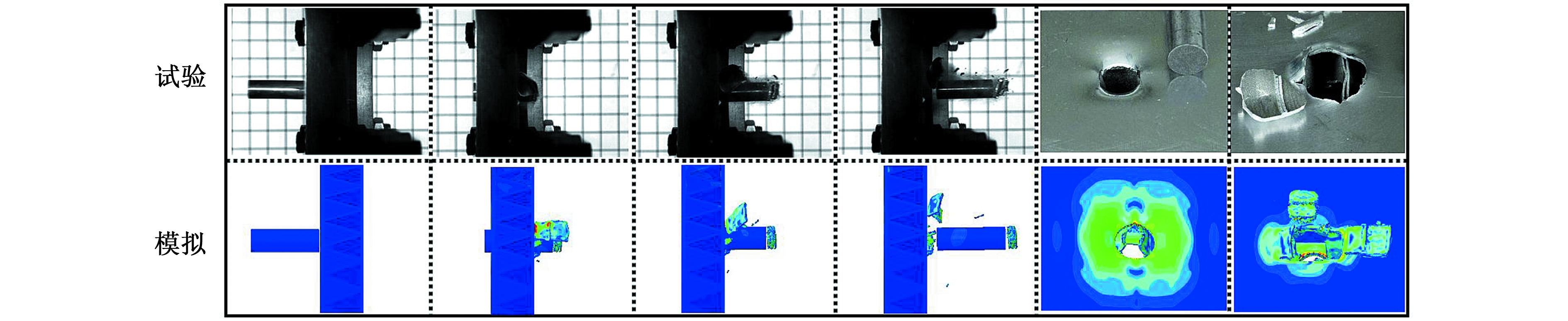
(b)三角形波纹夹芯板(vi=143.6 m/s)
图7 试验与数值模拟的弹靶冲击过程及靶板失效模式对比
Fig.7 Comparisons of impact process and failure mode of plates impacted by projectile between experiment and simulation
图8给出了平头弹体冲击靶板的初始速度-剩余速度曲线,可以发现靶板的几何形状对其抗冲击性能存在影响,弹道极限速度随着靶板芯体拓扑结构夹角增大而增大。T90、T60与T30相比,弹道极限速度分别提高3.3%和12.2%。此外,随着弹体初始速度增大,平头弹体冲击不同类型靶板的初始速度-剩余速度曲线趋于接近,即靶板几何形状对其抗冲击性能的影响随弹体初始速度增大而减小。
表4 弹体冲击三角形波纹夹芯板的模型参数
Tab.4 Model parameters of circular corrugated sandwich plates impacted by projectiles

模型类型acvbl(m/s)T300.941.95123.0T600.941.85127.0T900.952.00138.0
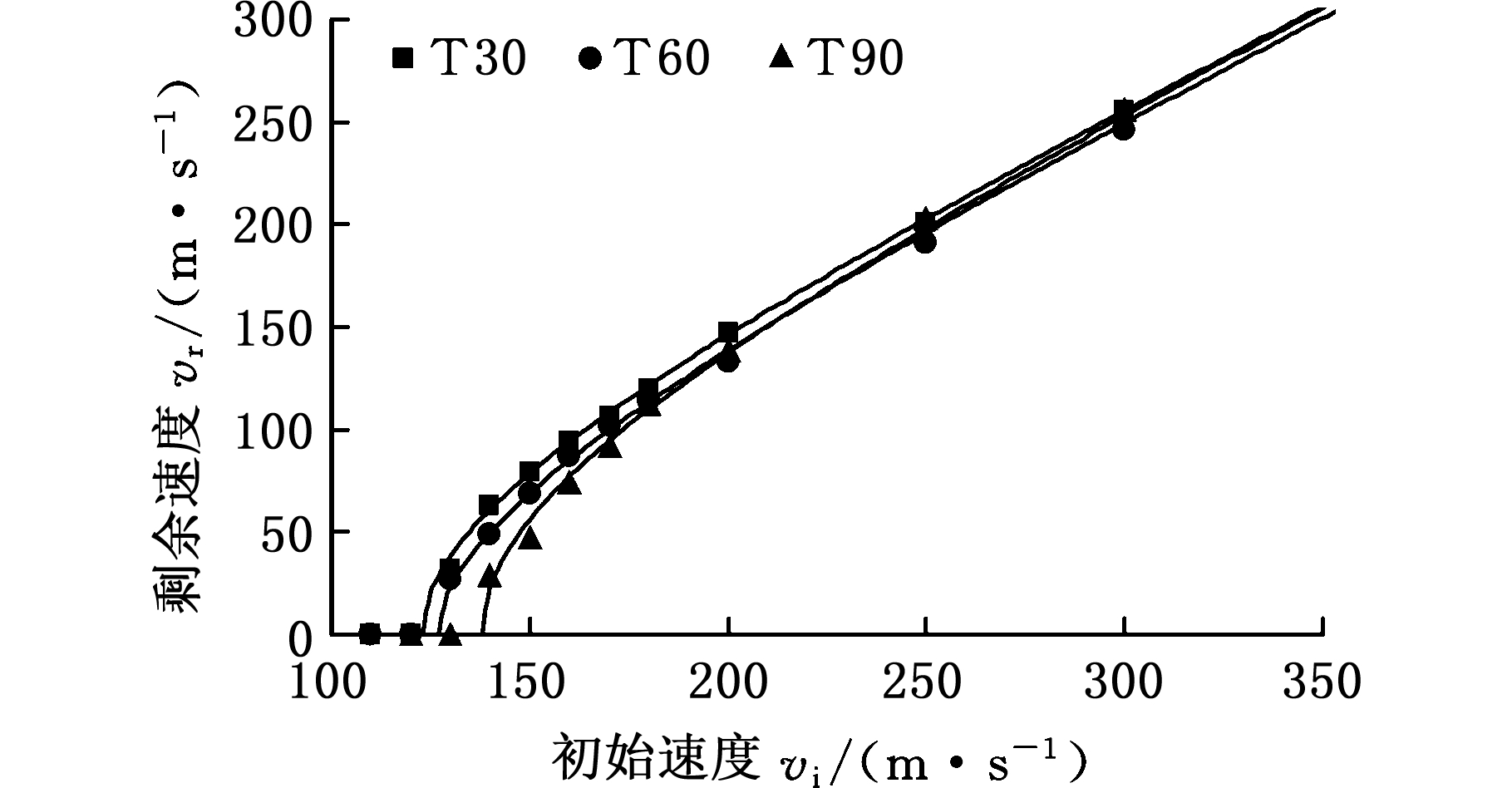
图8 弹体初始速度-剩余速度曲线对比
Fig.8 Residual velocity vs. initial velocity
curve for projectiles
2.2 靶板冲击失效特性分析
图9给出了三角形波纹夹芯板的冲击损伤形貌,可以发现靶板正面板产生剪切冲塞破坏,并伴随有局部凹坑变形产生,断口规则,但是,芯体产生屈曲变形与拉伸撕裂破坏。此外,背面板产生撕裂破坏,断口周围存在明显的局部隆起变形,并伴随有不同程度的径向、纵向与周向裂纹扩展。随着芯体拓扑结构夹角的增大,正面板凹坑变形量及变形面积有所增加。芯体由整个单元的压溃与拉伸撕裂破坏转变为中上部拉伸撕裂破坏,而拓扑结构夹角较大时,顶部发生局部屈曲变形与拉剪冲塞破坏。背面板局部隆起变形量有所增大,撕裂破坏明显降低。

(a)T30(vi=140 m/s)

(b)T30(vi=300 m/s)
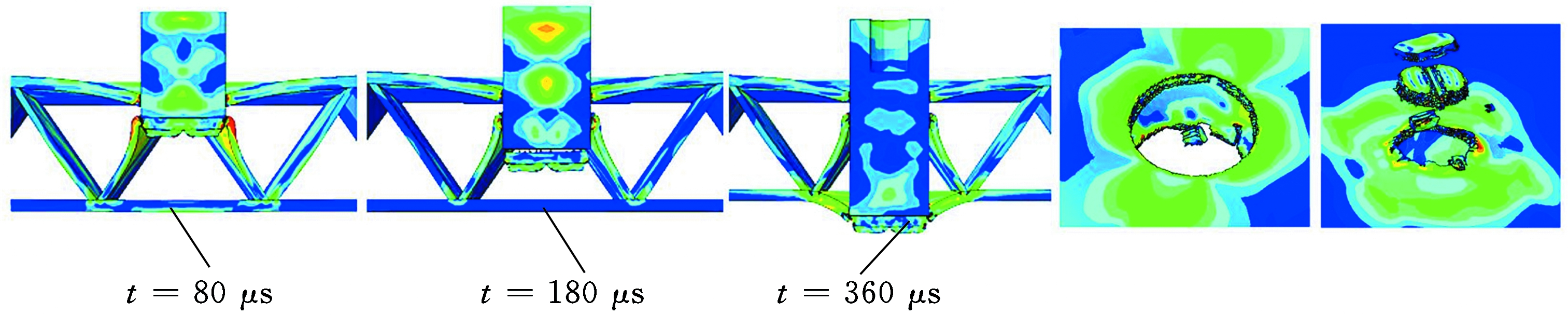
(c)T60(vi=140 m/s)
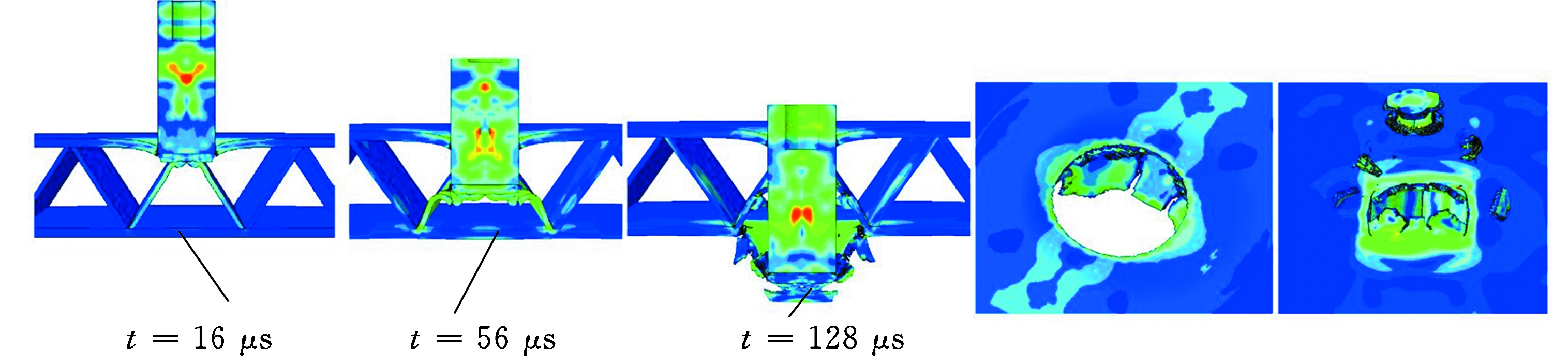
(d)T60(vi=300 m/s)

(e)T90(vi=140 m/s)

(f)T90(vi=300 m/s)
图9 弹体撞击靶板失效模式
Fig.9 Failure mode of plates impacted by projectiles
2.3 靶板能量吸收分析
靶板冲击过程中耗能Ea通过弹体的动能变化量ΔE来表示:
式中,Ei、Er分别为初始速度和剩余速度下弹体的动能。
图10所示为三角形波纹夹芯板不同部分的耗能对比,可以发现靶板芯体耗能普遍高于面板耗能。随着芯体拓扑结构夹角增大,正面板与背面板耗能均增加,而芯体耗能减少。
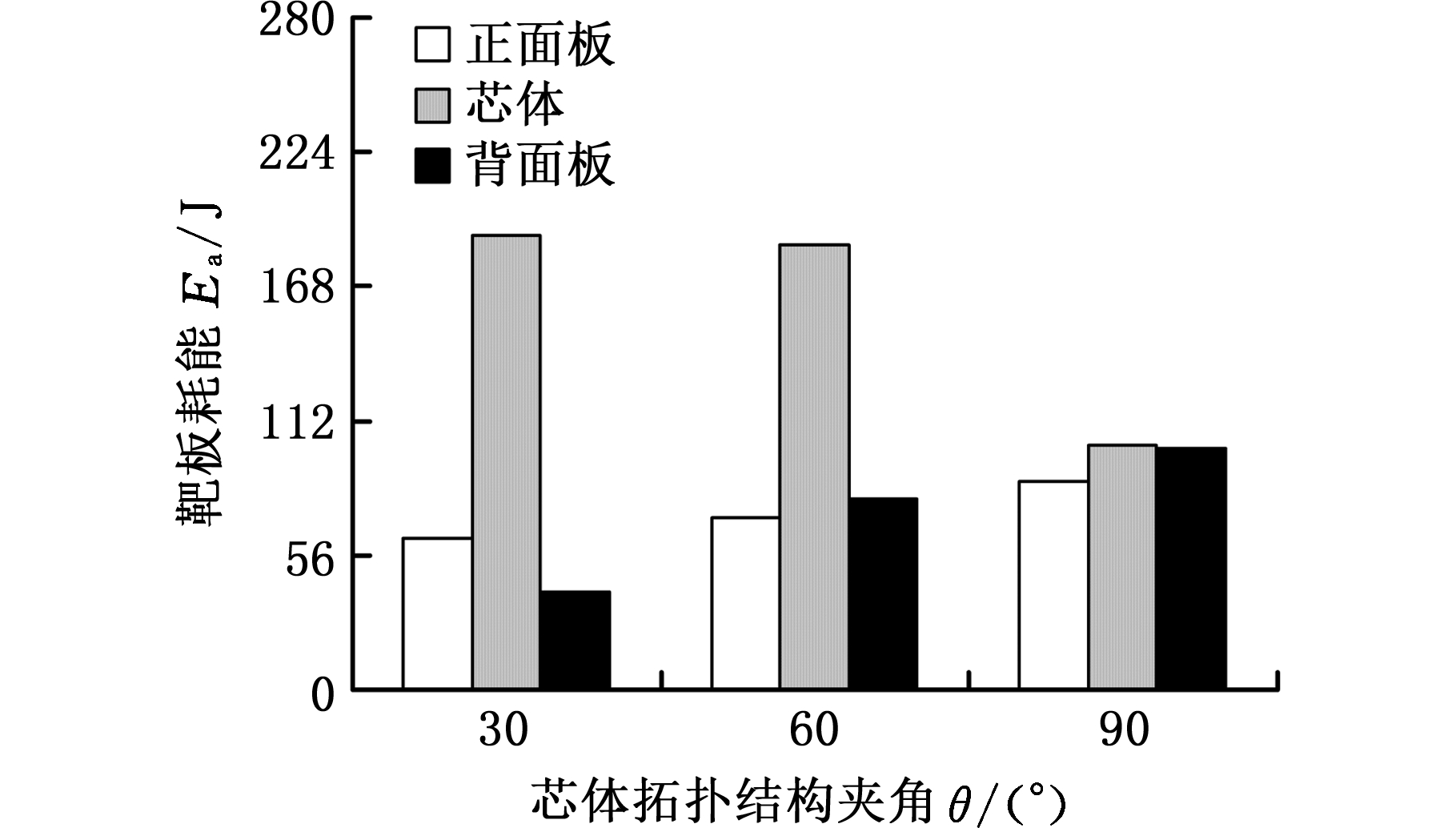
图10 三角形波纹夹芯板不同部分耗能对比
(vi=200 m/s)
Fig.10 Energy absorption comparison of various
parts of triangle corrugated sandwich plates
(vi=200 m/s)
3 结论
(1)建立了平头弹体冲击三角形波纹夹芯板的数值模拟模型,基于冲击试验验证了模型及其参数的有效性,通过数值模拟计算揭示了靶板几何形状对其抗冲击特性的影响。
(2)靶板的几何尺寸及结构对其抗冲击性能存在显著影响,单层板抗冲击性能高于等密度的三角形波纹夹芯板抗冲击性能。单层板与三角形波纹夹芯板T30、T60及T90相比,弹道极限速度分别提高22.8%、18.9%及9.4%。
(3)增加三角形波纹夹芯板的芯体拓扑结构夹角能够提高其抗冲击性能,T90及T60比T30弹道极限速度分别提高3.3%及12.2%,但是,夹芯板几何形状对其抗冲击性能的影响随弹体初始速度增大而减小。
(4)三角形波纹夹芯板正面板发生剪切冲塞与局部凹坑变形破坏,芯体发生屈曲变形与拉伸撕裂破坏,而背面板产生剪切冲塞和拉伸撕裂破坏。
(5)弹体速度对靶板能量的耗散存在影响,面板耗能随着弹体初始速度增大而增大,而芯体耗能随着弹体初始速度增大而减小。三角形波纹夹芯板芯体的耗能明显高于面板的耗能。此外,随着靶板芯体拓扑结构夹角增大,正面板与背面板耗能均增加,而芯体耗能减少。
[1] ZHANG P, CHENG Y, LIU J, et al. Experimental and Numerical Investigations on Laser-welded Corrugated-core Sandwich Panels Subjected to Air Blast Loading[J]. Marine Structures, 2015, 40: 225-246.
[2] 任鹏, 田阿利, 张伟. 水下冲击载荷下波纹夹层结构动态响应特性分析[J]. 振动与冲击, 2016,35(23):90-94.
REN Peng, TIAN Ali, ZHANG Wei. Dynamic Response Characteristics of a Corrugated Core Sandwich Panel Subjected to Underwater Shock Loading[J]. Journal of Vibration and Shock, 2016, 35(23): 90-94.
[3] RIMOLI J J, TALAMINI B, WETZEL J J, et al. Wet-sand Impulse Loading of Metallic Plates and Corrugated Core Sandwich Panels[J]. International Journal of Impact Engineering, 2011, 38(10): 837-848.
[4] PANIGRAHI S K, DAS K. Ballistic Impact Analyses of Triangular Corrugated Plates Filled with Foam Core[J]. Advances in Computational Design, 2016, 1(2): 139-154.
[5] HOLMEN J K, BORVIK T, HOPPERSTAD O S. Experiments and Simulations of Empty and Sand-filled Aluminum Alloy Panels Subjected to Ballistic Impact[J]. Engineering Structures, 2017, 130: 216-228.
[6] 周昊, 郭锐, 南博华,等. 填充式波纹夹层结构超高速撞击特性仿真[J]. 国防科技大学学报, 2017, 39(2):57-63.
ZHOU Hao, GUO Rui, NAN Bohua, et al.Simulation on Hypervelocity Impact Characteristics of Stuffed Corrugation-cored Sandwiches[J]. Journal of National University of Defense Technology, 2017, 39(2):57-63.
[7] 邓泽华, 郭锐, 周昊,等. 梯度波纹夹层防护结构超高速碰撞特性仿真研究[J]. 航天器环境工程, 2018, 35(1):7-13.
DENG Zehua, GUO Rui, ZHOU Hao, et al.Simulation of Hypervelocity Impact Characteristics of Gradient Corrugated-core Sandwich Plates[J]. Spacecraft Environment Engineering, 2018, 35(1):7-13.
[8] BORVIK T, HOPPERSTAD O S, BERSTAD T, et al. A Computational Model of Viscoplasticity and Ductile Damage for Impact and Penetration[J]. European Journal of Mechanics A: Solids, 2001, 20(5):685-712.
[9] 张伟, 魏刚, 肖新科. 2A12铝合金本构关系和失效模型[J]. 兵工学报, 2013, 34(3):276-282.
ZHANG Wei, WEI Gang, XIAO Xinke.Constitutive Relation and Fracture Criterion of 2A12 Aluminum Alloy[J]. Acta Armamentarii, 2013, 34(3):276-282.
[10] DENG Y F, LI J F, JIA B H, et al. Numerical Study of Failure Modes and Crack Propagation in 2A12 Aluminum Target against Blunt-nosed Projectile at Low Yaw Angle[J]. Strength of Materials, 2016, 48(6): 834-849.
[11] BABAKHANI A, GOLESTANIPOUR M, ZEBARJAD S M. Modelling of Aluminum Foam Core Sandwich Panels under Impact Perforation[J]. Materials Science and Technology,2016, 32(13): 1330-1337.
[12] RECHT R F, IPSON T W. Ballistic Perforation Dynamics[J]. Journal of Applied Mechanics-Transactions ASME, 1963, 30: 385-391.
