0 引言
丝杠作为旋转运动与直线运动互相转换的重要传动零件,因具有传动精度高、刚性好、传动扭矩大等优点,在装备制造、航空航天、轻工等领域得到了广泛的应用。目前丝杠的加工方法主要有切削加工和挤压成形,切削加工不仅生产效率低、材料利用率低,且切削加工导致金属纤维断裂,降低了丝杠的强度和承载能力;挤压加工方法具有节省材料、成形件耐磨性好、热处理变形小的优点,经济效益与社会效益较好[1-2],但所需要的设备吨位大、能耗大、噪声大,且成形时金属流动比较困难。冷滚打成形技术的出现有效解决了上述问题[3],已成为国内外学者研究的主要课题。
ABDULLAH 等[4]对自动生产线中利用冷滚打方法大批量生产矩形花键进行了研究,并深入探讨了该加工工艺,对加工零件的精度进行了分析。LIU等[5]对利用冷滚打方法加工内花键进行了研究,指出了冷滚打内花键的滚打轮与冷滚打外花键的滚打轮的区别。张璐等[6-7]利用ABAQUS软件建立了冷滚打板料、齿条和齿形的有限元模型,通过对冷滚打过程进行数值模拟得到了冷滚打成形力;同时利用解析方法计算了冷滚打成形力,并利用有限元软件ABAQUS对解析方程进行了修正,最后通过试验得到了冷滚打成形力。崔凤奎等[8-11]深入研究了花键冷滚轧成形机理,根据有限元模拟结果揭示了花键冷滚轧过程中金属流动规律并获得了弹性恢复量的大小,同时利用显式中心差分算法,采用有限元软件ANSYS/LS-DYNA对该成形过程进行数值模拟,实现了成形过程的可视化,通过对数值模拟结果的分析和讨论,提出了轴坯直径的修改方法,揭示了花键冷滚打成形过程中金属流动规律和应力变化情况。张璐等[12]通过对冷滚打成形过程进行三维数值模拟和实验,得到了丝杠冷滚打成形的应变场、应力场分布和工件硬化层、硬度分布以及金相组织变形,并对其进行了深入分析。李玉玺等[13]利用DEFORM软件对40Cr的冷滚打过程进行有限元模拟,揭示了高速冷滚打成形的应力、应变、温度及金属流动变化规律。
本文在丝杠冷滚打成形原理的基础上,根据丝杠与滚打轮的空间和运动关系建立有限元仿真模型,通过仿真获得滚打轮半径、滚打轮圆角半径和打入量对成形过程中变形力的影响规律,并通过实验进行了验证。
1 冷滚打成形丝杠基本原理
丝杠冷滚打成形是一个高速、瞬态、强冲击、大变形的复杂成形过程,其原理如图1所示。丝杠冷滚打加工是通过具有一定形状的滚打轮对丝杠毛坯进行局部断续滚压和击打使毛坯产生塑性变形,通过累积效应而在工件上形成丝杠螺旋滚道的一种加工工艺。其中,滚打轮安装在高速旋转的滚打轴上,并可绕自身轴线自转。滚打轮接触工件的瞬间,在工件与滚打轮之间摩擦力的作用下,滚打轮自转,实现滚打轮和工件之间的滚动。图1中β为丝杠螺旋升角。当滚打轮击打工件即滚打轮与工件接触时,滚打轮自转速度由接触时的摩擦力和工件公转速度确定,滚打轮和工件之间的纯滚动运动保证了丝杠成形件的表面质量和滚打轮的使用寿命。

图1 丝杠冷滚打工作原理
Fig.1 The principle of leadscrew’s cold roll-beating
丝杠冷滚打成形是一个不断累积成形的过程,每一次滚打可以划分为三个阶段:打入阶段、稳定滚打阶段、打出阶段。由冷滚打原理分析可知,丝杠冷滚打的主要运动有:滚打轴的旋转运动(转速nw),工件的旋转运动(转速nr),滚打轮的自转运动(转速ns),滚打轮相对于工件的轴向进给运动(进给速度vf)。在滚打过程中,工件以一定转速转动,滚打轮可随滚打轴沿轴向以一定速度进给,工件在固定位置作连续转动。
2 有限元仿真模型的建立
2.1 几何模型
利用ABAQUS有限元仿真软件进行几何模型建立,滚打轮直径为45 mm、宽度为4 mm,滚打轮外缘为圆弧形,其半径为2.14 mm,滚打轮的回转半径为65 mm;拟成形工件为直径40 mm、导程10 mm的右旋丝杠。为了简化模型,滚打过程中,将滚打轮和滚打轴视为一体,假定滚打轮和工件接触过程中不自转。滚打轮和滚打轴均视作刚体。模拟过程中的自转动力由十字形动力轴提供,为了提高计算效率,在不影响计算精度的前提下,把工件简化为十字空心筒,这样既解决了动力传输问题,又可以减少网格划分数量。最终模型如图2所示,十字形动力轴如图3所示。

图2 模型图
Fig.2 Model diagram

图3 十字形动力轴
Fig.3 Cross power shaft
2.2 材料模型
工件材料选用40Cr,实验前对工件的物理参数进行测量,如表1所示。滚打轮材料通常为W6Mo5Cr4V2Co8、W14Cr4V4、W18Cr4V等,热处理后硬度要求达到62~64HRC,其刚度和硬度远远高于工件,成形过程中几乎不发生变形,因此将滚打轮定义为刚体部件。根据成形过程中的变形特点,材料选择Johnson-Cook本构方程能有效反映丝杠在高应变速率下的应变效应、应变速率效应和温度效应。Johnson-Cook模型如下:
式中,![]() 为材料屈服应力;A为参考温度和参考应变率下(准静态下) 的屈服强度;B为应变硬化系数;n为应变硬化指数;C为应变率硬化系数;m为热软化指数;
为材料屈服应力;A为参考温度和参考应变率下(准静态下) 的屈服强度;B为应变硬化系数;n为应变硬化指数;C为应变率硬化系数;m为热软化指数;![]() 为等效塑性应变;εp为塑性应变;ε0为参考应变;
为等效塑性应变;εp为塑性应变;ε0为参考应变;![]() 为量纲一塑性应变率;
为量纲一塑性应变率;![]() 为参考应变率;
为参考应变率;![]() 为塑性应变率;T*为相对温度;Tr为参考温度;Tm为材料的熔点;T为瞬时温度。
为塑性应变率;T*为相对温度;Tr为参考温度;Tm为材料的熔点;T为瞬时温度。
Johnson-Cook模型参数如表2所示。
表1 丝杠工件物理参数
Tab.1 Physical parameters of the leadscrew work piece
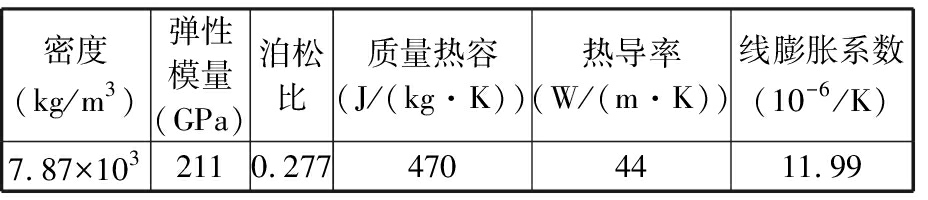
密度(kg/m3)弹性模量(GPa)泊松比质量热容(J/(kg·K))热导率(W/(m·K))线膨胀系数(10-6/K)7.87×1032110.2774704411.99
表2 40Cr材料Johnson-Cook模型参数
Tab. 2 40Cr material Johnson-Cook model parameters
A(MPa)B(MPa)CmnTr(℃)ε·0(s-1)Tm(℃)9052260.030.830.21200.0041 673
2.3 单元类型选择与网格划分
网格质量的好坏直接关系到分析是否能够顺利、快速地完成,也关系到能否得到高精度的分析结果。为了保证仿真的准确、高效,在丝杠滚打区域将网格细化,在靠近传动刚体的部位将网格适当放大,并选用显式线性3DStress六面体单元C3D8R对工件进行网格划分,最终划分单元数为670 000;其中滚打轮和十字形动力轴均为三维解析性旋转刚性壳体,网格划分结果如图4所示。

图4 工件网格划分结果
Fig.4 Result of meshing the workpiece
2.4 接触、摩擦与边界条件及相关假设
在滚打过程中,滚打轮表面与工件圆周表面的接触为面-面接触,主面为刚度较大的滚打轮表面,从面为工件表面。接触面之间的相对滑动关系设为有限滑移,由于摩擦主要发生在切向,因此采用剪切摩擦;设置摩擦因数为0.2,摩擦模型选择罚摩擦公式;接触面的法向作用选择硬接触。
在边界条件定义中,丝杠工件只绕其轴心旋转,而旋转动力由十字形动力轴提供,定义十字形动力轴只绕其轴心旋转,同时约束其他5个自由度;约束工件两个端面的位移自由度,其他5个自由度不约束;滚打轮包含两个运动,一个运动是绕参考点的旋转运动,另一个为平行于工件轴线的进给运动。为了提高计算效率、节省时间,采用单次与多次滚打相结合的方法进行仿真。
3 仿真结果分析
3.1 单次滚打结果分析
通过有限元仿真获得单次滚打结果时,滚打轮半径Rs对Mises应力影响规律如图5所示,随滚打轮半径从10 mm增大到18 mm,Mises应力增大,成形力也随之增大。同样可以获得滚打轮圆角半径r和打入量f对Mises应力的影响规律:滚打轮的圆角半径r增大,Mises应力增大;打入量f增大,Mises应力增大,其中应力云图与滚打轮半径增大时相似,不再一一列举。
3.1.1 滚打轮半径对变形力的影响
在有限元模拟中分别设置5个不同的滚打轮半径,分别为10 mm、12mm、14 mm、16 mm、18 mm,滚打轮转速ns=1000 r/min,滚打轮圆角半径r=1.5 mm,单次滚打过程打入量f=1 mm不变。图6为滚打轮半径不同时单次滚打过程变形力的变化曲线。
滚打轮半径增大,单次滚打过程中变形力及其在切向和径向的最大值随之增大。滚打轮半径增大,滚打轮与工件之间的接触面积改变,变形力随之而变,单次滚打过程中接触面积的最大值增大,必然引起单次滚打变形力的最大值增大。滚打轮半径变化,摩擦力随之变化,进而影响到变形力变化。
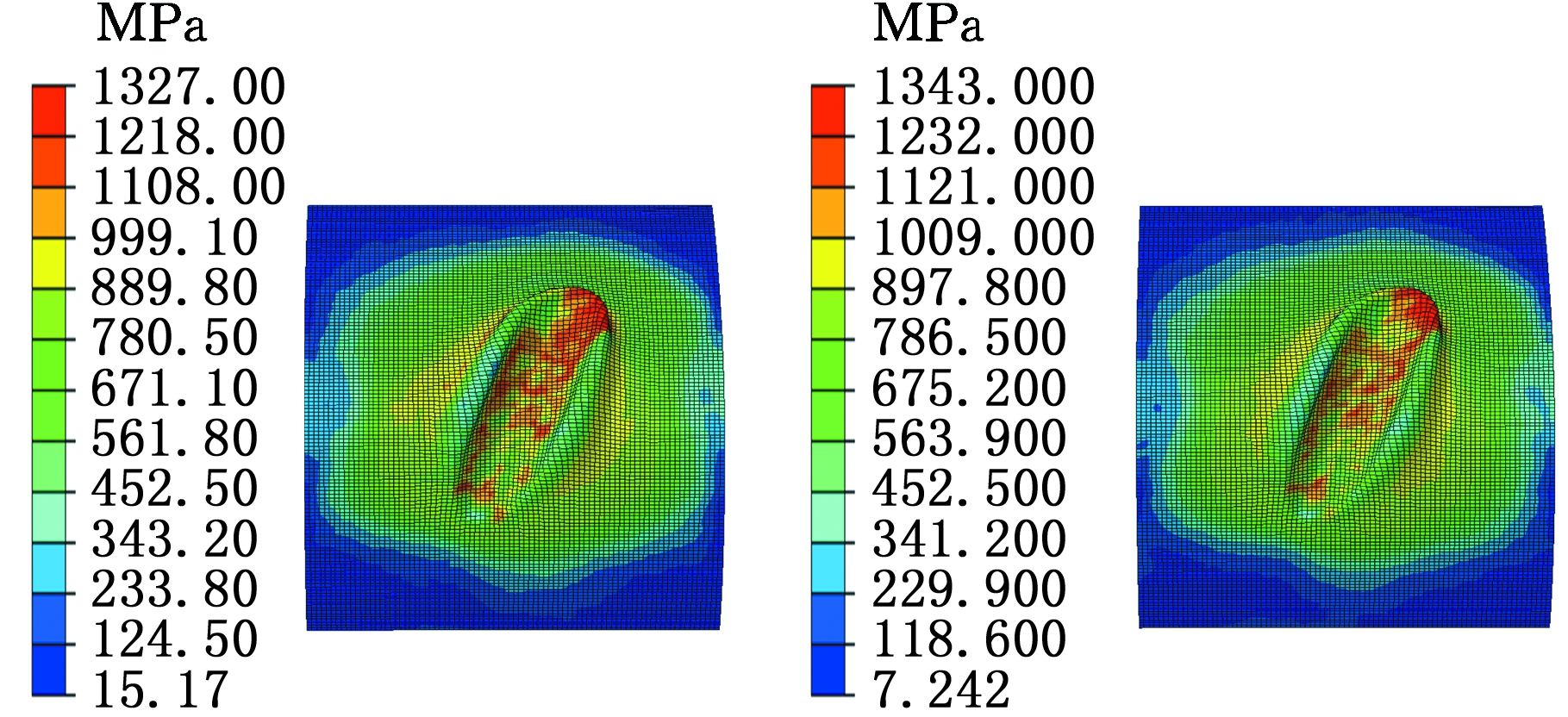
(a)Rs=10 mm (b)Rs=12 mm
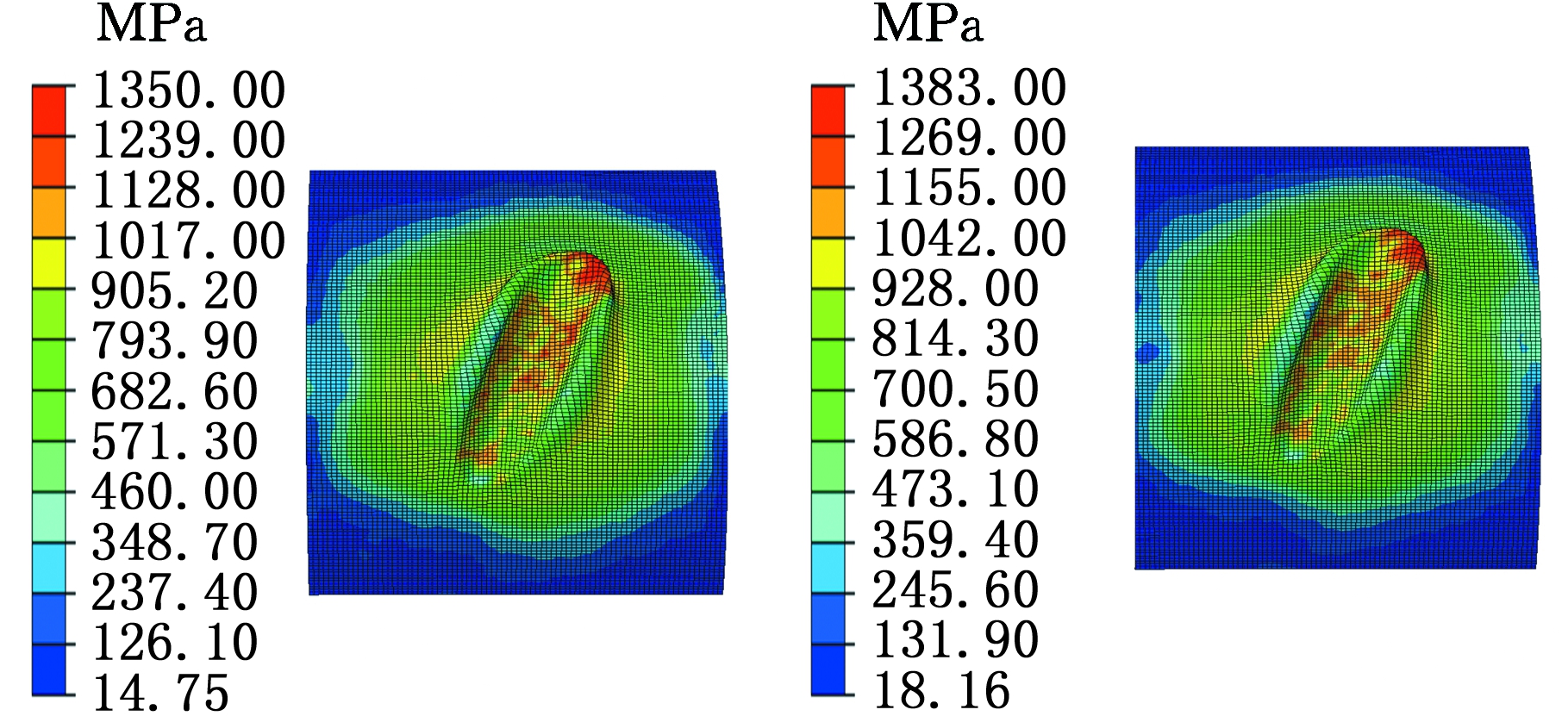
(c)Rs=14 mm (d)Rs=16 mm
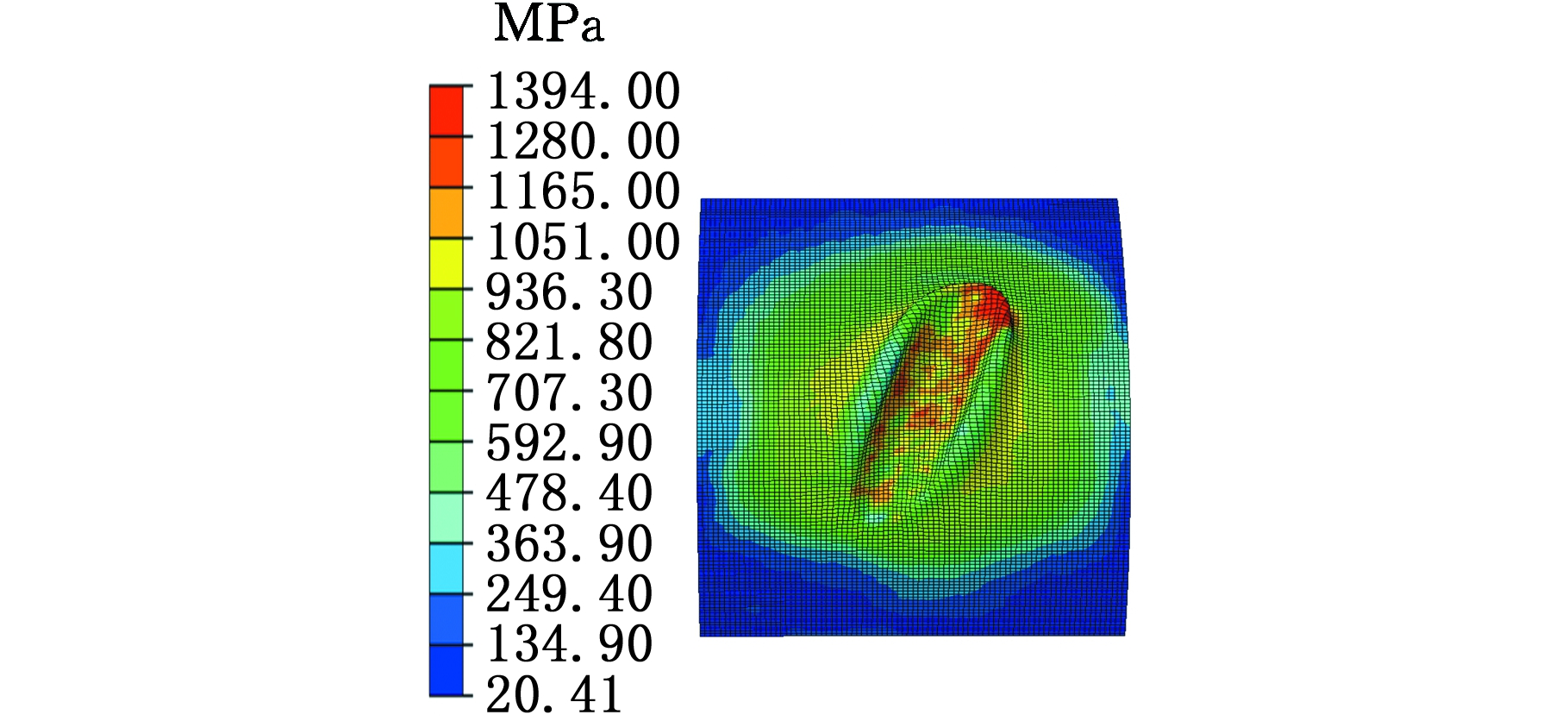
(e)Rs=18 mm
图5 滚打轮半径对Mises应力的影响
Fig.5 The effects of Mise forces on different roller radius
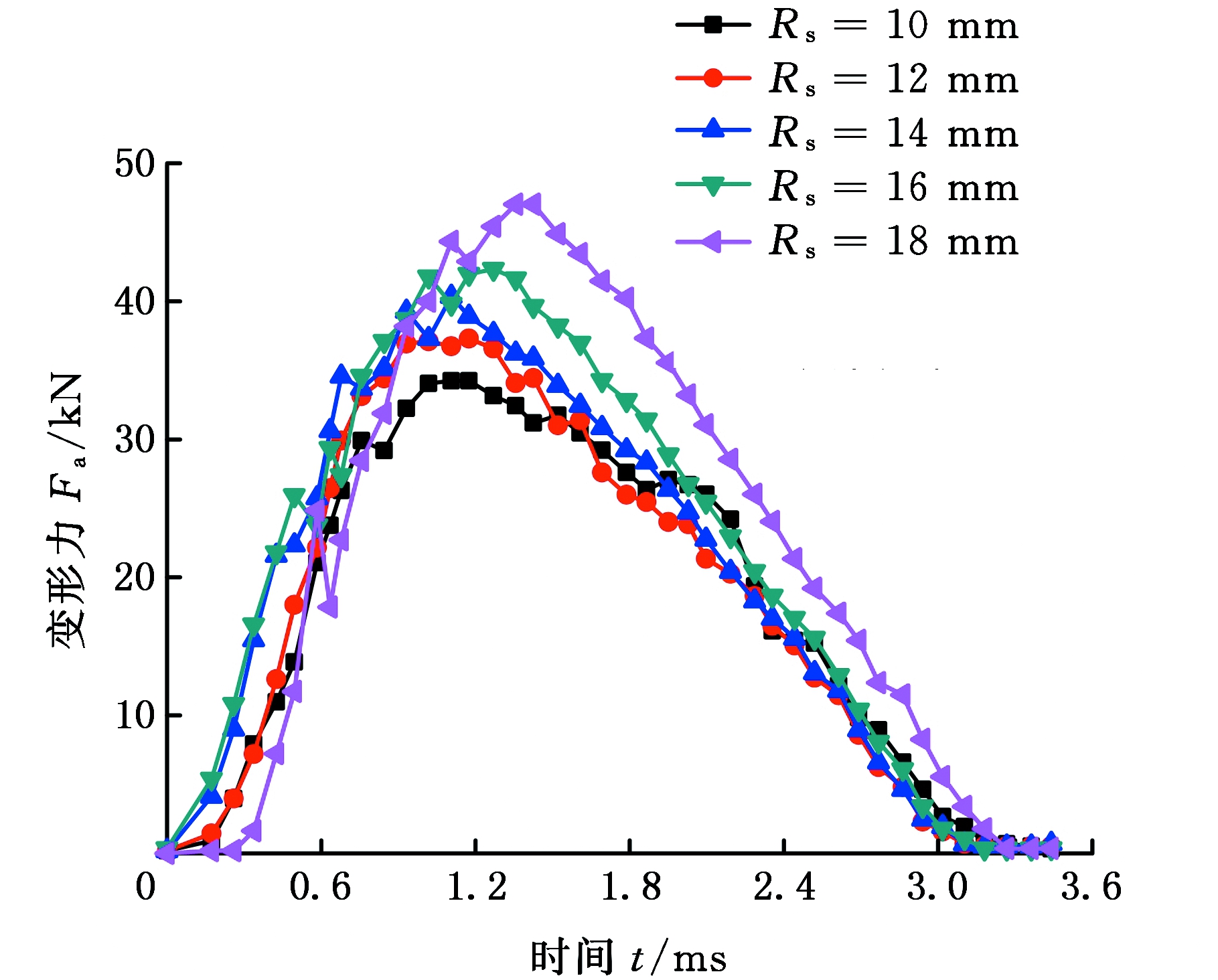
图6 滚打轮半径不同时的变形力
Fig.6 The roller forming forces in different
roller radius
从能量角度来看,随着滚打轮半径的增大,塑性应变能和摩擦耗散能增大,变形体热效应和温度效应增强;塑性应变能增幅较小,滚打轮半径对塑性变形的影响较小;塑性应变能和摩擦耗散能数值上比较接近,摩擦所产生的热量影响较大;弹性应变能的差值增大,弹性回复增加。
3.1.2 滚打轮圆角半径对变形力的影响
在有限元模拟中分别设置5个不同的滚打轮圆角半径,分别为1.5 mm、2 mm、2.5 mm、3 mm、3.5 mm,滚打轮公转速度为1 000 r/min,滚打轮半径为12.25 mm,单次滚打过程切入量为1 mm。图7为滚打轮圆角半径不同时单次滚打过程变形力的变化曲线。

图7 滚打轮圆角半径不同时的变形力
Fig.7 The forming forces when rounded corner of
radius is different
滚打轮圆角半径增大,变形力随之增大,在滚打轮圆角半径增大到3.5 mm时有所下降。滚打轮圆角半径增大,滚打轮与毛坯之间的接触面积改变,变形力随之而变。滚打轮圆角半径改变时,接触面各点处的正应力与切应力的大小及方向均产生变化,对冷滚打成形的影响较复杂。单次滚打过程中接触面积的最大值变化规律性不强,在滚打轮圆角半径为2.5 mm和3.5 mm时反而有所减小。
滚打轮圆角半径变化,接触面正应力及切应力的合力随之变化,进而影响到变形力。单次滚打中接触面上正应力的合力及其分力并没有随着滚打轮圆角半径的增大而单调增大,而在滚打轮圆角半径为2.5 mm和3.5 mm时有所减小。滚打轮圆角半径增大,切应力的合力及其分力的最大值先增大,在滚打轮圆角半径为3.5 mm时减小。
从能量角度来看,滚打轮圆角半径增大时,内能、塑性应变能、弹性应变能的变化较为复杂,规律性不强,摩擦耗散能和弹性应变能的差值总的来说是在增大,但增加的幅度较小。从能量的变化来看,滚打轮圆角半径对冷滚打成形的影响较为复杂。
3.1.3 打入量对变形力的影响
在有限元模拟中分别设置5个不同的打入量,分别为0.5 mm、0.7 mm、0.9 mm、1.1 mm、1.3 mm,滚打轮半径为12.25 mm,滚打轮圆角半径为1.5 mm,滚打轮速度1000 r/min不变。图8为打入量不同时单次滚打过程中变形力的变化曲线。

图8 不同打入量时的变形力
Fig.8 The forming forces of different infeed
由图8可知,随着打入量的增大,单次滚打时变形力的峰值逐渐增大。在冷滚打成形过程中,打入量的改变直接影响着滚打轮作用于工件时的接触面积,打入量增大使得单次滚打成形接触面积的最大值增大,因此单次滚打变形力的最大值也增大。打入量增大时,应变量增大,材料的真实应力因应变硬化而增大,进而使变形力增大。材料加工硬化引起的变形力增大值并没有随着切入量的增大而线性增大,在打入量为1.1 mm时增幅有所减小;在设置不同的打入量时,滚打轮的滚打速度是相同的,同为1 000 r/min,但是,随着打入量的增加,同样时间内应变程度是增大的,即应变率提高,材料的真实应力随着应变率的增大而增大,进而使变形力增大。材料应变率效应引起的变形力增大值也没有随着打入量的增大而线性增大,在打入量为0.9 mm和1.3 mm时增幅有所减小。仿真结果表明,在不同打入量下,材料应变率效应引起的变形力增大值远超过材料应变硬化引起的变形力增大值,材料应变率效应对变形力的影响较大。
从能量角度来看,随着打入量的增大,总的趋势是内能、塑性应变能、摩擦耗散能增大,变形体热效应和温度效应增强。但在打入量为0.7 mm时情况比较特殊,内能、塑性应变能的增幅以及单次成形中打入、打出阶段弹性应变能的差值均为最大。
3.2 变形力仿真的正交试验及结果分析
3.2.1 正交试验设计
据丝杠冷滚打成形的原理,分析不同工艺参数下有限元仿真结果发现,加工工艺参数和成形工具的几何参数等对变形力影响较大。综合考虑丝杠高速冷滚打成形工艺与成形质量,选取滚打轮的打入量、滚打轴转速、滚打轮厚度及工件转速4个因素,每个因素选定为3个水平,设计正交水平表见表3。
表3 正交水平表
Tab.3 Orthogonal test level

水平打入量f(mm)滚打轮厚度tr(mm)滚打轴转速nw(r/min)工件转速nr (r/min)11.5330003021.02.520002030.52100010
由表3,选用L9(34)正交表来安排仿真实验,仿真实验方案及结果如表4所示。仿真过程中设定滚打轮的直径为45 mm,选择的考察指标为径向力、轴向力、切向力。
表4 正交试验表
Tab.4 Table of orthogonal test

实验打入量f(mm)滚轮厚度tr(mm)滚打轴转速nw(r/min)工件转速nr(r/min)径向力(kN)轴向力(kN)切向力(kN)11.533 0003038.9900.4848.52221.52.52 0002031.4320.2616.63831.521 0001023.6460.3824.99841.032 0001028.8740.00414.65751.02.51 0003026.5190.0023.94961.023 0002020.9340.1612.90570.531 0002019.0080.0211.46680.52.53 0001015.1050.01431.06790.522 0003013.1520.02620.873
3.2.2 正交试验结果分析
结果分析可从直观分析和方差分析两方面进行。直观分析是建立正交极差表,计算不同因素的极差,通过极差比较确定对观察指标的影响大小,最终确定最优实验方案。方差分析又称“变异数分析”,是对多个样本均数差别的显著性检验。方差分析从观测变量的方差入手,对偏差平方和(各试验指标与其平均值差的平方和)进行分解,发现观测指标受误差及各种因素变化的影响规律,据此判断各因素对指标影响的显著性。
(1)径向滚压力直观分析。表5给出了径向滚压力直观分析的计算结果。表中,ki(i=1,2,3)表示正交表中相同水平下,每个影响因素对应的指标值之和;![]() 表示对应ki相应水平下所有试验指标的均值;极差R=max kj-min kj(j=1,2,3),反映各个因素对所考察指标影响显著性程度;不同因素对应ki(i=1,2,3)的值越大,说明该因素对应水平越高。
表示对应ki相应水平下所有试验指标的均值;极差R=max kj-min kj(j=1,2,3),反映各个因素对所考察指标影响显著性程度;不同因素对应ki(i=1,2,3)的值越大,说明该因素对应水平越高。
由表5可以看出,对径向滚压力影响最大的因素水平组合为f1tr1nr1nw1(其中f1是打入量f
表5 径向滚压力直观分析表
Tab.5 Visual analysis of radial rolling force

径向滚压力(kN)f(mm)tr(mm)nr(r/min)nw(r/min)k194.06886.87275.02978.661k276.32773.05673.45871.374k347.26557.73269.17367.625k131.35628.95725.01026.220k225.44224.35224.48623.791k315.75519.24423.05822.542R15.6019.7131.9523.679
在k1水平下的值,余类似),影响最小的组合为f3tr3nr3nw3。另外,影响因素的极差值Rf>Rtr>Rnw >Rnr,说明4个考察因素中,打入量的影响最为显著,其次为滚打轮厚度,而工件转速的影响最不显著。可以看出,随打入量、滚打轮厚度、滚打轴转速和工件转速的增大,径向滚压力都呈增大趋势。
(2)径向滚压力方差分析。表6所示为不同影响因素对应的偏差平方和、自由度、均方差及F值,将F值与F分布的临界值进行对比以判断各因素影响的显著性。
表6 径向滚压力方差分析表
Tab.6 Analysis of variance table of radial rolling force

指标方差来源偏差平方和自由度均方差F值显著性径向滚压力(kN)f367.62185.4259.910∗tr141. 5270.82522.884(∗)nw20.69210.3453.343误差E6.1923.095总和T537.398F0.1(2,2)=9,F0.05(2,2)=19,F0.01(2,2)=99
由表6可以得到以下结论:① 因素nw作用不显著,从减小径向滚压力角度出发,可以选择较小的nw。② 因素f的F值F=59.910>F0.05(2,2)=19,说明滚打轮打入量的影响最为显著,随着打入量增加,滚打轮与工件之间的接触面积增大,接触面金属材料产生的塑性流动阻力必然增大,因而导致径向滚压力增大。表5中的结果也验证了这一点。因此考虑工件和滚打轮在实际加工过程中的受力情况,应在保证成形质量前提下,适当考虑渐次增加打入量和滚打次数的加工成形方式。综上,各因素对径向滚压力影响的主次关系是:f→tr→nw→nr。
(3)轴向挤压力直观分析。由表7可知,随滚打轮厚度和滚打轴转速增大,轴向挤压力呈先增大而后减小趋势;伴随打入量增大,轴向挤压力呈现先减小而后增大趋势;随着转速增大轴向挤压力也不断增大。
表7 轴向挤压力直观分析表
Tab.7 Visual analysis of axial extrusion force
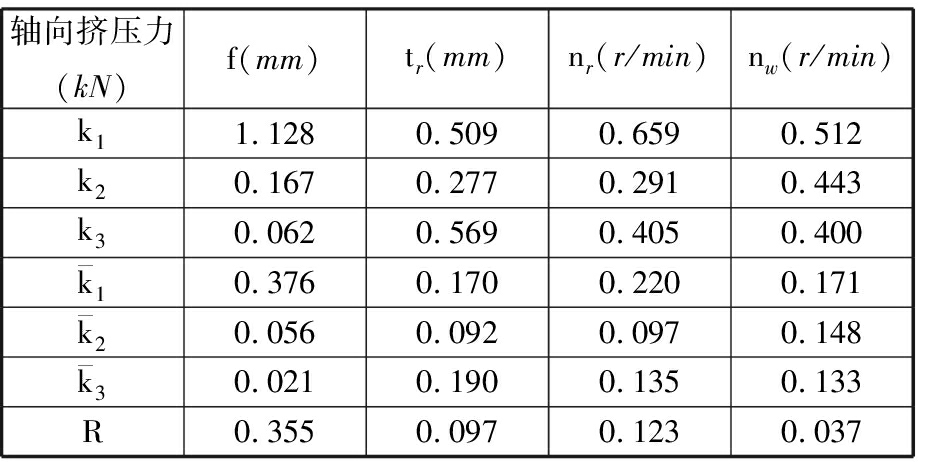
轴向挤压力(kN)f(mm)tr(mm)nr(r/min)nw(r/min)k11.1280.5090.6590.512k20.1670.2770.2910.443k30.0620.5690.4050.400k10.3760.1700.2200.171k20.0560.0920.0970.148k30.0210.1900.1350.133R0.3550.0970.1230.037
(4)轴向挤压力方差分析。由表8可知,因素tr和nr的影响不显著。说明增大滚打轮厚度和滚打轴转速时,轴向挤压力变化较小。综上,4因素对轴向挤压力影响的主次关系是:f→nr→tr→nw。
表8 轴向挤压力方差分析表
Tab.8 Analysis of variance table of radial rolling force
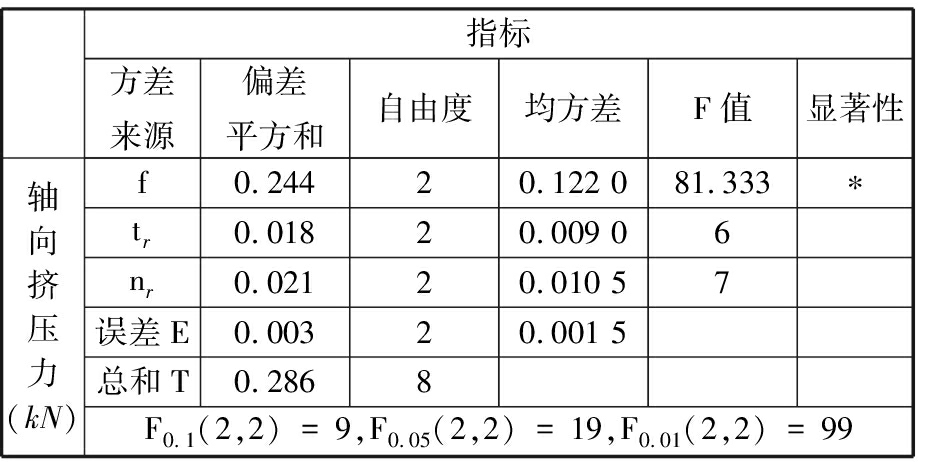
指标方差来源偏差平方和自由度均方差F值显著性轴向挤压力(kN)f0.24420.122 081.333∗tr0.01820.009 06nr0.02120.010 57误差E0.00320.001 5总和T0.2868F0.1(2,2)=9,F0.05(2,2)=19,F0.01(2,2)=99
(5)切向击打力直观分析。由表9可以看出,影响切向击打力最大的水平组合为f1tr1nr1nw1,影响切向击打力最小的组合为f3tr3nr3nw3。影响因素的极差值Rf>Rtr>Rnw >Rnr,滚打轮的打入量对切向击打力的影响最显著,其次是滚打轮厚度和滚打轮转速,而影响最不显著的是工件转速。可以看出,随着打入量、滚打轮厚度、滚打轴转速、工件转速增大,切向击打力均呈逐渐增大的趋势。
表9 切向击打力直观分析表
Tab.9 Visual analysis of tangential impact force
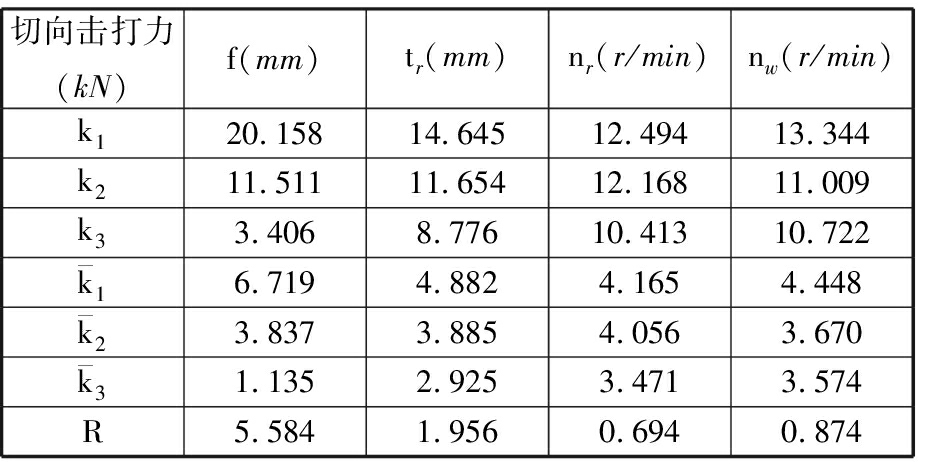
切向击打力(kN)f(mm)tr(mm)nr(r/min)nw(r/min)k120.15814.64512.49413.344k211.51111.65412.16811.009k33.4068.77610.41310.722k16.7194.8824.1654.448k23.8373.8854.0563.670k31.1352.9253.4713.574R5.5841.9560.6940.874
(6)切向击打力方差分析。由表10可知:参考表5的结果,打入量的改变会引起切向击打力较大变化;因素tr和nw影响不显著,增大滚打轮的厚度tr和工件的转速nr对切向击打力的变化影响不大。综上,4因素影响切向力主次关系为:f→tr→nw→nr。
表10 切向击打力方差分析表
Tab.10 Analysis of variance table of
tangential impact force

指标方差来源偏差平方和自由度均方差F值显著性切向击打力(kN)f46.788223.3 94056.034∗tr5.74222.8 7106.877nw1.37920.689 51.651误差E0.83520.417 5总和T54.7448F0.1(2,2)=9,F0.05(2,2)=19,F0.01(2,2)=99
3.3 多次滚打结果分析
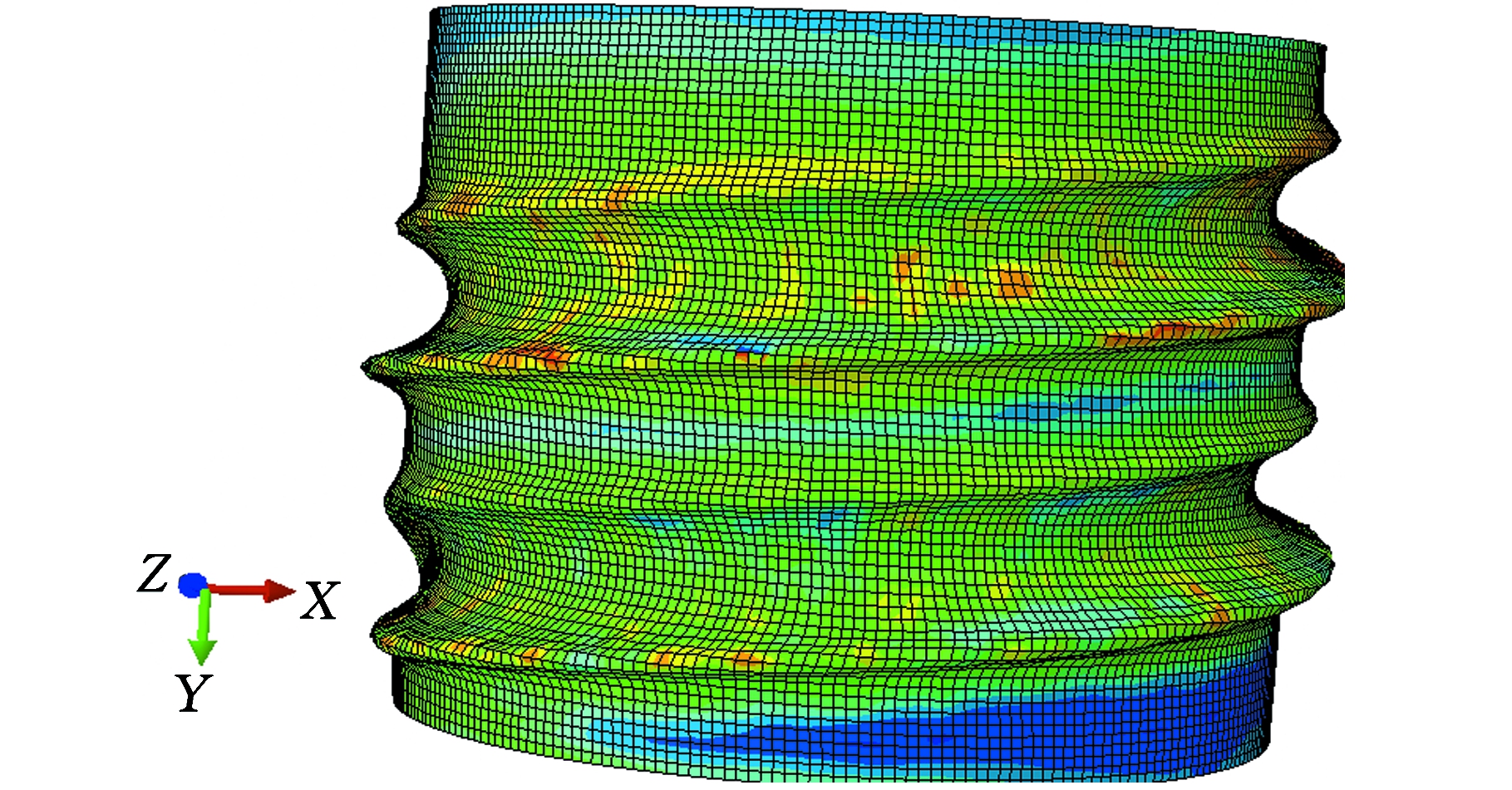
图9 冷滚打成形丝杠形状
Fig.9 Profile under cold roll-beating leadscrew

图10 冷滚打成形过程变形力
Fig.10 The forming force of cold roll-beating
forming process
多次冷滚打成形过程中,设置打入量为1.5 mm,工件转速为60 r/min,沿轴向移动速度为5 mm/s,滚打轮公转速度为1 500 r/min。仿真获得成形丝杠形状如图9所示,变形力如图10所示。可以看出,整个冷滚打过程分为打入、稳定滚打与打出三个阶段。在打入阶段,滚打轮与工件之间的相对位置关系使得滚打轮与工件之间的接触面积比较小,变形力也较小。随着滚打轮的不断打入,滚打轮与工件之间的接触面积不断增大,从而使得滚打变形力逐渐增大,直到进入稳定滚打区。在打出阶段,由于工件的进给运动,滚打轮逐渐远离工件表面,二者之间的接触面积不断减小,故变形力也逐渐变小,直到完全脱离,变形力变为零。冷滚打成形整个过程的变形力变化趋势是先增大,然后进入平稳滚打期,最后逐渐减小为零的。
4 实验
本次丝杠冷滚打实验在普通车床上进行,如图11所示。滚打轴安装在焊接的U形支架上,电机通过一级齿形同步带传动驱动滚打轮转动,用变频器调节滚打轮的转速;试件用三爪卡盘和顶尖来装夹,用车床主轴带动试件旋转;进给运动用车床的进给箱和丝杠系统来实现。

图11 实验设备图
Fig.11 The photo of expriment equipment
为了验证冷滚打滚珠丝杠运动学分析和数值模拟的正确性,进行冷滚打成形丝杠实验,实验参数与多次滚打仿真参数相同,获得成形丝杠如图12所示,成形过程中滚打力的变化曲线见图13,其与仿真获得冷滚打成形过程变形力的变化规律基本相似,说明了有限元仿真模型的正确性。

图12 实验加工的丝杠
Fig.12 Experimental leadscrew

图13 冷滚打成形过程受力图
Fig.13 Force diagram of cold roll-beating
forming process
在冷滚打成形过程中,滚打变形力的变化情况具有一定的波动,且有规律地出现波峰与波谷。由于滚打成形运动是一个具有高速冲击作用的运动过程,在滚打轮的高速冲击作用下,不可避免地会产生振动,当振动频率接近工件系统的固有频率时,引起工件的共振,此时振幅达到最大,并出现力的最大值,即变形力曲线图(图13)中的波峰。冷滚打成形是一个周期性的加载-卸载过程,所以波峰与波谷的出现呈规律性。
平稳阶段单次滚打过程中的受力情况如图14所示。可以看出,冷滚打成形过程是单次滚打的周期性重复过程,说明冷滚打塑性成形是一个局部加载、多次击打工件逐步累积成形的过程。高速冷滚打过程中的径向滚打变形力随着时间不断变化,总体上可分为上升(加载)与下降(卸载)两个阶段。上升初始阶段平均斜率较小,变形力较小,这是因为滚打轮与工件第一次接触,需要克服塑性变形抗力,受到的阻力较大,相对变形缓慢;下降阶段曲线较陡,变形较快,是因为二者接触区是已击打区,使变形区发生塑性流动的力小于首次击打力,变形相对容易,但上升与下降阶段基本一致,平稳滚打期单次冷滚打过程中变形力的最大值约为65 kN。滚打过程中滚打轮和工件碰撞的速度较快,二者的接触时间较短。接触碰撞所用的时间只占击打一次时间的小部分,可以近似地认为丝杠单次冷滚打过程是一个瞬时动态加载的过程。单次击打时成形力加载-卸载过程中实验值与仿真值整体变化趋势相同,加载阶段的差异主要是由机床刚度等因素造成的,而卸载阶段实验值与仿真结果变化趋势保持一致。

图14 平稳阶段单次冷滚打变形力曲线
Fig.14 Single cold roll-beating deformation force
curve in stationary stage
5 结论
(1)根据丝杠冷滚打成形的基本原理,应用ABAQUS软件建立了丝杠冷滚打成形的有限元仿真模型;通过单次滚打成形仿真发现,滚打轮半径、滚打轮圆角半径和打入量增大时,Mises应力增大,变形力随之增大。通过多次冷滚打成形仿真,获得了冷滚打成形过程中的变形力的变化规律与成形丝杠的形状。
(2)设计了正交试验,获得了打入量f、滚打轴转速nw、滚打轮厚度tr及工件转速nr4个因素对径向滚压力影响的主次顺序为:f→tr→nw→nr,对轴向挤压力影响的主次顺序为:f→nr→tr→nw,对切向力影响的主次顺序为:f→tr→nw→nr。
(3)在自行设计的丝杠冷滚打设备上实验,获得了多次与单次冷滚打成形丝杠时变形力的变化规律,与仿真获得丝杠冷滚打成形时变形力的变化规律基本相似,验证了丝杠冷滚打成形模型的正确性,为丝杠冷滚打成形力影响因素的研究提供了借鉴。
[1] 华林, 钱东升. 轴承环轧制成形理论和技术 [J]. 机械工程学报, 2014, 50(16): 70-76.
HUA Lin, QIAN Dongsheng. Ring Rolling Forming Theory and Technology for Bearing[J]. Journal of Mechanical Engineering, 2014, 50(16): 70-76.
[2] HE Wangyun, LI Yan, YANG Mingshun, et al. Forming Flaws Analysis of Lead Screw Cold Roll-beating Based on Stress-strain Evolution [J]. Sensors & Transducers, 2013, 17(1): 74-82.
[3] PENG L F , XU Z T , FU M W , et al. Forming Limit of Sheet Metals in Meso-scale Plastic Forming by Using Different Failure Criteria [J]. International Journal of Mechanical Sciences, 2017, 120: 190-203.
[4] ABDULLAH L, JAMALUDIN Z, MASLAN M N, et al. Assessment on Tracking Performance of Cascade P/PI, NPID and NCasFF Controller for Precise Positioning of XY Table Ballscrew Drive System [J]. Procedia CIRP, 2015, 26(1): 212-216.
[5] LIU Z Y , DONG C Y . Automatic Coupling of ABAQUS and a Boundary Element Code for Dynamic Elastoplastic Problems [J]. Engineering Analysis with Boundary Elements, 2016, 65: 147-158.
[6] 张璐, 杨明顺, 李言, 等. 高速冷滚打过程变形力解析方法及其修正 [J]. 塑性工程学报, 2011, 18(5): 1-7.
ZHANG Lu, YANG Mingshun, LI Yan, et al. Analytic Method and Its Modification for Deformation Force of Highr Speed Cold Roll-beating Forming[J]. Journal of Plasticity Engineering, 2011, 18(5): 1-7.
[7] 张璐, 李言, 杨明顺, 等. 丝杠冷滚打成形过程金属流动规律研究 [J]. 中国机械工程, 2012, 23(13): 1623-1628.
ZHANG Lu, LI Yan, YANG Mingshun,et al. Study on Metal Flowing of Lead Screw Cold Roll-beating Forming[J].China Mechanical Engineering, 2012, 23(13): 1623-1628.
[8] 崔凤奎, 徐永福, 赵魏. 花键冷滚打和铣削加工的金属组织变形研究 [J]. 锻压技术, 2008, 33(2): 70-74.
CUI Fengkui, XU Yongfu, ZHAO Wei. Research on Metal Microstructure Deformation of Splines Manufactured by Cold Rolling Milling and Cutting Processes[J]. Forging&Stamping Technology, 2008, 33(2): 70-74.
[9] 崔凤奎, 谢亚飞, 董晓丹, 等. 高速冷滚打成形金属流动仿真分析 [J]. 河南理工大学学报(自然科学版), 2014, 33(4): 467-471.
CUI Fengkui, XIE Yafei, DONG Xiaodan, et al. Simulation Analysis of Metal Flow in High-speed Cold Roll-beating[J]. Journal of Henan Polytechnic University (Natural and Science), 2014, 33(4): 467-471.
[10] 崔凤奎, 李言, 周彦伟, 等. 渐开线花键滚轧轮建模及其修正 [J].南京航空航天大学学报,2005,37(增刊1):90-93.
CUI Fengkui, LI Yan, ZHOU Yanwei, et al. Modeling and Modification of Involute Spline Rolling Wheel[J]. Journal of Nanjing University of Aeronautics & Astronautics,2005,37(S1):90-93.
[11] 崔凤奎, 李言, 李春梅. 渐开线花键加工方法进展 [J]. 矿山机械, 2007, 35(2): 116-119.
CUI Fengkui, LI Yan, LI Chunmei. The Development of Involute Spline Machining Method[J]. Mining & Processing Equipment, 2007, 35(2): 116-119.
[12] 张璐, 李言, 杨明顺, 等. 高速冷滚打成形过程的有限元数值模拟 [J]. 机械工程材料, 2012, 36(8): 86-88.
ZHANG Lu, LI Yan, YANG Mingshun, et al. Finite Element Numerical Simulation for High Speed Cold Roll Beating Forming Process[J]. Materials for Mechanical Engineering, 2012, 36(8): 86-88.
[13] 李玉玺, 李言, 杨明顺, 等. 40Cr高速冷滚打成形过程模拟分析 [J]. 机械科学与技术, 2016, 35(4): 594-600.
LI Yuxi, LI Yan, YANG Mingshun, et al. Simulation Analysis for High Speed Cold Roll Beating Forming Process of 40Cr Steel[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(4): 594-600.
