0 引言
电池荷电状态(state of charge,SOC)作为电池管理系统(BMS)的重要指标,其精确估计对保障电池组安全性和续航能力有重要意义。然而SOC作为电池内部不可直接测量的状态量,它的测量需通过其他各类方法间接获取。
安时积分法[1]作为常见的SOC估计方法易于实现,但是准确的初始SOC值难获取,且易受到噪声的干扰产生累计误差,通常需要和其他方法结合使用。开路电压法[2]测量简单,但是需要对电池进行长时间的静置,实用性差。另一类方法是基于模型的SOC观测器法。常用的电池模型有电化学模型[3]、电热模型、等效电路模型[4](equivalent circuit model, ECM)和智能计算模型,其中ECM因其精度高、计算量小等特点而常与其他各类自适应滤波器结合使用。常见的滤波方法有扩展卡尔曼滤波器(extended Kalman filter, EKF)及其变体[5]、无迹卡尔曼滤波(unscented Kalman filter, UKF)及其变体[6]、粒子滤波器[7]、龙贝格观测器[8]和H∞观测器。这类方法的共同的缺点是只能离线参数辨识,无法实现参数实时更新。
文献[9]使用了递推最小二乘(RLS)法在线更新电池模型参数,同时采用观测器法估计SOC。该方法虽然能取得较好的估算精度,但是只适用于仅有输出噪声的情况,实用性差。文献[10]使用了双卡尔曼滤波算法,能够实现参数的在线更新,但文中采用了对模型精度要求较高的EKF进行SOC估计,并且未考虑噪声对模型参数的影响。文献[11]虽然考虑了噪声对模型精度的影响,但没能提出模型参数在线更新的方法,进而在实际应用中不能很好地反映电池的实际状态。
针对以上问题,本文提出了基于Frisch 方案[12-13]的双滤波(英文全称FSDF)算法。文中首先考虑锂电池中开路电压和SOC之间的迟滞效应的影响,将Preisach模型和一阶RC模型结合建立新的电池模型,随后证明噪声会导致模型参数辨识出现偏差。为了减小噪声的影响,采用了Frisch 方案对充放电电流和端电压的噪声方差进行估计,从而得到噪声含量较少的电流和端电压,随后采用EKF结合UKF进行模型参数的实时更新和单体电池SOC的在线估算。
1 电池模型的建立
1.1 Preisach离散模型
Preisach模型(PM)是一种广泛使用的表征迟滞效应的工具。该模型被构造为由无限个简单的迟滞算子γαβ(α和β分别表示上阈值和下阈值)叠加而成。为了表示锂电池开路电压与电池荷电状态(OCV-SOC)非线性滞回关系,采用Preisach模型将其描述为
UOC(t)=∬α≥βξ(α,β)γαβS(t)dαdβ
(1)
其中,UOC(t)和S(t)分别为t时刻的开路电压和SOC值,ξ(α,β)为权重函数。以α为横轴、β为纵轴建立坐标系。在式(1)中,当SOC发生变化时,在平面α≥β中的每个点(α,β)对应的γαβ将在±1之间切换。
由于输入范围通常是有限的,因此只需将以直线α、β和α=β 3条线组成的直角三角形作为Preisach平面,如图1所示。将三角形的直角边等分为相同的n个部分,则三角形被分为N=n(n+1)/2(N=15,n=5)个正方形Ak,k=1,2,…,N。每个方块可以表示为
Ai(i-1)/2+j={(α,β)|βj≤β<βj+1,αi≤α<αi+1}
(2)
其中,j≤i;i,j=1,2,…,n。假设每个Ak的权重函数ξk为常数,将式(1)离散化可得
(3)

图1 离散Preisach算子方案
Fig.1 Scheme of discrete Preisach operator
令迟滞状态为εk,εk可以表示为
εk(t)=∬Si(i-1)/2+jγαβS(t)dβdα
基于以上分析,式(3)可以表示为
UOC(t)=εT(t)ξ
(4)
ε(t)=(ε1(t),ε2(t),…,εN(t))T ξ=(ξ1,ξ2,…,ξN)T
其中,ξ和ε(t)为有相同维度的权向量。向量ε(t)由滞后曲线中对应时间点为t时刻的输入来确定。ξ由计算机离线求解函数得到。
1.2 一阶RC模型结合Preisach离散模型
一阶RC模型如图2所示。其中,UOC为电池开路电压,R0为欧姆内阻,C1为极化电容,R1为极化电阻,IL为放电电流,图中方向为正,Ut为开路电压。

图2 一阶RC模型
Fig.2 First-order RC model
当电池放电时,根据基尔霍夫电压电流定律结合式(4)得

(5)
时间常数τ(t)=R1(t)C1(t),根据式(5)可得
(6)
2 输入输出噪声方差估计
假设电池模型组成系统的传递函数为
其中,A(q-1)=1+a1q-1+…+anaq-na,B(q-1)=b1q-1+…+bnbq-nb。在电池模型中,输入电流IL和输出端电压Ut都是含噪声的量,假设这些噪声均为加性噪声,则可表示如下:
(7)
其中![]() 和
和![]() 分别为输出Ut0,k和输入IL0,k的噪声;Ut,k和IL,k分别为无噪声输出和输入。假设
分别为输出Ut0,k和输入IL0,k的噪声;Ut,k和IL,k分别为无噪声输出和输入。假设![]() 和
和![]() 为高斯白噪声,其均值为0,方差分别为σU和σI。
为高斯白噪声,其均值为0,方差分别为σU和σI。
令φu0,k=(IL0,k,IL0,k-1)T,φy0,k=(-Ut0,k-1)T,![]()
定义任意两个向量p和q,p的自协方差矩阵以及p和q的协方差矩阵分别为
Σp=E(ppT) Σpq=E(pqT)
向量p和一个随机变量r的协方差矩阵为
Γpr=E(pr)
由于输入输出中的噪声均为高斯白噪声,故![]() 其中
其中![]()
为了求解σU和σI,采用了Frisch方案对向量φ0k进行如下处理。
根据Frisch方案可得
(8)
其中,λmin(F(k))为F(k)的最小特征值;Inb为2阶单位矩阵。
令
(9)
定义
δ=(a1,a2,…,ana,b1,b2,…,bnb)T
其中![]() 和
和![]() 分别为A(q-1)和B(q-1)的估计。则
分别为A(q-1)和B(q-1)的估计。则![]() 的样本协方差为
的样本协方差为
(10)
令
(11)
其中,![]() 为t时刻端电压噪声的估计;
为t时刻端电压噪声的估计;![]() 为负载电流的噪声估计。将Σμ和Σμ0进行比较,令
为负载电流的噪声估计。将Σμ和Σμ0进行比较,令
VN(σI)=ψTMψ
(12)
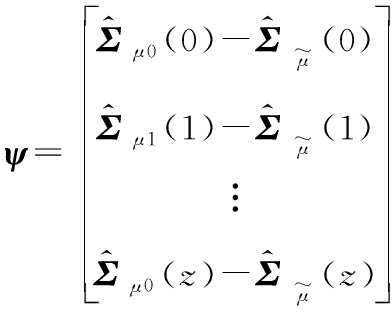

其中,ψ为残差向量;M为正定权重矩阵;z可以根据实际需求选取。
根据式(12)可以得出![]() 的解:
的解:
(13)
根据式(9)和式(13)可求出电流和端电压的噪声协方差,再根据式(7)可求得滤除噪声的电流和端电压。
3 参数辨识和SOC估计
3.1 模型初始参数辨识
为了得到模型的初始参数,参考了《Freedom CAR 功率辅助型电池测试手册》对锂电池进行HPPC测试实验。在室温条件下,以1 C(电池额定容量大小的电流对电池放电1 h)放电电流放电5 min,然后静置10 min,再以同样的电流充电5 min,充放电设备记录锂电池端电压和电池表面温度,一个周期的电流和电压曲线如图3所示,其中U1,U2,…,U5为电池的5个充放电瞬间的电压,根据分析可得
(14)
(15)
(16)
式中,U4、U5分别为t4、t5时刻的端电压。

图3 HPPC实验电压电流波形
Fig.3 HPPC experimental voltage and current waveforms
3.2 双卡尔曼滤波进行参数更新和SOC估计
根据SOC的定义,得出SOC值的表达式:
(17)
式中,S0为初始SOC值;η为充放电效率,η≤1;CN为电池的额定容量;i(t)为电池的实际电流,充电时,i(t)<0;放电时,i(t)>0。
为了应用卡尔曼滤波,将式(17)离散化得
(18)
结合式(5)、式(6)、式(17)可得电池模型的离散空间状态方程和输出方程:

(19)

其中,ωk、πk、vk为相互独立的高斯白噪声。
根据式(19)可得如下方程:
(20)
双滤波算法具体过程如下。初始化:
(21)
(1)参数更新过程。EKF时间更新:
(22)
(2)UKF进行SOC估计过程。
①产生k-1时刻的样本sigma点:
(23)
其中,b为电池状态变量的维数,b=2。ζ=α2(n+λ)-n,α=0.8,λ=0,β=2。
②权重计算:

(24)
③时间更新。计算k时刻系统状态的先验估计和先验估计误差协方差:

(25)
④量测更新。计算k时刻的量测估计的预测值和误差协方差:

(26)
⑤先验估计![]() 和量测估计
和量测估计![]() 的协方差以及UKF增益更新:
的协方差以及UKF增益更新:

(27)
⑥电池模型状态和误差协方差后验估计:
(28)
(3)通过先验估计对EKF量测更新:
(29)
(4)参数更新:
(30)
3.3 算法流程图
根据以上的内容,可得出双滤波算法的框图,如图4所示。

图4 FSDF框图
Fig.4 FSDF block diagram
4 实验验证与分析
4.1 实验设计
为了验证本文中算法的有效性,对12节标称容量为20 A·h、额定电压为3.2 V的锂电池串联成的电池组进行UDDS工况测试,图5为测试电流曲线。在25 ℃的条件进行一次循环放电,放电时间为1 500 s,采样间隔为1 s。单体锂电池的初始参数如表1所示。
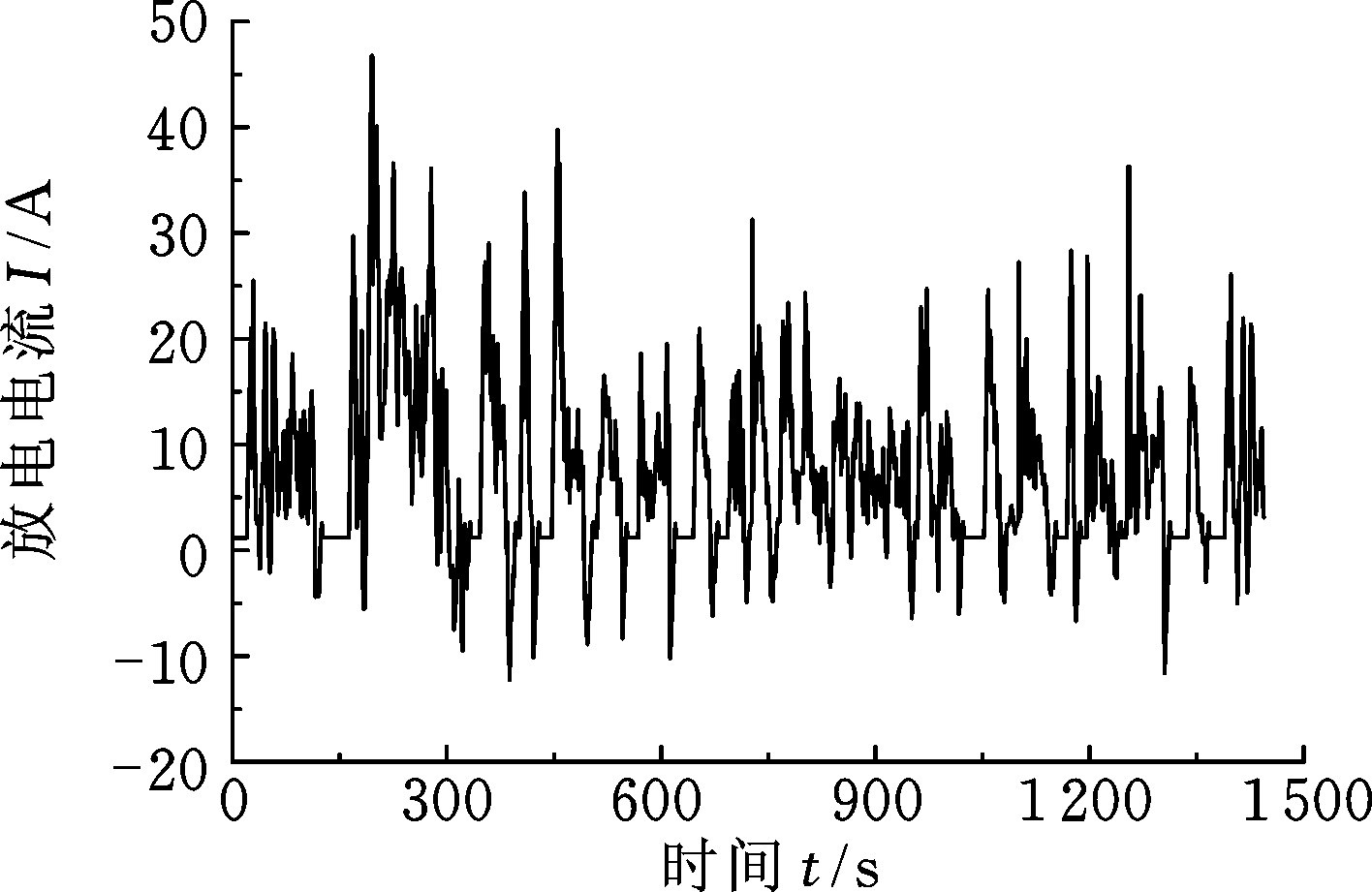
图5 放电电流曲线
Fig.5 discharge current curve
表1 初始参数
Tab.1 Initial parameters
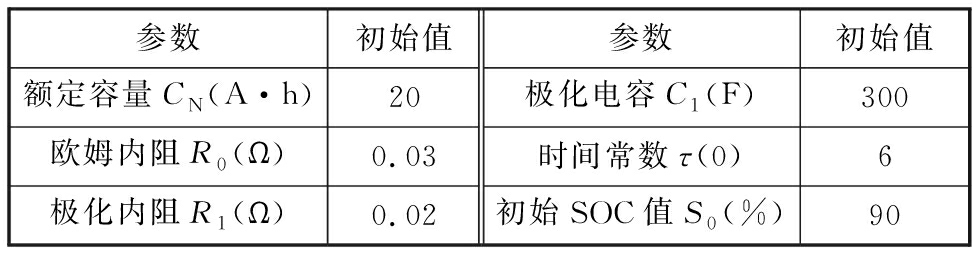
参数初始值参数初始值额定容量CN(A·h)20极化电容C1(F)300欧姆内阻R0(Ω)0.03时间常数τ(0)6极化内阻R1(Ω)0.02初始SOC值S0(%)90
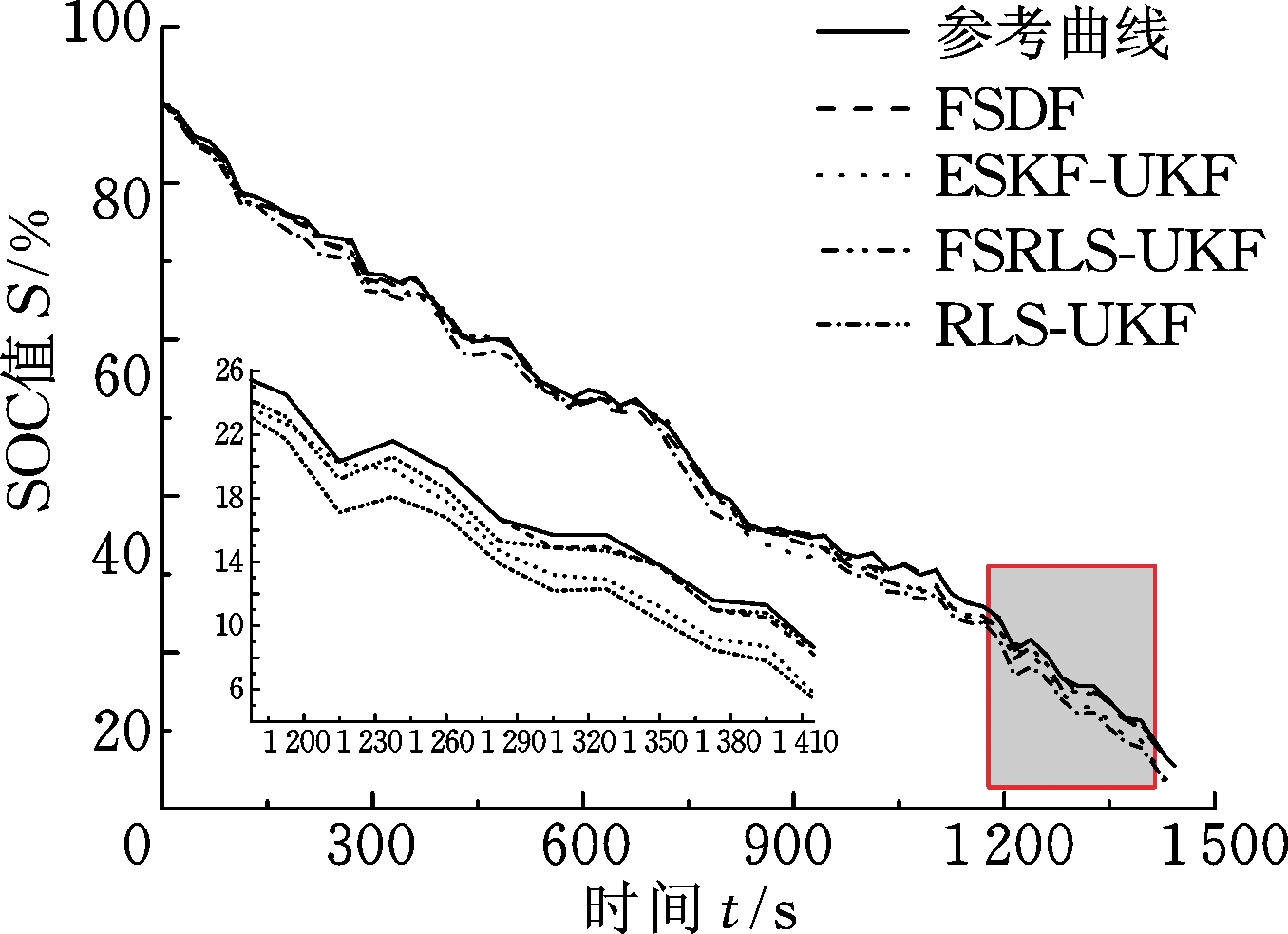
图6 SOC估计曲线
Fig.6 SOC estimation curve
4.2 实验结果分析
实验选择将估算精度较高的安时积分法所得SOC值做为参考值。首先将电池进行充分静置,然后测其开路电压(OCV),再根据SOC-OCV曲线得出SOC值,并将其作为初始SOC值。然后使用BTS-48 V/50 A电池循环寿命测试仪将图5所示的电流曲线加载到电池组上,其电流电压传感器的测量范围为0~50 A和0~48 V,而测量精度在±0.1%以内。另外为了验证算法的可行性,将EKF-UKF方法去噪声前的信号和RLS-UKF算法去噪声前后的信号在相同的实验条件下与本文算法结果对比。SOC变化曲线如图6所示。从图中可以得出,本文双滤波算法FSDF和参考值相比有一定的偏差,但是最大偏差小于2%,最大偏差出现在SOC为45%~55%之间。主要原因在于端电压的测量有一定的误差,并且在此区间OCV随SOC变化很小。而Frisch 方案RLS-UKF(FSRLS-UKF)方法开始具有较好的估算精度,但是在900~1 200 s内偏差达到2.5%,主要原因也是OCV和SOC的相关性小,且算法性能不及FSDF算法。而未去噪声的EKF-UKF信号和RLS-UKF信号则始终都有一定偏差,而且在1 200~1 500 s之间基本偏离了参考值,主要原因是噪声对参数辨识和SOC估计的影响。
为了评估算法的性能,做如下定义:
误差偏差
(31)
误差方差
(32)
误差极差
(33)
图7所示为4种算法的误差方差Gk,从图中可以得出FSDF算法的Gk最小,表明FSDF算法相对于参考值的波动最小,而FSRLS-UKF算法次之,而RLS-UKF算法的Gk最大。通过对比分析得出:①噪声对SOC的估计影响较大,不容忽视,进而证明采用Frisch 方案减少噪声影响的必要性;②EKF-UKF算法较RLS-UKF算法具有更高的估算精度,说明EKF-UKF算法性能优于RLS-UKF算法。表2中给出了4种算法的Gk和G∞的最大值,对这4种算法的性能进行评估得出FDKF估算方法的性能优于其他3种方法。
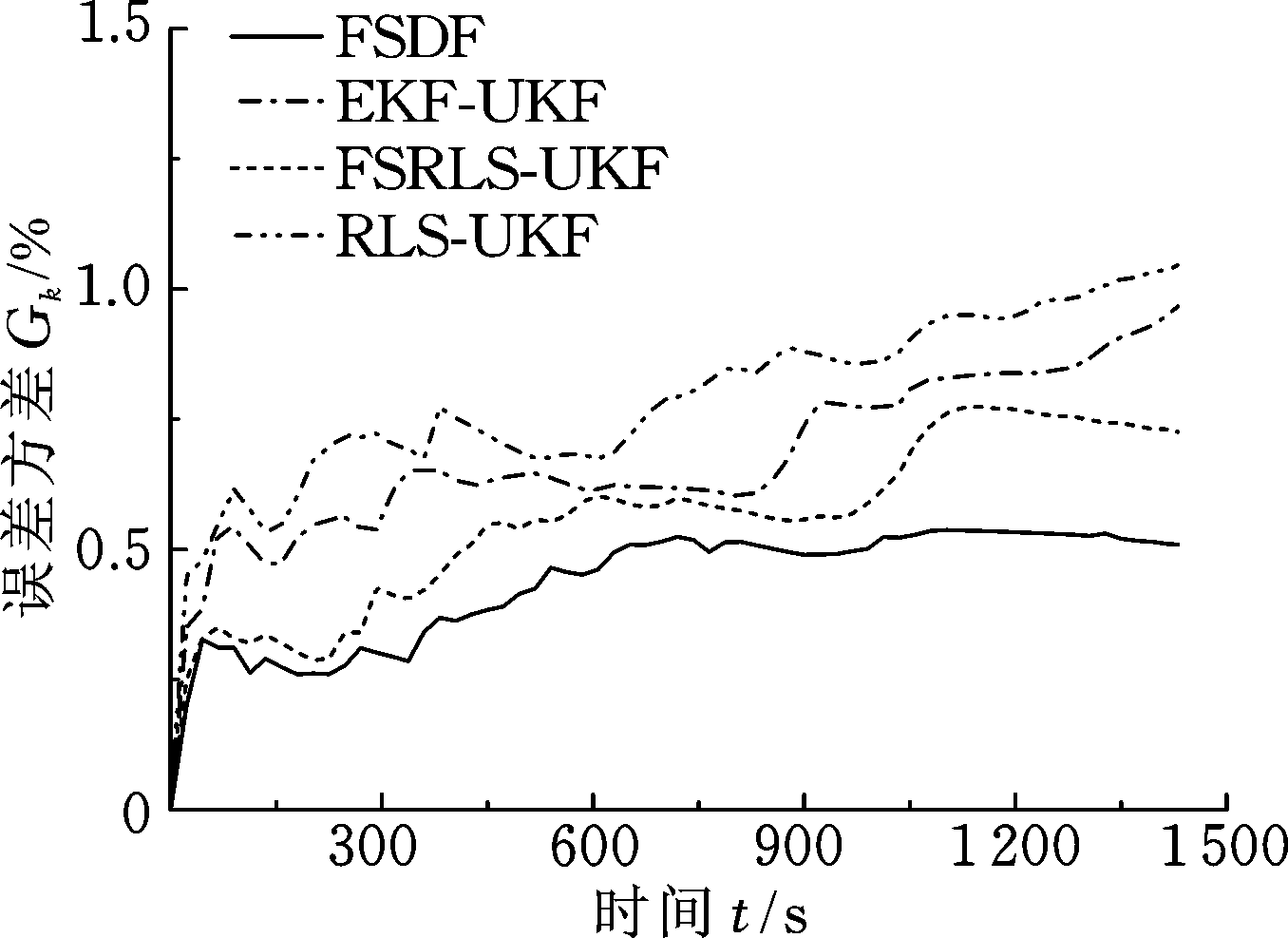
图7 SOC误差方差变化曲线
Fig.7 SOC error variance curve
表2 不同估计方法的性能对照
Tab.2 Comparison of performances of different estimation methods

FSDFEKF-UKFFSRLS-UKFRLS-UKFGk(%)0.536 8090.966 9150.773 9381.045 706G∞(%)1.72.92.53.5
图8所示为FSDF方法对电池模型参数的辨识结果,为了验证噪声对模型精度的影响,本文采用去噪声前的EKF-UKF方法的辨识结果和去噪声后的辨识结果进行对比。参考值的获取通过如下方式:①选取特定的时间点,对放电电流和端电压进行测量;②根据每个时间点电流阶跃变化时电压跳变计算出欧姆内阻R0(式(14));③根据电流阶跃变化时电压的迟滞变化计算出极化内阻R1和极化电容C1(式(15)、式(16))。

(a) 欧姆内阻辨识曲线

(b) 极化内阻辨识曲线
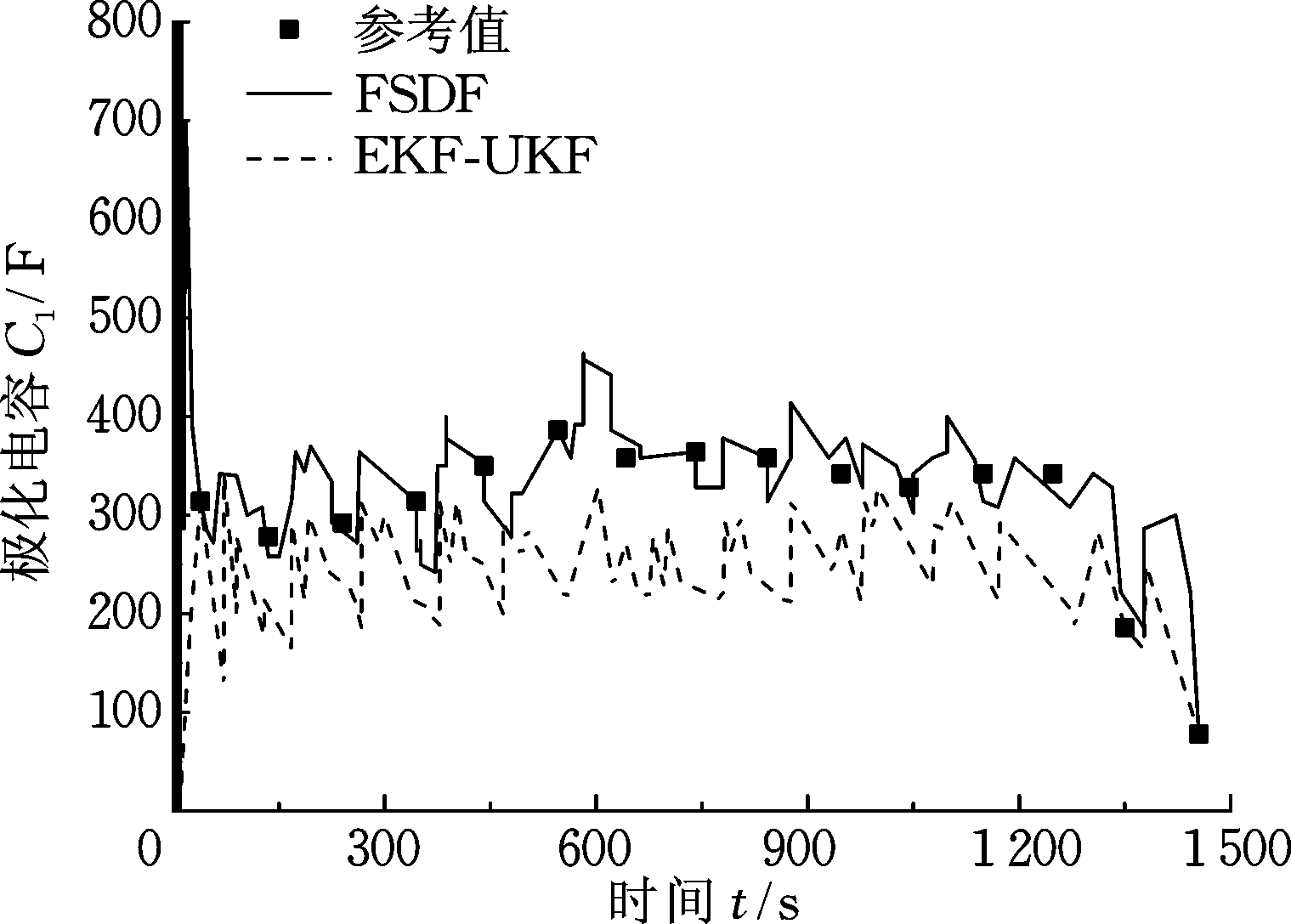
(c) 极化电容辨识曲线
图8 参数辨识结果
Fig.8 Parameter identification results
根据实验曲线分析可得:①虽然噪声对欧姆内阻的影响较小,但是对极化内阻和极化电容的影响较大,因而它对模型的影响不容忽视;②电池内部的参数都是随时间实时变化的,那些采用固定电池模型的SOC估算算法很难达到理想SOC估计精度;③由于RC网络在充电和放电过程中更依赖于电池的化学反应,所以R1和C1的变化比R0更不规则。
5 结论
本文为考虑开路电压和SOC之间的迟滞效应的影响,将一阶RC模型和Preisach模型进行组合得到新的电池模型;为减小噪声对模型参数和SOC估算精度的影响,采用Frisch 方案对模型中的输入输出进行噪声方差估算,从而得到了含噪声较少的输入输出,进而得到精度较高的状态方程和观测方程。随后采用了双滤波法进行参数辨识和SOC在线联合估计。为了验证该算法,将本文提出的算法分别与EKF-UKF、FSRLS-UKF和RLS-UKF算法进行对比,通过实验验证得出,该算法在估算精度上与参考值的最大偏差为1.7%,较FSRLS-UKF算法提高了0.8%,而较RLS-UKF算法提高了1.8%。因此该算法行之有效。
下一阶段将继续本文提出的算法研究。该算法在SOC估计时,虽然能取得不错的精度,但是计算过程较为复杂,因此需要对算法做进一步优化,在保证精度的同时降低算法复杂度。另外,本文的算法只是研究单体电池在常温下的SOC估计,而电池在放电过程中电池内部温度会升高,为了使算法的实用性更强,接下来将会把温度做为影响因素加入算法中,以提高算法的实际应用能力。
[1] 于海芳,逯仁贵,朱春波,等.基于安时法的镍氢电池SOC估计误差校正[J].电工技术学报,2012,27(6):12-18.
YU Haifang, LU Rengui, ZHU Chunbo, et al. State of Charge Estimation Calibration for Ni-MH Battery Based on Ampere-hour Method[J]. Transactions of China Electrotechnical Society, 2012,27(6):12-18.
[2] XING Y J, HE W,PECHT M, et al. State of Charge Estimation of Lithium-ion Batteries Using the Open-circuit Voltage at Various Ambient Temperatures[J]. Applied Energy, 2014,113(1): 106-115.
[3] WEI Z, ZHAO J, SKYLLAS-KAZACOS M et al. Dynamic Thermal-Hydraulic Modeling and Stack Flow Pattern Analysis for All-vanadium Redox Flow Battery[J]. Journal of Power Sources, 2014,260: 89-99.
[4] CHENG X M, YAO L G,PECHT M. Lithium-ion Battery State-of-charge Estimation Based on Deconstructed Equivalent Circuit at Different Open-circuit Voltage Relaxation Times[J]. Journal of Zhejiang University: Science A (Applied Physics & Engineering),2017,18(4):256-267.
[5] 刘征宇,汤伟,王雪松,等.基于双时间尺度扩张卡尔曼粒子滤波算法的电池组单体荷电状态估计[J].中国机械工程,2018,29(15):1834-1839.
LIU Zhengyu, TANG Wei, WANG Xuesong, et al. Battery State Estimation of Battery Pack Based on Dual Time Scale Extended Kalman Particle Filter Algorithm[J]. China Mechanical Engineering,2018,29(15):1834-1839.
[6] 刘伟龙,王丽芳,廖承林,等.基于模型融合与自适应无迹卡尔曼滤波算法的锂电池SOC估计[J].汽车工程,2017,39(9):997-1003.
LIU Weilong, WANG Lifang, LIAO Chenglin,et al. Estimation of Li-ion Battery SOC Based on Model Fusion and Adaptive Unscented Kalman Filtering Algorithm[J].Chinese Journal of Automotive Engineering ,2017,39(9): 997-1003.
[7] XIA B Z, SUN Z, ZHANG R F,et al. A Comparative Study of Three Improved Algorithms Based on Particle Filter Algorithms in SOC Estimation of Lithium Ion Batteries[J]. Energies, 2017,10(8): 1149-1163.
[8] 贠海涛,赵玉兰,钟再敏.基于龙贝格状态观测器的车载辅助动力蓄电池SOC估计[J].中国机械工程,2010,21(20):2505-2509.
YUAN Haitao, ZHAO Yulan, ZHONG Zaimin. SOC Estimation of Vehicle Auxiliary Power Battery Based on Longberg State Observer[J].China Mechanical Engineering, 2010,21(20):2505-2509.
[9] SITTERLYM, WANG L Y, YIN G G, et al. Enhanced Identification of Battery Models for Real-time Battery Management[J]. IEEE Transactions on Sustainable Energy, 2011, 2(3):300-308.
[10] 王笑天,杨志家,王英男,等.双卡尔曼滤波算法在锂电池SOC估算中的应用[J]. 仪器仪表学报,2013,34(8):1732-1738.
WANG Xiaotian, YANG Zhijia, WANG Yingnan, et al. Application of Dual Extended Kalman Filtering Algorithm in the State-of-charge Estimation of Lithium-ion Battery[J]. Chinese Journal of Scientific Instrument, 2013,34(8):1732-1738.
[11] 赵天意,彭喜元,彭宇,等.改进卡尔曼滤波的融合型锂离子电池SOC估计方法[J].仪器仪表学报,2016,37(7):1441-1448.
ZHAO Tianyi, PENG Xiyuan, PENG Yu, et al. Lithium-ion Battery SOC Estimation Method with Fusion Improved Kalman Filter[J]. Chinese Journal of Scientific Instrument, 2016,37(7):1441-1448.
[12] DIVERSI R, GUIDORZI R. The Frisch Scheme in Multivariable Errors-in-variables Identification[J]. European Journal of Control, 2017,37: 43-53.
[13] DIVERSI R, GUIDORZI R. A Covariance-matching Criterion in the Frisch Scheme Identification of MIMO EIV Models[J]. IFAC Proceedings Volumes, 2012,45(16):1647-1652.
