0 引言
锻造液压机是一种典型的机电液一体化复杂系统,高频次的锻造工艺、瞬时变化的机械载荷、液压回路的卸载冲击等,极易导致压机系统的振动,降低锻件精度,甚至影响机组寿命[1]。国内外学者针对锻造液压机振动机理及控制进行了研究。安国平等[1]从锻压机械的受力和能量角度出发,指出不同的卸载斜率在卸载时有不同的后果。黄云峰等[2]认为压力突变时引起液压机振动的主要原因是工作缸中液体储存的较大能量的突然释放。高俊峰等[3]、陈柏金等[4]针对多台快锻液压机的应用实践,分析了液压瞬变与管道振动的影响。沈文奇等[5]推导了大型压机理想卸压曲线,并借助MATLAB/Simulink逆向仿真模型得到平稳卸压时的电压控制信号。张友亮等[6]基于AMESim建立了快锻压机液压系统中比例节流阀和泄压回路的仿真模型,分析了主缸泄压特性。CHEN等[7]基于AMESim和Simulink软件建立了300MN模锻压机液压系统联合仿真模型,并分析其动态特性。
上述研究从机械本体或者液压系统方面考虑了液压机的振动机理及控制策略,但液压机是一个复杂的机-电-液耦合系统,工作时系统处于高压状态,设备本体和液压系统均储存极大的弹性变形能[8],当系统卸载时,压机瞬间受到很大的冲击。考虑到卸荷冲击对锻造液压机本体结构和液压系统的耦合振动,本文提出了基于ADAMS和AMESim的联合仿真技术[9-10],考虑机械系统的弹性,建立液压机机-液联合弹性动力学模型,分析系统振动规律,并通过实验验证模型的准确性。
1 锻造液压机联合仿真模型
本文以YA32-315液压机为研究对象,其工作循环包括:主缸快速下降—慢速下降加压—保压—泄压—换向上升,主要液压元件参数见表1。
表1 液压系统主要参数
Tab.1 Main parameters of hydraulic system

液压泵流量(L/min)63电机转速(r/min)1000溢流阀压力(MPa)25三位四通阀流量(L/min)100充液阀流量(L/min)500充液阀开启压力(MPa)0.3液压缸活塞直径(mm)400液压缸杆径(mm)350
1.1 弹性动力学模型
随着现代机械系统朝着高速、重载、高精度方向发展,系统刚性运动与其自身变形耦合产生的弹性动力学问题已成为亟需解决的关键问题。锻造压机工作时,超大的载荷导致设备本体发生较大的弹性变形,考虑压机在偏载工况下的空间振动,必须建立本体系统的柔性振动模型[11]:
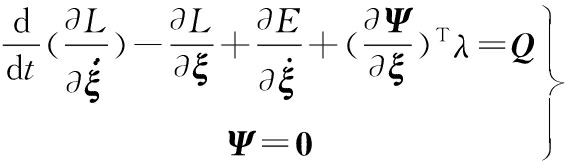
(1)
式中,ξ为广义坐标,由x、y、z,欧拉角ψ、θ、φ和模态坐标qi组成;L为拉格朗日函数,L=T-W, T和W分别为系统动能和势能;E为耗散能;Q为广义力;Ψ为约束方程;λ为拉氏乘子。
动能T可表示为[11]
(2)
其中,ρ为密度;v为速度;V为体积;mP为节点质量;IP为节点惯性张量;![]() 为参考点B相对于整体坐标系的角速度在局部坐标系的斜方阵表示。整理成广义质量阵和广义坐标的组合,表示为
为参考点B相对于整体坐标系的角速度在局部坐标系的斜方阵表示。整理成广义质量阵和广义坐标的组合,表示为
(3)
式中,M(ξ)为广义质量矩阵。
势能W可表示为[11]
(4)
式中,K(ξ)为广义刚度矩阵;Wg(ξ)为重力势能。
耗散能E可表示为[11]
(5)
式中,D为阻尼系数矩阵。
将式(3)~式(5)代入式(1)可得

(6)
1.2 联合仿真模型
考虑本体和液压系统的耦合作用以及机械系统的弹性,基于ADAMS、AMESim、ABAQUS,建立锻造液压机联合仿真模型,如图1所示。
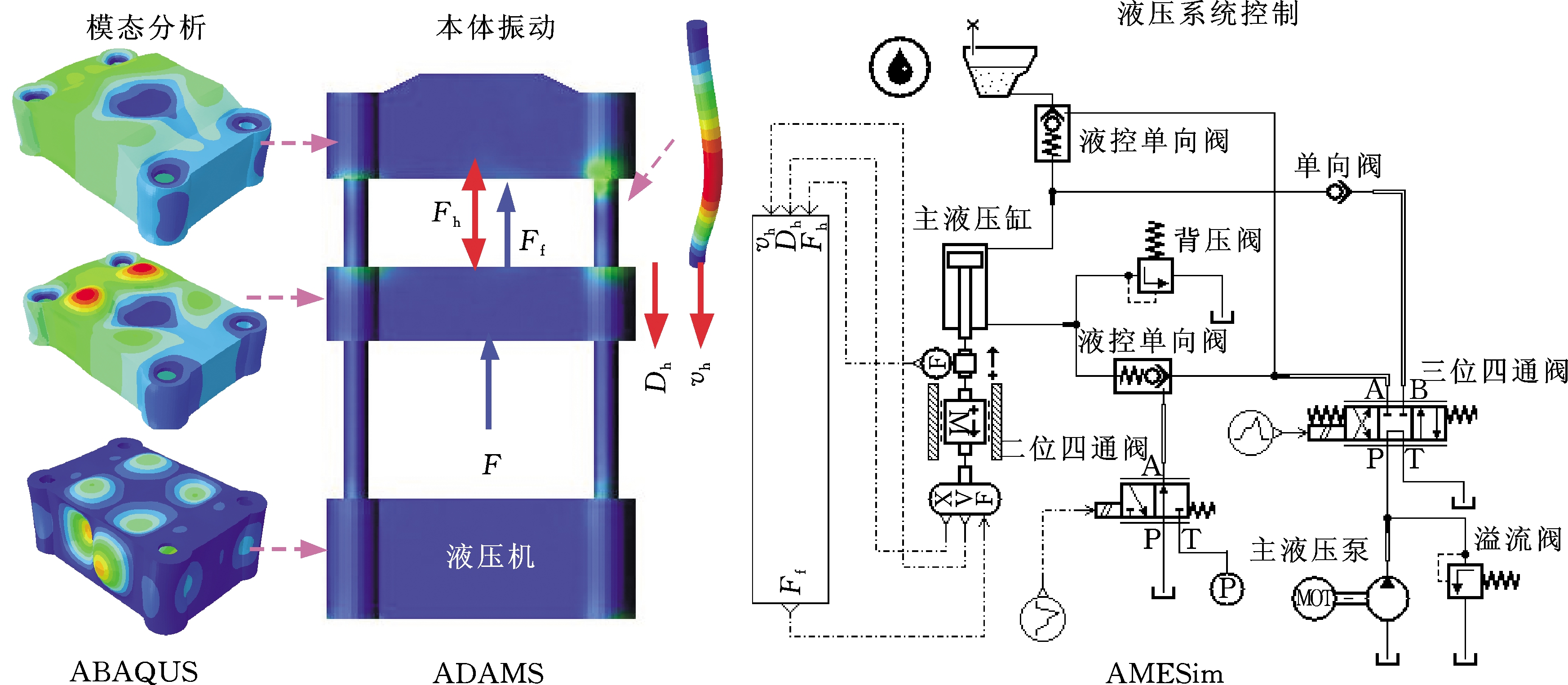
图1 联合仿真原理图
Fig.1 Schematic diagram of co-simulation
首先,基于ABAQUS软件完成压机本体的模态分析,然后将带有应力、变形信息的模态文件导入ADAMS中,建立锻造液压机弹性动力学模型,为简单起见,本文忽略拉杆预紧力的影响,将立柱实心化,顶部与上横梁通过节点固连。在AMESim软件中建立锻造液压机液压系统控制系统模型,并实现与ADAMS的无缝连接和数据共享。图1中,锻造力F为本体系统负载,选择动梁液压缸位置受力Ff作为ADAMS输出,即AMESim输入,其大小等于锻造力减去动梁与立柱的摩擦力。摩擦类型为库仑摩擦,静摩擦因数为0.1,动摩擦因数为0.05。通过AMESim模型计算出液压缸作用力Fh、活塞位移Dh、活塞速度vh作为ADAMS中锻造液压机相应力、位移及速度的输入。
联合仿真后,锻造力及液压缸推力曲线、活塞行程曲线和液压缸压力曲线见图2~图4。可以看出,0~3 s为快速下压段,4~6 s为加载段,慢速下压,6~9 s为保压段,9 s开始卸载,9~11 s为回程段。卸载时,由于压机本体和液压系统均储存有很大的弹性势能,卸荷时突然释放,产生很大的液压冲击并引起振动。在3 150 kN中心载荷作用力及表1所示参数下,其振动持续时间约0.03 s,活塞行程波动为3.3 mm(最大值和最小值的差值,后同),不同锻造力和系统压力对冲击特性会有一定影响,其影响规律见后文。

图2 锻造力及液压缸推力曲线
Fig.2 Forging force and hydraulic cylinder thrust curve

图3 活塞行程曲线
Fig.3 Piston stroke curve
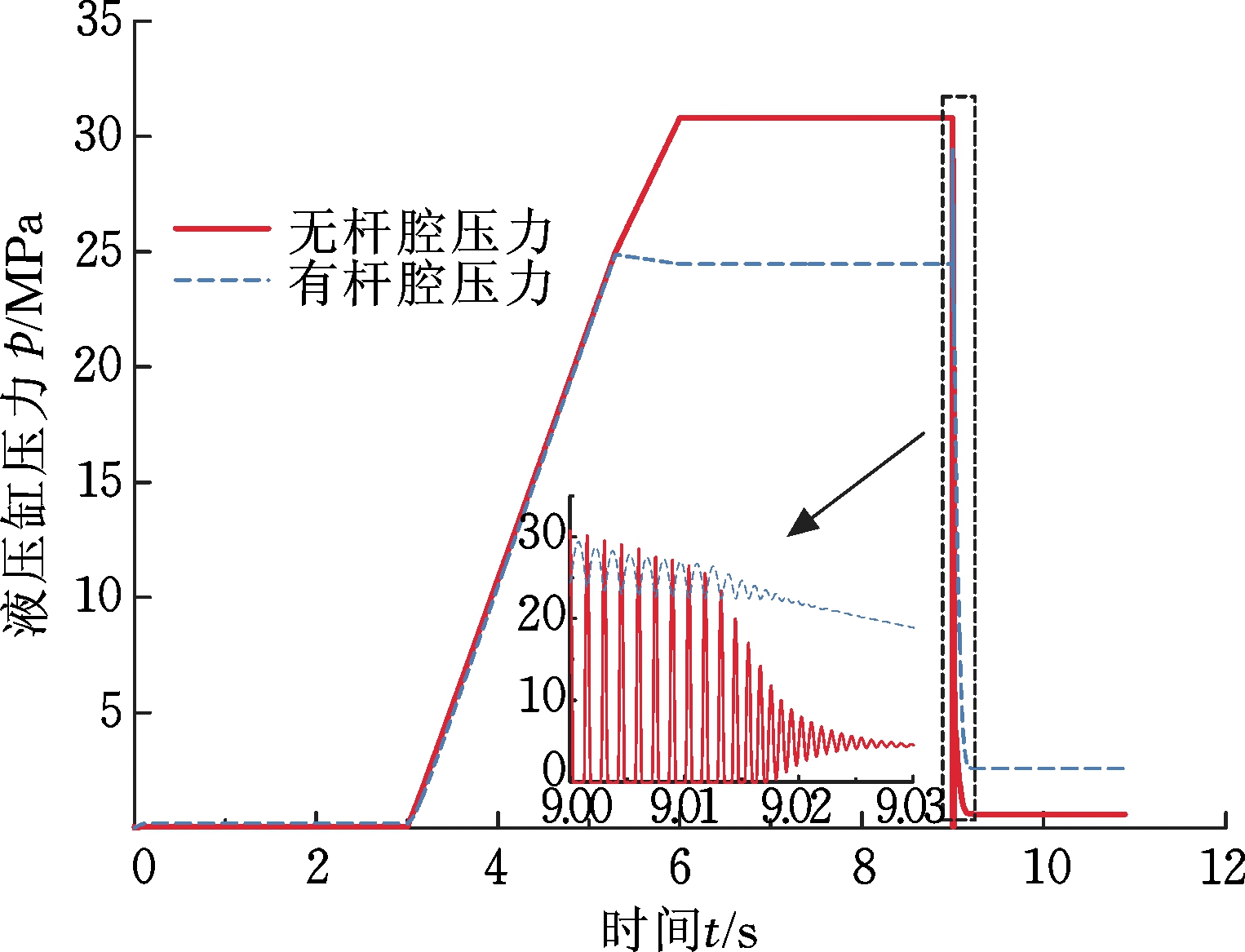
图4 液压缸压力变化曲线
Fig.4 Hydraulic cylinder pressure curve
液压机保压阶段的等效应力和等效应变云图见图5,最大位置均位于梁与拉杆接触位置,最大等效应力为169 MPa,最大等效应变为1.2×10-3。

图5 压机等效应力和应变分布云图
Fig.5 Equivalent stress and strain distribution of press
2 不同参数下液压冲击特性
2.1 不同锻造力
为研究不同锻造力对液压冲击的影响,选取锻造力如图6所示,最大锻造力分别为1 MN、2 MN、3 MN和4 MN。和前文相同,3~6 s为加载阶段,6~9 s为保压阶段。

图6 不同锻造力曲线
Fig.6 Forging force curves
不同锻造力作用下,液压缸行程、活塞速度和液压缸推力变化如图7~图9所示。可以看出,随着锻造力的增大,活塞行程变小,锻造力为1 MN时行程为0.898 m,锻造力为4 MN时行程仅0.795 m。卸荷时,随着锻造力的增大,其位移、速度波动均增大。锻造力为1 MN时,位移波动为2.8 mm(最大值和最小值的差值,后同),速度波动为5.69 m/s;锻造力为4 MN时,位移和速度波动值分别为5.6 mm和21.35 m/s。而且随着锻造力的增大,其稳定时间变长,锻造力为1 MN时,稳定时间约15 ms;锻造力为4 MN时,稳定时间约30 ms。

图7 不同锻造力下液压缸行程曲线
Fig.7 Hydraulic cylinder stroke curve under different forging forces

图8 不同锻造力下活塞速度曲线
Fig.8 Piston speed curve under different forging forces
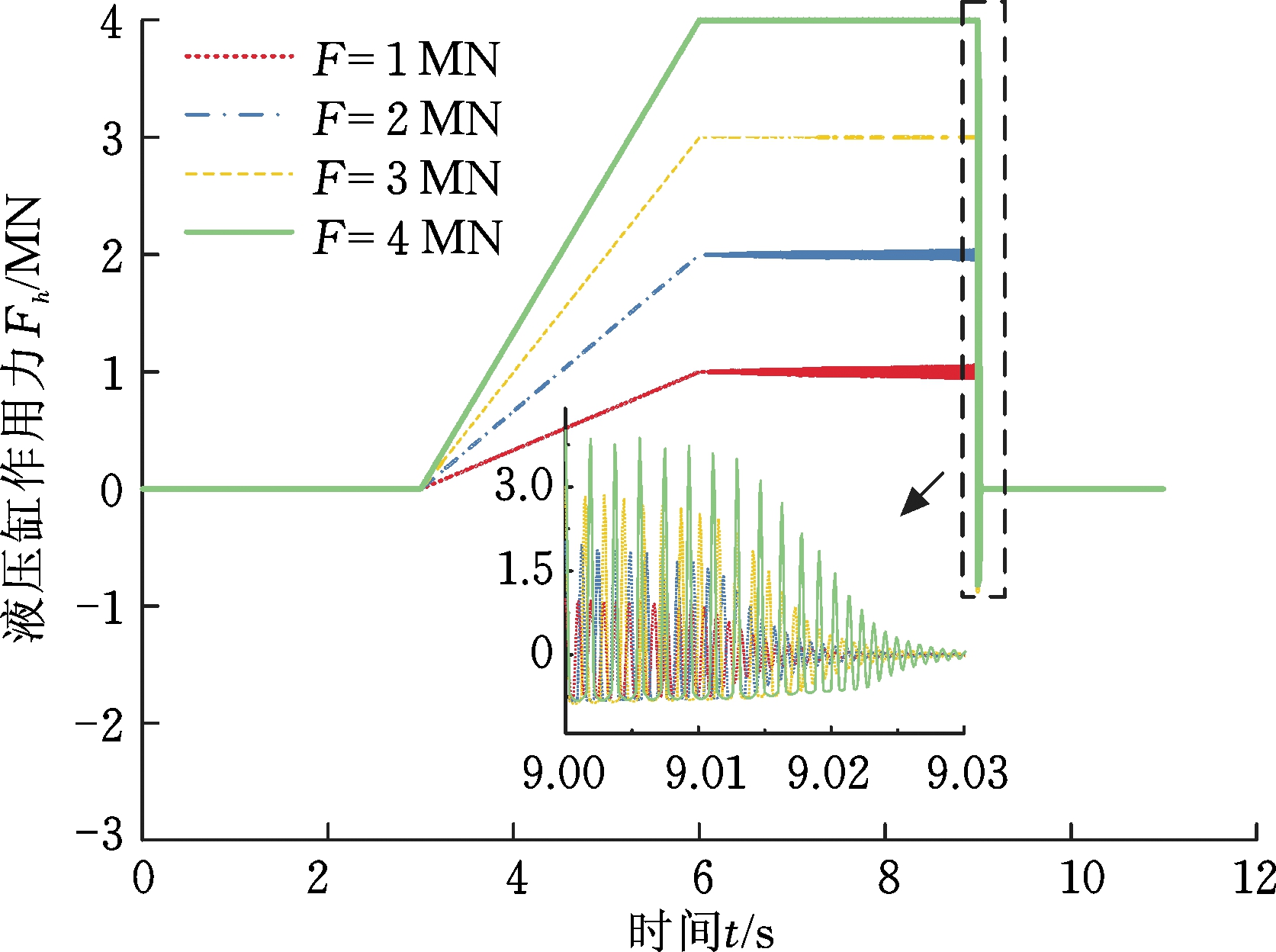
图9 不同锻造力下液压缸推力曲线
Fig.9 Hydraulic cylinder thrust curve under different forging forces
2.2 不同系统压力
为研究不同系统压力对液压冲击的影响,设置溢流阀压力分别为10 MPa,15 MPa,20 MPa,25 MPa和30 MPa。载荷加载方式与前文相同,最大值设为2 MN。
不同系统压力作用下,液压缸行程、活塞速度和液压缸推力变化如图10~图12所示。可以看出,随着系统压力的增大,活塞行程变大,系统压力为10 MPa时行程为75 mm,系统压力为30 MPa时行程为89 mm。卸荷时,不同压力下位移、速度波动值基本相同,位移波动为2.5 mm,速度波动为11 m/s,稳定时间约0.02 s。
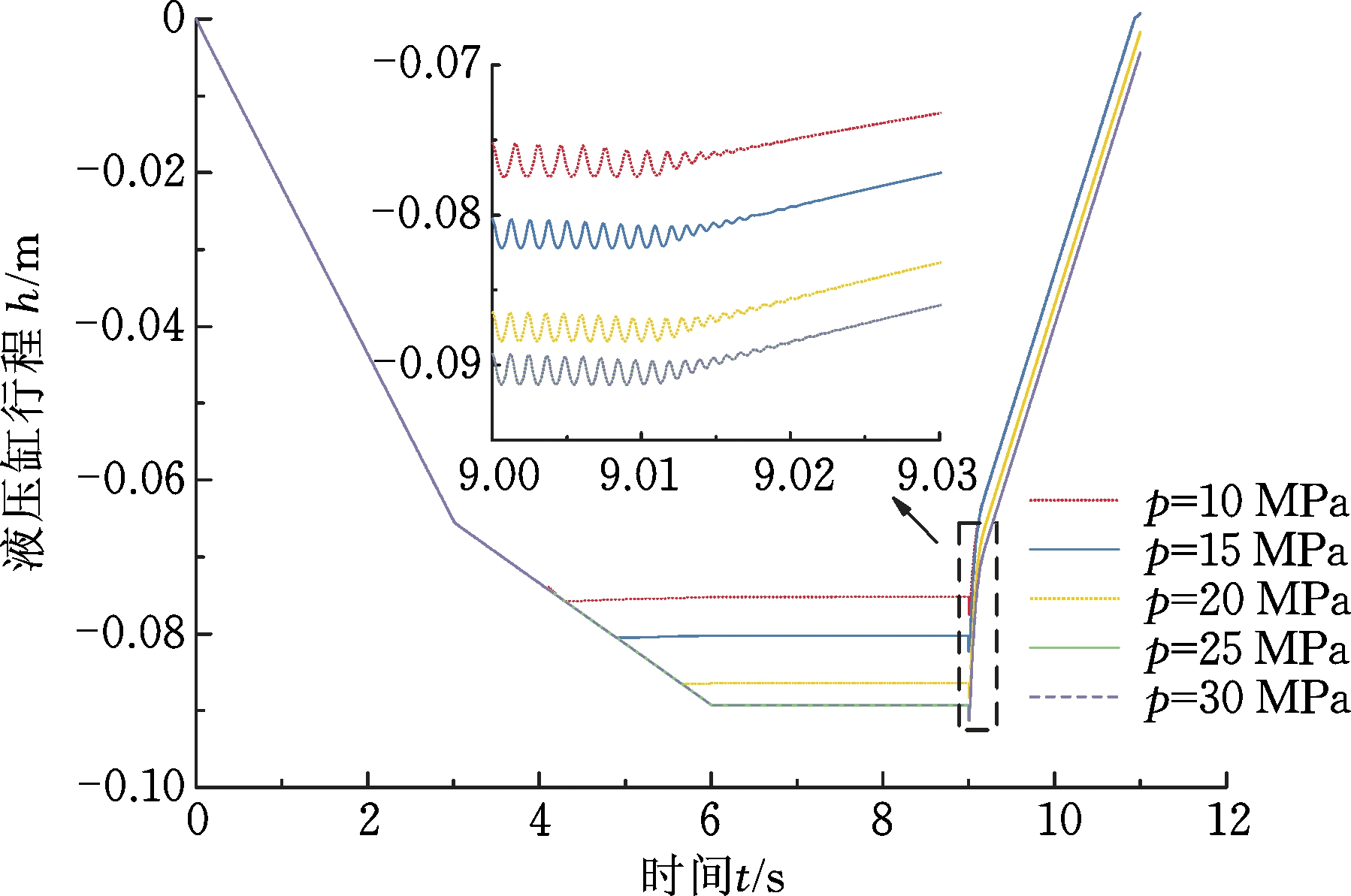
图10 不同系统压力下液压缸行程曲线
Fig.10 Hydraulic cylinder stroke curve under different system pressures
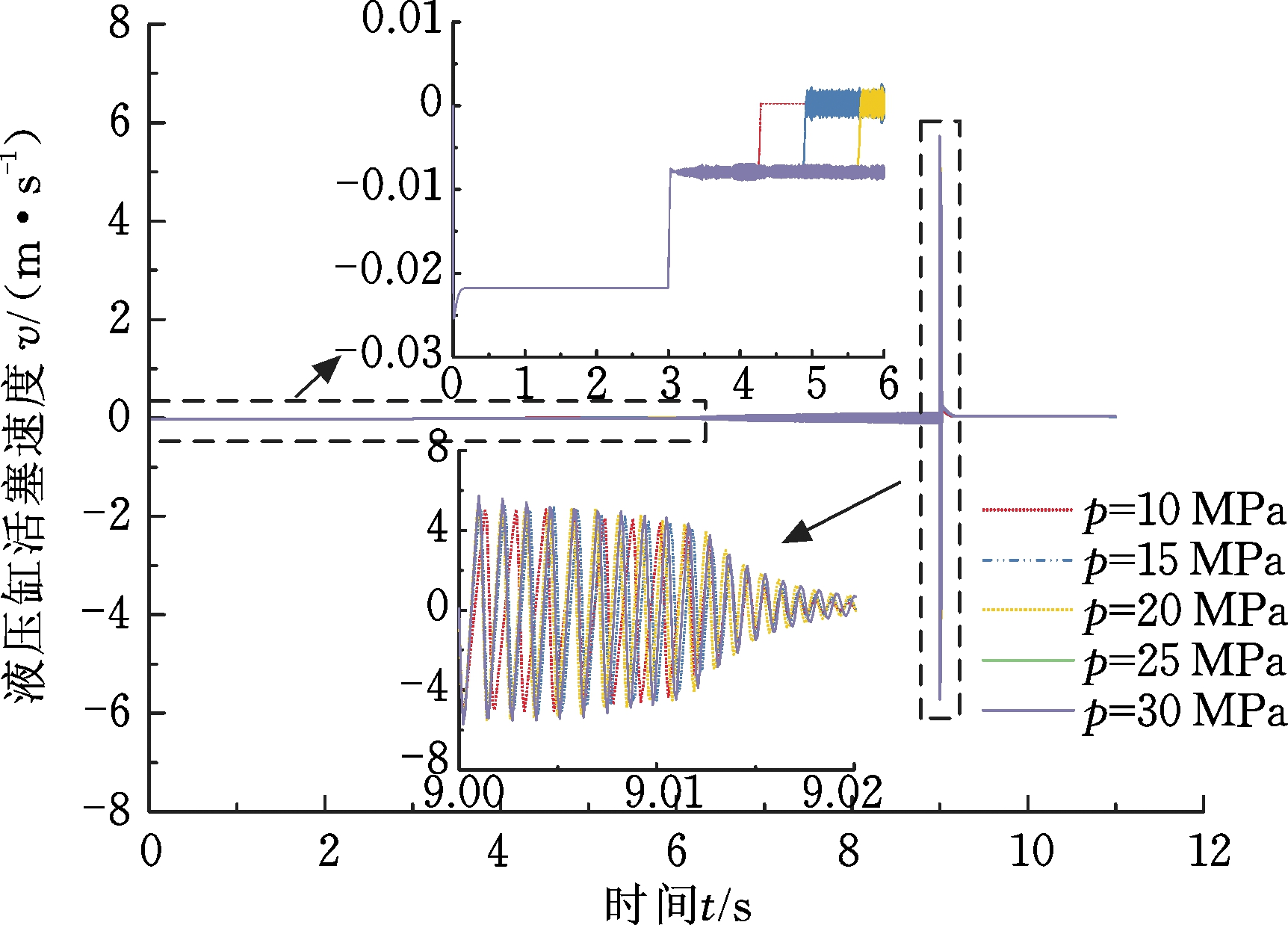
图11 不同系统压力下活塞速度曲线
Fig.11 Piston speed curve under different system pressures
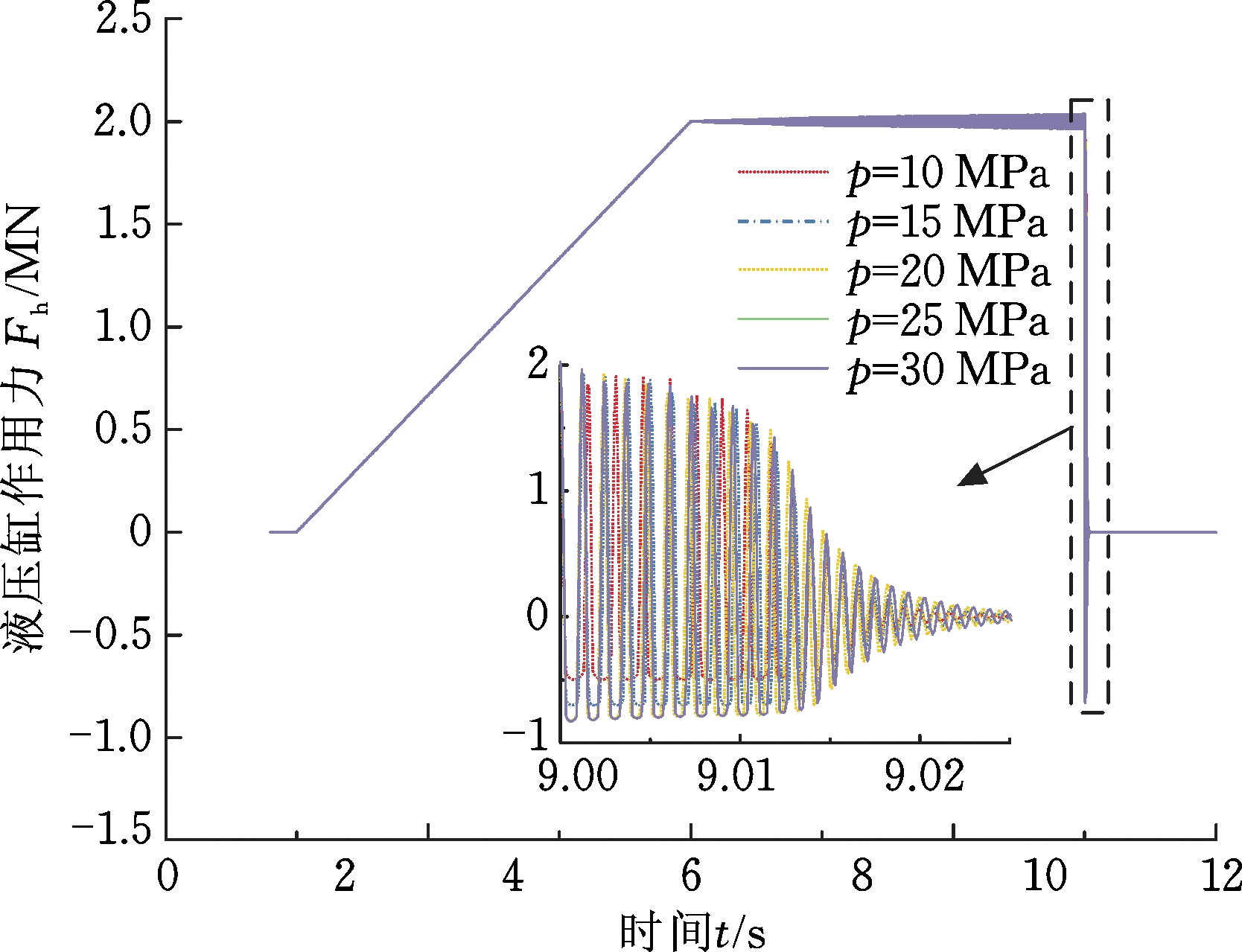
图12 不同系统压力下液压缸推力曲线
Fig.12 Hydraulic cylinder thrust curve under different system pressures
3 偏载振动特性
由于锻件结构的不均匀性,或者锻造位置对中性不佳,压机常处于偏载状态,故研究压机在偏载状态下的振动状态具有很好的现实意义。本文分别从X和Y方向对锻造液压机进行偏载振动特性研究,考虑设备能力,偏载量A取10 mm、20 mm、30 mm,偏载量B取10 mm、20 mm。载荷加载方式与前述相同,最大值设为额定载荷3 150 kN。图13为锻造液压机偏载示意图,O点为动梁中心,A和B分别为X向和Y向的偏载位移,Z向为动梁运动方向。
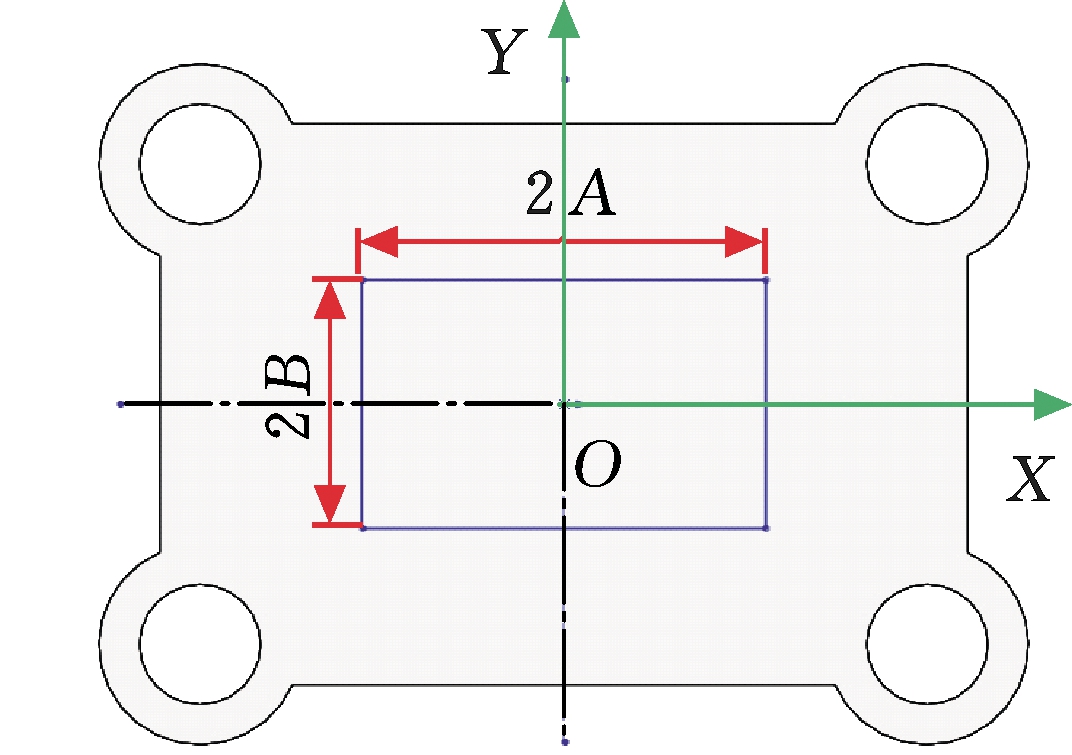
图13 锻造液压机偏载示意图
Fig.13 Schematic diagram on eccentric load of press
3.1 X向偏载
压机工作时,由于下梁固定,故卸荷冲击时,上梁的振动最为严重。X向偏载作用时,上梁X向位移、速度和加速度变化如图14所示。可以看出,由于载荷向X向偏移,动梁绕Y向偏转,导致上梁向-X向偏移,并在卸荷时产生冲击振动。中心载荷作用时,压机在X方向基本没有振动,随着偏载量的增大,上梁位移、速度和加速度相应增大。偏载量为30 mm时,其位移为-1.56 mm,位移、速度和加速度波动值分别为2.82 mm、0.44 m/s、298 m/s2。
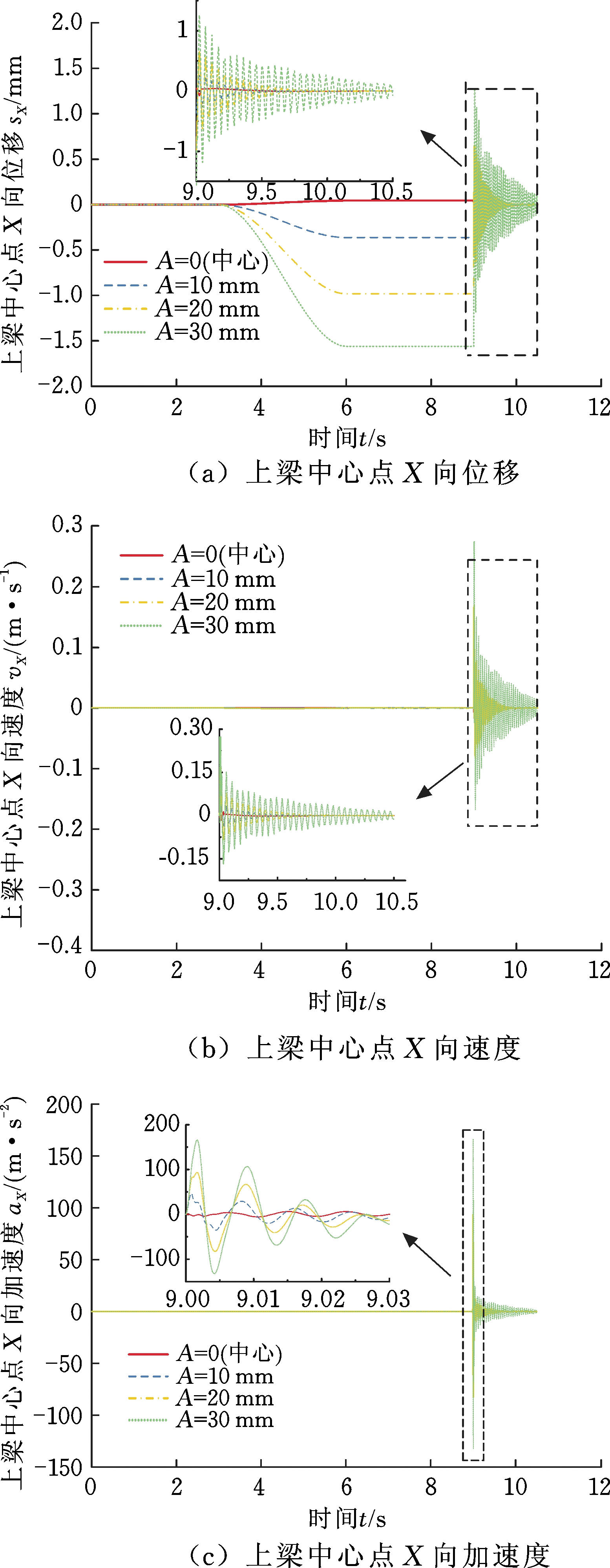
图14 X向偏载作用时上梁X向振动特性
Fig.14 X-direction vibration characteristics of upper beam when X-direction is biased
X向偏载作用时,上梁Z向(动梁运动方向)位移、速度和加速度如图15所示。可以看出,不同偏载量作用时,上梁Z向振动特性基本相同。由于Z向受工作载荷作用,上梁往Z向产生变形,当系统卸载时,也产生相应的振动,Z向最大位移、速度和加速度分别为0.97 mm、0.65 m/s、450 m/s2。与X向相比,其加速度值大,稳定时间短。
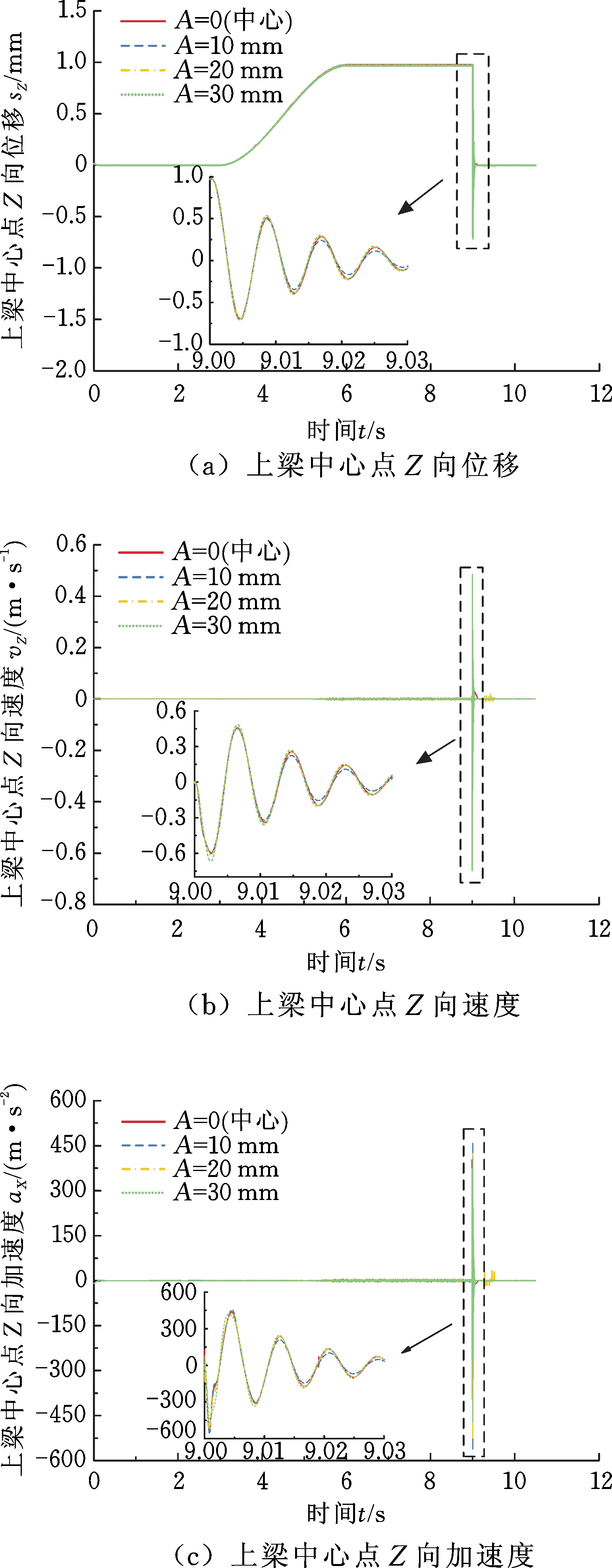
图15 X向偏载作用时上梁Z向振动特性
Fig.15 Z-direction vibration characteristics of upper beam when X-direction is biased
X向偏载作用时,压机保压阶段的等效应力分布如图16所示,可以看出,随着偏载量的增大,等效应力也随之增大。中心载荷时等效应力为139 MPa,30 mm偏载量时等效应力为237 MPa。
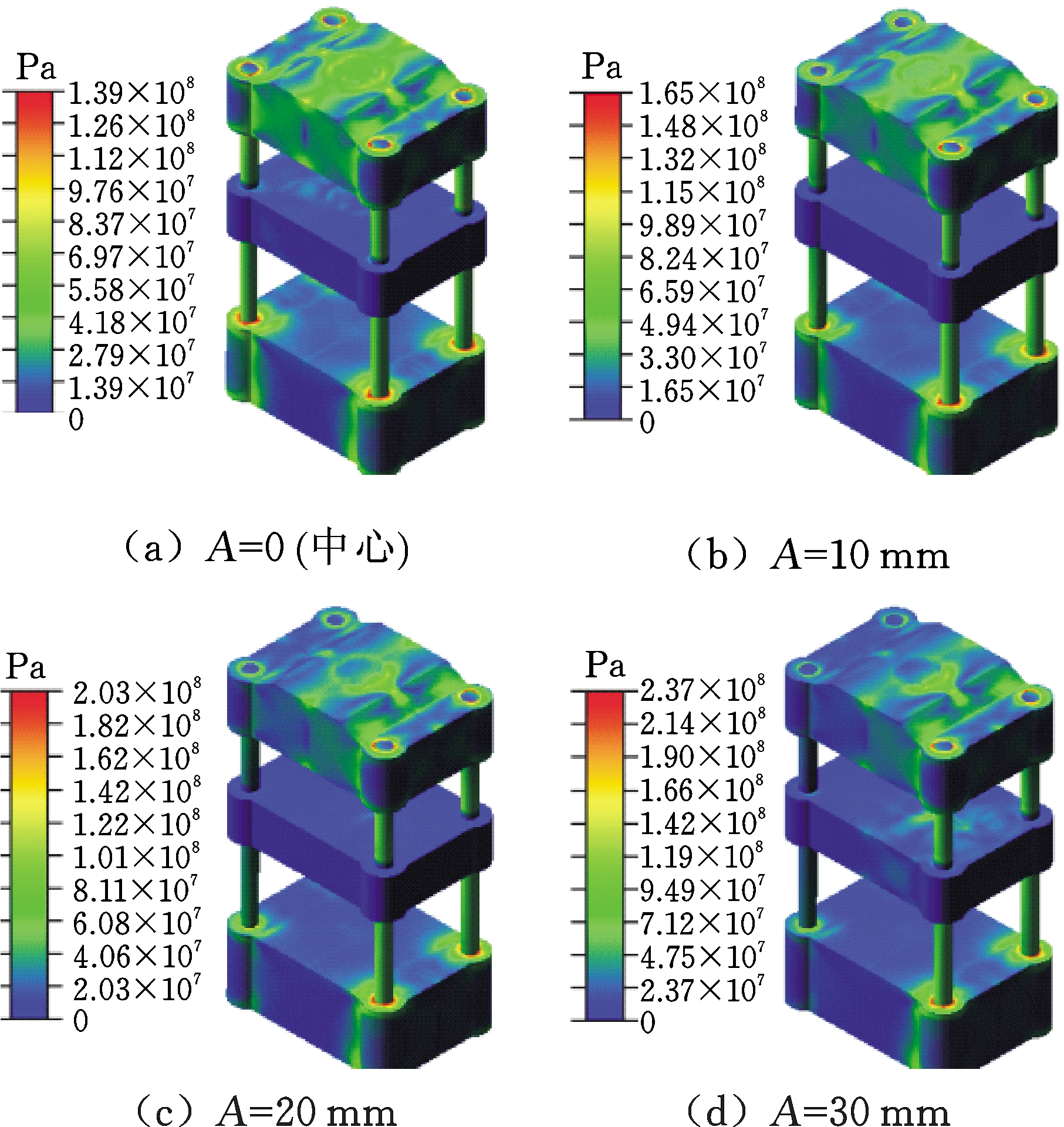
图16 X向偏载作用时压机等效应力分布
Fig.16 Equivalent stress and strain distribution when X-direction is biased
3.2 Y向偏载
Y向偏载作用时,上梁Y向位移、速度和加速度变化如图17所示。可以看出,由于载荷向+Y向偏移,动梁绕X向偏转,导致上梁向-Y向偏移,在卸荷时产生冲击振动。与X向偏载相同,随着偏载量的增大,上梁Y向位移、速度和加速度相应增大。偏载量为20 mm时,其位移为-1.88 mm,位移、速度和加速度波动值分别为3.45 mm、0.53 m/s、218 m/s2,对比X向偏载20 mm时,其振动幅值变大,这是由于压机X向尺寸大于Y向尺寸(YA32-315压机X向立柱间距为1 400 mm,Y向立柱间距为900 mm),X向抗弯刚度较大。
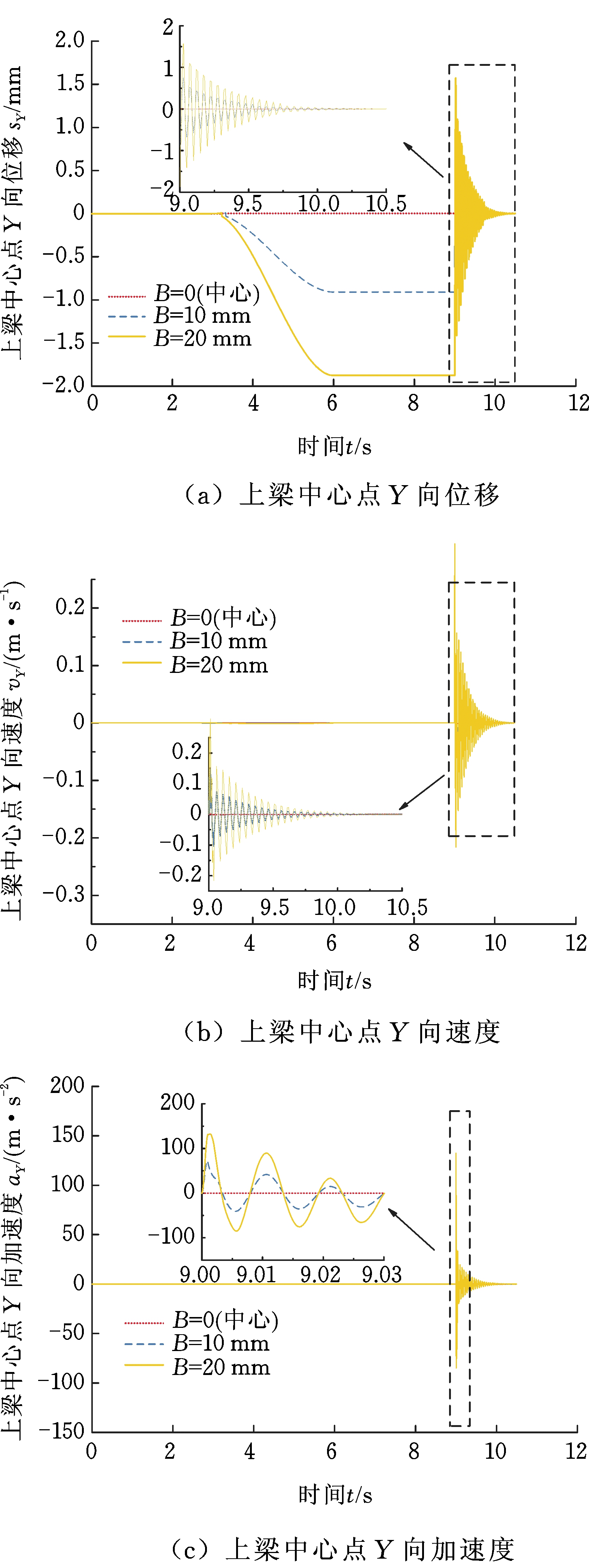
图17 Y向偏载作用时上梁Y向振动特性
Fig.17 Y-direction vibration characteristics of upper beam when Y-direction is biased
Y向偏载作用时,上梁Z向位移、速度和加速度如图18所示。可以看出,不同偏载量作用下,上梁Z向振动特性基本相同。这与X向偏载规律类似,不再赘述。
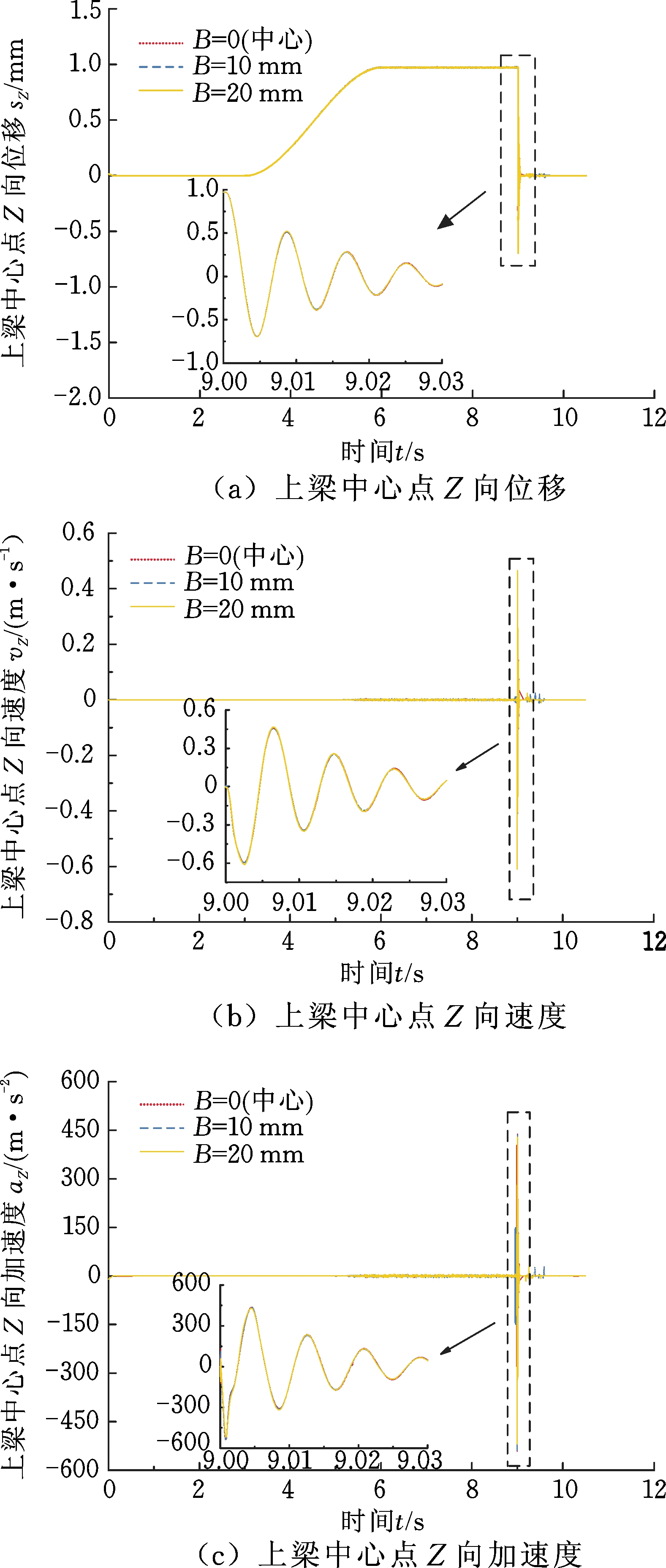
图18 Y向偏载作用时上梁Z向振动特性
Fig.18 Z-direction vibration characteristics of upper beam when Y-direction is biased
Y向偏载作用时,压机保压段的等效应力分布云图见图19,对比图16可以看出,与X向偏载相同,随着偏载量的增大,等效应力也随之增大。但由于Y向抗弯刚度低,故同等偏载量时,其等效应力值变大。中心载荷时等效应力为139 MPa,20 mm偏载量时等效应力为246 MPa。

图19 Y向偏载作用时压机等效应力分布
Fig.19 Equivalent stress and strain distribution when Y-direction is biased
4 振动测试及模型验证
为了验证仿真结果的准确性,对3 150 kN实验压机进行振动测试。由于设备原因,系统压力设为15 MPa,载荷最大值设为2 MN,载荷分为中心载荷和偏心载荷两种,偏载量为10 mm,对上横梁卸载过程进行加速度测试。上横梁测点位置如图20所示,传感器型号为4536-B-001(Bruel &Kjaer),采集系统为PXIe-1032(National Instruments)。
根据前文给定的工作制度进行实验验证,实验结果表明,仅在压机卸荷阶段,上横梁有较大的加速度波动,在其余阶段,加速度基本为零,与前文仿真结果一致,而振动持续时间基本在0.04 s以内。为了对比更加清晰,将卸载开始点9 s作为零初始时刻,将仿真与实验结果进行对比,如图21所示。可以看出Y向振动加速度大于X向振动加速度,与前述研究规律相同。X向最大加速度的仿真值为29.04 m/s2,实验值为31.61 m/s2,误差为8.13%;Y向最大加速度的仿真值为42.08 m/s2,实验值为46.22 m/s2,误差为8.94%;Z向最大加速度的仿真值为135.87 m/s2,实验值为144.48 m/s2,误差为5.96%。由于在建模过程中,立柱实心化导致刚度变大,故仿真结果稍小于实验结果。

图20 上横梁测点位置
Fig.20 Upper beam measuring point

图21 仿真实验对比情况
Fig.21 Comparison of simulation and experiment
5 结论
(1)以YA32-315锻造液压机为研究对象,考虑机械设备弹性,基于ADAMS、AMESim、ABAQUS联合仿真技术,建立了锻造液压机弹性动力学模型,分析了液压机在不同锻造力、不同系统压力下的液压冲击特性,锻造力越大,冲击越大,系统压力对冲击影响不大。
(2)研究偏载作用下的液压机本体振动规律,随着偏载量增大,压机振动变大,由于X向抗弯刚度大于Y向抗弯刚度,故相同偏载量时,Y向振动大于X向振动。
(3)完成了实验压机的振动测试,实验结果和仿真模型吻合良好,验证了模型的可行性和正确性。
[1] 安国平,阮中燕,毕新宇.锻压机械卸载时的力学行为[J].锻压机械, 1997(2):10-14.
AN Guoping, RUAN Zhongyan, BI Xinyu. Mechanical Analysis for Unloading of Metal Forming Machine [J]. Metalforming Machinery, 1997(2):10-14.
[2] 黄云峰,张剑慈,季英瑜.液压机在压力突变过程中平稳性的研究[J].机械制造,2012,50(6):89-90.
HUANG Yunfeng, ZHANG Jianci, JI Yingyu. Research on the Stability of Hydraulic Press in the Process of Pressure Mutation[J].Machinery, 2012,50(6):89-90.
[3] 高俊峰,孙茂,芦光荣,等.快速锻造液压机动载因数分析[J].锻压技术,2012,37(6):57-60.
GAO Junfeng, SUN Mao, LU Guangrong, et al. Dynamic Load Factor Analysis for High-speed Forging Hydraulic Press[J]. Forging & Stamping Technology, 2012,37 (6):57-60.
[4] 陈柏金,黄树槐,靳龙,等.16 MN快锻液压机控制系统研究[J].中国机械工程,2008,19(8):990-993.
CHEN Baijin, HUANG Shuhuai, JIN Long, et al. Development of the Control System for 16 MN Fast Forging Hydraulic Press [J]. China Mechanical Engineering,2008,19(8):990-993.
[5] 沈文奇.大型压机卸压冲击振动及其消减技术研究[D].长沙:中南大学,2013.
SHEN Wenqi. The Pressure Discharge Impact and Its Reduciton Technology Research of Large Press [D].Changsha:Central South University,2013.
[6] 张友亮, 田丽红, 杨喆, 等. 基于AMESim的快锻压机泄压特性仿真分析[J]. 锻压装备与制造技术, 2015, 50(6): 47-49.
ZHANG Youliang, TIAN Lihong, YANG Zhe, et al. Simulation Analysis of Pressure Relief Features for Quick Forging Hydraulic Press Based on AMESim[J]. Metalforming Equipment & Manufacturing Technology, 2015, 50(6): 47-49.
[7] CHEN Guoqiang, TAN Jianping. Study of Dynamic Characteristics for Hydraulic System on 300 MN Die-forging Press [C]//The 4th International Conference on Manufacturing and Industrial Technologies.Lisbon, 2017:1-6.
[8] MAKARYANTS G M, PROKOFIEV A B, SHAKHMATOV E V. Vibroacoustics Analysis of Punching Machine Hydraulic Piping[J].Procedia Engineering,2015,106:17-26.
[9] 董敏,马昌飞,杨利辉,等.基于AMESim与ADAMS联合建模的轧机厚控系统仿真[J].机床与液压,2017,45(5): 124-128.
DONG Min, MA Changfei, YANG Lihui, et al. Co-simulation of Strip Rolling Mill Gauge Control System Based on AMESim and ADAMS[J]. Machine Tool & Hydraulics,2017,45(5): 124-128.
[10] DU Heng, LIN Jianxin, ZHANG Yuan, et al. The Modeling and Simulation Analysis on Four Corners Leveling System in Composite Material Hydraulic Press Based on AMESim/ADAMS[J].Wseas Transactions on Systems and Control,2016,11:304-317.
[11] 陈立平,张云清, 任卫群,等.机械系统动力学分析及ADAMS应用教程[M].北京:清华大学出版社,2005:35-38.
CHEN Liping, ZHANG Yunqing, REN Weiqun, et al. Mechanical System Dynamics Analysis and ADAMS Application Course[M]. Beijing: Tsinghua University Press,2005:35-38.
