0 引言
气动肌肉(pneumatic muscle,PM)也称为气动肌肉执行器或流体肌肉,是一种管状的气动执行器,它由外面包裹一层高强度纤维编制层的密封橡胶软管组成。其中应用最为广泛的是MicKibben型气动肌肉[1]。作为一种拉伸驱动器,当其内部压强增大时,其膜片向圆周方向上延伸,并产生纵向的拉力和收缩;当其内部压强减小时,其膜片向圆周方向收缩,并纵向伸长[2]。气动肌肉具有柔顺性好、功率比大和成本低等优点,从而引起了国内外学者的广泛关注[3]。
然而,由于在气动肌肉运动过程中橡胶管的拉伸与变形、编织网之间以及编织网与橡胶管之间的摩擦[4]等因素的共同作用,会使其在运动过程中产生明显的位移/气压和力/位移迟滞现象[5]。迟滞不仅会降低系统的控制精度还会产生相位失真,进而降低系统的不稳定性,从而给气动肌肉精确的位置控制和力控制带来极大的挑战[6]。为了消除迟滞的影响,提高气动肌肉的控制精度,国内外学者进行了大量的研究,提出了诸多迟滞模型。
气动肌肉的迟滞可分为力/位移迟滞和位移/气压迟滞。目前,针对气动肌肉力/位移迟滞建模的研究较多。MINH等[7-8]采用Maxwell模型建立了气动肌肉的力/位移迟滞模型,并采用分段线性化的几何方法对Maxwell模型中的参数进行了辨识,最终将其成功应用到单根气动人工肌肉-质量系统的轨迹跟踪控制中,验证了所建立的气动人工肌肉迟滞模型的正确性。SCHREIBER等[9]采用Preisach模型对一种对称拮抗式布局的气动肌肉关节运动过程中所产生的力/位移迟滞进行了建模和前馈补偿控制研究,取得了较好的效果。
由于气动肌肉的力/位移迟滞模型实验设备较为复杂,而其位移/气压迟滞实验所需实验设备少,操作和测量简单,因此越来越多的学者开始尝试利用气动肌肉的位移/气压迟滞来解决其控制问题。KOSAKI等[10]采用Preisach模型来描述气动人工肌肉的迟滞现象,并借助学习矢量化网络方法来解决因外部负载变化导致的迟滞特性的变化。由于运动速度的变化也会使得气动人工肌肉的迟滞特性发生改变,因此KOSAKI等[11]在气动人工肌肉的轨迹跟踪控制中采用自适应参数辨识法对前述Preisach模型中的参数进行在线辨识,取得了良好的控制效果。ITO等[12]采用stop算子对气动肌肉的位移/气压迟滞现象进行建模,并将其应用于一种由气动肌肉驱动的并联平台的控制中。但在现有的文献中,尚未见到将Krasnosel’skii-Pokrovskii(KP)模型应用于气动肌肉的位移/气压迟滞建模研究中。
本文分别采用KP模型和多项式模型来描述气动肌肉中的位移/气压迟滞现象,通过搭建气动肌肉位移/气压迟滞实验台获取其迟滞实验数据,并与参数辨识所得到的拟合曲线相比较,对比两种模型参数辨识的结果。
1 模型分析
1.1 Krasnosel’skii-Pokrovskii模型
Krasnosel’skii-Pokrovskii模型(简称KP模型)是Preisach模型的改进,它的构造思想与Preisach模型的构造思想相似,与Preisach模型不同之处主要在于对迟滞算子的改进:Preisach算子γαβ[x(t)]的边沿为阶跃型函数,又称为继电器算子(图1),而KP算子则将Preisach模型中的非连续的迟滞算子改为连续的迟滞算子(图2),算子的上升和下降边沿是连续函数。
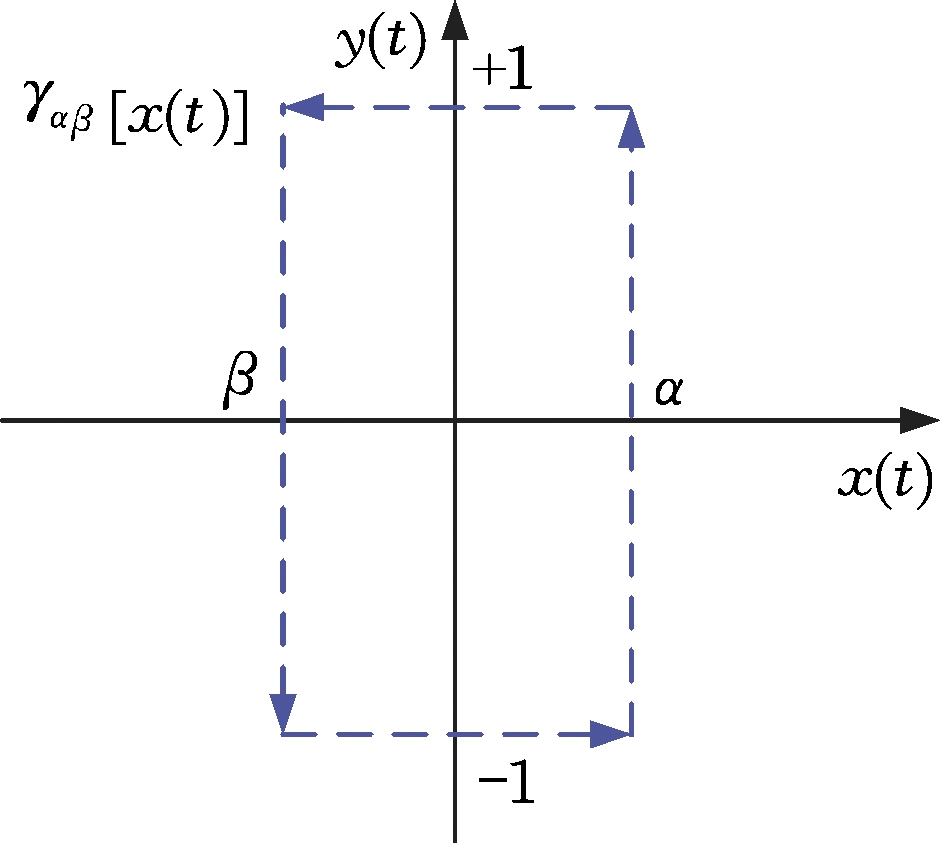
图1 Preisach算子
Fig.1 Preisach operator

图2 KP算子
Fig.2 KP operator
KP模型基本思想是认为迟滞现象是由一系列KP算子叠加而成的,其数学表达式为
(1)
式中,x(t)和y(t)分别为KP模型的输入与输出;H(·)为KP函数;kp[x,ξp]为KP算子;μ(p)为Preisach平面的密度函数。
令P为Preisach平面的积分区域,该区域可表示为
P={P(p1,p2)∈R2|α≤p1≤p2≤β}
(2)
其中,α、β分别为系统输入的最小值与最大值。
上述KP算子的数学表达式为
(3)
式(3)中,记忆变量ξp(t)的值依赖于KP算子kp,并且根据输入变化率![]() 方向的变化而更新,r(x(t))为其边界函数。记忆变量与边界函数表达式分别如下:
方向的变化而更新,r(x(t))为其边界函数。记忆变量与边界函数表达式分别如下:
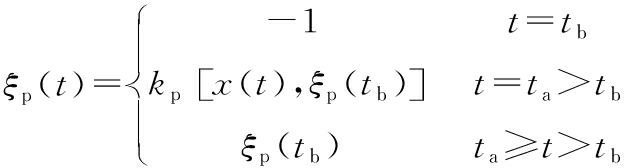
(4)
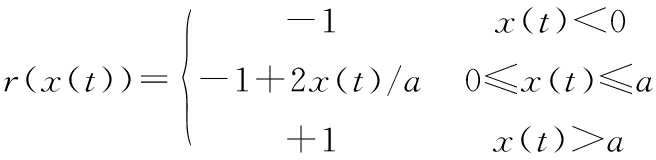
(5)
式中,t表示当前时刻;tb表示上一时刻;ta表示下一时刻。
为了便于计算,表达式的积分函数形式可以根据数学积分的意义转化为代数叠加求和的形式[13]。转化方法是对式(1)中的积分区域Preisach平面采用均匀分布的l条水平直线和垂直直线划分成网格,离散化的网格数共有N=(l+1)(l+2)/2个,每个网格的左下节点坐标为式(2)中的(p1, p2)。通过下式可计算出p1和p2:
(6)
Δx=(β-α)/(l+1)=a i≥j
i=1,2,…,l+1 j=1,2,…,i
式中,i、j分别为第i个和第j个网格线;Δx为网格宽度。
经过离散化之后,每个栅格对应的KP算子的平均密度为uij,则KP迟滞模型(式(1))可以写成以下离散形式:
(7)
其中,kij[x(t),ξp]为每个网格对应的迟滞算子;uij为每个网格对应的平均密度。迟滞系统的输出y(t)等于所有KP模型的算子kij[x(t),ξp]乘以对应平均密度uij所得积的叠加。由式(7)可以看出,栅格线的数目l越大,迟滞模型的输出u(t)越接近于系统的实际输出,也即模型的精确度越高。但l的增加会导致计算量以及运算时间的增加,所以,在实际的控制系统中,需要根据控制目标的要求灵活合理地选择参数l。
1.2 多项式模型
参考文献[14],采用2个多项式分别拟合气动肌肉位移/气压迟滞曲线的上升段和下降段,这里气动肌肉多项式模型可以写成如下的形式:
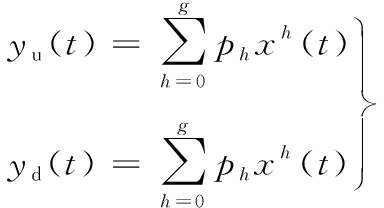
(8)
式中,yu表示迟滞曲线的上升段;yd表示迟滞曲线的下降段;x(t)为系统的输入;ph为多项式的系数;g为多项式的次数。
2 参数辨识
最小二乘法由于具有原理简单、收敛速度快和易于实现编程等特点,在系统参数辨识中得到了广泛应用。本节将采用递推最小二乘法(RLS)对KP模型中的待辨识参数进行辨识。
2.1 最小二乘法
最小二乘法的基本思想是通过使得真实值与估计值之间的误差平方和最小来寻找一组数据的最佳函数匹配。其目标函数由若干个误差函数φs(x)的平方和构成,一般可以写成
(9)
x=(x1,x2,…,xw)T
其中,x是实数集Rw中的点,且w≥o。将这类函数的问题极小化,可得
(10)
式(10)称为最小二乘问题。特别地,当每个φs(x)为关于x的线性函数时,称其为线性最小二乘问题。
相应的递推最小二乘算法的基本递推公式可以概括为[15]:
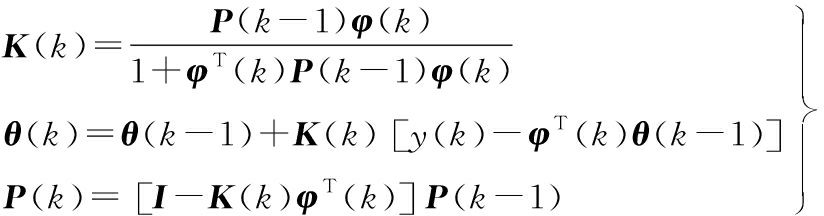
(11)
式中,P(k)为协方差矩阵;θ(k)为待辨识参数向量的估计值;K(k)为增益矩阵;φ(k)为观测矩阵。
在启动上述递推公式时需确定初值P(0)、θ(0)。这里采用文献[16]中介绍的方法,直接令
P(0)=γI θ(0)=ε
(12)
式中,γ为充分大的正实数(104~1010);ε为零向量或充分小的正的实向量;I为单位向量。
2.2 KP模型参数辨识
对于KP模型,当根据实际控制系统的精度确定了离散化参数l的数值之后,每个迟滞算子kij[x(t),ξp]也可以根据输入信号x(t)按照式(7)确定。
为了建立气动肌肉的位移/气压迟滞模型,需要根据实验得到的数据对KP模型的每个密度参数uij进行辨识[17]:
(13)
为了便于记忆和书写,将kij[x(t),ξp]简记为kij,并令
(14)
式(13)可以简写为
y(t)=φTθ
(15)
将式(15)代入式(11)即可完成KP模型的参数辨识。
对于多项式模型,由于在MATLAB中有成熟的函数可供调用,故本文采用MATLAB中polyfit函数进行多项式模型的参数辨识,该函数根据最小二乘法原理编写,其具体调用格式如下:
(16)
x=[x1, x2] y=[y1, y2]
式中,x为实验数据输入;y为实验数据输出;yu为上升段多项式拟合结果;yd为下降段多项式拟合结果;x1为上升段输入实验数据;y1为上升段输出实验数据;x2为下降段输入实验数据;y2为下降段输出实验数据;q为多项式的次数。
3 实验与结果分析
本节搭建气动肌肉的位移/气压迟滞特性实验平台,并通过实验得到其位移/气压迟滞的实验数据来实现两种模型的参数辨识及辨识效果的对比研究。
3.1 实验平台
气动肌肉的位移/气压迟滞实验装置如图3所示,它由气动肌肉、比例调压阀、空气压缩机、位移传感器、气压传感器和计算机组成。实验中所用到的主要元器件及其型号见表1。气动肌肉为德国费斯托公司所生产,一端固定于机架上,另一端可自由移动。位移传感器一端固定于机架上,另一端则与气动肌肉的自由端通过连接件相连,用于实时测量气动肌肉运动过程中的位移值。气压传感器与气动肌肉内腔相连,用于实时测量气动肌肉内腔的气压值。本文借助LabVIEW编写气动肌肉的控制和数据采集程序,控制程序生成的控制信号通过数据采集卡的模拟量输出接口(AO)控制比例阀的电压变化,进而控制气动肌肉内腔的气压变化,从而驱动气动肌肉的伸缩运动;数据采集程序用于采集气动肌肉运动过程中的位移和气压信号,实验中的气压和位移信号通过数据采集卡的模拟量输入接口(AI)输入数据采集卡中,再通过PCI总线与计算机通信输入计算机中进行数据的存储、数据处理和分析。系统的电气原理图见图4。

图3 气动肌肉迟滞特性实验
Fig.3 Hysteresis experiment of PM
表1 实验设备元件型号
Tab.1 Components of the experimental apparatus

元件型号主要参数厂商气动肌肉DMSP-20-500N长500 mm,内径20 mm费斯托位移传感器TEX-0150-415-002-205量程150 mmNovetechnik气压传感器SDE1-D10-G2-WQ4-L-PU-M8-G5最大测量气压1 MPa费斯托比例调压阀VPPM-6L-L-1-G18-0L10H气压调节范围0~1 MPa费斯托数据采集卡PCI-62308路模拟量输入,4路模拟量输出NI公司

图4 系统电气原理图
Fig.4 Electrical schematic diagram of the system
3.2 实验过程
实验过程如下:调节气动肌肉,使其初值状态下内部气压等于大气压。启动程序,调节比例调压阀使气动肌肉内部绝对气压缓慢地从0增至0.6 MPa,当其内部气压到达0.6 MPa后,再调节比例调压阀使其内部绝对气压缓慢降到0。通过LabVIEW编写的数据采集程序可得到气动肌肉充放气过程中的气压和位移数据。将气动肌肉的位移转换成收缩率,得到的位移/气压迟滞曲线如图5所示。
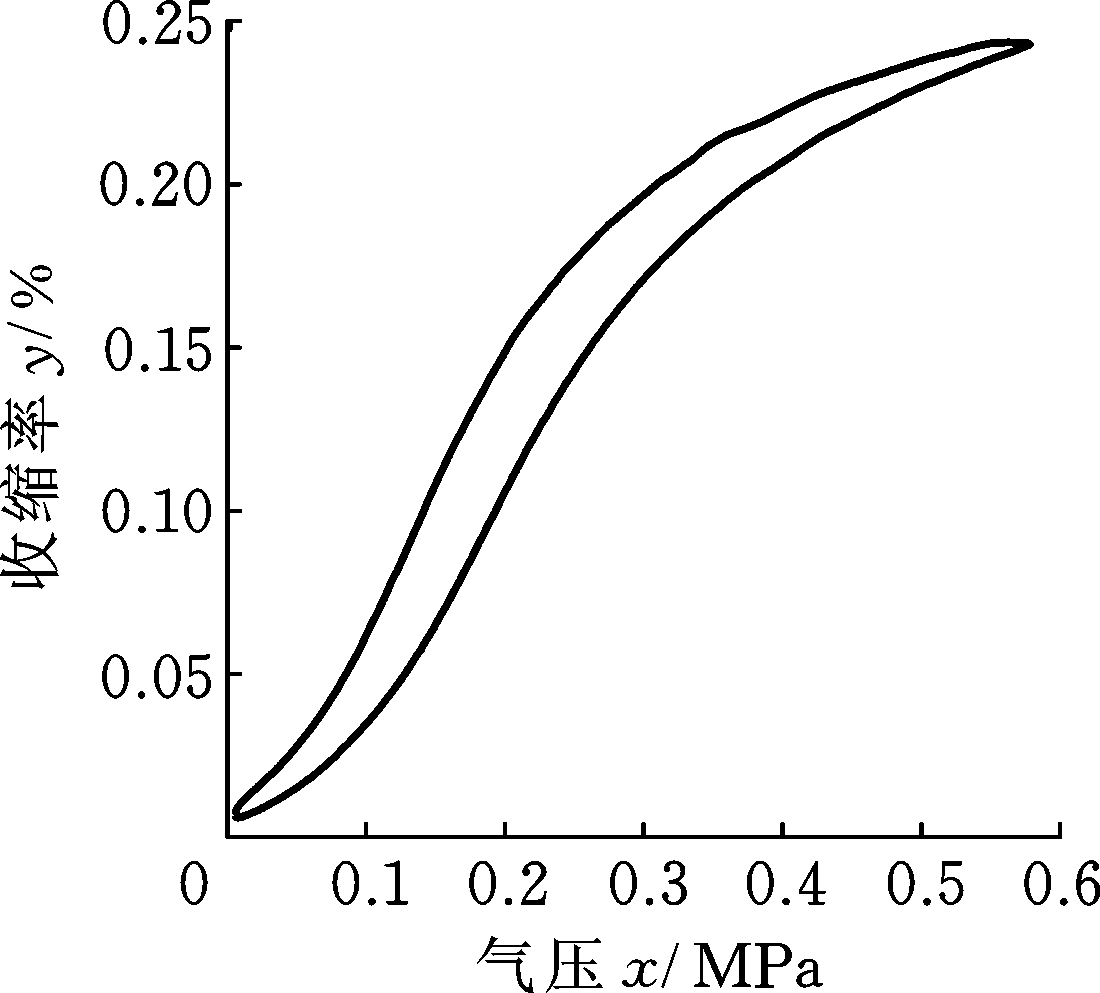
图5 气动肌肉位移/气压迟滞曲线
Fig.5 Displacement/Pressure hysteresis loop of PM
3.2 实验结果分析
在得到气动肌肉位移/气压迟滞曲线数据的基础上,采用第2节所述的递推最小二乘法分别对KP模型中的密度参数和多项式模型中的系数进行参数辨识。作为对比,KP模型的算子个数分别取200和300,多项式的次数分别取4和8,所得到的参数辨识结果分别如图6和图7所示,所得到的多项式系数如表2所示。从图6a中可以看出,KP模型基本上与实验数据吻合,但是呈现出一定程度上的波动,模型呈现出明显的“毛刺”现象,尤其在气动肌肉充气收缩到0.25 MPa气压左右时波动较大;图6b中KP模型几乎与实验数据完全重合,模型整体光滑,模型精度显著提高。
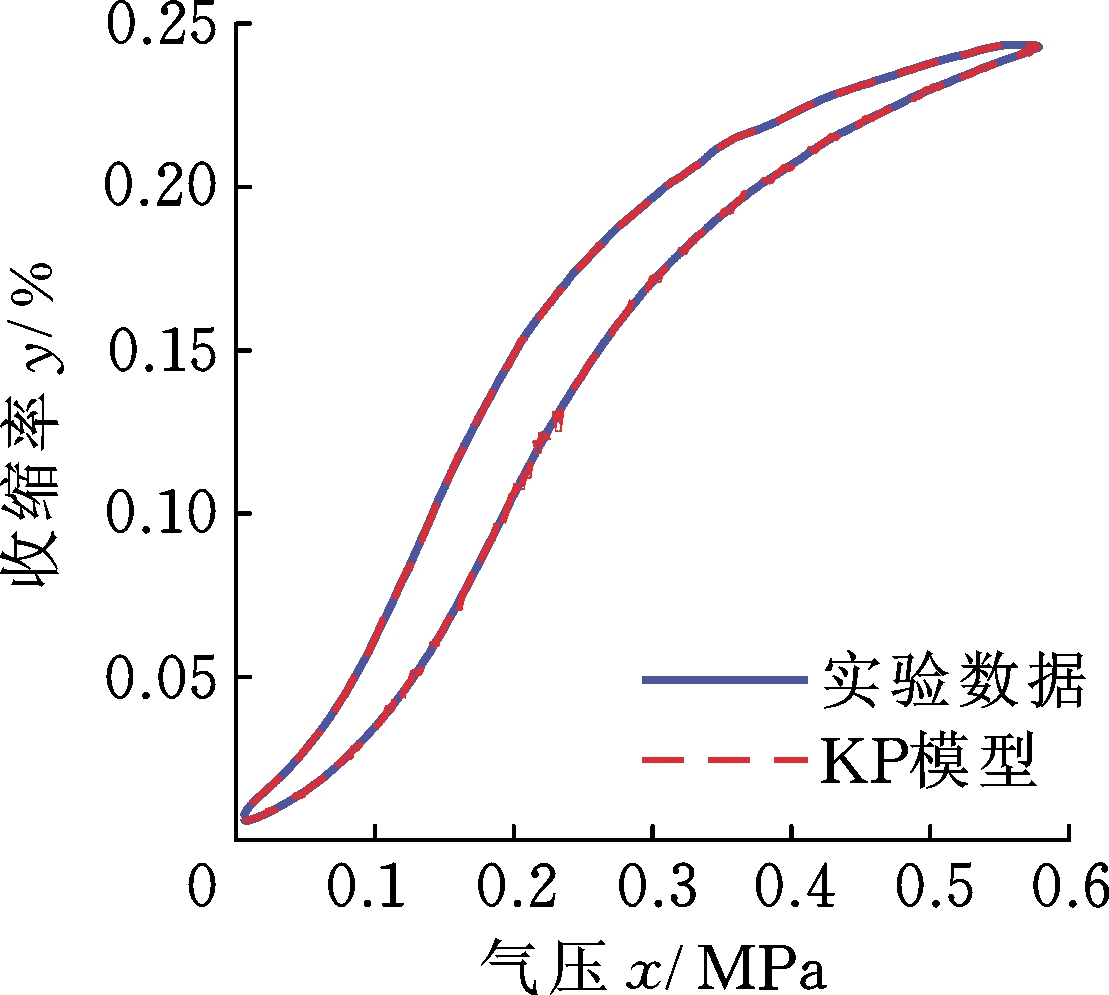
(a) 200个算子

(b) 300个算子
图6 KP模型辨识结果
Fig.6 Identification result of KP model
表2 多项式拟合系数
Tab.2 Polynomial fitting coefficient
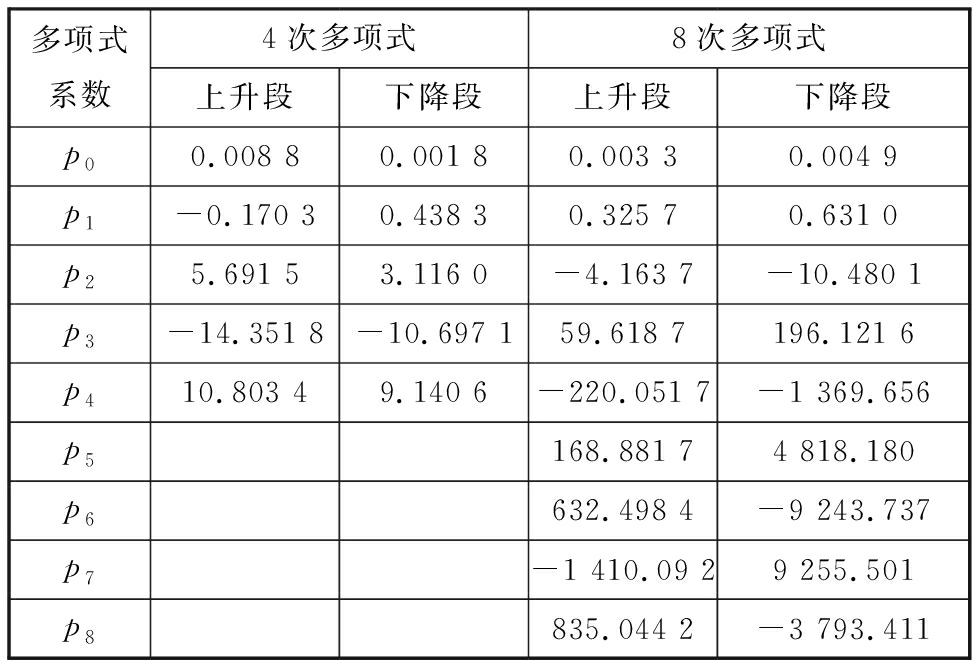
多项式系数4次多项式8次多项式上升段下降段上升段下降段p00.008 80.001 80.003 30.004 9p1-0.170 30.438 30.325 70.631 0p25.691 53.116 0-4.163 7-10.480 1p3-14.351 8-10.697 159.618 7196.121 6p410.803 49.140 6-220.051 7-1 369.656p5168.881 74 818.180p6632.498 4-9 243.737p7-1 410.09 29 255.501p8835.044 2-3 793.411
图7a所示为4次多项式的拟合结果,该模型无论是上升段还是下降段均与实验数据存在较大的建模误差,尤其在气压最大处误差最为显著。图7b所示为8次多项式的拟合结果,结果表明多项式模型的建模精度显著提高,多项式模型几乎与实验数据完全重合,可见提高多项式的次数能提高模型的精度。需要指出的是,虽然8次多项式能很好地拟合气动肌肉的位移/气压迟滞现象,但是与KP模型相比,多项式模型存在以下缺陷:①多项式模型需要针对模型的上升段和下降段分别建模,数据处理复杂,难以应用于后续的实时控制;②随着多项式次数的增加,多项式拟合可能会出现龙格现象,使得模型精度急剧变差;③逆模型难以求解,需要结合具体机构灵活应用,缺乏普适性[5]。
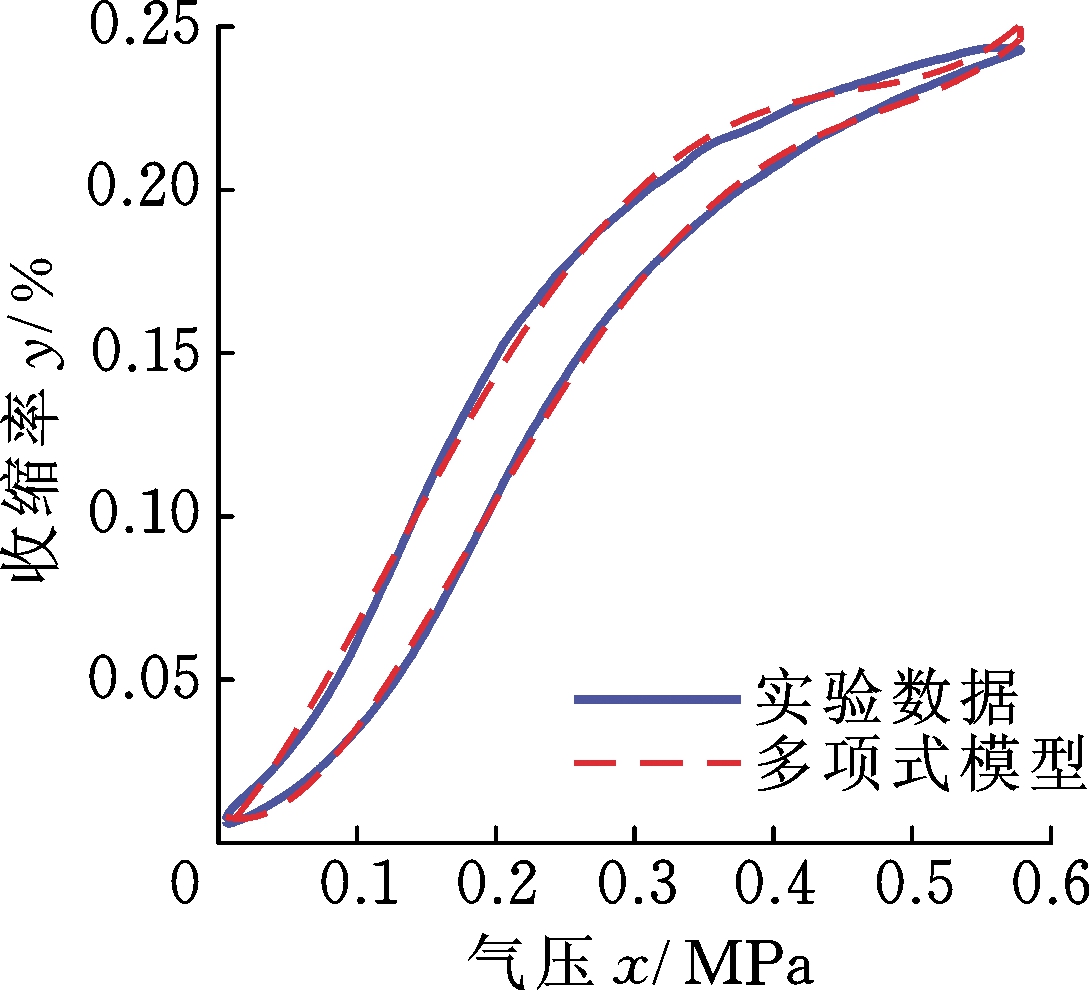
(a) 4次多项式

(b) 8次多项式
图7 多项式模型辨识结果
Fig.7 Identification result of polynomial model
为了更进一步量化比较两种模型的参数辨识效果,本文根据文献[18]所述公式计算理论模型输出yM与实际实验数据y之间的最大误差、均方差和平均误差:
emax=|max y-min yM|
(17)
(18)
(19)
所得的最大误差、平均误差和均方差以及两种模型在不同算子和次数下的计算时间如表3所示。从表3中可以看出,KP模型在算子个数由200增加到300时,上述3种建模误差显著减小,但计算时间也随之明显增加;多项式模型的精度随着多项式次数的增加而明显提高,其计算所需时间也随之增加。对比可以发现,随着算子个数的增加,KP模型的精度明显优于多项式模型,但是其计算所需的时间明显多于多项式模型,这是因为KP模型比多项式模型复杂,待辨识的参数也多于多项式模型。因此在实际应用中,KP模型的算子个数需要根据模型的精度和规模折中选取。虽然KP模型计算时间有所增加,但是多项式模型逆模型难以求解,需要结合具体机构灵活应用,缺乏普适性,而KP模型则可以直接应用于PID复合控制中。
表3 两种模型建模误差对比
Tab.3 Error comparison of KP and polynomial models
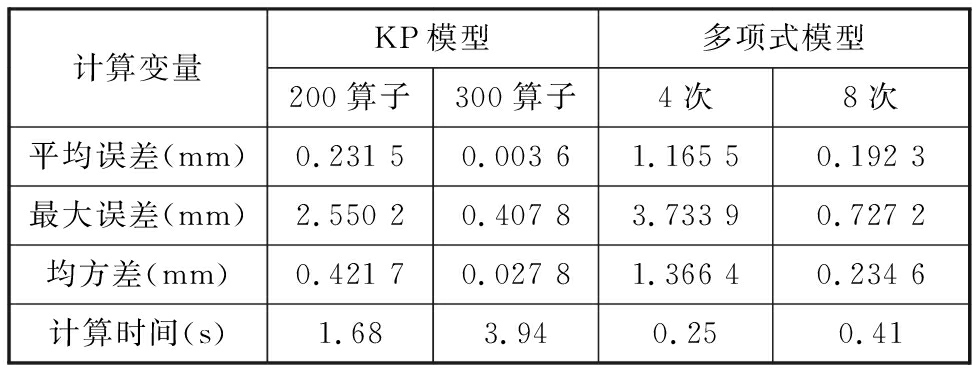
计算变量KP模型多项式模型200算子300算子4次8次平均误差(mm)0.231 50.003 61.165 50.192 3最大误差(mm)2.550 20.407 83.733 90.727 2均方差(mm)0.421 70.027 81.366 40.234 6计算时间(s)1.683.940.250.41
4 结论
(1)针对气动肌肉运动过程中的气压/位移迟滞非线性现象,本文分别采用KP模型与多项式模型对其位移/气压迟滞开展了建模研究,并采用最小二乘法对模型中的参数进行了辨识。
(2)随着KP算子个数的增加,KP模型的建模精度也随之显著提高,其计算时间也随之明显增加。
(3)多项式模型的建模精度随着多项式次数的增加而提高,其计算时间也随之增加,但是多项式次数不宜过高,以避免产生龙格现象而使多项式模型失效。
(4) 随着算子个数的增加,KP模型的建模精度显著高于多项式模型,但是其计算所耗费时间显著多于多项式模型,这是由于KP模型比多项式模型复杂,待辨识的参数也多于多项式模型。
[1] 谢胜龙,梅江平,刘海涛. McKibben型气动人工肌肉研究进展与趋势[J]. 计算机集成制造系统, 2018, 24(5): 1065-1081.
XIE Shenglong, MEI Jiangping, LIU Haitao. Achievements and Trends of Research on McKibben Pneumatic Artificial Muslcles[J]. Computer Integrated Manufacturing Systems, 2018, 24(5): 1065-1081.
[2] 施光林,沈伟. 气动人工肌肉并联平台自适应模糊CMAC姿态跟踪控制[J]. 中国机械工程, 2012, 23(2): 171-176.
SHI Guanglin, SHEN Wei. Adaptive Fuzzy CMAC Position Tracking Control of Parallel Platform Based on Pneumatic Artificial Muscles[J]. China Mechanical Engineering, 2012, 23(2): 171-176.
[3] 谢建蔚,陶国良,周洪.高速开关阀驱动的气动肌肉关节的滑模变结构跟踪控制[J]. 中国机械工程, 2007, 18(5): 540-544.
XIE Jianwei, TAO Guoliang, ZHOU Hong. Sliding Mode Tracking Control of Pneumatic Muscle Joint Actuated by High-speed On-Off Solenoid Valve[J]. China Mechanical Engineering, 2007, 18(5): 540-544.
[4] 王斌锐,周唯逸,许宏. 形状记忆合金编织网气动肌肉的驱动特性[J]. 中国机械工程, 2009, 20(4): 467-471.
WANG Binrui, ZHOU Weiyi, XU Hong. Actuating Characteristics of Pneumatic Muscle with Shape Memory Alloy Fiber Shell[J]. China Mechanical Engineering, 2009, 20(4): 467-471.
[5] 谢胜龙,刘海涛,梅江平,等. 气动人工肌肉迟滞-蠕变特性研究现状与进展[J]. 系统仿真学报, 2018, 30(3): 809-823.
XIE Shenglong, LIU Haitao, MEI Jiangping. Achievements and Developments of Hysteresis and Creep of Pneumatic Artificial Muscles[J]. Journal of System Simulation, 2018, 30(3): 809-823.
[6] 秦海辰,尹周平. 纯电力加载下压电陶瓷内环迟滞特性的实验研究[J]. 中国机械工程, 2014, 25(4): 517-521.
QIN Haichen, YIN Zhouping. Experimental Research of Minor-loop Hysteretic Behaviors of Piezoelectric Actuator under Pure Electrical Loading[J]. China Mechanical Engineering, 2014, 25(4): 517-521.
[7] MINH T V, TJAHJOWIDODO T, RAMON H, et al. A New Approach to Modeling Hysteresis in a Pneumatic Artificial Muscle Using the Maxwell-slip Model [J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(1): 177-186.
[8] MINH T V. Hysteresis Modelling and Control of an Antagonistic Manipulator Joint Actuated by Pneumatic Artificial Muscles[D]. Leuven,Belgium: University of Leuven, 2010.
[9] SCHREIBER F,SKLYARENKO Y, SCHLUTER K, et al. Tracking Control with Hysteresis Compensation for Manipulator Segments Driven by Pneumatic Artificial Muscles[C]//IEEE International Conference on Robotics and Biomimetics. Phuket: IEEE, 2011: 2750-2755.
[10] KOSAKI T, SANO M. Control of a Parallel Manipulator Driven by Pneumatic Muscle Actuators Based on a Hysteresis Model [J]. Journal of Environment and Engineering, 2011, 6(2): 316-327.
[11] KOSAKI T, MINESAKI A, SANO M. Adaptive Hysteresis Compensation with a Dynamic Hysteresis Model for Control of a Pneumatic Muscle Actuator [J]. Journal of Environment and Engineering, 2012, 7(1): 53-65.
[12] ITO A, KIYOTO K, FURUYA N. Motion Control of Parallel Manipulator Using Pneumatic Artificial Actuators[C]//IEEE International Conference on Robotics and Biomimetics. Tianjin: IEEE, 2010: 460-465.
[13] ZHOU M, WANG S, WEI G. Hysteresis Modeling of Magnetic Shape Memory Alloy Actuator Based on Krasnosel’skii-Pokrovskii Model[J]. The Scientific World Journal, 2013, 2013: 1-7.
[14] 于海涛,郭伟,谭宏伟,等.基于气动肌腱驱动的拮抗式仿生关节设计与控制[J]. 机械工程学报, 2012, 48(17): 1-9.
YU Haitao, GUO Wei, TAN Hongwei, et al. Design and Control on Antagonistic Bionic Joint Driven by Pneumatic Muscles Actuators[J]. Journal of Mechanical Engineering, 2012, 48(17): 1-9.
[15] XIE S L, MEI J P, LIU H T, et al. Motion Control of Pneumatic Muscle Actuator Using Fast Switching Valve [C]// ASIAN MMS 2016 & CCMMS 2016 Mechanism and Machine Science. Guangzhou: Springer, 2017: 1439-1451.
[16] 张桂林,张承进,李康. 基于PI迟滞模型的压电驱动器自适应辨识与逆控制[J]. 纳米技术与精密工程, 2013, 11(1): 85-89.
ZHANG Guilin, ZHANG Chengjin, LI Kang. Adaptive Identification and Inverse Control of Piezoelectric Actuators Based on PI Hysteresis Model[J]. Nanotechnology and Precision Engineering, 2013, 11(1): 85-89.
[17] 王湘江,王兴松. 基于KP模型的GMA迟滞系统辨识与补偿[J]. 中国机械工程, 2008, 19(10): 1167-1173.
WANG Xiangjiang, WANG Xingsong. GMA Hysteresis System Identification and Compensation Based on KP Model[J]. China Mechanical Engineering, 2008, 19(10): 1167-1173.
[18] XIE S L, LIU H T, MEI J P, et al. Modeling and Compensation of Asymmetric Hysteresis for Pneumatic Artificial Muscles with a Modified Generalized Prandtl-Ishlinskii Model[J]. Mechatronics, 2018, 52: 49-57.
