0 引言
纤维增强复合材料由于其高比强度、高比刚度等特性,被广泛应用在航天、航空、轨道交通等领域,并部分代替传统的金属结构材料。如美国波音787飞机的复合材料用量已达飞机结构用量的50%左右;国产高速列车的蒙皮也使用碳纤维/树脂复合材料,显示了这类材料巨大的应用前景。目前工程实际中,该类型材料被大量用来制成典型的复合薄板结构件,但是,随着结构形状越来越复杂、工作环境越来越恶劣和边界条件的多样化,其振动问题也越来越突出[1-3],常常会引发振动超标、疲劳失效等现象。特别是螺栓连接的部位,往往是整体系统的薄弱环节,一旦出现问题,将会导致整体结构的功能丧失,甚至酿成重大安全事故[4-5]。
目前,许多学者已经对纤维增强复合薄板、壳等结构件的固有特性问题开展了大量研究。例如,MOHAN等[6]采用伽辽金法求解了两端固支、固支-自由、四端简支3种边界下硼纤维/树脂复合薄板结构的固有频率和模态振型。SIVAKUMARAN[7]使用Rayleigh-Ritz能量法获得了复合材料薄板在自由边界条件下的固有频率和模态振型,主要考虑了薄板尺寸参数与纤维方向对固有频率的影响。LEISSA等[8]基于经典层合板理论计算了简支边界下石墨纤维/树脂复合材料薄板的固有频率,并讨论了层数与铺设角度对固有频率和模态振型的影响。杨杰等[9]基于子域分解技术、单向DQ离散格式和伽辽金法研究了其中一对边为混合型约束的矩形复合材料薄板的振动特性,但仅给出了固有频率的数值计算结果,并未开展测试验证。PELLICANO [10]则采用切比雪夫多项式法和谐波函数建立了两端固支和两端简支边界条件下复合薄壳的振型函数,并基于Sanders-Koiter理论分析了不同边界下结构的非线性振动问题。LIAO等[11]通过广义微分求积法研究了两端固支边界下纤维增强复合薄壳的固有特性问题。项爽[12]采用数值积分法研究了自由-简支、简支-简支两种边界条件下纤维增强复合薄壳固有特性的高效计算问题。漆文凯等[13]对悬臂和自由两种边界条件下的有损伤、无损伤的复合薄板进行了试验研究,讨论了不同边界下损伤位置和大小对固有特性的影响规律。史冬岩等[14]采用改进的傅里叶级数法分析了自由、固支等不同边界条件下正交各向异性薄板的振动特性,但仅获得了前6阶量纲一化频率参数,并未开展实验验证。王硕等[15]研究分析了周边固支和简支边界下,压电纤维复合板的固有频率随温度和电场的变化规律。
虽然已有众多学者对纤维增强复合薄壁构件的固有特性进行了大量研究,但是他们并没有进行实验验证,仅仅理论研究了固支、简支、自由等传统边界条件,螺栓松动边界条件对固有特性影响的文献则相对较少。因此,本文提出了人工弹簧刚度法来研究该问题,并将理论分析结果与测试结果进行了比较。
1 理论建模
本文研究的纤维增强复合薄板是由不用种类的基体材料以及具有各向异性特点的纤维组合压制而成,如图1所示。首先,将其中面作为参考平面,并建立oxyz坐标系。假设纤维方向与整体坐标系x轴方向的夹角为θ,薄板宽为b,薄板长为a,薄板厚为h,每一层位于z坐标轴较低表面hk-1和较高表面hk之间(k表示不同的纤维层),每层的厚度均相同。为了研究螺栓松动边界的影响,人为地在悬臂边界处引入多组弹簧,称之为人工弹簧刚度法,来模拟不同程度的螺栓松动边界。由于在该边界状态下,复合薄板的振动主要是横向弯曲振动,因此只需考虑结构沿z方向的移动刚度和绕x方向的扭转刚度。这里,假设Kcti代表移动约束弹簧刚度,而Kcri代表转动约束弹簧刚度。另外,假设1代表纤维纵向,2代表纤维横向,3代表垂直于1-2平面的方向,E1为纤维纵向对应的弹性模量,E2为纤维横向对应的弹性模量,G12为1-2平面对应的剪切模量,ν12为泊松比。
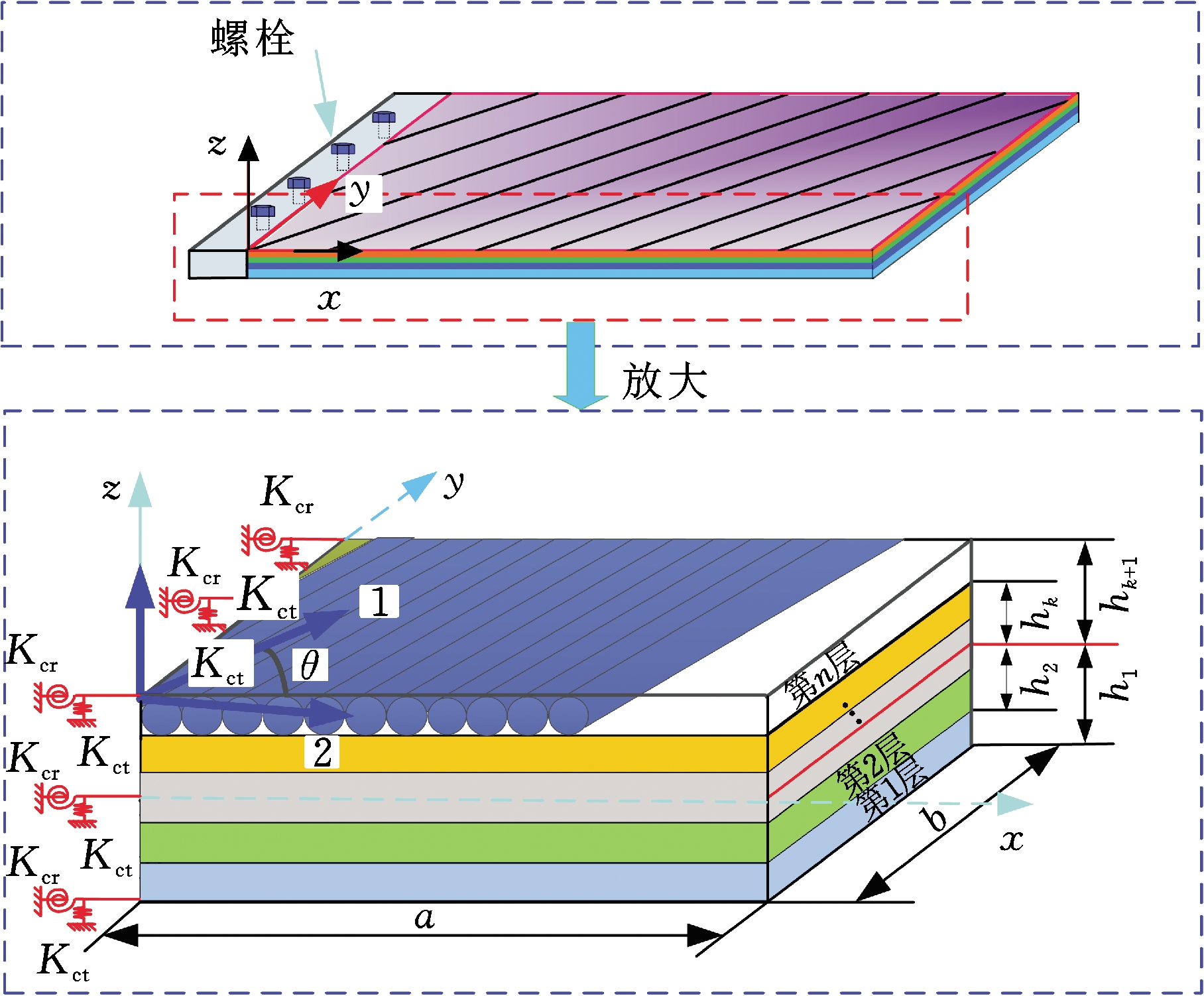
图1 螺栓松动边界下纤维增强复合薄板的理论模型
Fig.1 The theoretical model of fiber-reinforce composite plate under bolt loose boundary
由于复合薄板大多数为对称结构,其面内与横向振动之间不存在耦合关系,因此面内和面外位移是解耦的,根据小挠度薄板理论,将位移场写为如下形式:

(1)
式中,u(x,y,z,t)、v(x,y,z,t)、w(x,y,z,t)为板内任意一点的位移;u0、v0、w0为板的中面位移。
根据薄板理论,正应变和剪应变都为0,即εz=γyz=γxz=0,薄板内任意一点的位移和应变εx、εy、γxy可表示为

(2)
薄板中面弯曲挠曲率κx、κy和扭曲率κxy可表示为

(3)
εx=zκx εy=zκy γxy=zκxy
对于正交各向异性材料,纤维材料方向的应力-应变关系为

(4)
其中,Qij为不同的折减刚度系数;ε1、ε2、γ12为纤维材料方向的应变;ν12、ν21为由1、2方向引起的泊松比。
薄板所受的弯矩Mx、My和扭矩Mxy为

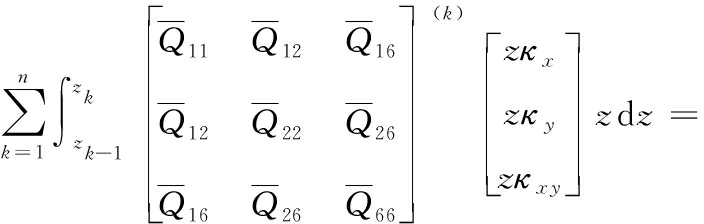
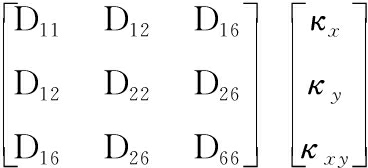
(5)
其中,σx、σy、σxy为薄板主轴方向的应力;n为纤维层数。薄板自由振动的动能可以用下式表示:
(6)
其中,ρ为薄板的密度;h为薄板的厚度;A为薄板的表面积。
薄板弯曲振动的应变能为
(7)
将式(3)和式(5)代入式(7)化简得
(8)
考虑螺栓松动边界影响后,储存在薄板结构约束端转动弹簧的应变能UR和移动弹簧的应变能UT分别为

(9)
![]()
Kct2![]() (w0(a,y,t))2dy++Kct3
(w0(a,y,t))2dy++Kct3![]() (w0(x,0,t))2dx+
(w0(x,0,t))2dx+
Kct4![]() (w0(x,b,t))2dx]
(w0(x,b,t))2dx]
(10)
其中,Kcr2、Kcr3、Kcr4、Kct2、Kct3、Kct4均等于零。
假设振动的位移形式为
w0(x,y,t)=W(x,y)eiωt
(11)
其中,W(x,y)为振型函数;ω为固有圆频率。由Ritz法可得中面位移有如下形式:
(12)
式中,cij为未知系数;pi(x)和qj(y)为一系列的正交多项式。
为了得到一系列的正交多项式,对约束端的多项式函数进行正交化处理:
pi(x)=(x-Ai)pi-1(x)-Bipi-2(x)
(13)

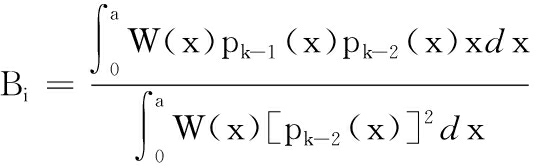
其中,i≥2;W(x)为权函数,通常取W(x)=1,同时定义p0(x)=0。
同样采用上述方法构造正交多项式qj(y)。我们定义这一系列正交函数的首项为
p1(x)=1 q1(y)=1
将式(11)代入式(6)、式(8)、式(9)和式(10)中,可以得到薄板自由振动的最大动能UKmax、薄板弯曲振动的最大应变能UPmax分别为
考虑螺栓松动边界影响后,储存在转动弹簧内的最大应变能URmax和移动弹簧内对应的最大应变能UTmax可分别表示为
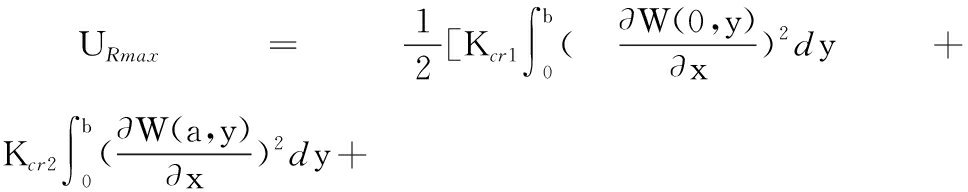
![]()
Kct3![]() (W(x,0))2dx+Kct4
(W(x,0))2dx+Kct4![]() (W(x,b))2dx]
(W(x,b))2dx]
机械系统总体的最大应变能为
Umax=UPmax+URmax+UTmax
(14)
薄板自由振动总体的能量函数可表达为
L=Umax-UKmax
(15)
由于解析法很难得到该边界下复合薄板的精确解,因此本文采用Ritz近似解法以及哈密顿原理求解,得到
![]() =0 i=1,2,…,M; j=1,2,…,N
=0 i=1,2,…,M; j=1,2,…,N
(16)
其中,待定参数cij是薄板能量函数中的未知系数。将式(15)代入式(16)中,得到M×N个齐次线性代数方程,整理得到以下矩阵形式:
(K-ω2M)q=0
(17)
其中,K和M分别为该系统的对称刚度矩阵和质量矩阵,q为特征向量,q=(c11,c12,…,c1N)。因为式(17)有解,所以
det(K-ω2M)=0
(18)
最终,通过式(18)可求得各阶模态对应的固有频率值,然后将固有频率代入式(17)得到特征向量q,将q代入振型函数(式(12)),即可获得复合薄板的模态振型。在式(12)中,M、N值越大,求得的固有频率值就越精确,一般取M=N=8即可达到要求的精度。
2 计算流程
计算螺栓松动边界下复合薄板固有频率和模态振型的流程可分为如下步骤。
(1) 输入复合薄板几何参数与材料参数。首先输入复合薄板的宽度、厚度、长度以及每层纤维角度等几何参数;然后,输入纤维纵向和纤维横向的剪切模量、泊松比、弹性模量和密度等材料参数。
(2) 计算与人工弹簧移动和转动相对应的薄板弯矩与扭矩。基于经典层合板理论,将式(3)代入式(5)计算出与人工弹簧移动刚度Kct和转动刚度Kcr对应的薄板弯矩与扭矩。
(3) 基于正交多项式法计算薄板的最大动能、弯曲应变能和储存在弹簧中的应变能。根据弹性体动力学原理,将式(11)代入式(6)、式(8)、式(9)和式(10)中,获得薄板自由振动的最大动能UKmax、薄板弯曲振动的最大应变能UPmax以及人工弹簧所储存的最大应变能UTmax+URmax。
(4) 在不同的弹簧刚度下求解固有频率和模态振型,并分析松动边界对固有特性的影响。将步骤(3)中获得的UKmax、UPmax、URmax、UTmax代入式(15)中,可以计算获得能量函数L的表达式。采用Ritz法可求解得到纤维增强复合薄板的固有频率。将各阶固有频率所对应的特征向量q=(c11,c12,…,c1N)代入振型函数(式(12))中,即可得到各阶模态振型W(x,y)。最后,通过改变弹簧刚度的大小来详细研究螺栓松动边界对结构固有频率和模态振型的影响。图2给出了该类型边界条件下复合薄板固有特性的计算流程。

图2 螺栓松动边界条件下复合薄板固有特性的计算流程
Fig.2 Calculation procedure of inherent characteristics of fiber-reinforce composite plate under bolt loose boundary
3 实验验证
为了验证本文所提出的理论方法的正确性,以HF10碳纤维/树脂基复合薄板为研究对象,搭建了图3所示的基于预埋压力传感器的螺栓松动边界下的实验系统来测试其固有频率和模态振型。该类型复合薄板为对称正交铺设,即[(90°/0°)590°/0°/90°(0°/90°)5],共有23层,每个铺层具有相同的纤维体积分数和厚度,宽度、长度、厚度分别为260 mm、100 mm、2.60 mm,E1=136 GPa,E2=7.92 GPa,G12=3.39 GPa,ν12=0.32,质量为110.7 g,密度ρ=1 638 kg/m3。

图3 螺栓松动边界条件下纤维增强悬臂复合薄板振动测试系统
Fig.3 The vibration test system of fiber-reinforced composite plate under bolt loose boundary
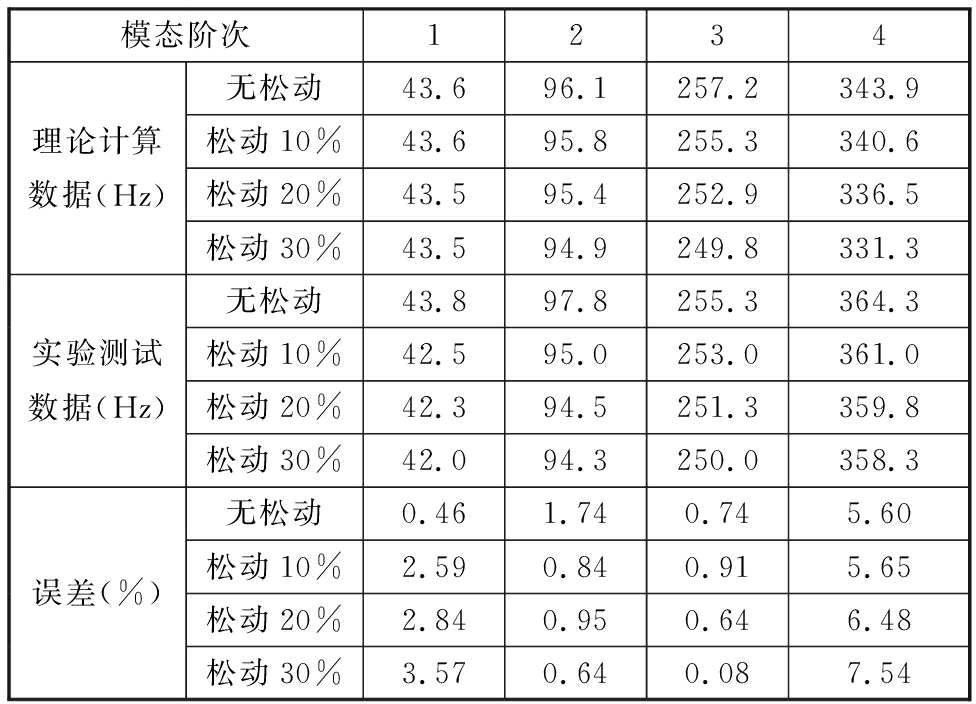
首先,通过预埋的方式将压力传感器用2组M12螺栓安装到图3所示的夹具中,夹紧复合薄板的一侧,并通过LMS数据采集仪和笔记本工作站记录螺栓无松动状态下预埋压力传感器对应的压力值。然后,开展扫频测试,利用激光测振仪和激光线性扫描系统获得该边界条件下复合薄板的各阶固有频率,同时利用激光扫描法[16]依次获得各阶模态振型。最后,松动螺栓从而改变压力传感器的压力值,使其分别达到无松动边界下的90%、80%和70%,即分别在螺栓松动10%、20%和30%这3种边界条件下,重复测试各阶固有频率和振型。表1和表2分别给出了上述螺栓松动边界条件下测试获得的悬臂复合薄板的前4阶固有频率和模态振型。为了方便比较,将基于人工弹簧刚度法获得的理论计算结果也一并列入表1和表2中。
分析上述结果可知,螺栓松动边界条件下复合薄板固有频率的测试结果与计算结果的误差在0.08%~7.54%之间,属于误差允许的范围,且两者的振型形态也基本一致,进而验证了理论计算方法的正确性。本文所提出的方法普遍适用于螺栓松动边界条件下该类型复合薄板固有特性的分析与计算。
表1 理论计算和测试获得的螺栓松动边界条件下复合薄板前4阶固有频率
Tab.1 The first 4 natural frequencies of the composite plate obtained by theoretical calculation and test under the bolt loose boundary
模态阶次1 234理论计算数据(Hz)无松动43.696.1257.2343.9松动10%43.695.8255.3340.6松动20%43.595.4252.9336.5松动30%43.594.9249.8331.3实验测试数据(Hz)无松动43.897.8255.3364.3松动10%42.595.0253.0361.0松动20%42.394.5251.3359.8松动30%42.094.3250.0358.3误差(%)无松动0.461.740.745.60松动10%2.590.840.915.65松动20%2.840.950.646.48松动30%3.570.640.087.54
表2 理论计算和测试获得的螺栓松动边界条件下复合薄板前4阶模态振型
Tab.2 The first 4 modal shapes of the composite plate obtained by theoretical calculation and test under the bolt loose boundary
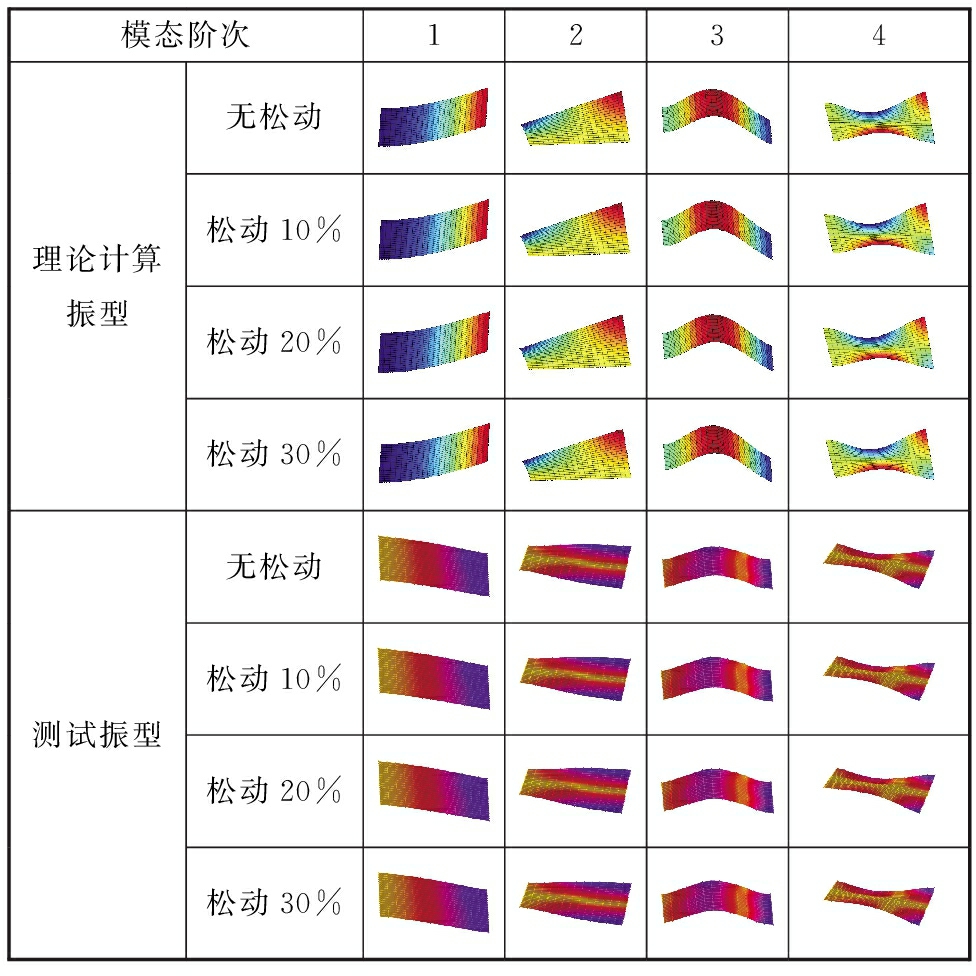
模态阶次1234理论计算振型无松动松动10%松动20%松动30%测试振型无松动松动10%松动20%松动30%
4 结论
本文主要研究了螺栓松动边界下纤维增强复合薄板固有特性的分析方法,并进行相应的实验。
(1)基于人工弹簧刚度法、经典板壳理论,通过Ritz法推导出n层纤维增强复合薄板的动能、最大应变能及人工弹簧移动和转动方向的最大应变能,进而求解出螺栓松动边界下纤维复合薄板的前4阶固有频率。
(2) 以HF10碳纤维/树脂复合薄板为研究对象,测试获得了螺栓松动边界下薄板的前4阶固有频率和振型。经过与理论计算的相应结果对比发现,两者的振型形态基本一致,其固有频率的误差处于允许范围内,说明本文方法的正确性。
[1] MALLICK P K. Fiber-reinforced Composites: Materials, Manufacturing, and Design[M]. CRC press, 2007:3-15.
[2] 沈观林. 复合材料力学[M].北京: 清华大学出版社, 2006:1-25.
SHEN Guanlin. Mechanics of Composite Materials[M]. Beijing:Tsinghua University Press, 2006:1-25.
[3] 齐红宇, 温卫东, 崔海涛. 含孔复合材料层合板疲劳寿命预测研究[J]. 航空动力学报, 2003, 18(5):658-661.
QI Hongyu, WEN Weidong, CUI Haitao. Fatigue Life Predication of Notched Composite Material Laminates[J]. Journal of Aerospace Power, 2003, 18(5):658-661.
[4] KAWA K. Mechanics of Composite Materials[M]. Boca Raton: The Chemical Rubber Company Press, 2005:5-28.
[5] 徐颖, 温卫东, 崔海涛. 复合材料层合板疲劳逐渐累积损伤寿命预测方法[J]. 航空动力学报, 2007, 22(4):602-607.
XU Ying, WEN Weidong, CUI Haitao. Progressive Fatigue Damage Analysis Method of Laminated Composites[J]. Journal of Aerospace Power, 2007, 22(4):602-607.
[6] MOHAN D, KINGSBURY H B. Free Vibrations of Generally Orthotropic Plates[J]. Journal of the Acoustical Society of America, 1971, 50(1):266-269.
[7] SIVAKUMARAN K S. Natural Frequencies of Symmetrically Laminated Rectangular Plates with Free Edges[J]. Composite Structures, 1987, 7(3):191-204.
[8] LEISSA A W, NARITA Y. Vibration Studies for Simply Supported Symmetrically Laminated Rectangular Plates[J]. Composite Structures, 1989, 12(2):113-132.
[9] 杨杰, 彭建设. 面内荷载作用下混合型边界约束复合材料层合板的振动特性[J]. 强度与环境, 2001(1):26-31.
YANG Jie, PENG Jianshe. Vibration Analysis of Composite Laminate Plates with Mixed Edge Boundary Constraints and In-plane Loading[J]. Strength and Environment, 2001(1): 26-31.
[10] PELLICANO F. Vibrations of Circular Cylindrical Shells: Theory and Experiments[J]. Journal of Sound & Vibration,2007,303(1/2):154-170.
[11] LIAO C L, CHENG C R. Dynamic Stability of Stiffened Laminated Composite Plates and Shells Subjected to In-plane Pulsating Forces[J]. Journal of Sound and Vibration, 1994, 174(3): 335-351.
[12] 项爽.旋转功能梯度材料圆柱壳的振动特性研究[D].洛阳:河南科技大学,2013.
XIANG Shuang. Free Vibration of Rotating Functionally Graded Cylindrical Shells[D]. Luoyang:Henan University of Science and Technology, 2013.
[13] 漆文凯, 程博, 刘磊. 复合材料层合板的振动模态试验研究[J]. 航空发动机, 2013, 39(6):53-58.
QI Wenkai, CHENG Bo, LIU Lei. Research of Vibration Modal Experiment for Composite Laminates[J]. Aeroengine, 2013, 39(6):53-58.
[14] 史冬岩, 王青山, 石先杰,等. 任意边界条件下正交各向异性薄板自由振动特性分析[J]. 上海交通大学学报, 2014, 48(3):434-438.
SHI Dongyan, WANG Qingshan, SHI Xianjie, et al. Free Vibration Analysis of Orthotropic Thin Plates in General Boundary Conditions [J]. Journal of Shanghai Jiao Tong University, 2014, 48(3):434-438.
[15] 王硕,滕兆春.加热压电纤维复合材料圆板的横向自由振动[J].计算力学学报, 2017, 34(3):286-291.
WANG Shuo, TENG Zhaochun . Transverse Free Vibration of Heated Piezoelectric Fibre Composite Materials Circular Plates[J]. Chinese Journal of Computational Mechanics, 2017, 34(3):286-291.
[16] 常永乐, 李晖, 杨雪峰, 等. 纤维增强复合薄板非线性振动测试平台开发及应用[J]. 中国工程机械学报, 2017(2): 147-152.
CHANG Yongle, LI Hui, YANG Xuefeng, et al. Development and Application of Npnlinear Vibration Testing Platform for Fiber Reinforced Composite Thin Plate[J]. Chinese Journal of Constructive Machinery, 2017(2): 147-152.
