0 引言
国际制造业竞争日益激烈,对先进制造技术的需求更加迫切,以“德国工业4.0”为代表的智能化技术革命推动传统制造向智能制造转型,不仅要建设智能工厂和智慧车间,而且要实现智能仓储和智能物流。在企业仓储作业中,订单拣选一直被认为是最消耗成本和劳动力的一环,约55%的仓库运营成本用于这一过程[1]。在订单拣选过程中,订单服务时间是衡量仓库作业效率的重要指标,而订单服务时间与行走距离紧密相关[2]。影响行走距离的几大因素主要包括:仓库大小及布局[3-4]、作业策略(如按订单拣选或按批次拣选)[5-6]、存储分配策略[7]、分区拣选策略[8]和路径策略[9]。合理设计和管理这些影响因素都有助于减少行走距离。然而,由于影响因素相互制约,同时优化多个影响因素比较困难,大多数研究是分析并优化某一特定影响因素[10]。因其灵活性,路径策略被认为具有更大的动态调整潜力[11],运用专业的启发式路径策略可以显著减少拣货员的行走距离,然而现实中大多数仓库仍然采用人工经验式路径策略[12]。本文选取路径策略作为优化对象,以降低作业成本、缩短订单响应时间,进而提升仓储运作的智能化水平。
仓储拣选路径优化问题可抽象为特殊的TSP(traveling salesman problem)问题。对于这类问题,精确算法只能应用于问题规模较小的情况。随着问题规模的扩大,问题的复杂度呈指数上升,精确算法显得无能为力,而元启发式算法(遗传算法、蚁群算法、模拟退火算法等)能够在允许时间内找到问题的最优解或接近最优解。陈呈频等[13]为解决车辆路径问题提出了多染色体遗传算法,该算法呈现出搜索效率高和收敛速度快的特点。高海昌等[14]分析了多种智能优化算法求解TSP问题的优缺点和改进策略,给出了求解TSP问题的研究方向及建议。王宏等[15]设计了一种遗传算法用于解决传统仓库拣货路径优化问题,优化效果明显。
目前传统布局仍广泛存在于实际仓库中[16],然而GUE等[17]通过放松约束条件,提出了两种新的布局:flying-V和鱼骨(fishbone)布局,证明了在总货位数量相等的条件下,相比于传统布局,两种新布局能使拣货员从P&D (pickup and deposit)点到单个货位的平均距离分别减少约10%和20%。
现有经典常用的仓储拣选算法包括S-Shape、Largest Gap和Midpoint等[18],例如S-Shape算法规则是当一个通道中有待拣选货位时,拣货员就穿过该通道,不含待拣选货位的通道则不进入,直至完成订单中最后一个待拣选货位后返回出发点。这些经典算法可以降低拣选错误发生的概率,在人工经验管理业务方式下往往容易被配送中心采用。但是人工经验路径方法一般不是最优的路径策略[19],而且不符合当前仓储管理的智能化和精益化发展趋势。国内外学者开展了拣货路径的新型智能算法研究[20-22],并以常用的S-Shape算法作为衡量新算法性能的基准。
本文针对fishbone非传统布局的特点,建立订单拣选路径优化模型,并设计一种多种群遗传算法(multiple population genetic algorithm,MPGA)用于求解该模型。为验证算法的有效性,进行了一系列仿真实验,验证MPGA算法在不同拣货数量下的性能表现,并选取了S-Shape算法和标准遗传算法(standard genetic algorithm,SGA)作对比。
1 布局与模型
1.1 鱼骨布局结构
传统布局、flying-V布局和fishbone布局3种仓储布局的结构图见图1。该fishbone仓储布局分为4个拣货区,如图2所示,货区编号从仓库左下角开始,顺时针依次为①、②、③、④。布局主要由斜主通道、前后主通道、左右主通道、拣货通道和货位组成。该布局基于以下假设:①存在单个P&D点位于仓库前端中心;②同一拣货通道中左右两侧货物拣选时行走的距离忽略不计;③拣货通道两端均可进入,并且允许在通道内折回;④每个货位的几何尺寸一致。
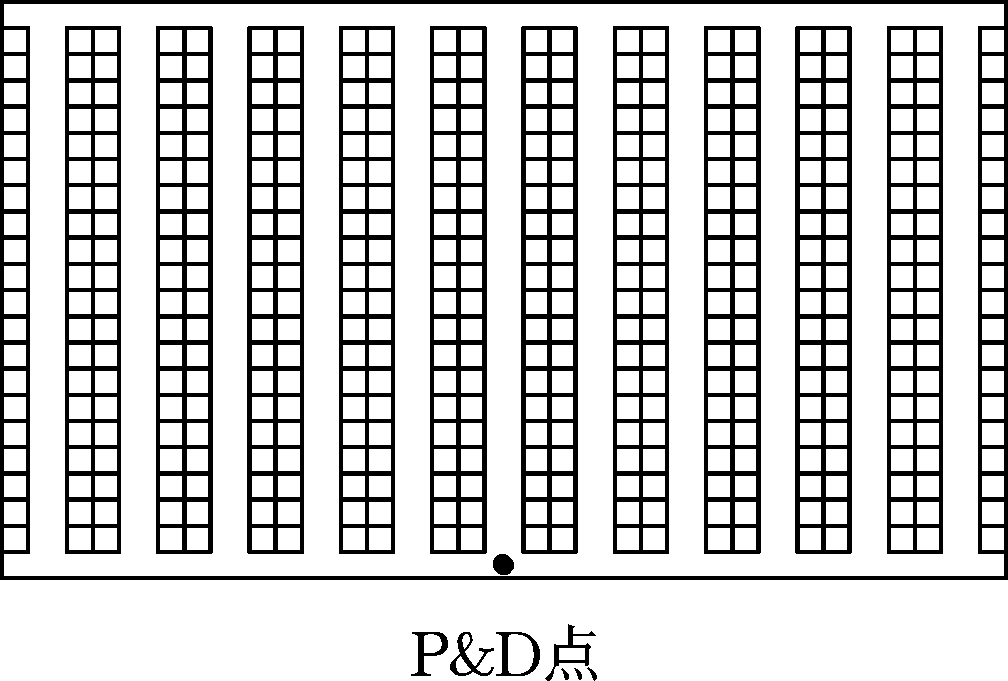
(a) 传统布局

(b) flying-V布局
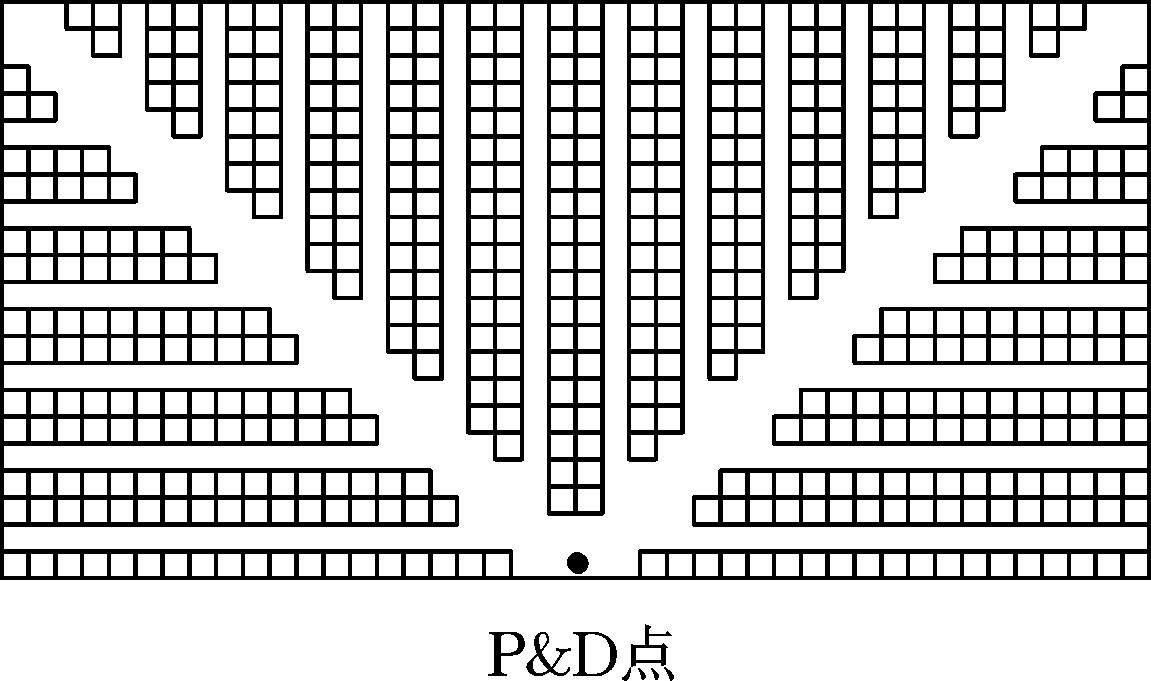
(c) 鱼骨布局
图1 三种仓储布局结构图
Fig.1 Three layouts structure diagram of warehouse
1.2 布局参数设计
货位长和宽设为e,拣货通道、前后主通道和左右主通道的宽度也设为e,斜主通道的宽度设为2e。k(k=1,2,3,4)表示货区号,x(x=1,2,…,xmax)表示货架的排数,y(y=1,2,…,ymax)表示货架列数。图2中标明了各区货架排和列的编号顺序,因而布局中的每个货位都有唯一的编码,P&D点记为(0,0,0),其他位于k区x排y列的货位记为(k,x,y),如(2,5,4)表示位于2区5排4列。
1.3 建立拣选路径优化模型
参数说明:N为待拣选点的数目;i,j为待拣选点集合中的任意拣选点;dij为任意拣选点i,j之间的距离;d01为第一个拣选点到P&D点的距离;dN0为最后一个拣选点到P&D点的距离。
Uij为决策变量,在访问完拣选点i之后是否前往拣选点j;拣选路径优化模型如下:
(1)
约束条件:
(2)
(3)
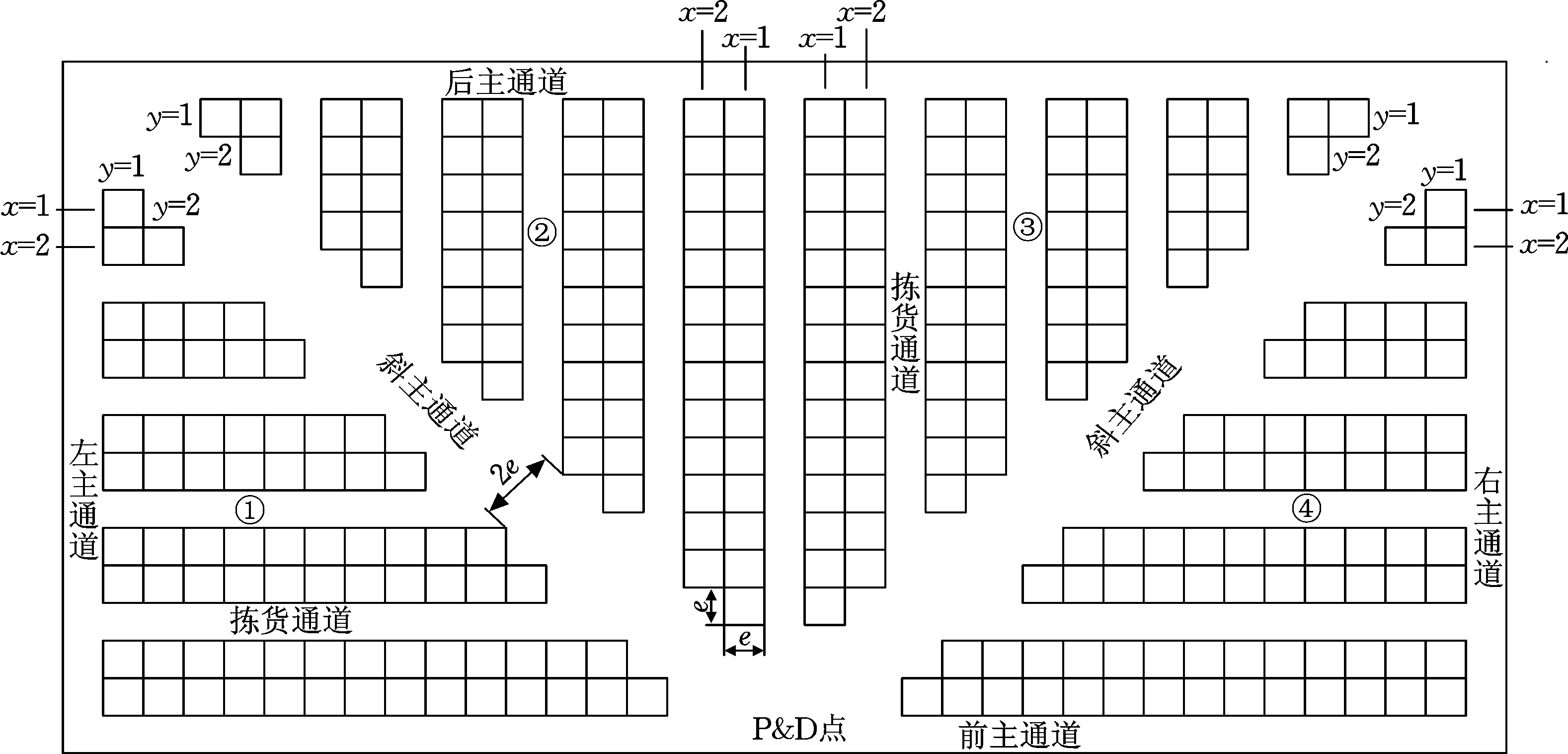
图2 鱼骨布局
Fig.2 Fishbone layout
(4)
目标函数式(1)表示访问完所有拣选点后,总的拣选距离最小;约束条件式(2)和式(3)表示每个待拣选点只能被拣选一次;约束条件式(4)为决策变量的取值,如果完成i点的拣选任务后立即前往j点则取值为1,否则取值为0。
1.4 建立非传统货位距离矩阵
鱼骨布局属于非传统布局,故传统布局下的任意两个拣选点之间的距离计算公式不再适用于非传统布局,因此,构建非传统布局下的货位距离矩阵是解决该路径优化问题的关键内容之一。POHL等[23]分析了fishbone布局下任意两货位点间的可能路径,本文在此基础上求出了任意两货位点之间的距离。任意两点间的距离计算分为两种情况:同区货位之间的距离和不同区货位之间的距离。式(5)~式(13)是两种情况的距离公式,根据布局的对称性,两货位在③④区和②④区的距离公式可分别参照①②区和①③区,距离公式中的参数说明见表1。图3是仅绘制通道的布局简图,在图中标明了距离公式的参数。
表1 距离公式参数说明
Tab.1 Explanation of distance formula parameters

参数含义Ai拣选点i所在通道号Si拣选点i到通道起始端的距离Li拣选点i所处通道的长度rt 第t(t=1,2,3,…)条路线lrt路线rt的长度a相邻拣货通道间的距离b相邻拣货通道截斜主通道的长度v拣货通道转至前后主通道或左右主通道消耗的距离ω拣货通道转至斜主通道消耗的距离

图3 鱼骨布局简图
Fig.3 Simplified diagram of fishbone layout
同区货位的路线如图4所示。其中,r1代表P&D点与货位的路线,r2代表两货位位于同区同一通道的路线,r3和r4代表两货位位于同区不同通道的路线。
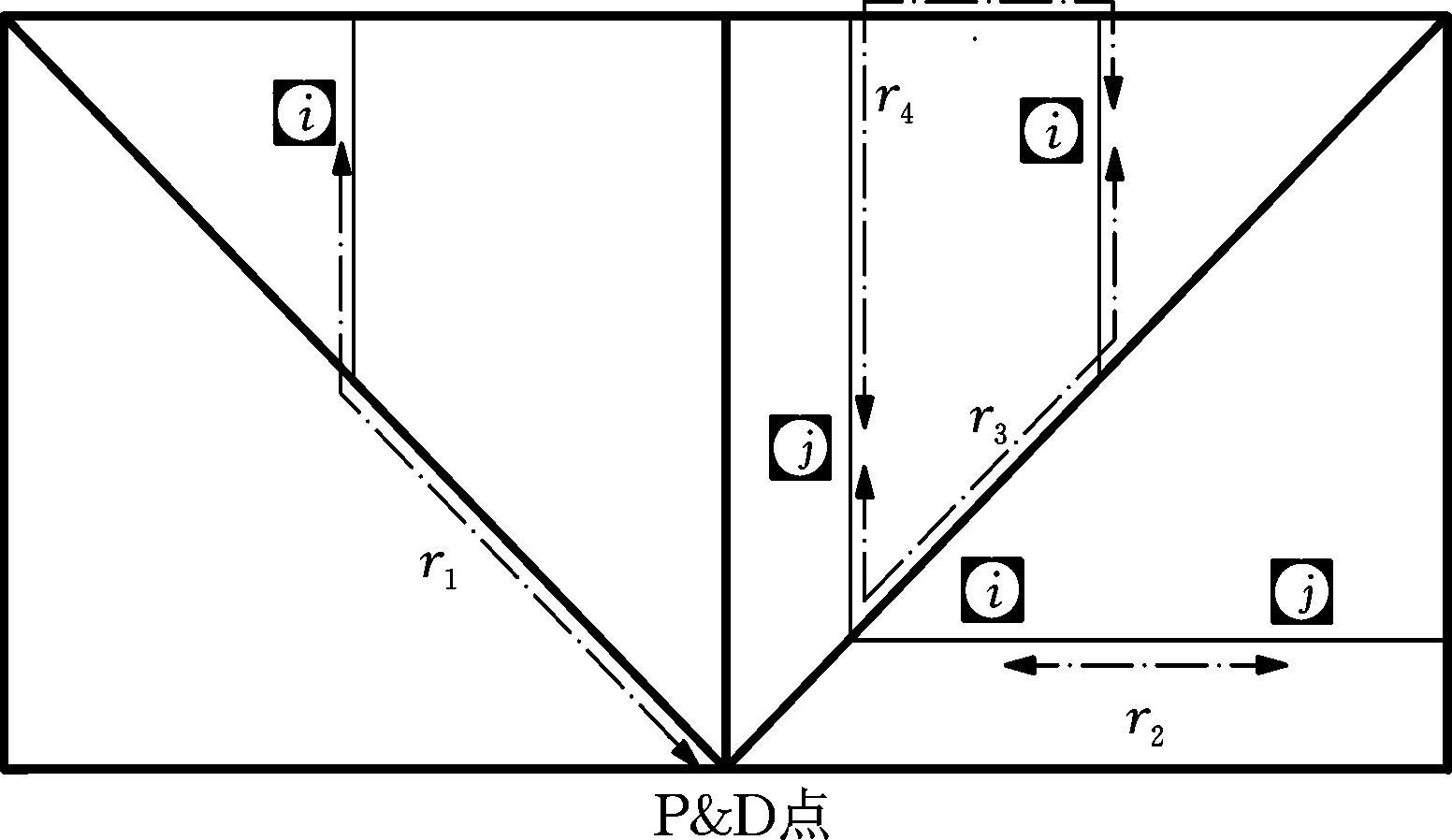
图4 同区的路线图
Fig.4 Routes in the same region
P&D点与货位的距离
d01=lr1=Li-Si+ω+bAi
(5)
两货位位于同区同一通道的距离
dij=lr2=Si-Sj
(6)
两货位位于同区不同通道的距离
(7)
两货位位于①②区和两货位位于②③区的路线如图5所示,其中,r5代表①②区两货位通道号相同的路线,r6和r7代表①②区两货位通道号不同的路线,r8代表②③区两货位通道号同时为0的路线,r9和r10代表②③区两货位通道号不同时为0的路线。

图5 ①②区、②③区的路线图
Fig.5 Routes in region ①② and region ②③
①②区两货位通道号相同的距离
dij=lr5=Li+Lj-Si-Sj+2ω
(8)
①②区两货位通道号不同的距离
dij=min(lr6,lr7)
(9)
lr6=Li+Lj-Si-Sj+2ω+b(Ai-Aj)
lr7=2Li-Si+Sj+2ω+2v+a(Ai-Aj)
②③区两货位通道号同时为0的距离
dij=lr8=Sj-Si
(10)
②③区两货位通道号不同时为0的距离
dij=min(lr9,lr10)
(11)
lr9=Li+Lj-Si-Sj+2ω+b(Ai+Aj)
lr10=Si+Sj+2v+a(Ai+Aj)
两货位位于①③区和两货位位于①④区的路线如图6所示,其中,r11和r12代表两货位位于①③区的路线,r13和r14代表两货位位于①④区的路线。
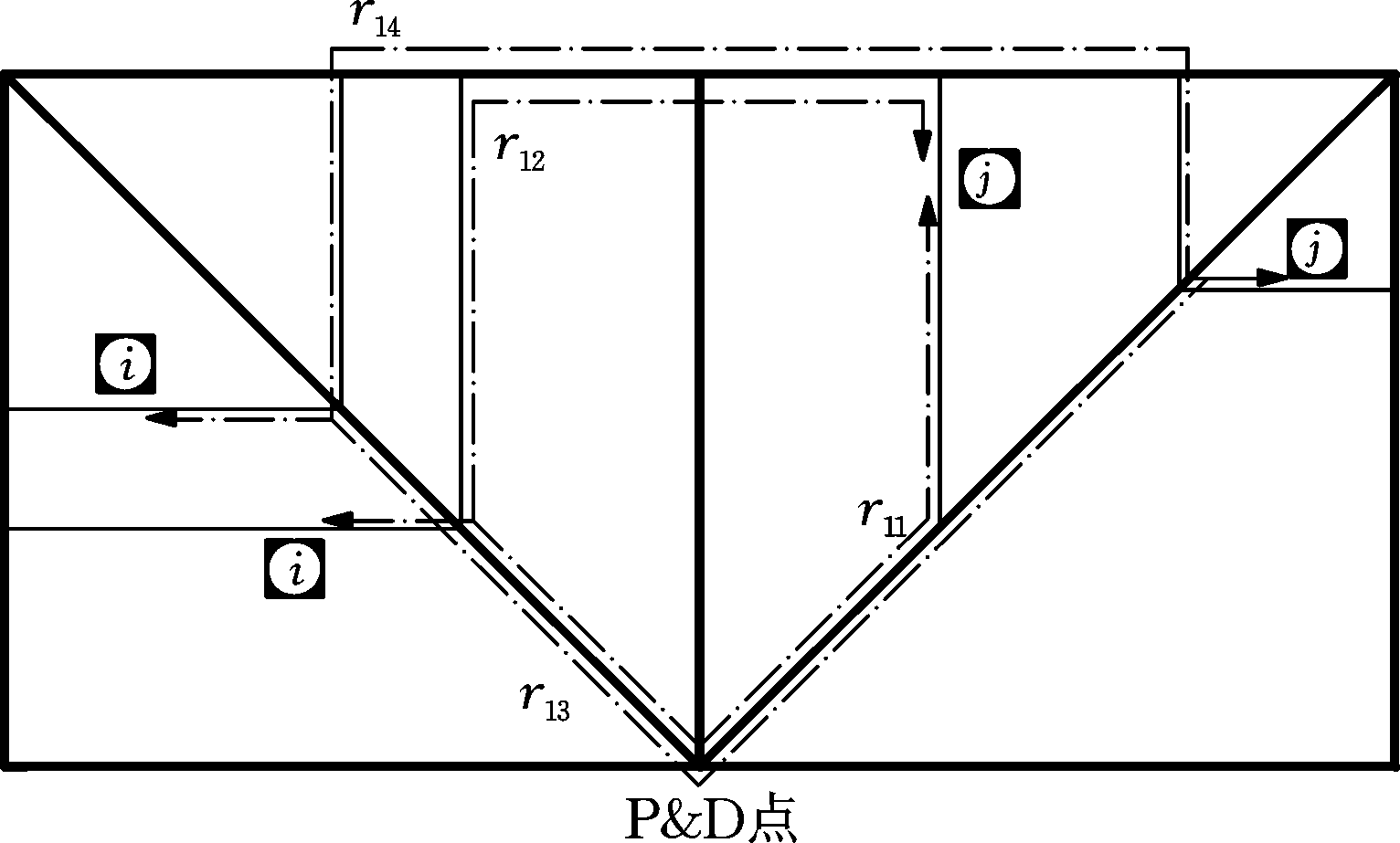
图6 ①③区、①④区的路线图
Fig.6 Routes in region ①③ and region ①④
两货位位于①③区的距离
dij=min(lr9,lr10)
(12)
lr11=Li+Lj-Si-Sj+2ω+b(Ai+Aj)
lr12=2Li-Si+Sj+2ω+2v+a(Ai+Aj)
两货位位于①④区的距离
dij=min(lr9,lr10)
(13)
lr13=Li+Lj-Si-Sj+2ω+b(Ai+Aj)
lr14=2Li+2Lj-Si-Sj+4ω+2v+a(Ai+Aj)
2 算法设计
遗传算法(GA)是一种仿效生物界中“物竞天择、适者生存”法则的随机搜索算法,非常适用于处理传统搜索算法难以解决的复杂优化问题[24-25]。遗传算法采用选择、交叉和变异算子进行搜索,全局搜索能力较强,但局部搜索能力较弱。此外,遗传算法还易出现未成熟收敛现象。多种群遗传算法(MPGA)可以用来取代常规的标准遗传算法(SGA)[26],为了进一步优化多种群遗传算法的性能,本文引入了进化逆转算子来解决非传统布局下的拣选路径优化问题。进化逆转算子是仿造遗传学中的倒位现象,在染色体中存在基因位置是倒转的两点,使得在父代中距离很远的基因位在后代中紧靠在一起,使得染色体位串上的重要基因更加紧凑,不容易被交叉算子分开,进而提高算法的局部搜索能力。
2.1 算法流程
MPGA在SGA的基础上加入了进化逆转算子并将其扩展到多个种群,移民算子使各种群能相互联系,人工选择算子能保存各种群每代中的最优个体。SGA的算法流程图和MPGA的算法结构示意图见图7、图8。

图7 SGA算法流程图
Fig.7 Flowchart of SGA
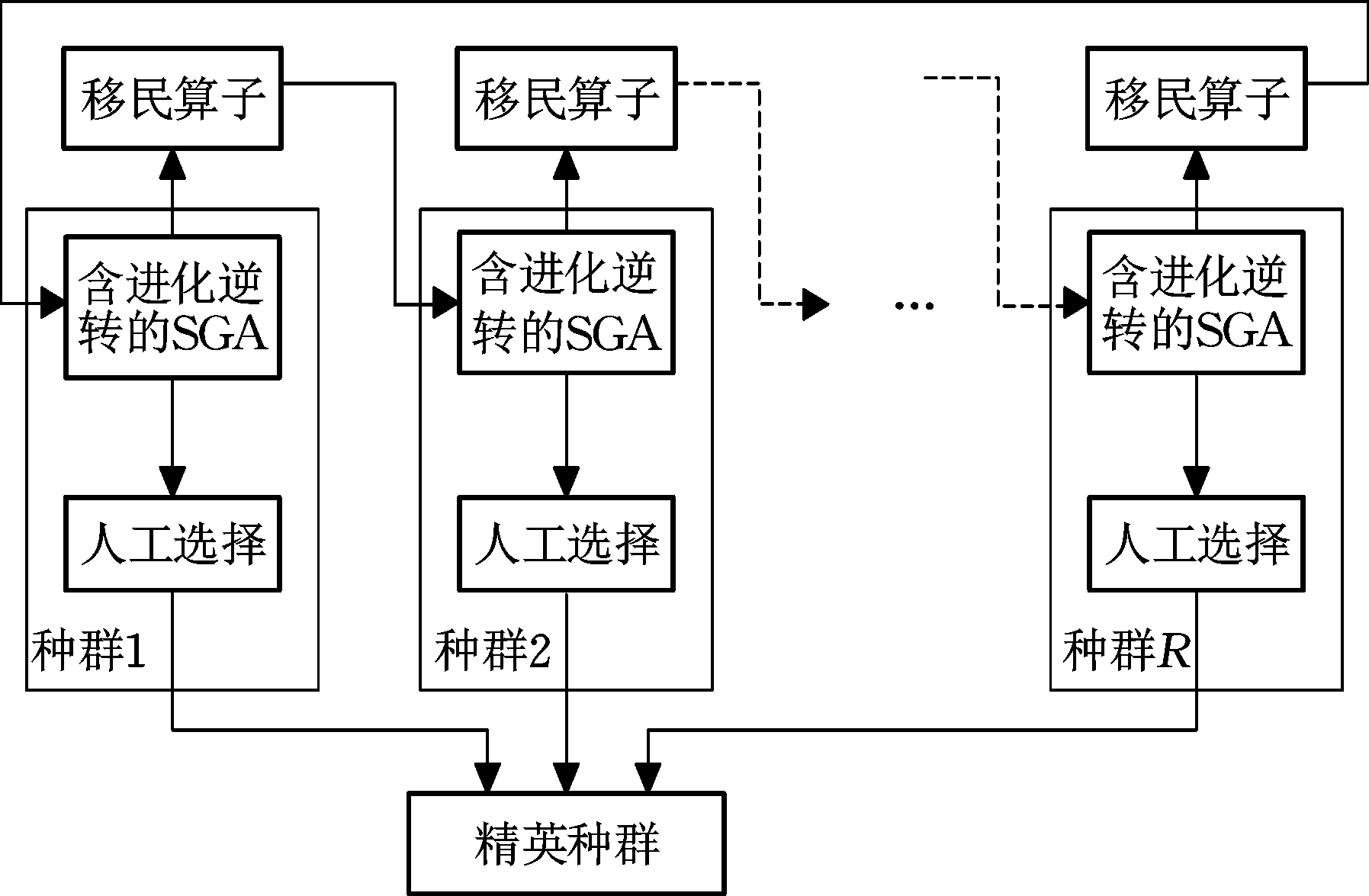
图8 MPGA算法结构示意图
Fig.8 Structure schematic diagram of MPGA
2.2 算法实现
(1)编码。对于拣选路径优化问题,整数排列编码是最自然、合理的编码方式。将随机产生的待拣选点依次进行序列编号,然后用编号的先后顺序来表示拣选路径。假设现有一个包含5个待拣选物品的订单,采用1,2,…,5依次表示5个物品在仓库中的位置编号,0表示P&D点的位置,那么序列0|4|2|1|3|5|0就是一个合法的染色体,表示的拣选路径为P&D点→货物4→货物2→货物1→货物3→货物5→P&D点。
(2)种群初始化。染色体编码完成后,产生R个种群,每个种群包含M个个体。
(3)适应度函数。适应度函数为拣货员在完成一次订单拣货作业总行走距离的倒数,即个体的适应度为VFit=1/f,其中VFit为个体适应度值,f为目标函数。优化的目标就是选择适应度值大的个体,淘汰适应度值小的个体,适应度值越大表明个体越优质。
(4)选择算子。选择算子是从旧群体中以一定的概率选择个体到新群体中,个体被选中的概率和适应度值有关,个体适应度值越大,被选中的概率越大,采用随机竞争选择策略。
(5)交叉算子。交叉算子决定算法的全局搜索能力,各种群取不同的交叉概率,其值Pc=0.7+(0.9-0.7)rand(R,1)。采用部分映射杂交策略,确定交叉操作的父代,将父代两两分组,每组重复以下过程(假定待拣选货位数为10):①产生两个[1,12]区间内的随机整数c1和c2,确定两个位置,对两位置的中间数据进行交叉,如c1=5,c2=9,
09513742108600105463872190
交叉为
0951638710**00105*3742*190
②交叉后,同一个体中不重复的数字保留,有重复的数字(带*位置)采用部分映射的方法消除重复,即利用中间段的对应关系进行映射。结果为
09516387104200105837426190
(6)变异算子。变异算子决定了算法的局部搜索能力,各种群取不同的变异概率,其值为Pm=0.01+(0.05-0.01)rand(R,1),变异策略采取随机选取两个点,将其对换位置。为改善遗传算法的局部搜索能力,在选择、交叉、变异之后引进了进化逆转算子。这里的“进化”是指逆转算子的单方向性,即只有逆转后适应度值有提高的才接受,否则逆转无效。产生两个[1,12]区间内的随机整数c1和c2,确定两个位置,将c1,c2内的数字对换位置,如c1=5,c2=9,
0951738610420
进化逆转后为
0951683710420
(7)移民算子。各个种群之间通过移民算子进行联系,实现多种群的协同进化。实现种群之间的信息交换的具体操作规则是,在每次迭代进化过程中,将目标种群中的最差个体用前一个种群的最优个体代替。
(8)人工选择算子。在进化的每一代中,通过人工选择算子选出其他种群的最优个体放入精英种群加以保存。精英种群不进行选择、交叉、变异等遗传操作,保证进化过程中各种群产生的最优个体不被破坏和丢失。
(9)算法终止条件。采用双重优先终止机制,即达到最大遗传代数Gmax或达到最优个体最少保持代数Gmin时算法终止。
3 仿真实验
3.1 实验参数设定
仿真实验基于图2中的fishbone布局,该布局共有300个货位和一个位于仓库前端中心的P&D点,设货位的长宽e=1,通过布局的几何关系得到![]() 每个货区的通道0、通道1、通道2、通道3、通道4、通道5的长度分别为15.5,12.5,9.5,6.5,3.5,0.5。程序运行在MATLAB 2014a平台上,计算机配置为Intel© CoreTM i5-3230M CPU @ 2.6GHz,6144 MB RAM。SGA和MPGA算法的实验参数如表2所示。
每个货区的通道0、通道1、通道2、通道3、通道4、通道5的长度分别为15.5,12.5,9.5,6.5,3.5,0.5。程序运行在MATLAB 2014a平台上,计算机配置为Intel© CoreTM i5-3230M CPU @ 2.6GHz,6144 MB RAM。SGA和MPGA算法的实验参数如表2所示。
表2 算法参数设定
Tab.2 Algorithm parameters setting
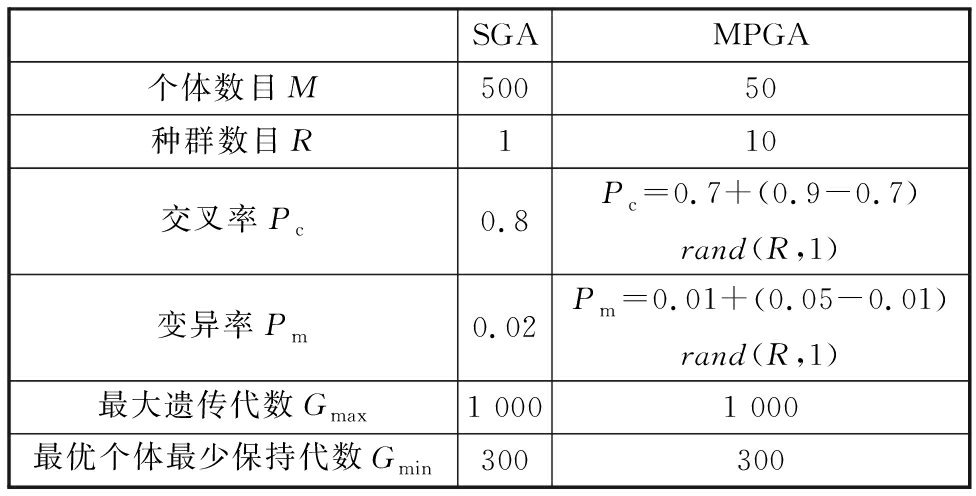
SGAMPGA个体数目M50050种群数目R110交叉率Pc0.8Pc=0.7+(0.9-0.7)rand(R,1)变异率Pm0.02Pm=0.01+(0.05-0.01)rand(R,1)最大遗传代数Gmax1 0001 000最优个体最少保持代数Gmin300300
3.2 实验结果及分析
随机拣选30个物品的订单样本数据,物品位置信息见表3。
表3 订单中30个物品的货位及其编号
Tab.3 Information about the location and the serial number of 30 items in the order
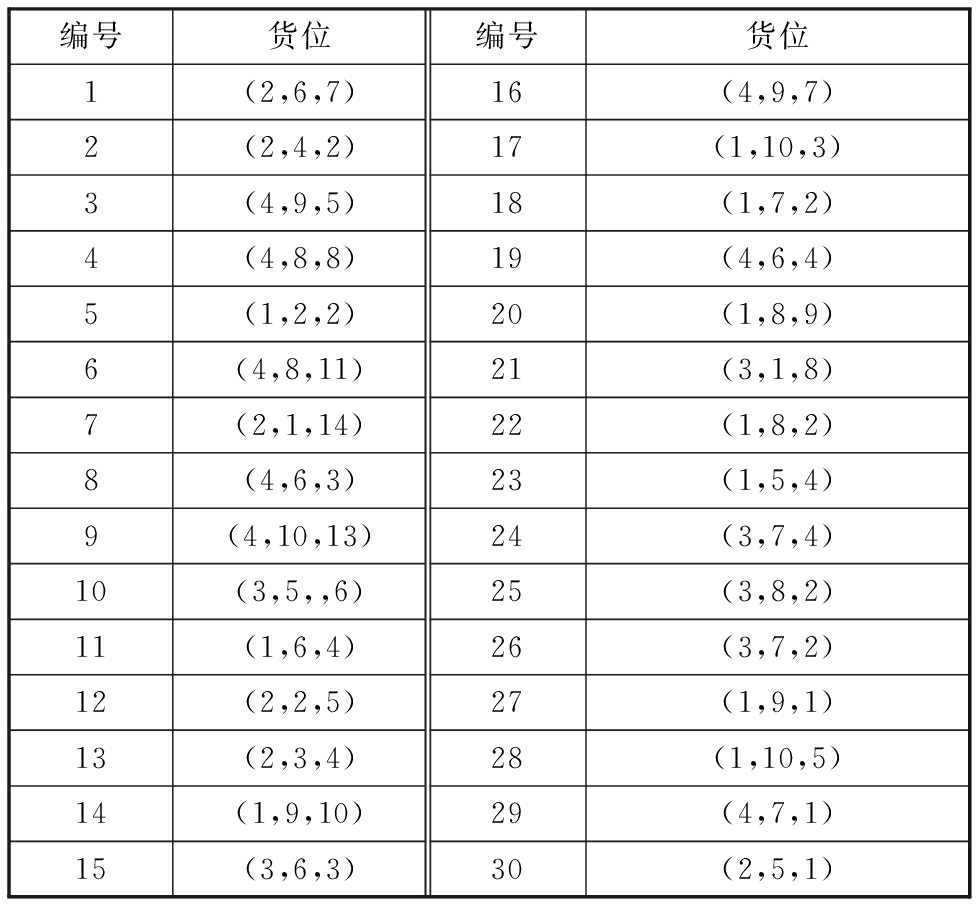
编号货位编号货位1(2,6,7)16(4,9,7)2(2,4,2)17(1,10,3)3(4,9,5)18(1,7,2)4(4,8,8)19(4,6,4)5(1,2,2)20(1,8,9)6(4,8,11)21(3,1,8)7(2,1,14)22(1,8,2)8(4,6,3)23(1,5,4)9(4,10,13)24(3,7,4)10(3,5,,6)25(3,8,2)11(1,6,4)26(3,7,2)12(2,2,5)27(1,9,1)13(2,3,4)28(1,10,5)14(1,9,10)29(4,7,1)15(3,6,3)30(2,5,1)
用S-Shape、SGA和MPGA 3种算法分别进行仿真实验,实验结果见表4。MPGA算法得到的拣选路线图见图9。
表4 S-Shape、SGA和MPGA的结果比较
Tab.4 Comparison of results of S-Shape, SGA and MPGA

方法S-ShapeSGAMPGA总行走距离230.468 0208.455 8200.627 4收敛耗时(s)29.8820.35
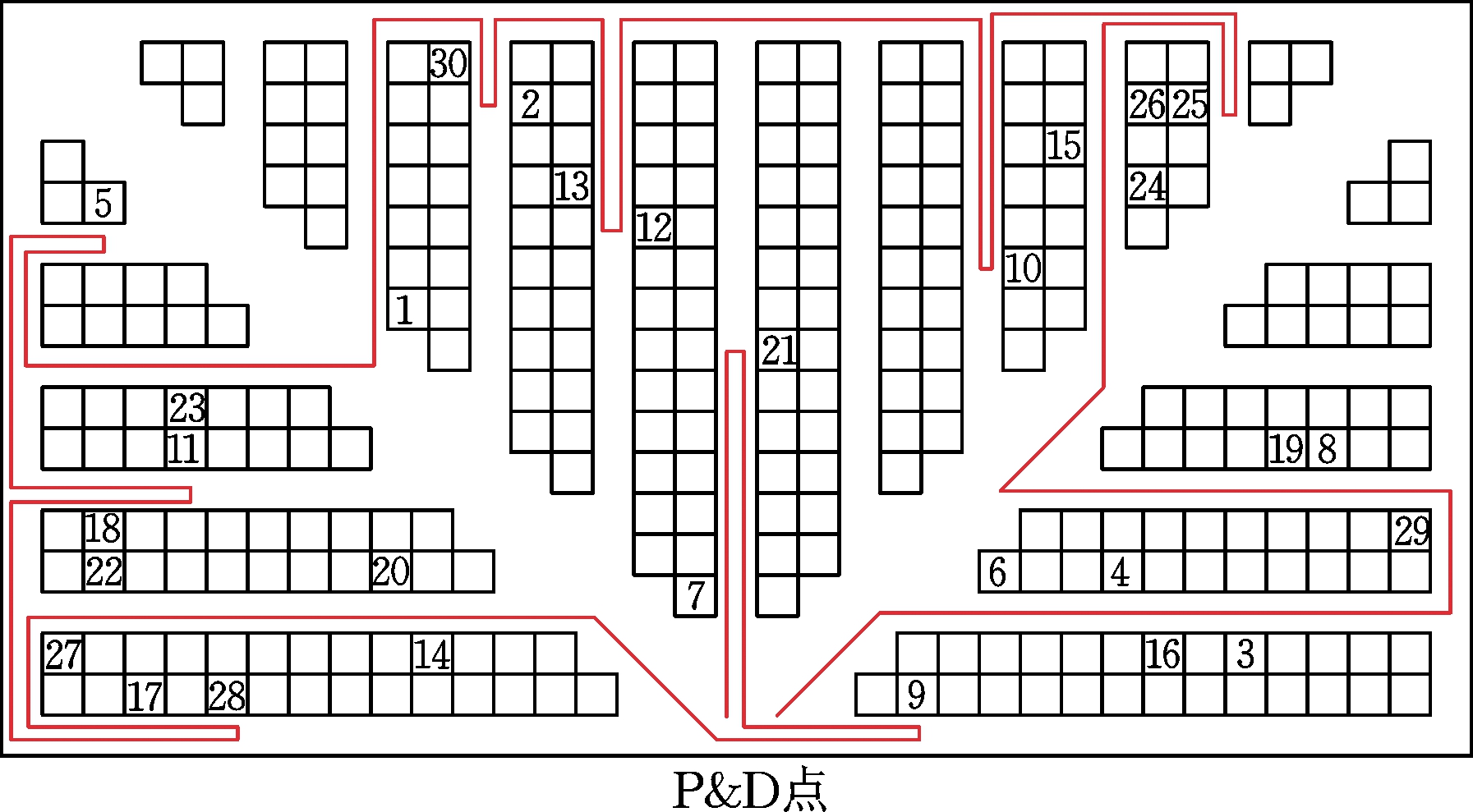
图9 MPGA算法的路径规划图
Fig.9 Route planning diagram of MPGA
为了更全面、准确地评估MPGA的性能,本文将用S-Shape、SGA和MPGA 3种算法对订单规模分别为10、20、30、40、50的情况各重复进行50次实验,每个订单规模下的待拣选货位是随机产生的,3种算法的实验结果如表5所示。
从表5中一系列实验结果可以分析出,不同订单规模下,MPGA算法求解出的平均拣选距离比S-Shape算法大约少9%~16%,其优化程度在小规模订单下更显著;相较于SGA算法,优化比约为0~7%,其优化程度在大规模订单下更显著,而且在收敛耗时上,MPGA也优于SGA,即能更快地找到最优解。
表5 3种算法的实验结果
Tab.5 Experimental results of three algorithms

订单规模平均行走距离及优化比收敛耗时(s)S-ShapeSGAMPGAOpt1(%)Opt2(%)SGAMPGA10130.526 9109.598 0109.598 016.001.501.9920191.254 8167.397 0162.911 714.82.718.3512.5630230.468 0208.455 8200.627 412.93.829.4519.9840238.840 6227.598 0215.799 09.65.251.9032.9650256.225 4248.183 8232.012 29.16.582.5259.61
注:1.S-Shape算法的求解时间可以忽略不计;2.Opt1表示MPGA较S-Shape的距离优化程度,Opt2表示MPGA较SGA的距离优化程度。
4 结语
本文建立了一种鱼骨仓储布局下的路径优化模型,并设计了一种多种群遗传算法(MPGA)来优化该仓储布局下的拣选路径。针对不同订单规模,将MPGA的计算结果与传统遗传算法(SGA)和S-Shape算法的计算结果进行了比较,结果显示MPGA算法能够很好地优化拣选路径,提高作业效率。
[1] KOSTER D R, LE-DUC T, ROODBERGEN K J. Design and Control of Warehouse Order Picking: a Literature Review[J]. European Journal of Operational Research, 2007, 182(2): 481-501.
[2] PETERSEN C G. An Evaluation of Order Picking Routeing Policies[J]. International Journal of Operations & Production Management, 1997, 17(11): 1098-1111.
[3] PARIKHAB P J. A Travel-time Model for a Person-onboard Order Picking System[J]. European Journal of Operational Research, 2010, 200(2): 385-394.
[4] ROODBERGEN K J, VIS I F A. A Model for Warehouse Layout[J]. IIE Transactions, 2006, 38(10): 799-811.
[5] HONG S, JOHNSON A L, PETERS B A. Batch Picking in Narrow-aisle Order Picking Systems with Consideration for Picker Blocking[J]. European Journal of Operational Research, 2012, 221(3): 557-570.
[6] LE-DUC T, KOSTER D R. Travel Time Estimation and Order Batching in a 2-block Warehouse[J]. European Journal of Operational Research, 2007, 176(1): 374-388.
[7] VIGNALI G. Optimisation of Storage Allocation in Order Picking Operations through a Genetic Algorithm[J]. International Journal of Logistics Research & Applications, 2012, 15(2): 127-146.
[8] KOSTER D R, LE-DUC T, ZAERPOUR N. Determining the Number of Zones in a Pick-and-Sort Order Picking System[J]. International Journal of Production Research, 2012, 50(3): 757-771.
[9] KULAK O, TANER M E. Joint Order Batching and Picker Routing in Single and Multiple-cross-aisle Warehouses Using Cluster-based Tabu Search Algorithms[J]. Flexible Services & Manufacturing Journal, 2012, 24(1): 52-80.
[10] BOTTANI E, MONTANARI R, RINALDI M, et al. Intelligent Algorithms for Warehouse Management[J]. Intelligent Systems Reference Library, 2015, 87: 645-667.
[11] CHEN F Y, WANG H W, QI C, et al. An Ant Colony Optimization Routing Algorithm for Two Order Pickers with Congestion Consideration[J]. Computers & Industrial Engineering, 2013, 66(1): 77-85.
[12] PETERSEN C G. The Impact of Routing and Storage Policies on Warehouse Efficiency[J]. International Journal of Operations & Production Management, 1999, 19(10): 1053-1064.
[13] 陈呈频,韩胜军,鲁建厦,等. 多车场与多车型车辆路径问题的多染色体遗传算法[J]. 中国机械工程, 2018, 29(2): 218-223.
CHEN Chengpin, HAN Shengjun, Lu Jiansha, et al. A Multi-chromosome Genetic Algorithm for Multi-depot and Multi-type Vehicle Routing Problems[J]. China Mechanical Engineering, 2018, 29(2): 218-223.
[14] 高海昌,冯博琴,朱利. 智能优化算法求解TSP问题[J]. 控制与决策, 2006, 21(3): 241-247.
GAO Haichang, FENG Boqin, ZHU Li. Reviews of the Meta-heuristic Algorithms for TSP[J]. Control and Decision, 2006, 21(3): 241-247.
[15] 王宏,符卓,左武. 基于遗传算法的双区型仓库拣货路径优化研究[J]. 计算机工程与应用, 2009, 45(6): 224-228.
WANG Hong, FU Zhuo, ZUO Wu. Genetic Algorithm for Picking Routing Problem in 2-block Warehouse[J]. Computer Engineering and Applications, 2009, 45(6): 224-228.
[16] 陈方宇,王红卫,祁超,等. 考虑多拣货员堵塞的仓库拣选路径算法[J]. 系统工程学报, 2013(5): 581-591.
CHEN Fangyu, WANG Hongwei, QI Chao, et al.Routing Method for Multiple Order Pickers with Congestion Consideration[J]. Journal of Systems Engineering, 2013(5): 581-591.
[17] GUE K R, MELLER R D. Aisle Configurations for Unit-load Warehouses[J]. IIE Transaction, 2009(3): 171-182.
[18] ROODBERGEN K J, KOSTER D R. Routing Methods for Warehouses with Multiple Cross Aisles[J]. International Journal of Production Research, 2001, 39(9): 1865-1883.
[19] HALL R. Distance Approximations for Routing Manual Pickers in a Warehouse[J]. IIE Transactions, 1993, 25(4): 76-87.
[20] SHARP G P. Designing the Layout Structure of Manual Order Picking Areas in Warehouses[J]. IIE Transactions, 2008, 40(11): 1032-1045.
[21] PETERSEN C G, AASE G. A Comparison of Picking, Storage, and Routing Policies in Manual Order Picking[J]. International Journal of Production Economics, 2005, 92(1): 11-19.
[22] XIAO J, ZHENG L. A Correlated Storage Location Assignment Problem in a Single-block-multi-aisles Warehouse Considering BOM Information[J]. International Journal of Production Research, 2010, 48(5): 1321-1338.
[23] POHL L M, MELLER R D, GUE K R. Optimizing Fishbone Aisles for Dual-command Operations in a Warehouse[J]. Naval Research Logistics, 2009, 56(5): 389-403.
[24] 雷英杰,张善文. MATLAB遗传算法工具箱及应用[M]. 西安:西安电子科技大学出版社, 2014: 1-10.
LEI Yingjie, ZHANG Shanwen. MATLAB Genetic Algorithm Toolbox and Application[M]. Xi’an: Xidian University Press, 2014: 1-10.
[25] LIU Y,SONG J,WEN J Y. An Optimizing Algorithm of Static Task Scheduling Problem Based on Bybrid Genetic Algorithm[J]. High Technology Letters, 2016, 22(2): 170-176.
[26] 林阳,赵欢,丁汉. 基于多种群遗传算法的一般机器人逆运动学求解[J]. 机械工程学报, 2017,53(3): 1-8.
LIN Yang, ZHAO Huan, DING Han. Solution of Inverse Kinematics for General Robot Manipulators Based on Multiple Population Genetic Algorithm[J]. Journal of Mechanical Engineering, 2017,53(3): 1-8.
