0 引言
传统的刚性机械手刚度大、操作精度高,但也存在质量大、惯性力大、不易折叠等缺点,难以在狭小空间内完成柔顺性要求较高的精密操作;柔性机械手尽管具有极强的可调性和柔顺性,且质量小,但其柔性单元在运动过程中易出现弯曲、扭转与剪切等变形,力学建模与控制较为困难[1]。因此,设计并优选兼顾二者优点的刚柔构件混合机构具有重要的研究意义和应用价值。
张拉整体结构是由非连续的受压构件和连续的柔性构件组成的自应力平衡系统[2],具有可折叠、质量小、惯性力小等特点[3-4],在雕塑、建筑等领域得到了广泛应用。受张拉整体结构构型方法的启发,近年来,国内外学者通过将受压的刚性构件用伸缩杆驱动,将受拉的柔性构件用弹簧或绳索驱动,提出了一种刚柔混合的新型机构,即张拉整体机构。弹簧或绳索的应用使得这类机构的质量及惯性力得到了显著减小,且内部所有构件均承受纯轴向力,结构强度得到了提高;此外,这种机构具有良好的柔顺性和可折叠性能,在空天折叠系统[2]、能量收集装置[5]、精密操作机器人[6]等领域具有广泛的应用前景。
传统刚性机构的构型综合方法较多,如螺旋理论、位移子群、方位特征理论等,均各自形成了比较完整的理论体系,为机构的创新设计提供了坚实的理论基础。而对于张拉整体机构,拓扑结构综合的系统理论尚未形成,目前的机构构型大多来自于张拉整体结构的联想和推理。平面张拉整体机构的结构较为简单,BAYAT等[7]率先提出了一种二弹簧平面张拉整体机构,VASQUEZ等[5]、ARSENAULT等[8]、SHAI等[9]在此基础上均提出了类似结构的演化机构,而CHEN等[10] 、JI 等[11]则设计了由基本单元叠加的二级平面张拉整体机构。空间张拉整体机构构型比较单一,大多是基于三杆九索[12-15]或四杆十二索[16-17]张拉整体结构的设想得到,运动特征类似于Stewart并联机构,均为全自由度运动输出。
柔性元件的应用使得张拉整体机构分析起来变得更加复杂。目前国内外文献大多集中于运动学问题[11-14],既要考虑张拉整体机构运动输入和输出变量之间的关系,又要考虑机构工作空间内的静态平衡,通用的做法是求解最小能量约束下的位置正反解。传统刚性机构的位置正解可通过结构降耦[18]或运动弱耦合设计[19]的方式求得方程表达式,但张拉整体机构的正解难以通过类似的方法得到,只能求解数值解。对于动力学分析,目前相关研究报道较少,如ARSENAULT等[8]全面分析了一种平面张拉整体机构的动力学;ABADI等[12-13]对空间三杆张拉整体机构的动力学进行了模型仿真,但未对动力学方程进行数值验证;朱伟等[16]建立了四杆张拉整体机构的动力学模型,并进行了仿真验证。总之,这方面的工作还需要进一步深入研究。
本文根据Assur组的机构组成基本原理,提出了一类平面张拉整体机构的拓扑结构综合方法,并设计了一种可用于精密操作的新型平面张拉整体并联机构。该机构由2根柔性构件(弹簧或绳索)和4根刚性构件组成,包括2个刚性驱动支链和1个柔性驱动支链,具有三自由度运动输出。该机构中弹性元件的应用明显减小了机械手的质量和运动惯性力,操作时减少了机械手和被抓取对象之间的刚性冲击。当机构处于平衡位置时,受弹簧最小势能的约束,机构始终保持平衡状态。本文分析了机构的位置正反解、奇异位形及工作空间等运动学问题,研究了机构的刚度及平衡状态下的机构刚度分布特性,最后对机构动力学模型进行了分析与验证。
1 机构设计
1.1 机构来源
Assur杆组是机构的基本组成单元,图1a所示为连接到机架的Ⅲ级Assur杆组,其中所有节点均为转动副(R副)连接。根据文献[9],当在任意关节点上施加外力时,杆组的所有杆都会产生受力;反之,若部分杆件不受力,则不是Assur杆组。如图1b所示,在关节点D处施加外力时,杆DE和EC不受力,故它不属于Assur杆组。

(a)Assur杆组 (b)非Assur杆组
图1 Assur杆组与非Assur杆组
Fig.1 Assur rod group and non-Assur rod group
文献[20]在数学上证明了Assur杆组存在某种特殊组合和几何性质,即杆组中所有杆件具有唯一的静态自应力特征。在图1a中,Ⅲ级Assur杆组中3个杆件AD、BE、CF的延长线交于O点,该点即为杆组的绝对瞬心,此时杆组处于平衡位置,所有杆件静态平衡。
张拉整体结构是由刚性构件和柔性构件组成的自应力结构体,刚性构件只承受压力,柔性构件只承受拉力,整个结构处在一种拉压平衡的状态中,是一种自由度为零的自应力平衡体系,这一点与Assur杆组十分类似。由此,通过改变Assur杆组中部分杆件属性,并使之保持自平衡条件,即可得到部分张拉整体机构构型。具体方法如下:
(1)选取Assur杆组结构形式,去除Assur杆组中1个或多个刚性杆,用柔性绳索或弹簧替代,判断杆组是否满足自平衡条件;
(2)在杆组连接节点处增加相应的单自由度运动副,根据机构实际需要,在杆组中增加驱动副或驱动杆,初步得到张拉整体机构;
(3)判断机构是否具有确定的运动输出,并确定机构的自由度,判断机构的运动性能与拓扑性能,最终得到张拉整体机构。
图1a中的Ⅲ级Assur杆组可演化成图2所示的几种Ⅲ级平面张拉整体机构。图2中,粗线表示刚性杆,细线表示弹性绳索或弹簧。为始终保证机构中柔性构件连续受拉、刚性构件受压的状态,通常采用绳驱动方式(图2a),或是采用刚性杆和绳索联合驱动方式(图2b~图2f)。图2g~图2i中两侧为柔性构件,其中左侧柔性构件为弹簧,右侧为驱动绳索,驱动绳索可等效为绳索和弹簧的组合,通过调节驱动绳索与其他构件间的几何位置关系来保持机构始终张拉平衡,当弹性构件势能处于极值点时,机构可保持平衡。
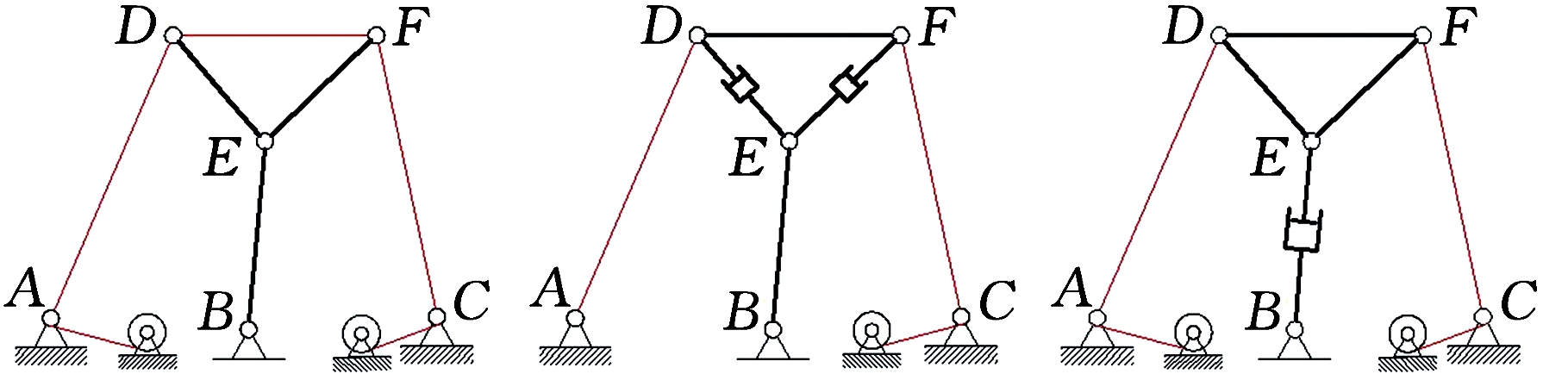
(a) (b) (c)

(d) (e) (f)

(g) (h) (i)
图2 Ⅲ级平面张拉整体机构
Fig.2 Ⅲ-class planar tensegrity mechanisms
1.2 机构描述
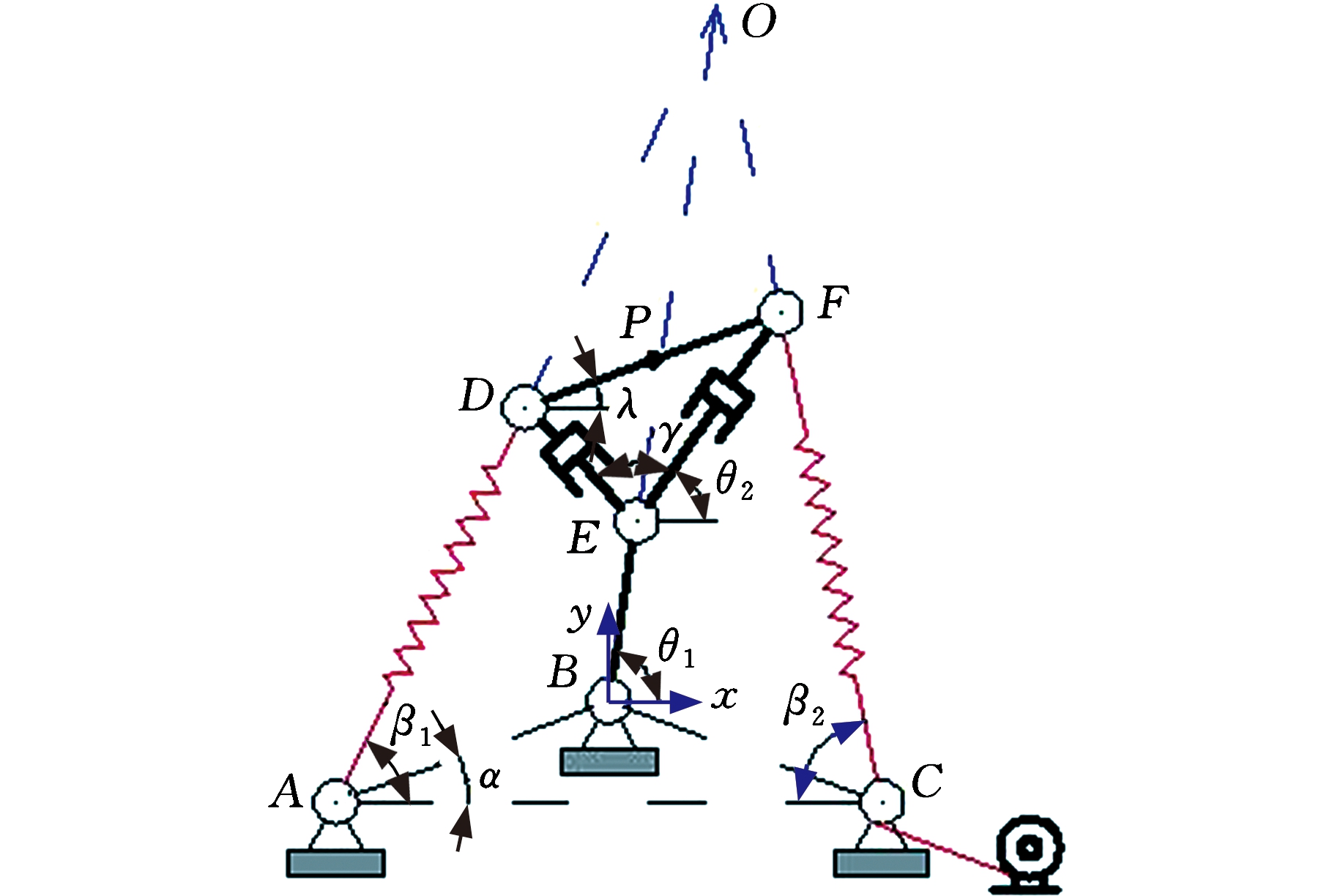
图3 机构简图
Fig.3 Schematic diagram of mechanism
根据上述Assur杆组的性质及平面张拉整体机构的组成原理,以图2g模型为例来研究这类张拉整体机构的运动学、刚度以及动力学特征。机构平面简图见图3,该机构由弹性构件AD和CF、定长杆BE和DF以及伸缩驱动杆DE和EF组成。点A、B、C处通过转动副连接于基座上,各构件的连接点D、E、F处均采用转动副连接。驱动绳索CF与卷轴电机相连,通过改变绳索的长度来确保机构处于张紧平衡状态,如图3所示。根据机构静态自应力特征,3个构件AD、BE、CF必交于O点,O点即为该机构的绝对瞬心[20]。
平面张拉整体机构的运动自由度计算方法与平面机构类似,需要注意的是驱动绳索CF可看作由绳索和弹簧串联而成,可等效成2个构件和1个移动副。图3中,活动构件数nl=9,低副数Pl=12(包括9个转动副和3个移动副),则机构的自由度为
FDOF=3nl-2Pl=3×9-2×12=3
可见,该机构自由度为3,可实现平面内一转动两移动的运动输出。
2 运动学分析
建立图3所示的坐标系Bxy,其中B为原点,x轴平行于AC向右,以垂直于x轴向上的方向为y轴的正方向。设杆BE与x轴正方向的夹角为θ1,杆DF与x轴正方向的夹角为λ,杆EF与x轴正方向的夹角为θ2,杆DE、EF的夹角为γ,可伸缩杆DE、EF的长度分别为L1、L2,定长杆BE、DF的长度分别为L、c。
设AB=BC=a,AC=b。在图3中,弹簧受到的力由刚度系数Ki及其自身长度li(i=1,2)共同决定,其重力可忽略不计。机构中将L1、L2作为输入变量,将动平台质心P点作为机构的输出变量,其坐标为P(x,y),而动平台的姿态可用θ1、θ2、λ来描述,角度θ1、θ2和λ的取值范围分别为:0°≤θ1≤180°,-90°≤θ2≤180°,-90°≤λ≤180°。
与传统机构不同,张拉整体机构的输入和输出变量之间的关系依赖于内力,需要同时考虑该机构的运动学和静力学特性。由于在张拉整体机构中的输入和输出变量之间的关系由机构的几何形状和弹簧所受的拉力共同决定,在对机构进行运动学和静力学分析时,通常假设机构处于平衡状态,因此,需在输入和输出变量之间建立明确的关系。
2.1 运动学位置反解
机构的位置反解是,已知动平台质心P点的位姿(x,y,λ),求解机构的输入变量L1和L2。根据图3中的位置关系,点A、B、C、D、E、F的坐标向量可分别表示为
A=(-acos α,-asin α) B=(0,0)
C=(acos α,-asin α)![]()
E=(Lcos θ1,Lsin θ1)![]()
当机构处于平衡状态时,由Assur杆组的性质可知,弹性构件AD、CF和杆BE的延长线交于O点,该点即为该机构的绝对瞬心。由图3所示的位置关系可得到机构在平面直角坐标系中的矢量关系方程:
mRAD+RBA=nRCF+RBC=pRBE
(1)
其中,RBA、RBC、RBE分别为沿直线BA、BC、BE方向的方向矢量,可由点A、C、E的坐标向量得到;m、n、p分别为方向矢量RAD、RCF、RBE的系数;RAD、RCF分别为沿直线AD、CF方向的方向矢量,可表示为

将RAD、RCF的表达式代入式(1),解得


式中,xB、xC分别为B点、C点的横坐标;yB为B点的纵坐标。
整理式(1)~式(3),可得机构的位置反解方程式:
L1=
(4)
L2=
(5)
2.2 运动学位置正解
机构的运动学正解是,利用给定机构的输入变量L1、L2求解出机构动平台质心P点的输出变量x、y和λ。对于该张拉整体机构,由给定的杆DE、EF的长度来计算出P点的坐标,机构位姿可用θ1、θ2、λ来描述。由图3中的坐标系可求得点D、E、F的坐标向量分别为
D=(Lcos θ1+L1cos(θ2+γ),Lsin θ1+L1sin(θ2+γ))
E=(Lcos θ1,Lsin θ1)
F=(Lcos θ1+L1cos(θ2+γ)+ccos λ,Lsin θ1+
L1sin(θ2+γ)+csin λ)
图3中,设杆DE和杆DF的夹角为φ,杆DE与x轴正方向的夹角为φ,根据图示关系可得
φ=θ2+γ=π-λ+φ
(6)
根据图3中的几何关系可求得P点的横纵坐标,分别为
![]()
根据最小势能法原理,当且仅当机构总的势能U处于极值点时,机构处于平衡状态。忽略机构的重力势能,只考虑机构的弹性势能Ep,则机构总的势能可表示为
![]()
2cL1cos φ-4LL1cos(θ1-λ+φ)+
4aL1sin(-λ+φ)sin α+2cLcos(θ1-λ)+
4aLsin θ1sin α)
(9)
式中,Ki为弹簧的刚度系数,K1=K2=k。
在式(9)等号两边分别对θ1和λ进行求导,可得
![]() =k(2L1Lsin(θ1-λ+φ)+
=k(2L1Lsin(θ1-λ+φ)+
2aLsin αcos θ1-cLsin(θ1-λ))
(10)
![]() =k(-2L1Lsin(θ1-λ+φ)+acsin(λ+α)-
=k(-2L1Lsin(θ1-λ+φ)+acsin(λ+α)-
2aL1sin αcos(-λ+φ)+cLsin(θ1-λ))
(11)
根据最小势能法的约束条件,令![]() 0,并代入式(10)、式(11)可得
0,并代入式(10)、式(11)可得
S=8acLsin α-16aL1sin αcos φ
将式(6)、式(12)、式(13)代入式(7)、式(8),即可求得输出点P的坐标。
2.3 算例验证
设计机构的具体几何参数如下:a=320 mm,b=600 mm,c=300 mm,L=200 mm。
当输入参数L1、L2已知时,根据P点的坐标表达式可求得机构的位置正解数值解,如表1所示。将表1中的输出参数代入反解方程(式(4)、式(5)),可得到位置反解,如表2所示。由表1、表2可知,位置正反解计算的数值基本吻合,也验证了绝对瞬心法求位置反解与最小势能法求位置正解的结果是一致的。表1中计算得到的两组正解所对应的机构位姿图见图4,其中图4a~图4c为第一组正解的位姿图,图4d~图4f为第二组正解的位姿图。将6个位姿图中的弹性构件AD、CF和杆件BE延长,可以发现延长线均交于同一点O,这与图3中的瞬心点基本一致。
表1 位置正解
Tab.1 Positive solutions of the position

序号输入参数输出参数L1(mm)L2(mm)λ(°)x(mm)y(mm)1300.00300.00-32.20211.31406.70300.00300.0000459.80300.00300.0030.00-204.44410.302290.00285.00-57.20420.31156.70290.00285.00-22.30152.40417.43290.00285.0070.08380.50217.57
表2 位置反解
Tab.2 Inverse solutions of the position
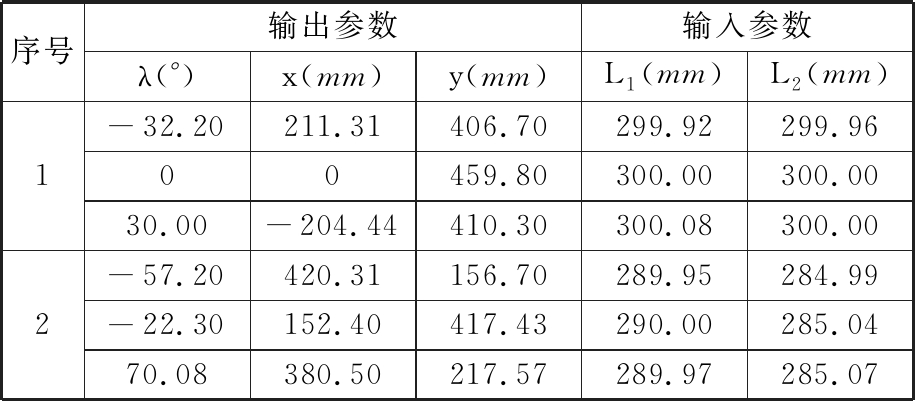
序号输出参数输入参数λ(°)x(mm)y(mm)L1(mm)L2(mm)1-32.20211.31406.70299.92299.9600459.80300.00300.0030.00-204.44410.30300.08300.002-57.20420.31156.70289.95284.99-22.30152.40417.43290.00285.0470.08380.50217.57289.97285.07
3 张拉整体机构运动性能分析
3.1 雅可比矩阵
在机构学中,通常用雅可比矩阵J来描述输入速度和输出速度之间的映射关系。对于所设计的张拉整体机构,设输出速度矩阵为![]() 输入速度矩阵为
输入速度矩阵为![]() 当机构处于平衡状态时,其关系式可表达为
当机构处于平衡状态时,其关系式可表达为
υ=Jζ
(14)

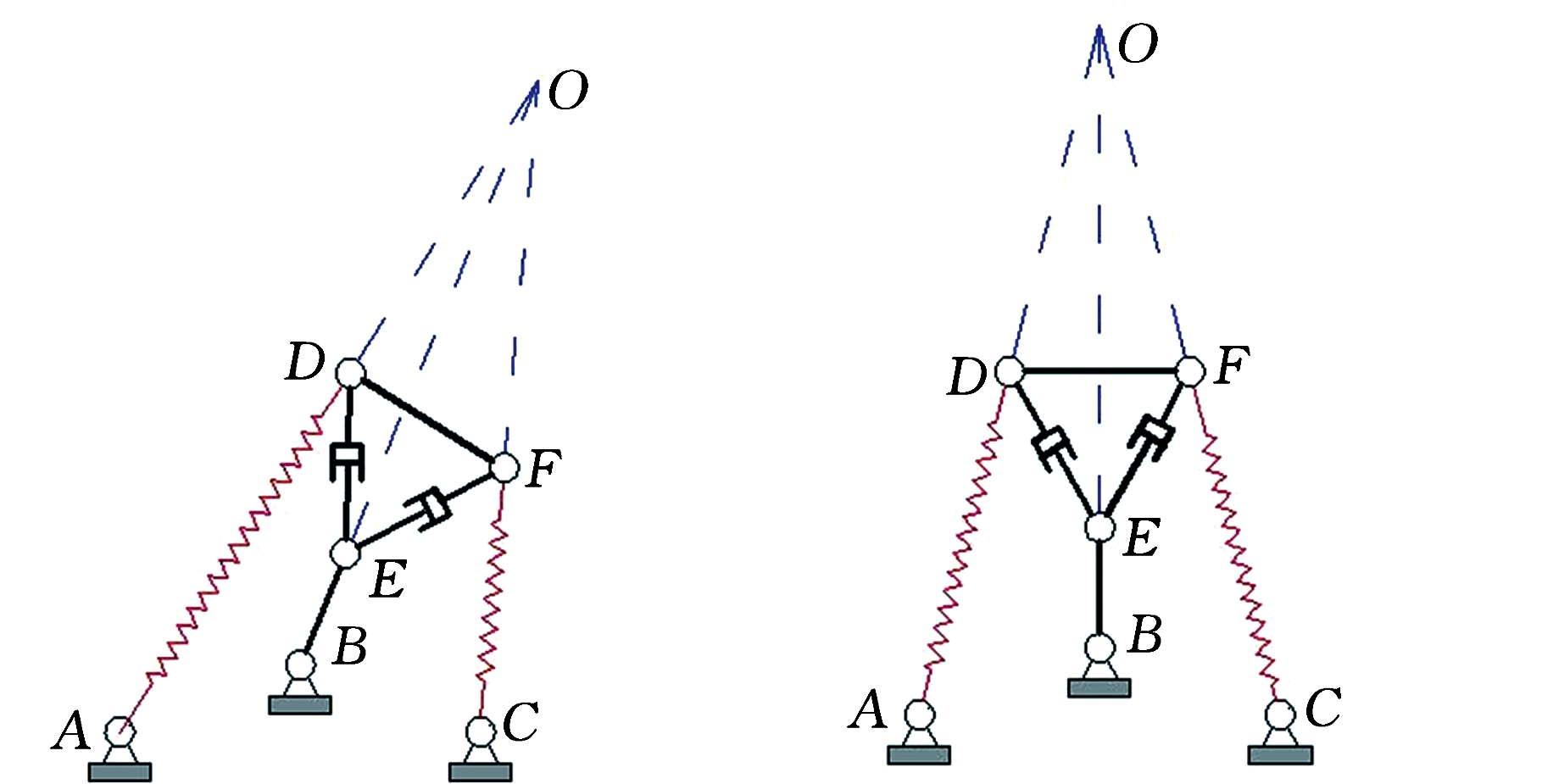
(a)第一组正解位姿图一 (b)第一组正解位姿图二
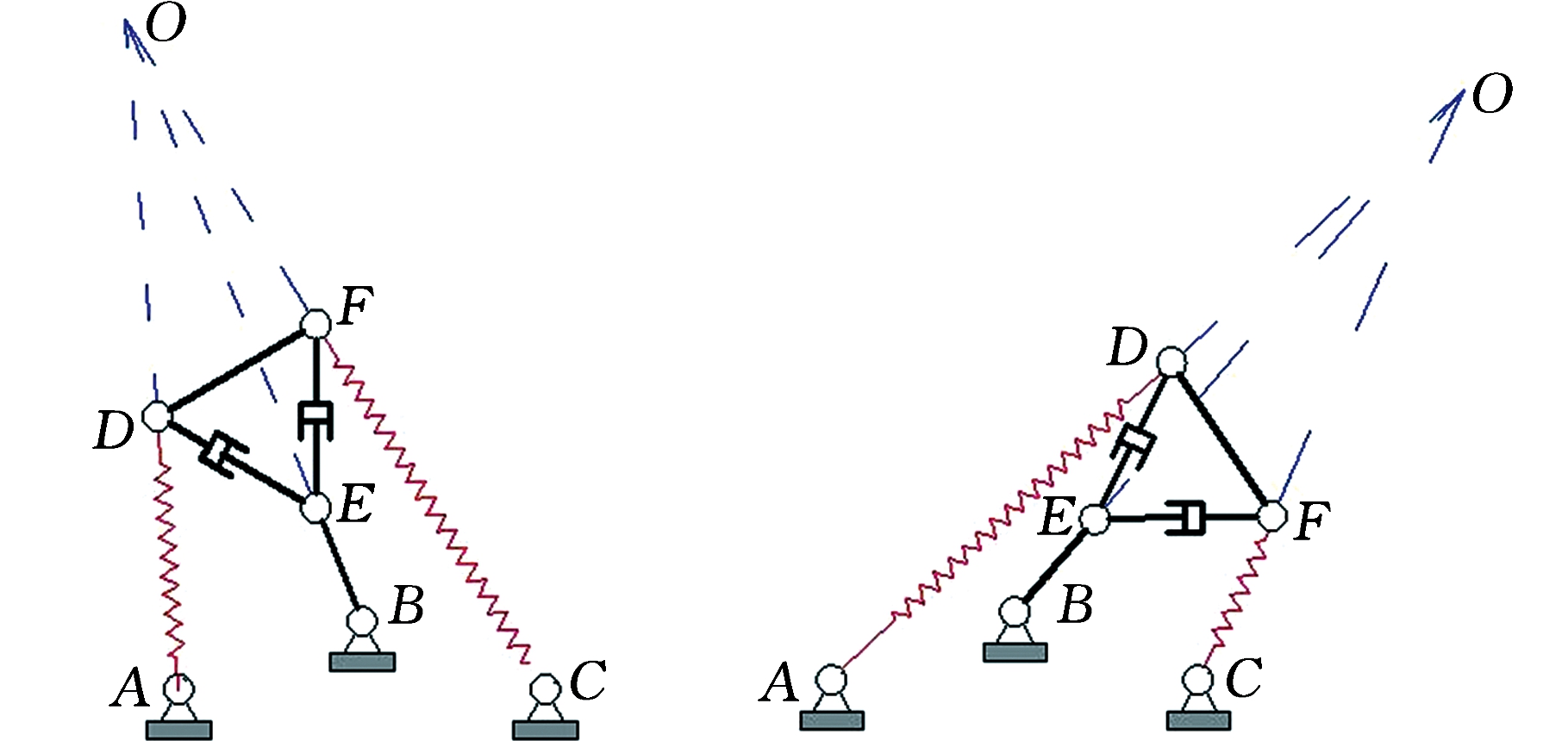
(c)第一组正解位姿图三 (d)第二组正解位姿图一
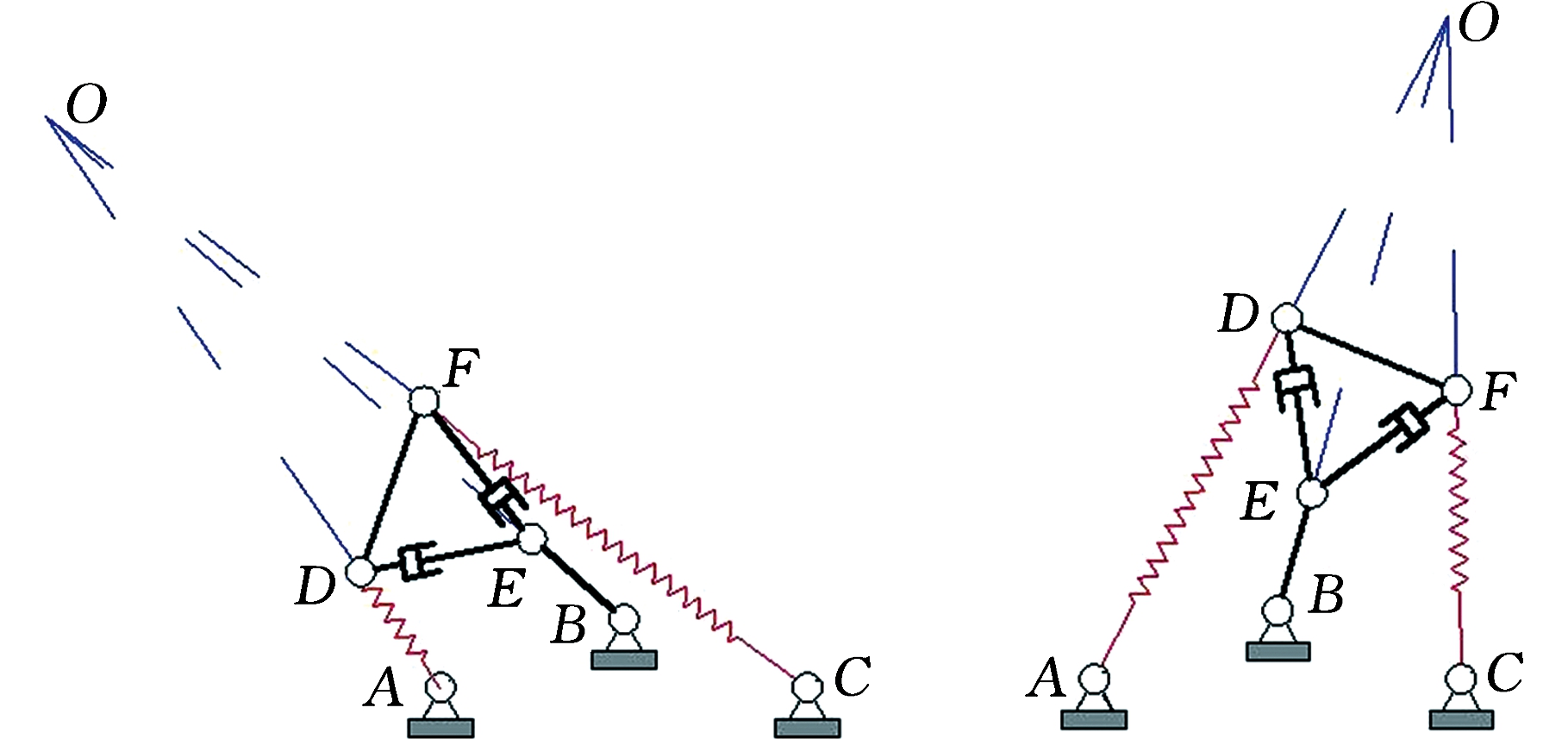
(e)第二组正解位姿图二 (f)第二组正解位姿图三
图4 机构运动位姿
Fig.4 Motion posture of mechanism
根据雅可比矩阵行列式|J|的数值求解情况,可得到机构的奇异位形。
3.2 奇异位形
当雅可比矩阵的行列式|J|等于零或趋于无穷时,机构会发生奇异。
(1)当L1=0时,点D与点E重合,且杆EF与杆DF重合,如图5a所示,此时机构会发生奇异,机构不能保持平衡状态。
(2)当L2=0时,点E与点F重合,且杆DE与杆DF重合,如图5b所示,此时机构会发生奇异,机构不能保持平衡状态。
(3)当![]() 即L1=L2-c或L2=L1-c)时,杆DE、EF、BF共线,如图5c、图5d所示,此时机构会发生奇异,机构不能保持平衡状态。
即L1=L2-c或L2=L1-c)时,杆DE、EF、BF共线,如图5c、图5d所示,此时机构会发生奇异,机构不能保持平衡状态。
(4)当c=L1+L2时,如图5e所示,此时机构会发生奇异,该种奇异是一个特殊位形。
(5)当L=L1cos γ(即![]() )时,如图5f所示,机构处于奇异状态,该种奇异也是一个特殊位形。
)时,如图5f所示,机构处于奇异状态,该种奇异也是一个特殊位形。
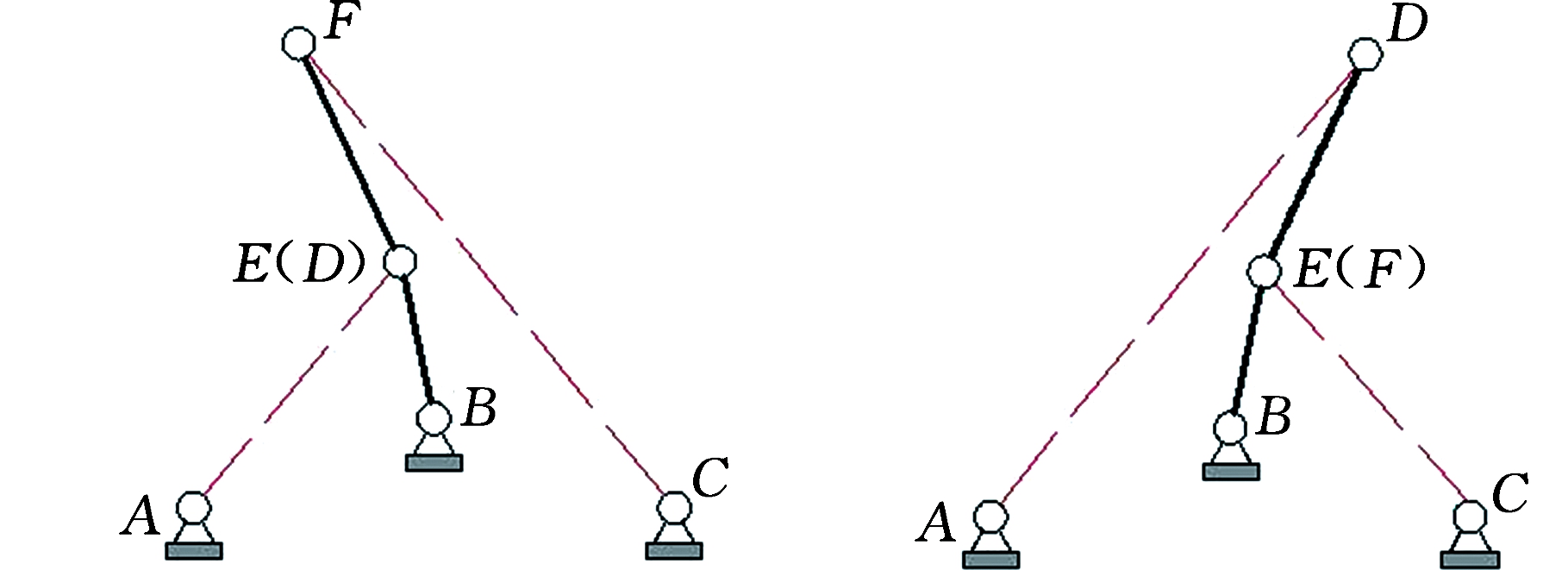
(a)L1=0奇异 (b)L2=0奇异
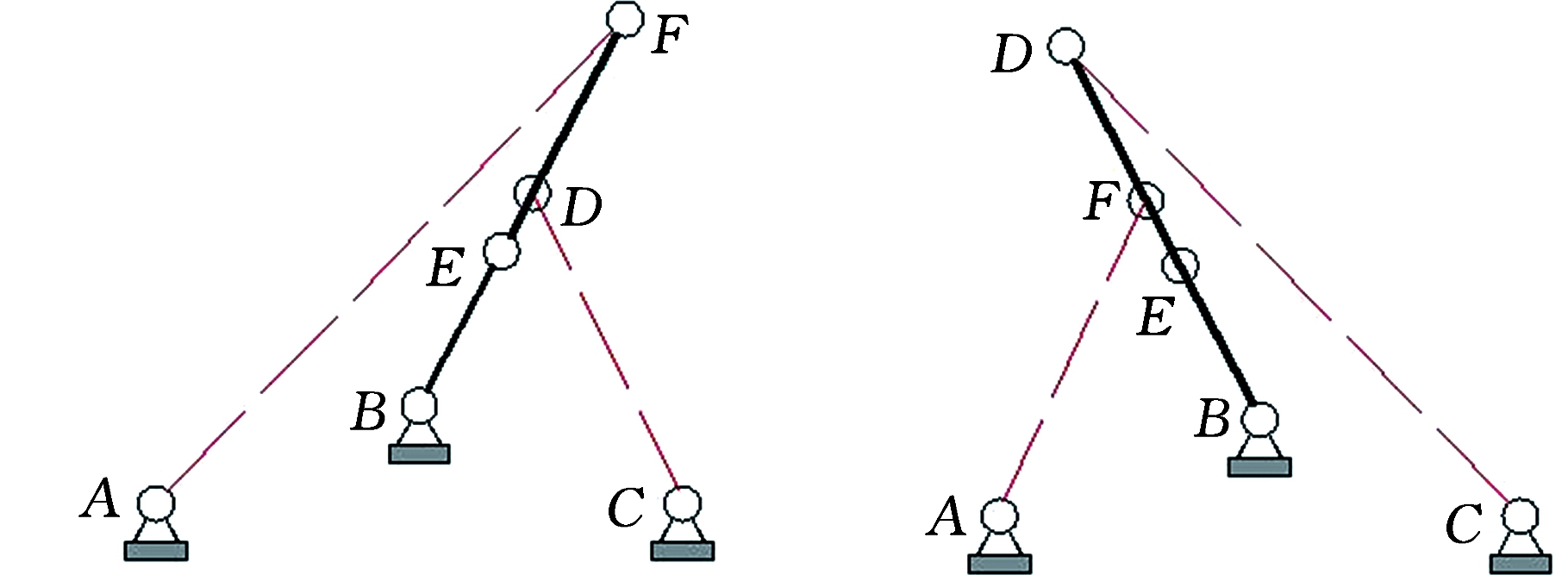
(c)L1=L2-c奇异 (d)L2=L1-c奇异
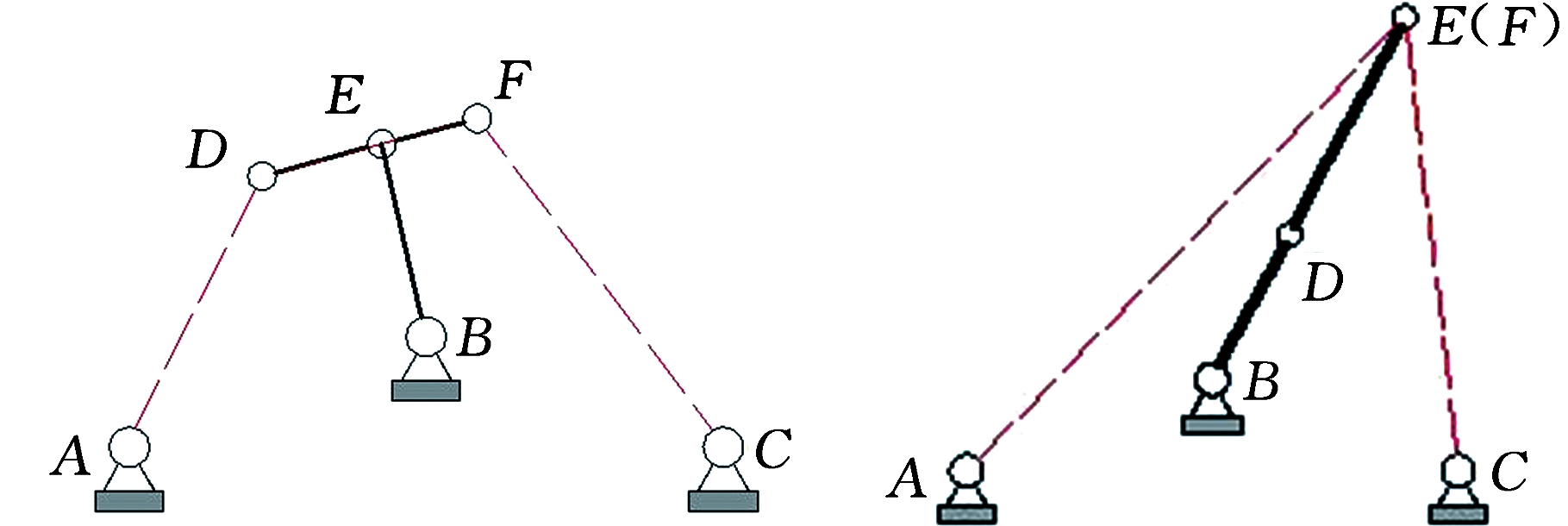
(e)c=L2+L1奇异 (f)L1=cos γ奇异
图5 机构奇异位形
Fig.5 Singular configurations of the mechanism
3.3 工作空间
工作空间的大小是衡量机构运动学性能的重要指标,工作空间的边界通常对应于机构的奇异位置,因此,奇异曲线所围成的区域即为机构的可达工作空间[11]。
3.3.1 驱动工作空间
由机构的奇异位形分析可知,机构的4种奇异位置方程可以视为关于变量L1、L2的函数,同时图3中的三角形DEF必须满足L2>L1-c、L2<L1+c,并给定驱动的最大行程为650 mm,则机构驱动工作空间曲线的方程式如下:

如式(15)所示,每一条曲线均是驱动工作空间的边界,函数Ⅰ、Ⅱ、Ⅲ和Ⅳ对应的线条为机构的4种边界奇异曲线,其中Ⅳ为驱动奇异,而函数Ⅴ为位形奇异曲线,在实际应用时应避免运动到位形奇异曲线上。依据给定的机构参数、机构奇异位形、驱动行程范围,可通过MATLAB绘制出驱动工作空间的曲线,见图6。
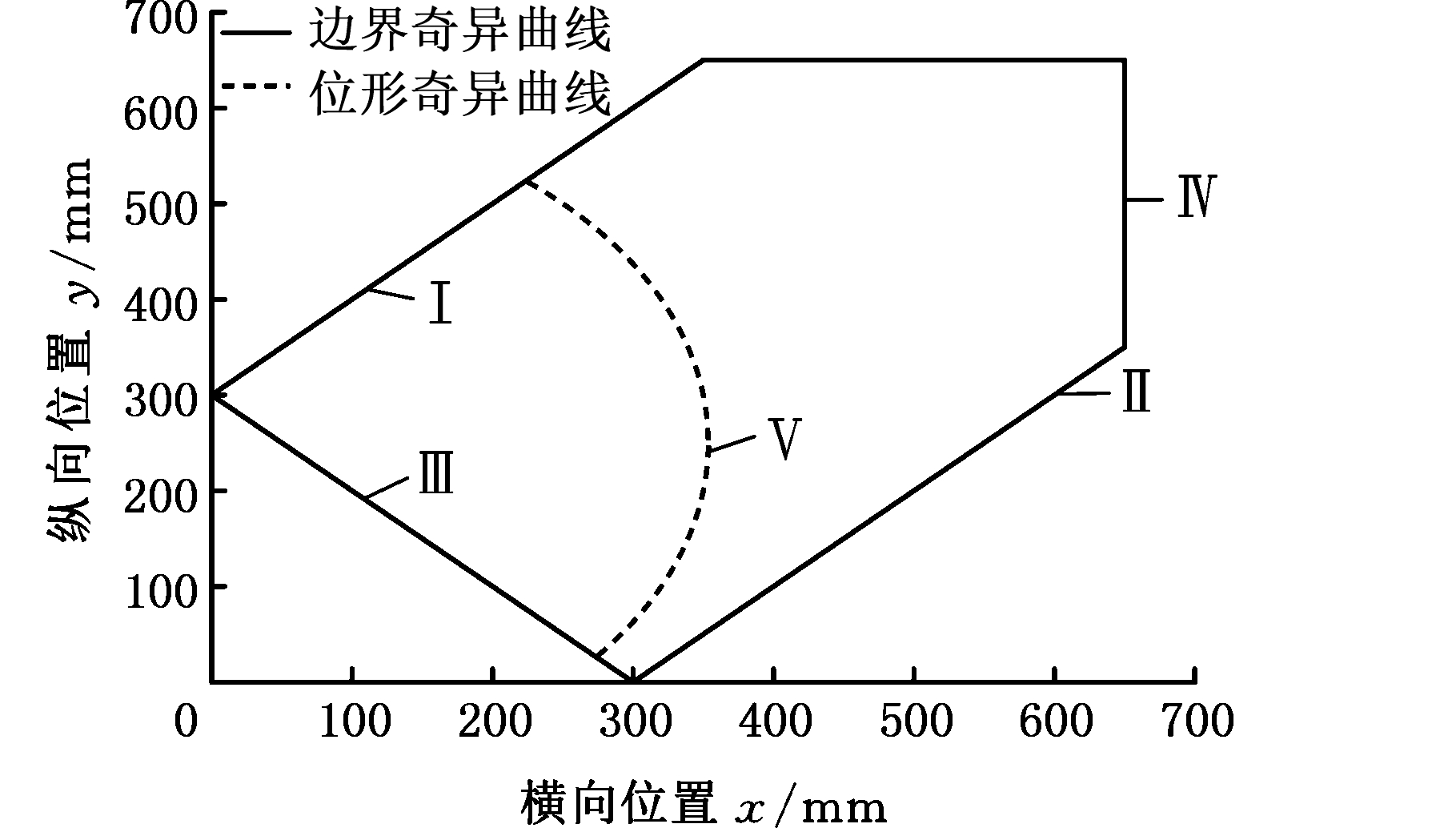
图6 驱动工作空间
Fig.6 Drive workspace
3.3.2 输出工作空间
机构的输出工作空间为末端执行器可达到的区域,输出工作空间的边界对应输出奇异位置曲线的函数。式(15)中的L1、L2可由式(4)和式(5)用x、y、λ表示。再结合给定的机构参数,可得输出工作空间如图7所示。
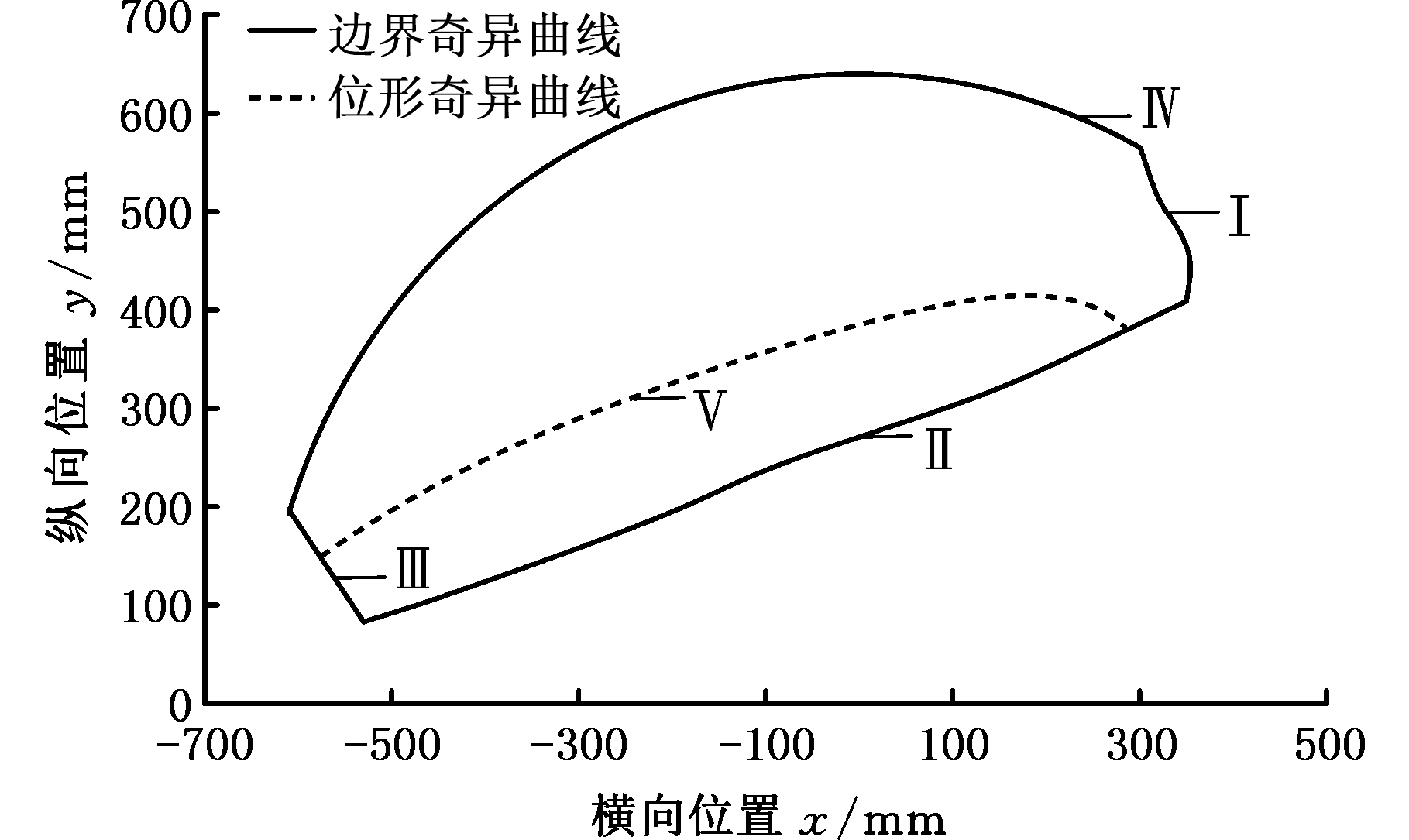
图7 输出工作空间
Fig.7 Export workspace
4 刚度分析
该张拉整体机构中存在两条柔性支链,当机构受到外载作用时,即使机构被锁定也会发生变形,将机构抵抗外部载荷引起变形的能力称为刚度,故需要对机构的刚度性能进行分析。
4.1 刚度模型
如图3所示,当机构的驱动被锁定时,即当输入参数为L1=L2=300 mm时,存在绕点D和绕点B的转动。根据式(9)分别对转动角θ1、λ求导,可以分别求出施加在机构上的外载转矩τθ1、τλ与机构对应变形量∂θ1、∂λ之间的关系,其表达式分别如下:
![]()
2aLcos θ1sin α-cLsin(θ1-λ))
(16)
![]()
cLsin(θ1-λ)-2aL1cos(φ-λ)sin α)
(17)
通过将转矩τθ1、τλ分别对两个转动角θ1、λ对应求导,可得到机构相对于转动角θ1、λ的转动刚度,其表达式分别如下:
![]()
2aLsin θ1sin α-cLcos(θ1-λ))
(18)
![]()
cLcos(θ1-λ)-2aL1sin(φ-λ)sin α)
(19)
机构几何参数的设置与前文相同,根据式(18)、式(19)可绘制出刚度Kθ1、Kλ的分布图,见图8。
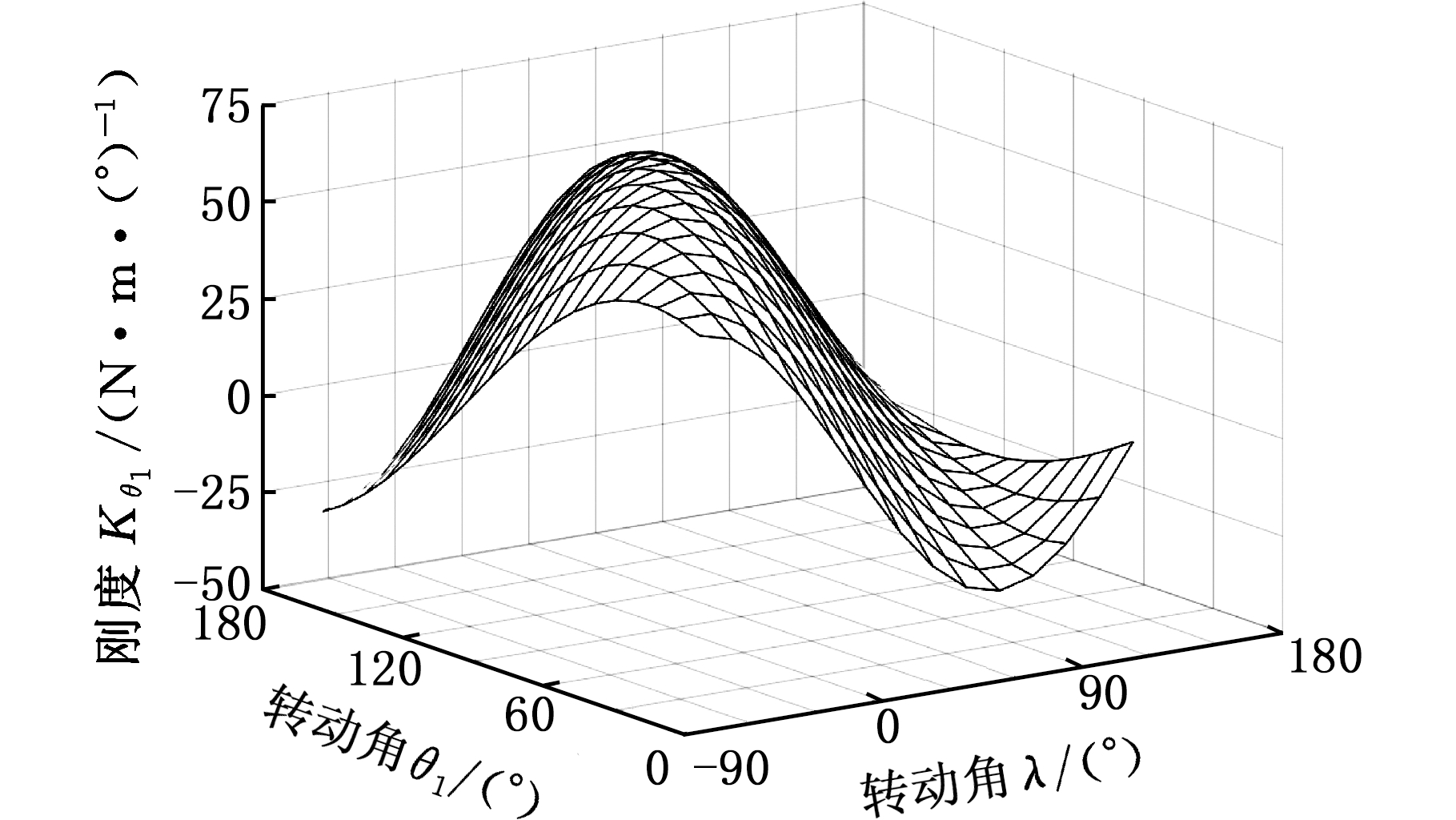
(a)刚度Kθ1
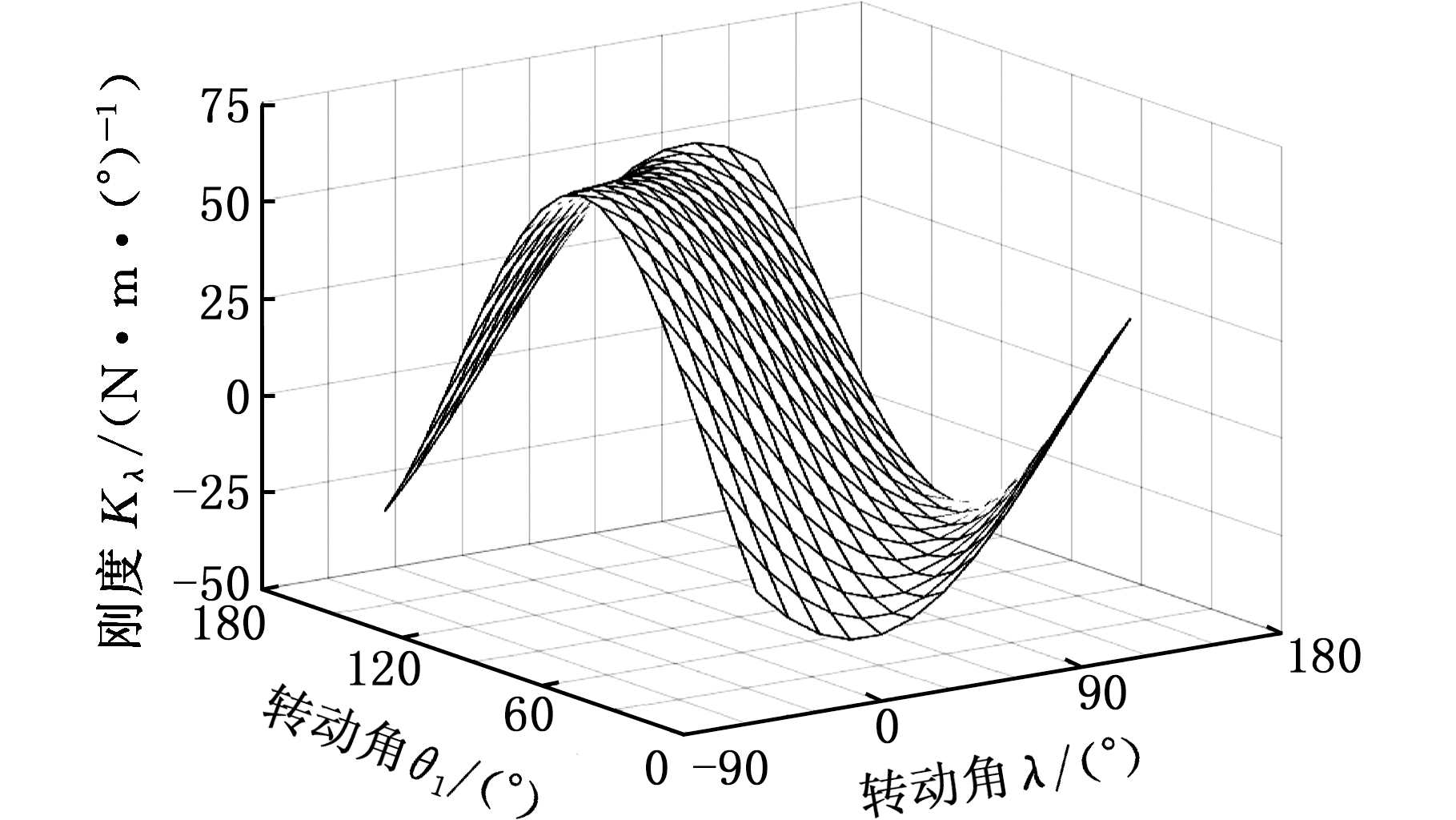
(b)刚度Kλ
图8 张拉整体机构的刚度
Fig.8 Stiffness of a tensegrity mechanism
由图8a和图8b可知,当θ1=90°、λ=0°时,刚度Kθ1、Kλ均处于最大值,而此时机构位姿处于图4b所示的初始平衡状态。当λ=30°、θ1=110°或λ=-32.2°、θ1=68°时,机构位姿分别处于图4a、图4c所示的稳定平衡状态,此时刚度Kθ1、Kλ均处于较大值。随着转动角度的变化,机构逐步失去平衡状态,机构刚度Kθ1、Kλ会逐渐减小,甚至变为负值。为了防止机构刚度缺失,保证机构正常工作,刚度Kθ1、Kλ必须大于0。
4.2 刚度分布
由机构正解方程(式(7)、式(8))可知,当机构处于平衡状态时,x、y、λ是关于驱动L1、L2的函数,将x、y、λ用关于L1、L2的函数表示,代入式(18)、式(19)可得到刚度Kθ1、Kλ关于L1、L2的表达式。机构在驱动工作空间中的刚度分布等高线图见图9。
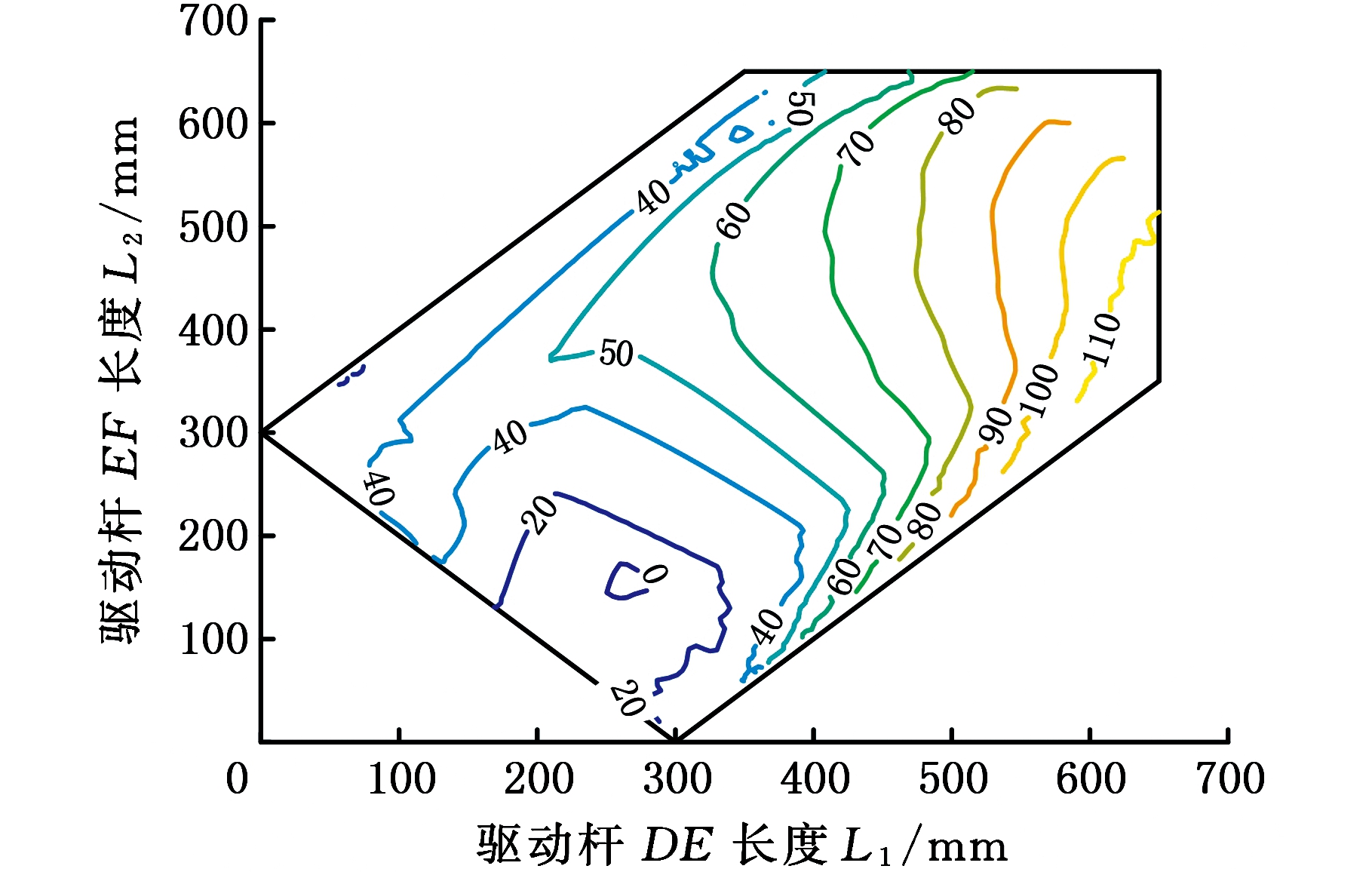
(a)刚度Kθ1分布

(b)刚度Kλ分布
图9 刚度在驱动工作空间的分布
Fig.9 Stiffness distributions in the drive workspace
由机构反解方程(式(4)、式(5))可知,输入变量L1、L2可通过输出变量x、y、λ表示,将x、y、λ代入反解方程可得到L1、L2关于变量x、y、λ的表达式,代入式(18)、式(19)可得刚度Kθ1、Kλ关于变量x、y、λ的表达式。机构在输出工作空间中的刚度分布等高线图见图10。
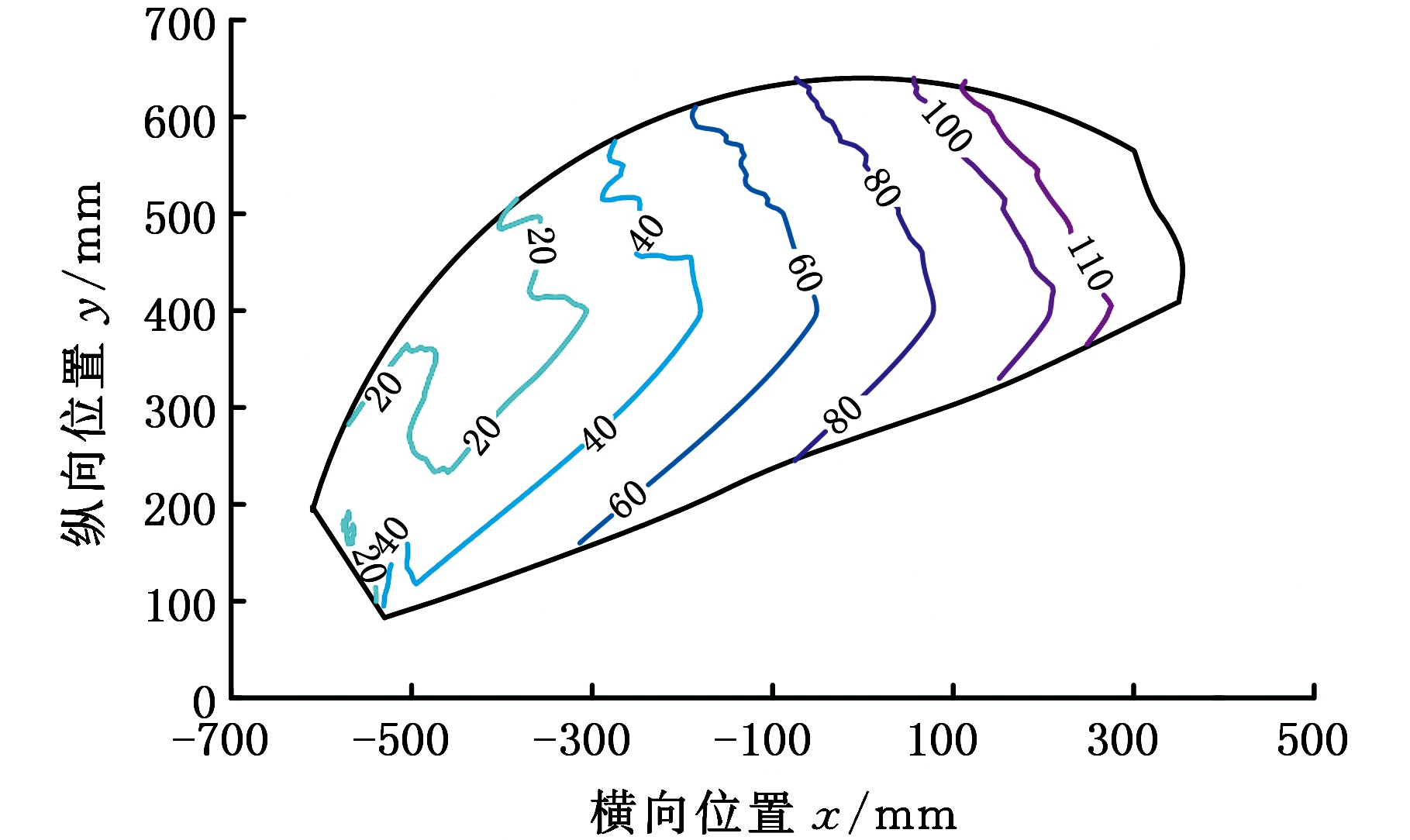
(a)刚度Kθ1分布
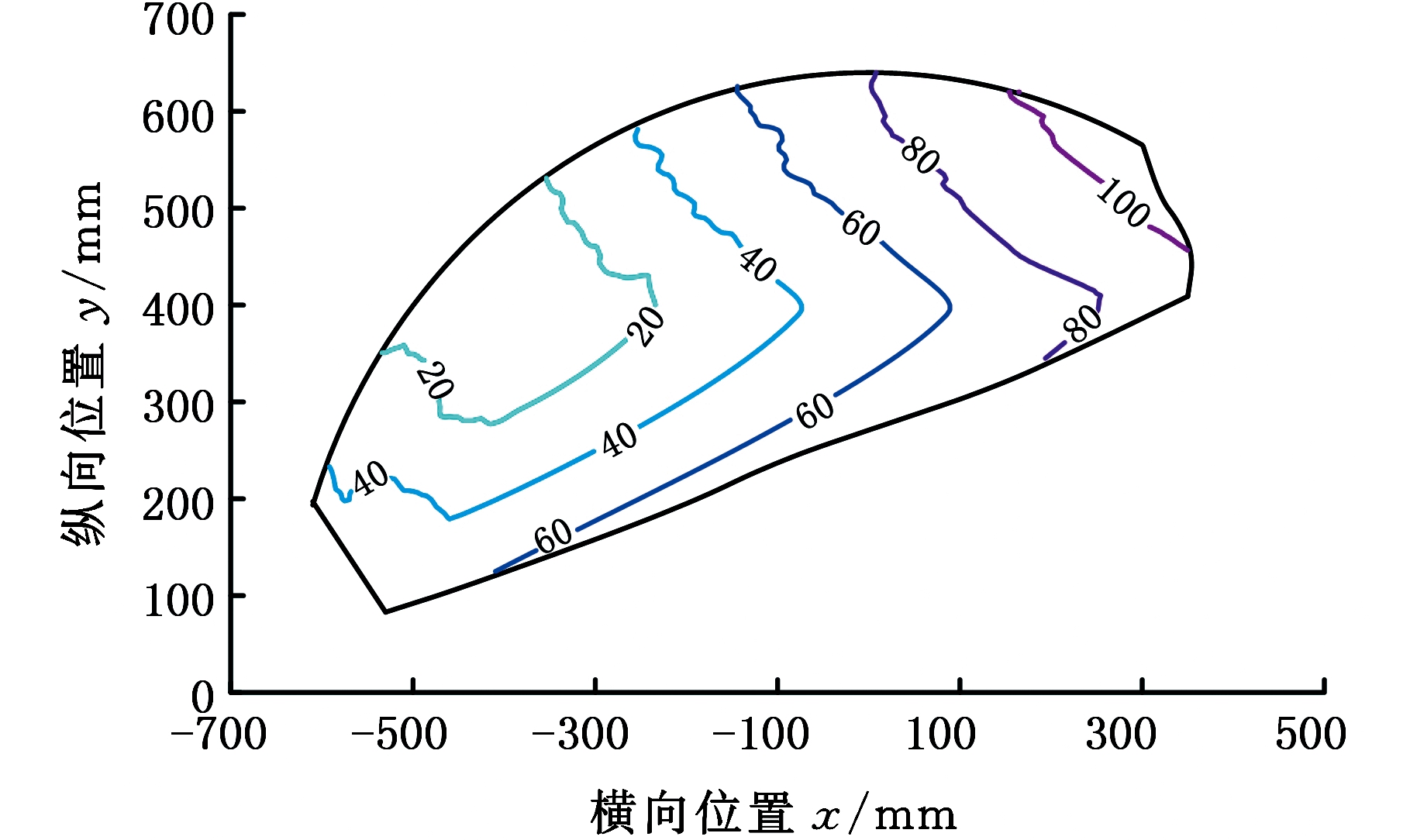
(b)刚度Kλ分布
图10 刚度在输出工作空间的分布
Fig.10 Stiffness distributions in the export workspace
图9、图10所示分别为刚度Kθ1、Kλ在驱动工作空间和输出工作空间中的分布。由图9a、图9b可知,当L1=260 mm、L2=180 mm时,机构的刚度Kθ1达到最小值0,而刚度Kλ则处于0~20 N·m/(°)范围内,随着驱动杆长不断地变化,机构的刚度Kθ1、Kλ随之发生变化。根据机构正解方程(式(7)、式(8))可求得,当L1=260 mm、L2=180 mm时,机构对应的输出参数为:x=-413.6 mm, y=371.2 mm,如图10a、图10b所示,此时机构的刚度Kθ1、Kλ均处于最小刚度值范围内,这也验证了上述推导的刚度模型是符合机构运动规律的。由此可见,机构的刚度在整个工作空间中具有较大的变化范围,刚度分布特征图可为机构的设计和应用提供较好的理论依据。
5 动力学分析
张拉整体机构主要具有动能和势能两种能量,mi(i=1,2,3,4)分别表示杆DE、EF、DF、BE的质量,驱动器和柔性构件的质量可忽略不计。根据拉格朗日方程对张拉整体机构进行动力学建模,并忽略机构的重力势能,其表达式如下:
q=(θ1,L1,L2)T Q=(Q1,Q2,Q3)T![]()


式中,q为广义坐标向量;Ek为机构的动能; Q为作用于机构系统的广义力向量,包含弹簧的阻尼力和驱动杆的驱动力;F1、F2分别为驱动杆DE、EF的驱动力;c1、c2分别为弹簧AD、CF的阻尼系数。
将机构总势能表达式(式(9))代入式(20),可得机构动力学模型的表达式为
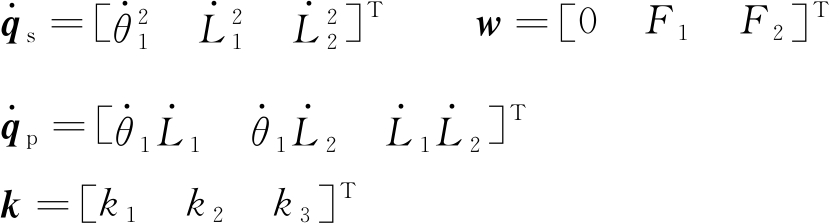
![]()
2aLsin αcos θ1)
k2=k(L1+Lcos(θ1-γ-θ2)-![]()
2acos(α+θ2+γ))
k3=k(L2+Lcos(θ1-θ2)-acos(α-θ2)-L1σ·![]()
其中,M为质量惯性矩阵,F为离心力矩阵,G为科氏力矩阵,H为重力矩阵,M、F、G、H均为3×3的矩阵,各矩阵元素 (如Mij 表示M矩阵的第i行第j列元素,其他类同 )分别可表示为

F11=F12=F21=F13=F31=0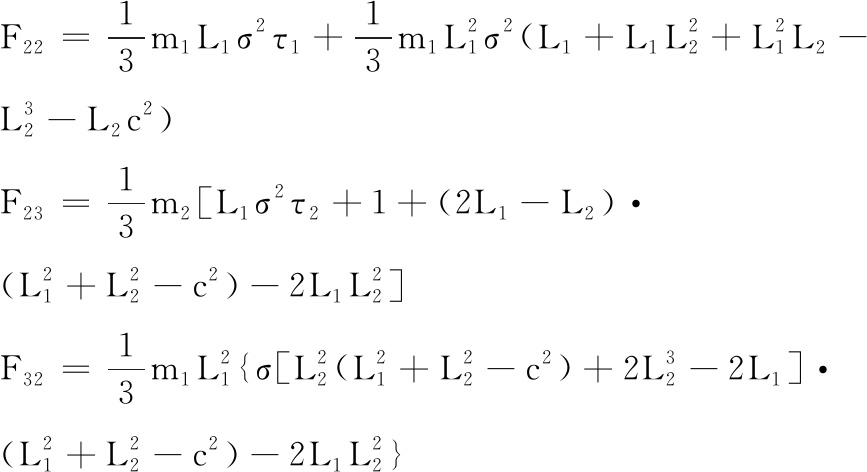
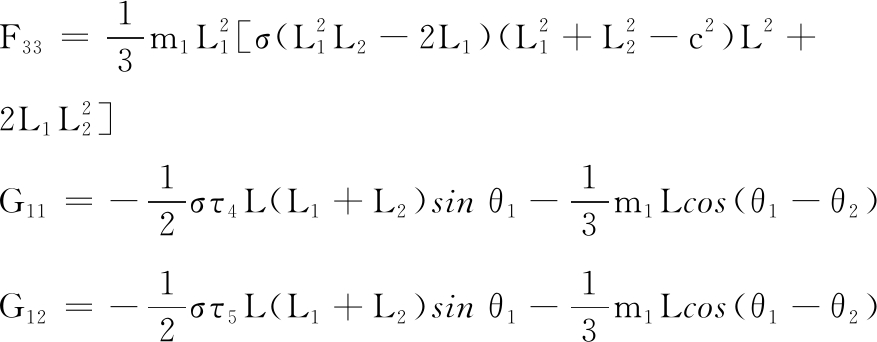
G13=0 G21=L1L2Lm3σcos θ1
G22=3LL2m2σcos θ1
2Lσsin(θ1-λ)
H12=H21=4c0asin(-λ+φ)-c0cσL1cos φ-
4c0Lσcos(θ1-λ+φ)![]()
L1L2cos(θ1-θ2)]![]()
H33=4c0m3L1σ(L1+L2+c2)![]()
τ1=![]()
τ2=![]()

其中,阻尼系数c1=c2=c0。
在平面张拉整体机构的三维模型中,机构几何参数的设置与前文相同,刚性杆的质量均设定为0.217 9 kg,弹簧刚度系数和阻尼系数分别设定为K1=K2=k=50 N/mm、c1=c2=c0=0.03 N·m/s。假设支链驱动杆的输入分别为
根据动力学模型的表达式(式(21)),采用MATLAB软件编程可得到驱动力计算结果以及采用ADAMS软件可得到仿真模拟的曲线,如图11所示,可以看出,仿真结果与计算结果基本一致,从而验证了动力学模型的正确性。
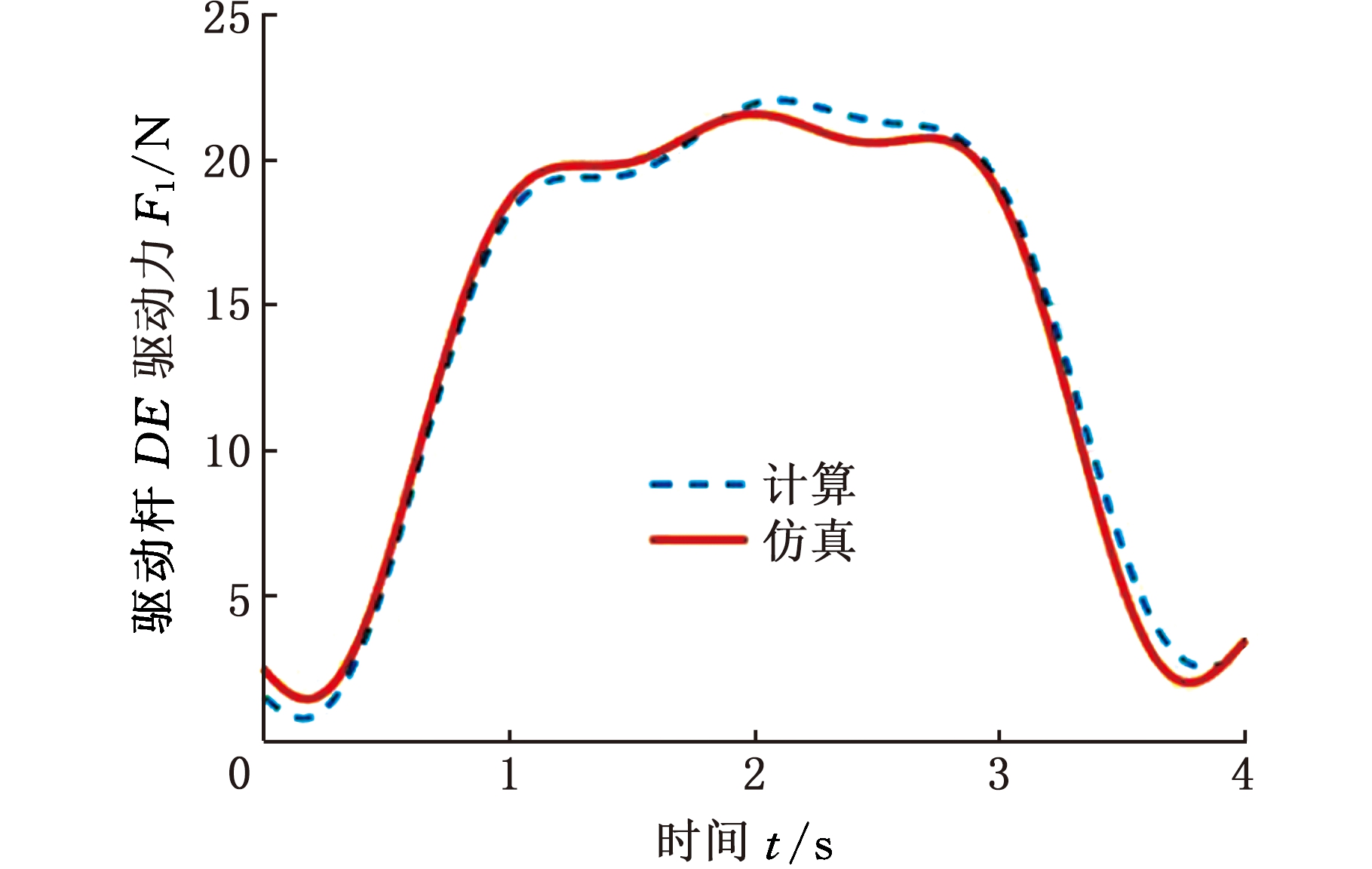
(a)杆DE驱动力曲线
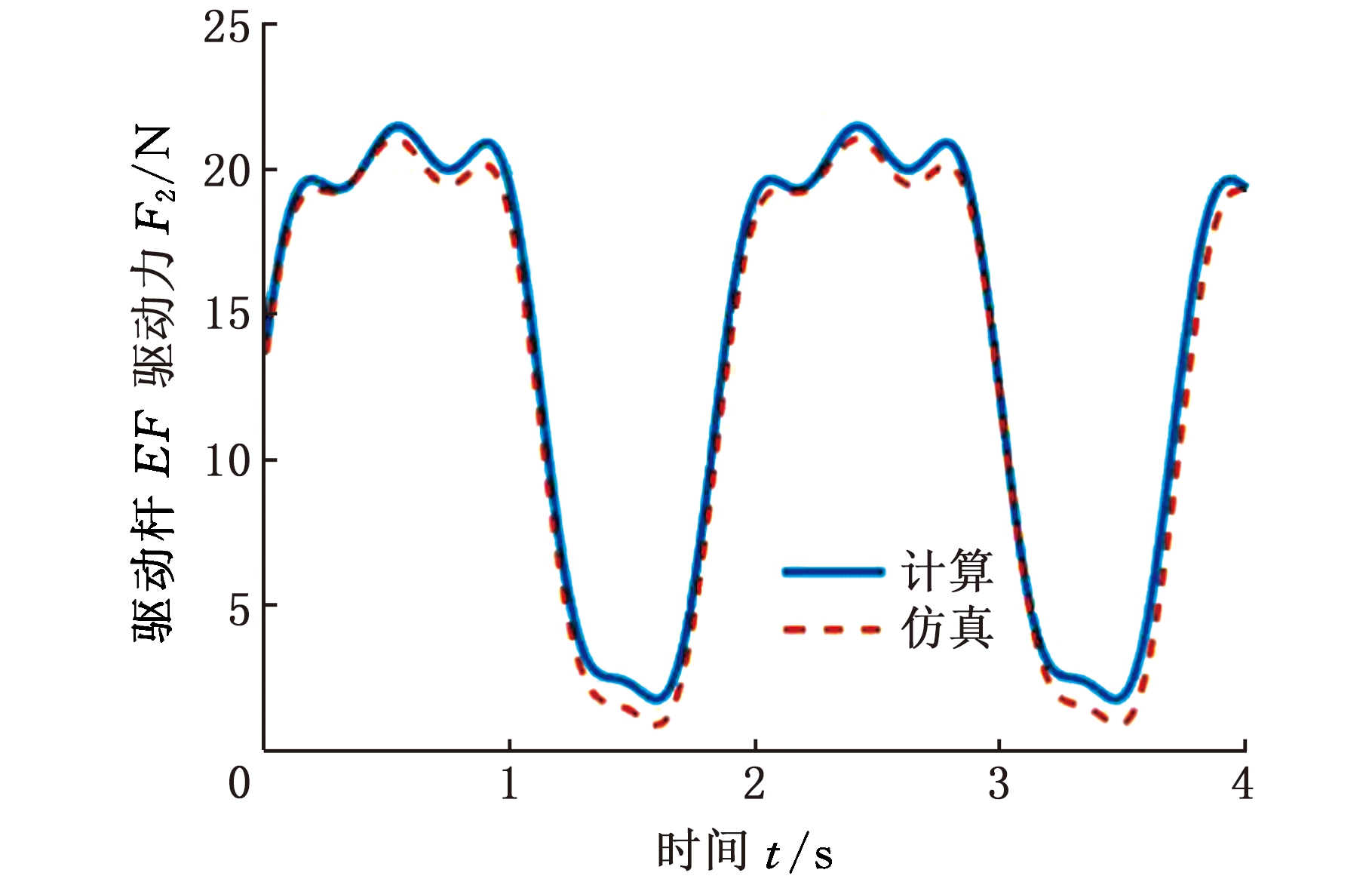
(b)杆EF驱动力曲线
图11 驱动力仿真与计算曲线
Fig.11 Simulation and calculation curves of driving forces
6 结论
(1)基于Assur杆组组成原理提出了一种平面张拉整体机构的拓扑结构综合方法,以一种两平移一转动机构为例,利用机构静力学特性求出了机构正反解方程,并通过数值方法进行了验证,研究结果表明,采用绝对瞬心法求反解和势能法求正解是可行的。
(2)分析了机构的奇异位形,根据运动学方程搜索出了对应的机构奇异位姿图,并根据机构的奇异位置关系得到了驱动工作空间和输出工作空间边界。
(3)研究了张拉整体机构在平衡状态下的转动刚度模型及其刚度值分布特征,分析了影响机构刚度的主要因素。
(4)建立了基于拉格朗日方程的机构动力学模型,由MATLAB软件数值计算得出了驱动杆的驱动力曲线,并通过ADAMS软件进行了模型仿真验证。
[1] 樊猛. 柔性机械臂路径优化及控制[D]. 西安:西安电子科技大学, 2010.
FAN Meng. Path Optimization and Control of Flexible Manipulator[D]. Xi’an: Xidian University, 2010.
[2] JUAN S H, TUR J M M. Tensegrity Frameworks: Static Analysis Review[J]. Mechanism & Machine Theory, 2008, 43(7):859-881.
[3] TUR J M M, JUAN S H. Tensegrity Frameworks:Dynamic Analysis Review and Open Problems[J]. Mechanism & Machine Theory, 2009, 44(1):1-18.
[4] SHEKARFOROUSH S M M, EGHTESAD M, FARID M. Kinematic and Static Analyses of Statically Balanced Spatial Tensegrity Mechanism with Active Compliant Components[J]. Journal of Intelligent & Robotic Systems, 2013, 71:287-302.
[5] VASQUEZ R E, CRANE C D, CORREA J C. Analysis of a Planar Tensegrity Mechanism for Ocean Wave Energy Harvesting[J]. Journal of Mechanisms & Robotics, 2014, 6(3):031015.
[6] ROVIRA A G, TUR J M M. Control and Simulation of a Tensegrity-based Mobile Robot[J]. Robotics and Autonomous Systems, 2009, 57(5):526-535.
[7] BAYAT J, CRANE C D. Closed-form Equilibrium Analysis of Planar Tensegrity Structures[C]∥ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Las Vegas,2007:13-23.
[8] ARSENAULT M, GOSSELIN C M. Kinematic,Static and Dynamic Analysis of a Planar 2-DOF Tensegrity Mechanism[J]. Mechanism & Machine Theory, 2006, 41(9):1072-1089.
[9] SHAI O, TEHORI I, BRONFELD A, et al. Adjustable Tensegrity Robot Based on Assur Graph Principle[C]∥ASME International Mechanical Engineering Congress & Exposition.Florida,2009:13-19.
[10] CHEN S, ARSENAULT M. Analytical Computation of the Actuator and Cartesian Workspace Boundaries for a Planar 2-Degree-of-freedom Translational Tensegrity Mechanism[J]. Journal of Mechanisms and Robotics, 2012, 47(1):455-466.
[11] JI Zhifei, LI Tuanjie, LIN Min. Kinematics, Workspaces and Stiffness of a Planar Class-2 Tensegrity Mechanism[J]. UPB Scientific Bulletin, 2014, 76(3):53-64.
[12] ABADI B N R, FARID M, MAHZOON M. Introducing and Analyzing a Novel Three-degree-of-freedom Spatial Tensegrity Mechanism[J]. Journal of Computational & Nonlinear Dynamics, 2014, 9(2):94-94.
[13] ABADI B N R, SHEKARFOROUSH S M M, MAHZOON M, et al. Kinematic, Stiffness, and Dynamic Analyses of a Compliant Tensegrity Mechanism[J]. Journal of Mechanisms & Robotics, 2014, 6(4):041101.
[14] SHEKARFOROUSH S M M, EGHTESAD M, FARID M. Design of Statically Balanced Six-degree-of-freedom Parallel Mechanisms Based on Tensegrity System[C] ∥ASME International Mechanical Engineering Congress and Exposition. Lake Buena Vista, 2009:245-253.
[15] ARSENAULT M, GOSSELIN C M. Kinematic and static analysis of a 3-PUPS spatial Tensegrity Mechanism[J]. Mechanism & Machine Theory, 2009, 44(1):162-179.
[16] 朱伟, 王传伟, 顾开荣,等. 一种新型张拉整体并联机构刚度及动力学分析[J].吉林大学学报(工学版),2018, 48(6):1777-1786.
ZHU Wei,WANG Chuanwei,GU Kairong,et al. Stiffness and Dynamics Analysis of a New Type of Tensegrity Parallel Mechanism[J].Journal of Jilin University (Engineering and Technology Edition), 2018, 48(6):1777-1786.
[17] 袁李. 基于四杆张拉整体结构的机器人研究[D]. 哈尔滨:哈尔滨工程大学, 2016.
YUAN Li. Research on the Robot Based on the Four-bar Tensioning Structure[D]. Harbin:Harbin University of Engineering, 2016.
[18] 沈惠平,强恒存,曾氢菲,等. 基于结构降耦的一类低耦合度新型3T1R并联机构的拓扑设计[J].中国机械工程,2017,28(10):1163-1171.
SHEN Huiping, QIANG Hengcun, ZENG Qingfei, et al. Topological Design for a Class of Novel 3T1R Parallel Mechanisms with Low Coupling Degree Based on Coupling-reducing[J]. China Mechanical Engineering, 2017,28(10):1163-1171.
[19] 朱伟, 戴志明, 刘晓飞,等. 一种新型弱耦合三平移并联机器人机构及其运动学分析[J], 中国机械工程,2017,28(13):1561-1566.
ZHU Wei, DAI Zhiming, LIU Xiaofei, et al. A Novel Weak-coupling Three-translation Parallel Robot Mechanisms and Its Kinematics Analysis[J]. China Mechanical Engineering, 2017, 28(13):1561-1566.
[20] SERVATIUS B, SHAI O, WHITELEY W. Geometric Properties of Assur Graphs[J]. European Journal of Combinatorics, 2010, 31(4):1105-1120.
