0 引言
复杂机械系统的结构优化往往涉及大量设计变量,需要探索广泛的设计空间。基于仿真的结构优化需要对结构性能响应进行大量的仿真计算,计算量过大、收敛速度缓慢甚至不收敛是结构优化设计存在的关键问题。近似模型方法通过少量的样本点信息拟合设计变量(系统输入)与性能响应(系统输出)之间的关系,从而替代复杂的仿真计算以达到缩短设计周期、减少设计成本的目的。
近似概念由SCHMIT等[1]于1974年首次提出,因其应用简单、计算速度快而被广泛应用于结构优化领域。SINGH等[2]利用计算流体动力学(computational fluid dynamics,CFD)仿真得到的数据建立了一个高保真度Co-Kriging近似模型,实现了气体旋流器的多目标优化;在此基础上,XIA等[3]提出一种自适应Co-Kriging近似模型,比传统Co-Kriging近似模型更为准确有效,结合启发式优化算法,成功应用于变压器绕组的优化设计中;蒋荣超等[4]利用Kriging函数建立了汽车行驶平顺性和操纵稳定性近似模型,基于NSGA-Ⅱ算法(elitist non-dominated sorting genetic algorithm, NSGA-Ⅱ)对汽车悬架系统进行了结构优化。2005年,ZERPA等[5]首次提出组合近似模型的概念,通过多个单一近似模型加权线性叠加构成组合近似模型,克服了单一近似模型的局限性,提高了近似模型的预测精度。潘峰[6]建立了表征组合近似模型拟合不确定性的评价指标,提出了考虑交叉验证误差均值和方差的组合近似模型权系数计算方法,并将该方法运用到轿车车身的轻量化设计中,取得了显著的效果。SHI等[7]利用支持向量回归(support vector regression,SVR)和Kriging函数建立了牙种植多学科组合近似模型,成功替代了种植界面应力值的有限元计算。
本文以某型号内燃叉车两级门架结构为研究对象,提出一种基于组合近似模型的轻量化设计方法。结合有限元技术和瞬态动力学理论对门架后倾工况进行仿真计算,采用熵权TOPSIS(technique for order preference by similarity to ideal solution)综合贡献度分析法研究外门架结构参数对性能响应的影响程度,并以此为依据筛选出用于轻量化设计的结构参数,利用最优拉丁超立方设计(optimal Lain hypercube design, Opt-LHD)方法在结构参数的变化范围内进行样本点采集,结合近似模型理论与二次序列规划算法对叉车门架展开轻量化设计,该方法可以应用到不同型号的叉车设计阶段,达到快速、高质量、低成本地生产新产品的目的。
1 近似模型优化理论
近似模型[8-10]是采用插值、拟合以及函数逼近技术,通过有限样本点的数据信息构建具有函数特性的设计变量与结构响应之间的近似关系,达到预测未知点处响应的数学方法。
利用建立的近似模型来替代复杂的仿真计算,以牺牲一定的计算精度为代价,可以大幅降低计算成本、缩短优化周期。常用的近似模型有传统多项式响应面(polynomial response surface, PRS)、Kriging函数、径向基函数(radial basis function, RBF)和支持向量回归(support vector machine, SVM)等[11-13],具体表达式如下。
多项式响应面模型:
式中,N为设计变量的个数;xi为第i个变量;a0、bi、cii、cij为待定系数。
Kriging函数:
![]()
式中,fi(x)为确定的多项式基函数;γi为未知系数;Z(x)为随机分布误差函数。
径向基函数:
式中,ri为输入样本x与第i个样本点xi的距离;c为控制参数;βi为第i个基函数加权系数;m为基函数的个数。
支持向量回归模型:
y=(w·Φ(xi))+b
(4)
式中,w∈Rn;x∈Rn,xi∈x;b∈R;(·)表示向量内积。
基于近似模型的轻量化设计流程如图1所示,包括建立优化模型、实验设计与采样、近似模型建立与误差验证、优化求解与仿真验证等。
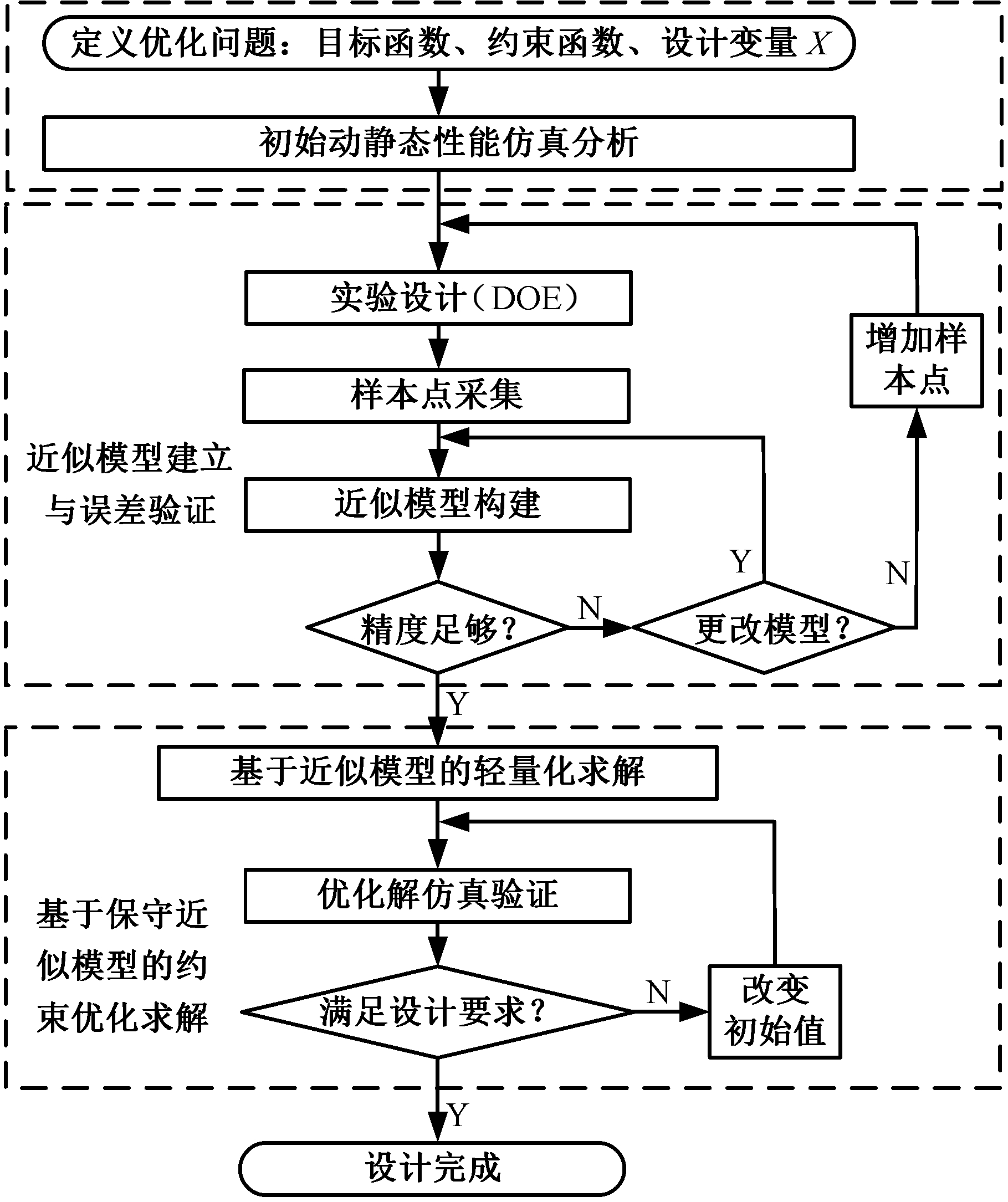
图1 基于近似模型的优化流程
Fig.1 Optimization process based on approximate model
2 门架瞬态动力学分析
叉车是物流装卸、堆垛、搬运环节的核心装备,门架是叉车承载重物的重要部件,新型叉车朝着大举力、高举升的方向发展,对门架的强度、刚度提出了更高的要求。本文以某型号内燃车两级门架为例进行研究,其结构如图2所示。
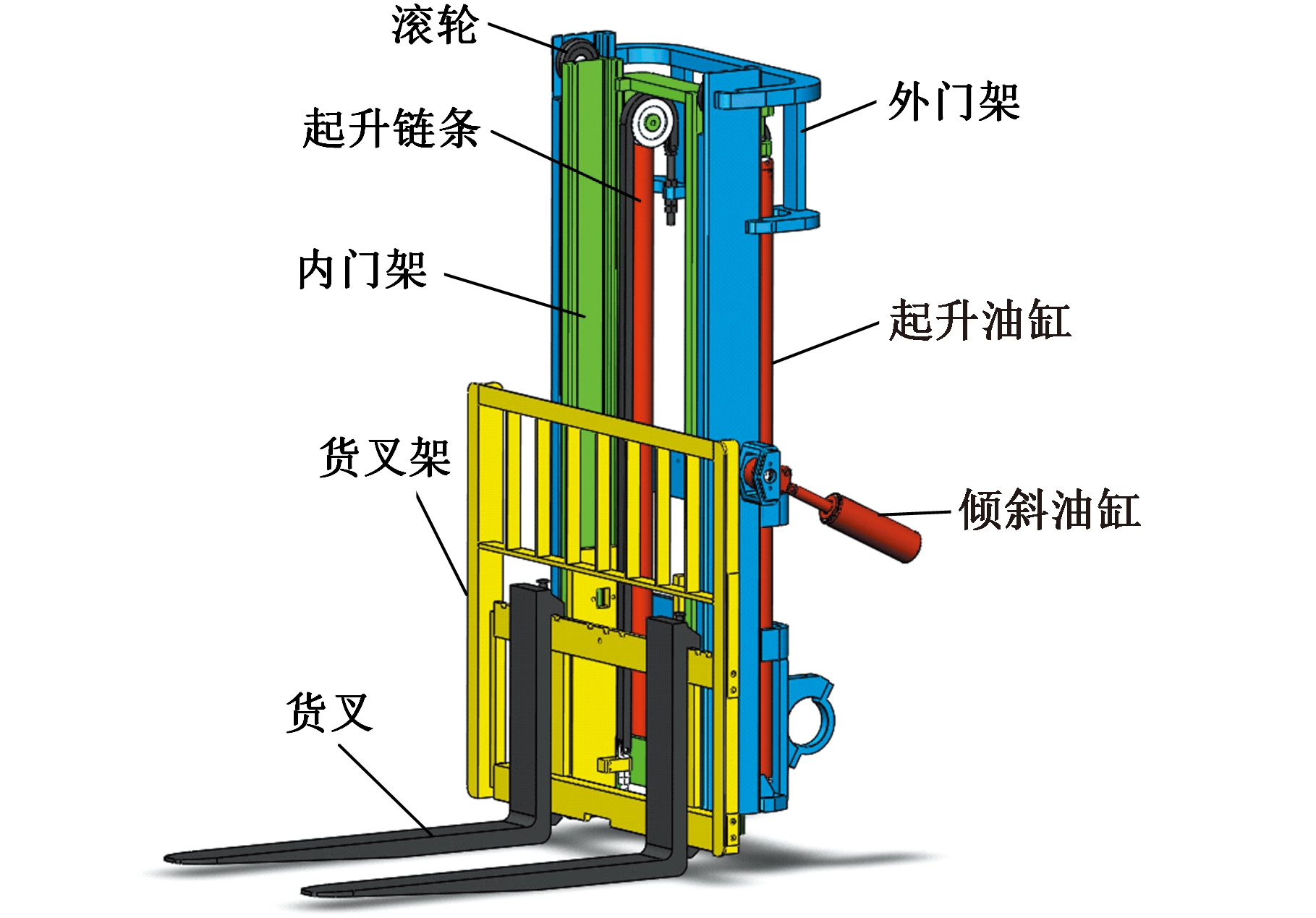
图2 叉车门架结构图
Fig.2 Forklift frame structure diagram
货叉架、内门架、外门架上均装有滚轮,货叉架以内门架为活动导轨、以滚轮为滚子实现上下运动;内门架以外门架为活动导轨,以滚轮为滚子实现上下运动;倾斜油缸推动门架整体实现前后倾斜运动。针对门架满载3 t起升至最高点的情况对倾斜油缸驱动下后倾6°的倾斜工况展开瞬态动力学分析。
门架材料为Q345,弹性模量E=206 GPa,密度ρ=7 850 kg/m3,屈服强度σs=345 MPa。货叉与货叉架之间的连接方式设置为刚性接触,滚轮与槽钢、倾斜油缸活塞与缸体之间为摩擦接触,摩擦因数取0.1,滚轮与轮轴、倾斜油缸与外门架之间为转动副连接。采用Solid92四面体实体单元划分网格,基于局部网格控制技术获得高质量的网格划分,得到506 650个节点,285 787个单元。为了使求解易于收敛,将各个载荷分为3步缓慢加载,求解时间设置为3 s,子步数设置为10。求解得到门架应力云图、变形云图以及在后倾过程中的最大应力、最大位移随时间变化曲线,见图3。由有限元分析结果可以看出,门架在后倾作业工况中,各部件的最大应力值均小于材料的许用应力345 MPa,在倾斜油缸匀速推动阶段,各部件的最大应力值趋于稳定,表明门架倾斜角度对最大应力的影响不大。
3 外门架轻量化设计
3.1 设计变量贡献度分析
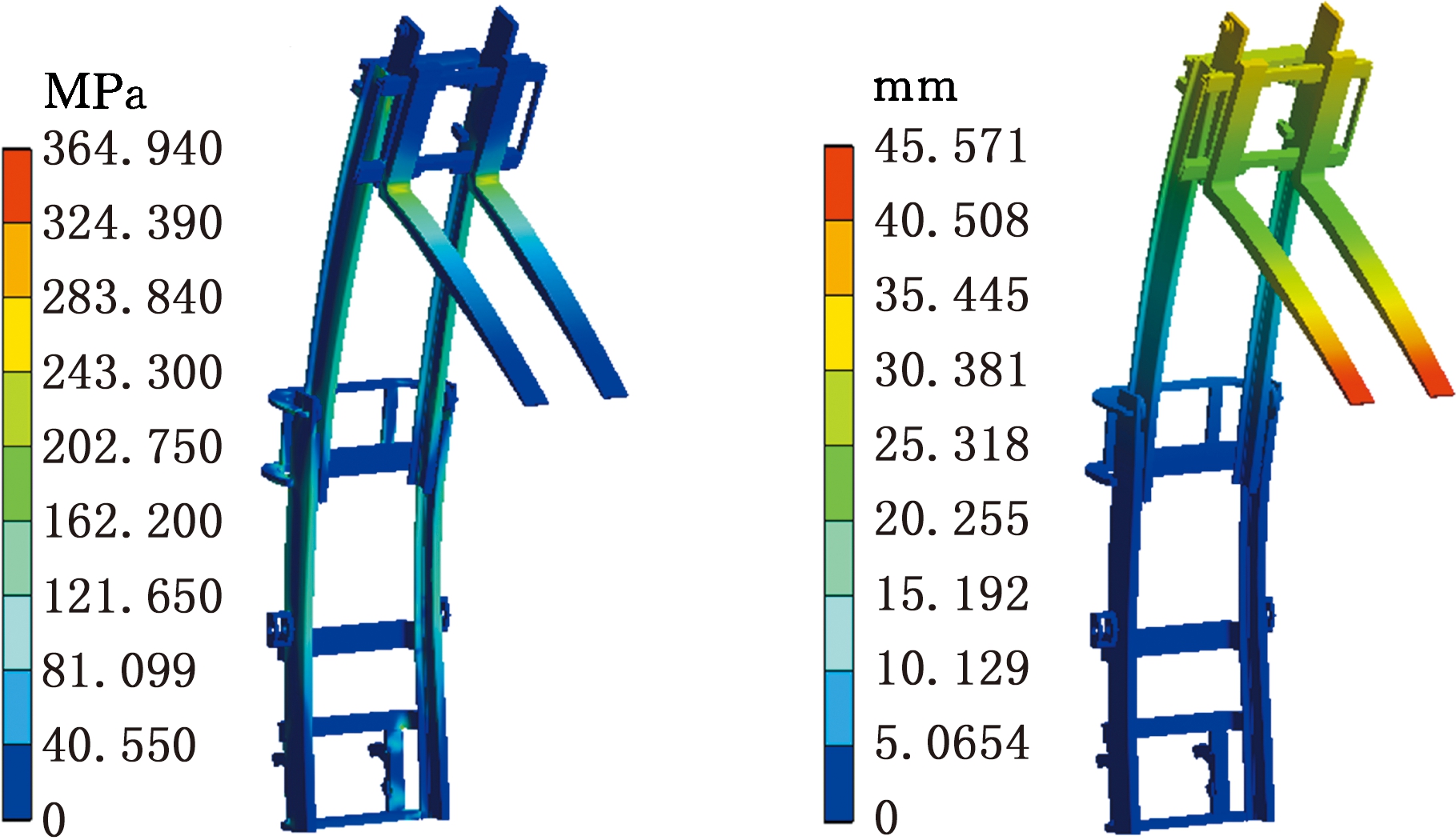
(a)应力云图 (b)变形云图
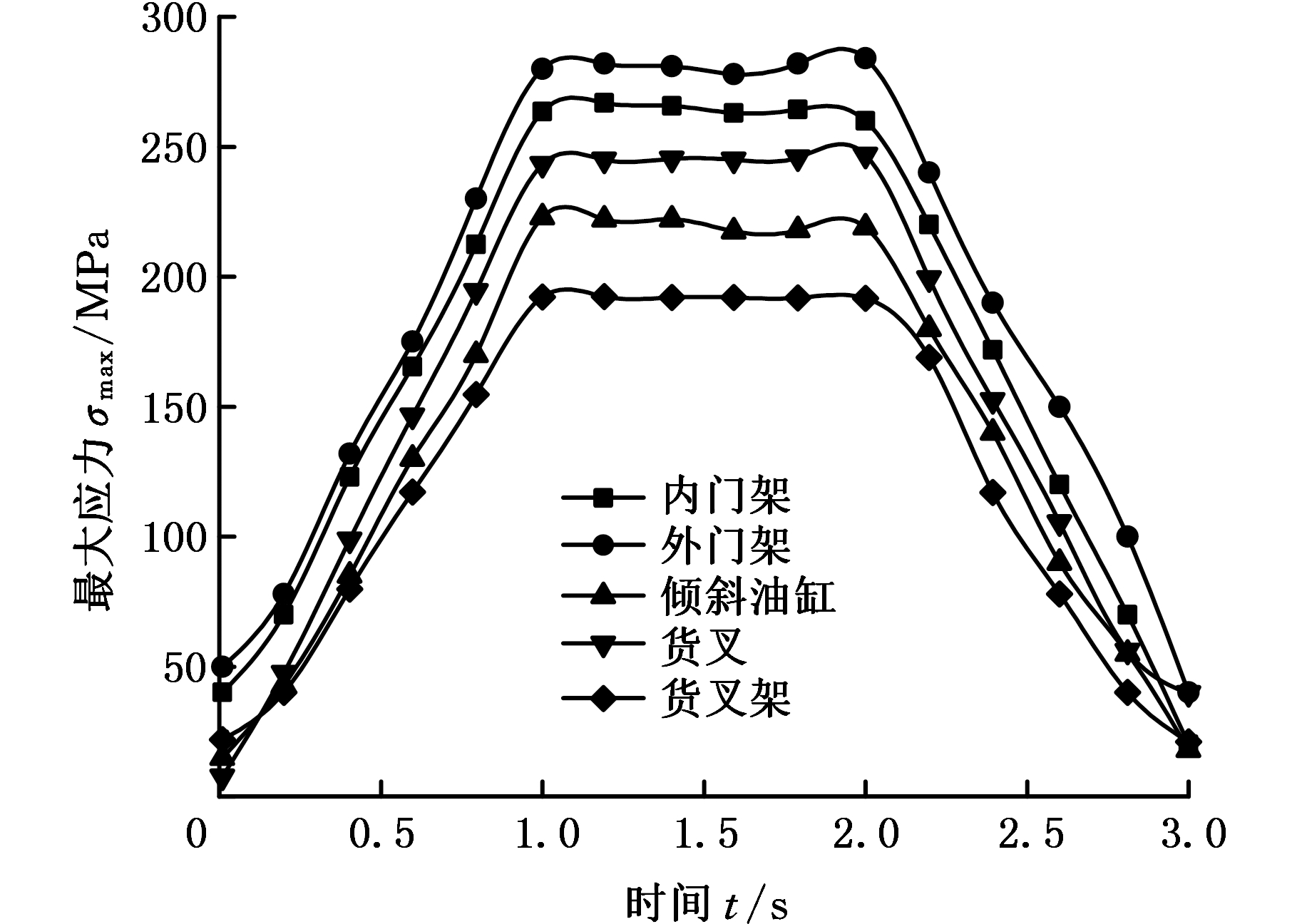
(c)最大应力随时间变化曲线
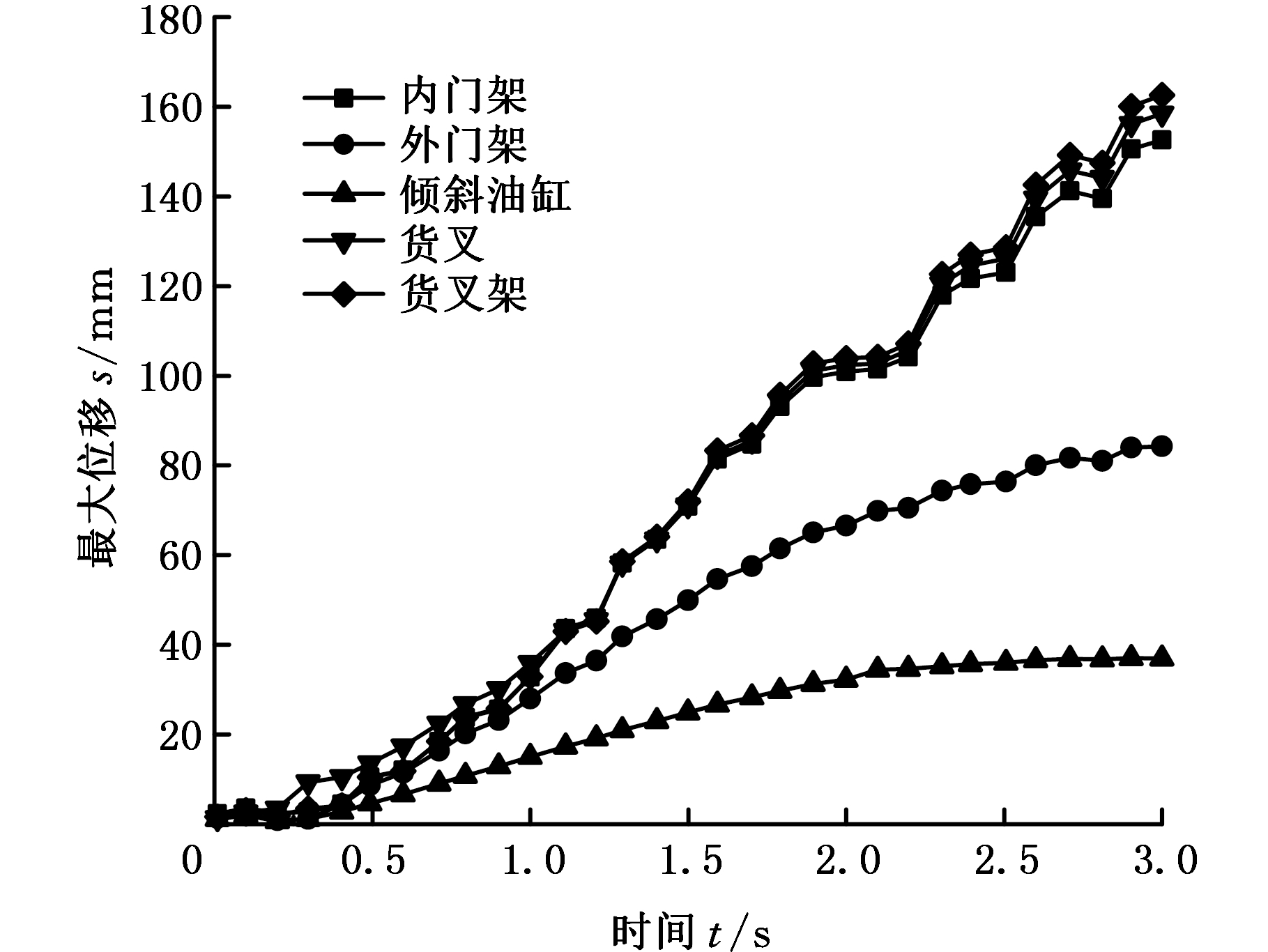
(d)最大位移随时间变化曲线
图3 门架瞬态动力学分析结果
Fig.3 Transient dynamics analysis results of frame structure
从门架瞬态动力学分析结果可以看出,门架应力、变形等性能皆有富余,具有很大的轻量化设计空间。本文以外门架为例,基于组合近似模型的优化方法展开轻量化设计。外门架主要是由立柱、上横梁、中横梁、下横梁、油缸座以及铰接孔焊接而成的,这些零件的厚度变量和宽度变量是外门架主要的设计参数,选取对外门架质量影响较大的立柱上翼缘厚度x1、立柱下翼缘厚度x2、立柱腹板厚度x3、铰接孔厚度x4、油缸座厚度x5、下横梁厚度x6、中横梁厚度x7、链条连接板厚度x8、肋板厚度x9、上横梁厚度x10等10个设计参数,如图4所示。
采用正交试验设计方法对10个设计变量进行贡献度分析。各设计变量的初始值以及上下浮动5 mm作为3个水平,根据正交表L27(310)安排的设计变量进行有限元分析,通过门架额定载荷最大起升高度工况计算外门架质量M、最大应力S、最大变形G的变化特性,得到外门架10个设计变量对性能响应的贡献度如图5所示。
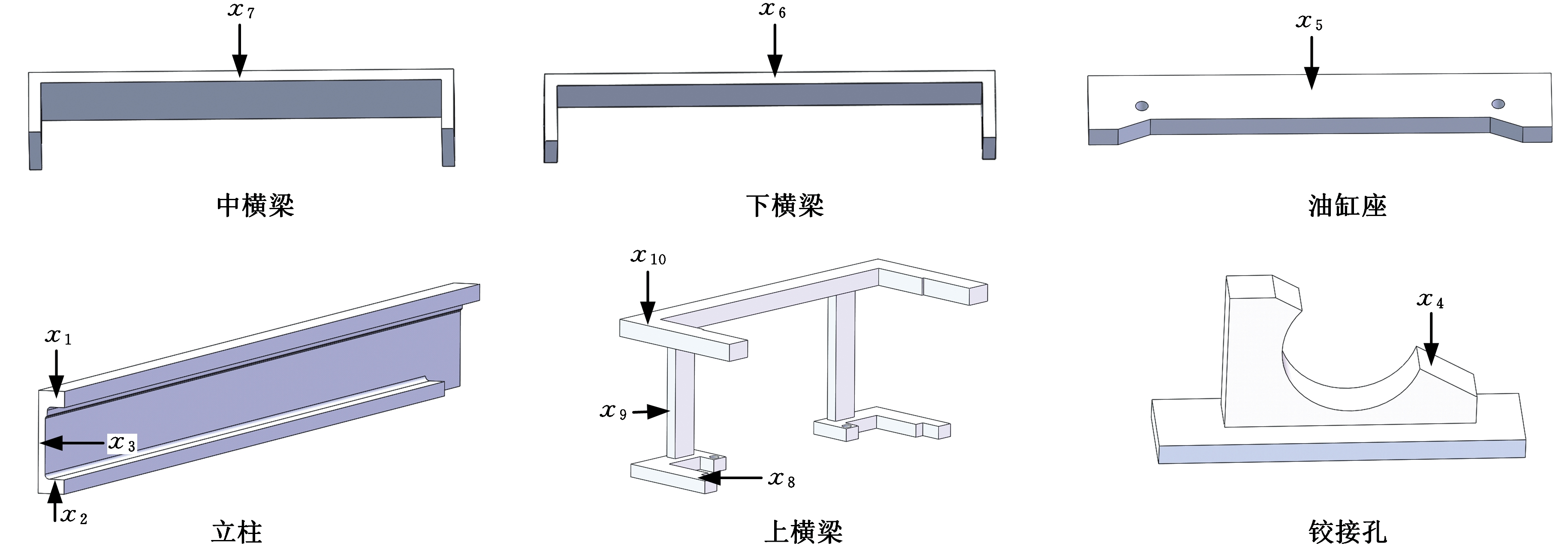
图4 外门架设计变量
Fig.4 External gantry design variables
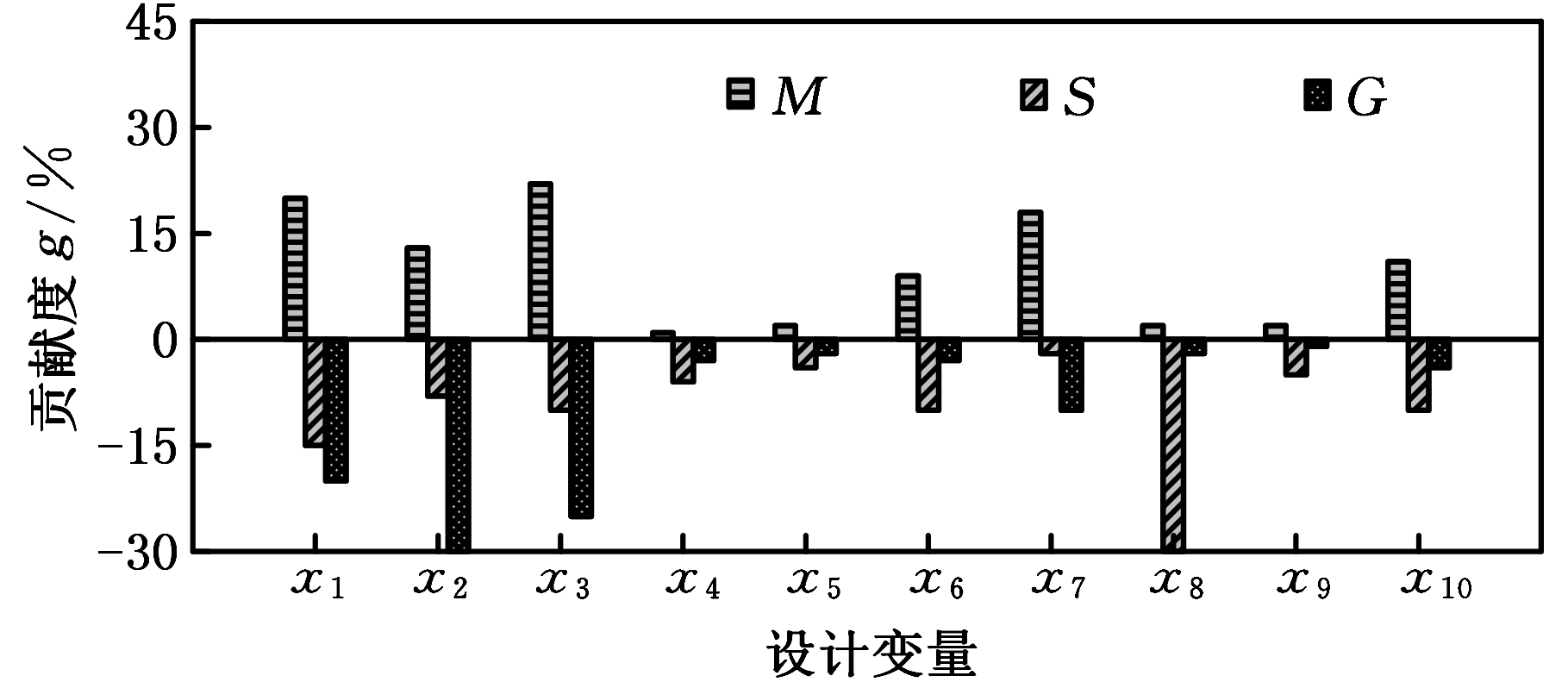
图5 设计变量对性能响应的贡献度
Fig.5 Contribution of design variables to performance response
从图5中可以看出,外门架立柱上下翼缘厚度x1、x2、腹板厚度x3以及上中下三个横梁的厚度x10、x7、x6对整体质量影响较大,链条连接板厚度x8对最大应力的影响最大,其余变量对外门架每个性能的贡献度大小各不相同。仅仅根据正交实验设计的贡献度分析结果很难进行设计变量的筛选,因为在轻量化设计中,每个性能指标的重要程度并不相同,质量M作为目标函数,相对于最大应力S和最大变形G,其重要程度要更大一些。
3.2 基于熵权TOPSIS的综合贡献度计算
利用TOPSIS方法可以将多性能响应问题转换为单性能响应问题。通过熵权法计算外门架3个性能响应的权重系数:

式中,wj为第j个性能响应的权重系数;ej为第j个性能响应的信息熵;n为性能响应的个数。
将设计变量对性能响应贡献度的绝对值作为TOPSIS方法的决策矩阵,并对其进行正则化处理,再与计算得到的权重系数wj相乘,得到加权决策矩阵:
V=(vij)m×n
(6)
按照下式计算理想解与负理想解:
式中,![]() 分别为第j个性能指标下的理想解与负理想解。
分别为第j个性能指标下的理想解与负理想解。
利用欧氏距离计算结构参数与理想解和负理想解之间的距离,根据距离大小对其进行排序:

式中,![]() 为结构参数与理想解的距离;
为结构参数与理想解的距离;![]() 为结构参数与负理想解的距离。
为结构参数与负理想解的距离。
每个参数对外门架性能响应的综合贡献度定义为
Ci为第i个变量对外门架性能的综合贡献度,其值越大表明该设计变量对外门架性能影响越大。外门架10个设计变量的综合贡献度分析结果如图6所示。
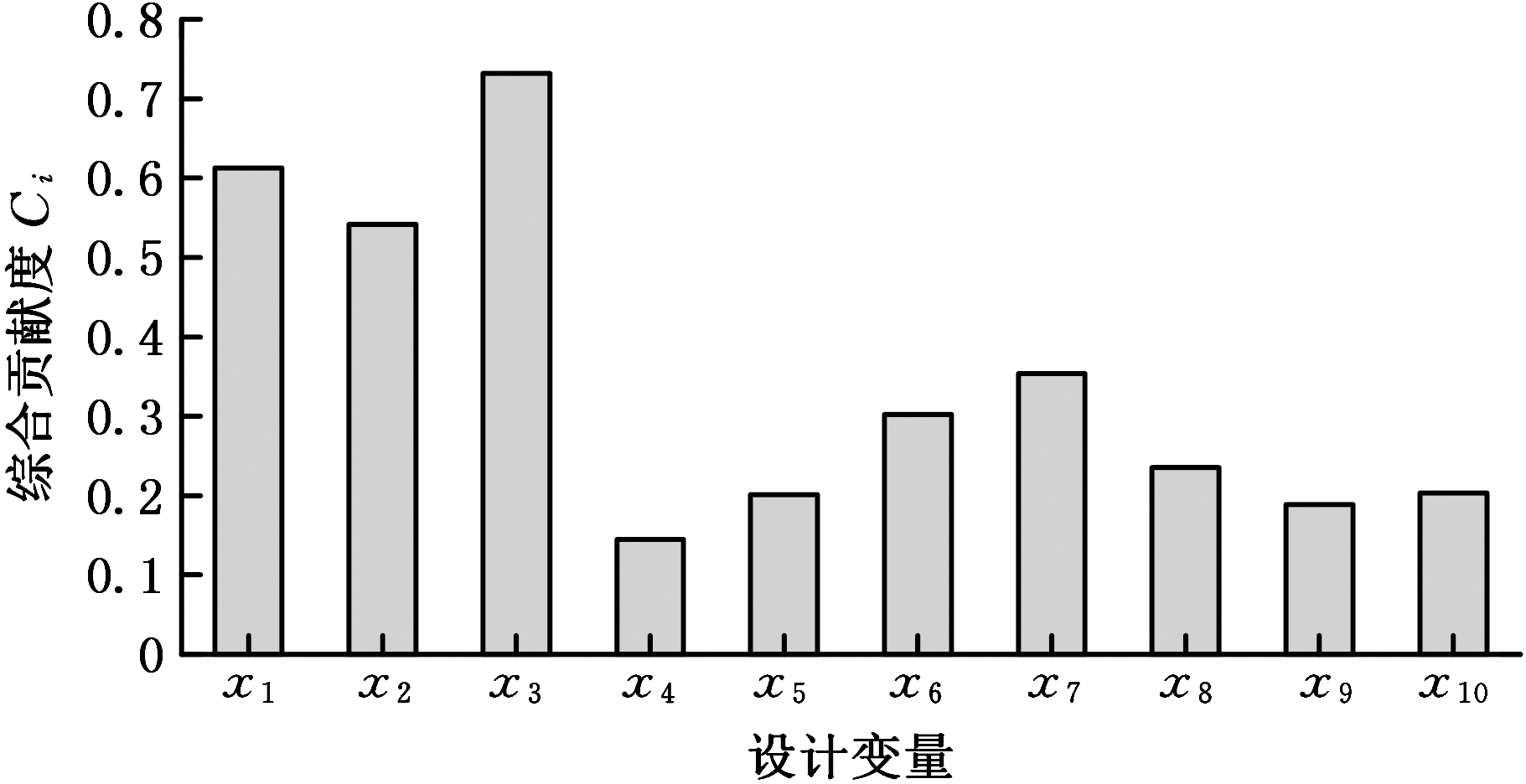
图6 设计变量对性能响应的综合贡献度
Fig.6 Comprehensive contribution of design variables to performance response
3.3 优化模型的建立
由熵权TOPSIS综合贡献度分析结果可以看出,外门架立柱上下翼缘厚度x1、x2和腹板厚度x3对性能响应的综合贡献度较高,因此将x1、x2、x3确定为优化设计变量。以外门架最大应力S、最大变形G为约束条件,外门架材料许用应力为345 MPa,取安全系数为1.5,计算得到最大应力S的范围为[0,230]MPa。外门架顶端许用位移fa=L/200,L为外门架的长度,取安全系数为1.5,计算得到外门架最大变形G的范围为[0,6.38]mm。以外门架整体质量为优化目标,综合考虑应力、变形等性能指标,以门架立柱截面厚度为设计变量,建立门架轻量化设计数学模型如下:
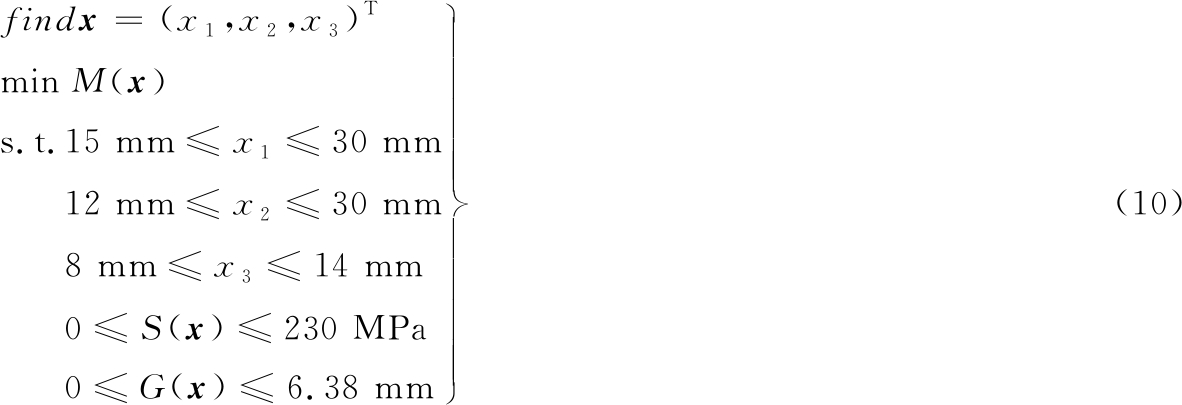
式中,x1、x2、x3为设计变量;M(x)为外门架质量;S(x)为外门架最大应力;G(x)为外门架最大变形。
3.4 组合近似模型的建立
单一近似模型往往只能拟合某一类优化问题,门架应力、变形与设计变量的响应关系非常复杂,为了获得更好的预测效果,采用多个单一近似模型通过加权线性叠加的方式构成组合近似模型:
式中,yEN为组合近似模型的预测值;m为用来构造组合近似模型的单一近似模型个数;ωi(x)为权系数,其和等于1;yi(x)为单一近似模型的预测值。
采用组合近似模型交叉验证均方差最小化方法计算权系数,将权系数计算过程当作优化问题处理,以权系数ωi为设计变量,以交叉验证均方差为目标函数,计算过程可以描述为

式中,EEN为组合近似模型的交叉验证均方差;yEN为组合近似模型的预测值;ya为实际响应值。
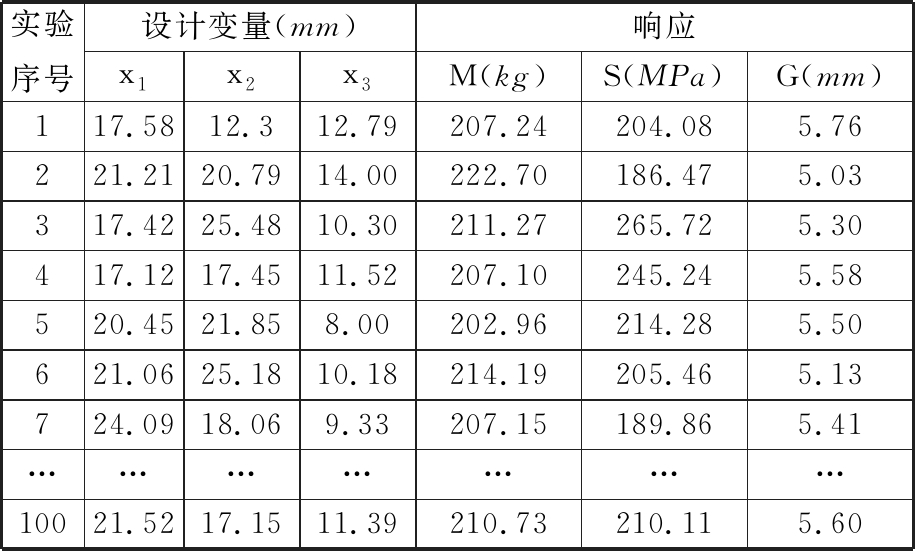
根据实际情况,确定三个设计变量的取值范围为:15 mm≤x1≤30 mm,12 mm≤x2≤27 mm,8 mm≤x3≤14 mm。为了获得均匀分布的样本点,采用最优拉丁超立方实验设计方法在设计空间内进行样本点采集,获得100个设计样本点。利用采集到的样本点数据建立外门架参数化模型,基于有限元分析技术计算外门架的最大应力、最大变形,部分样本点数据如表1所示。
根据最优拉丁超立方实验设计方法采样得到的100个设计样本点,利用90个样本点,采用响应曲面法(RSM)、RBF、Kriging三个单一近似模型构造外门架质量M、最大应力S、最大变形G的组合近似模型,剩余10个样本点用来检验组合近似模型的精度。建立后的组合近似模型三维曲面如图7所示。根据曲面图可以很好地观察到x1、x2、x3与M、S、G之间的响应关系。
表1 部分样本点数据信息
Tab.1 Part sample point data information
实验序号设计变量(mm)响应x1x2x3M(kg)S(MPa)G(mm)117.5812.312.79207.24204.085.76221.2120.7914.00222.70186.475.03317.4225.4810.30211.27265.725.30417.1217.4511.52207.10245.245.58520.4521.858.00202.96214.285.50621.0625.1810.18214.19205.465.13724.0918.069.33207.15189.865.41…………………10021.5217.1511.39210.73210.115.60
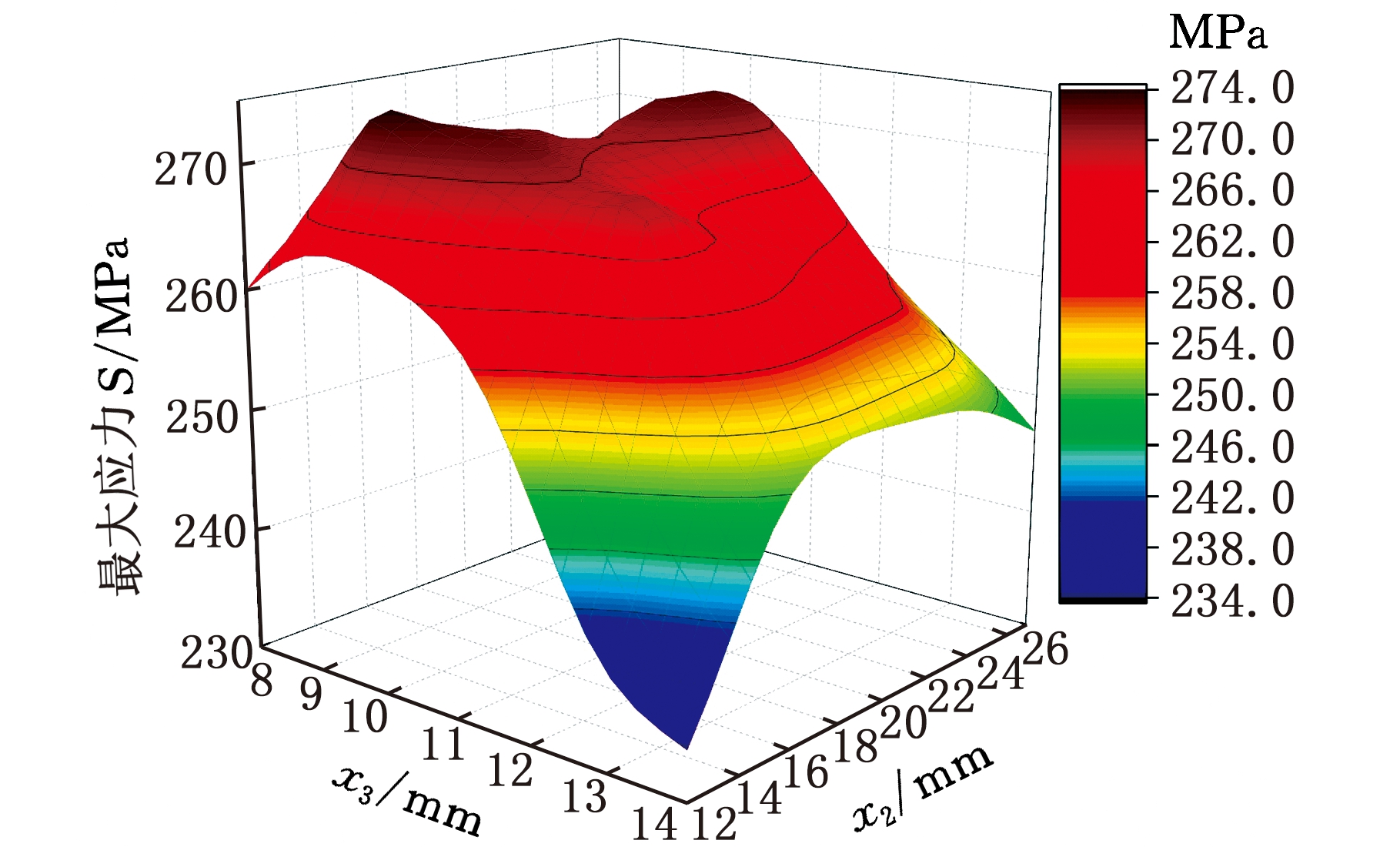
(a)x2、x3与S的响应曲面
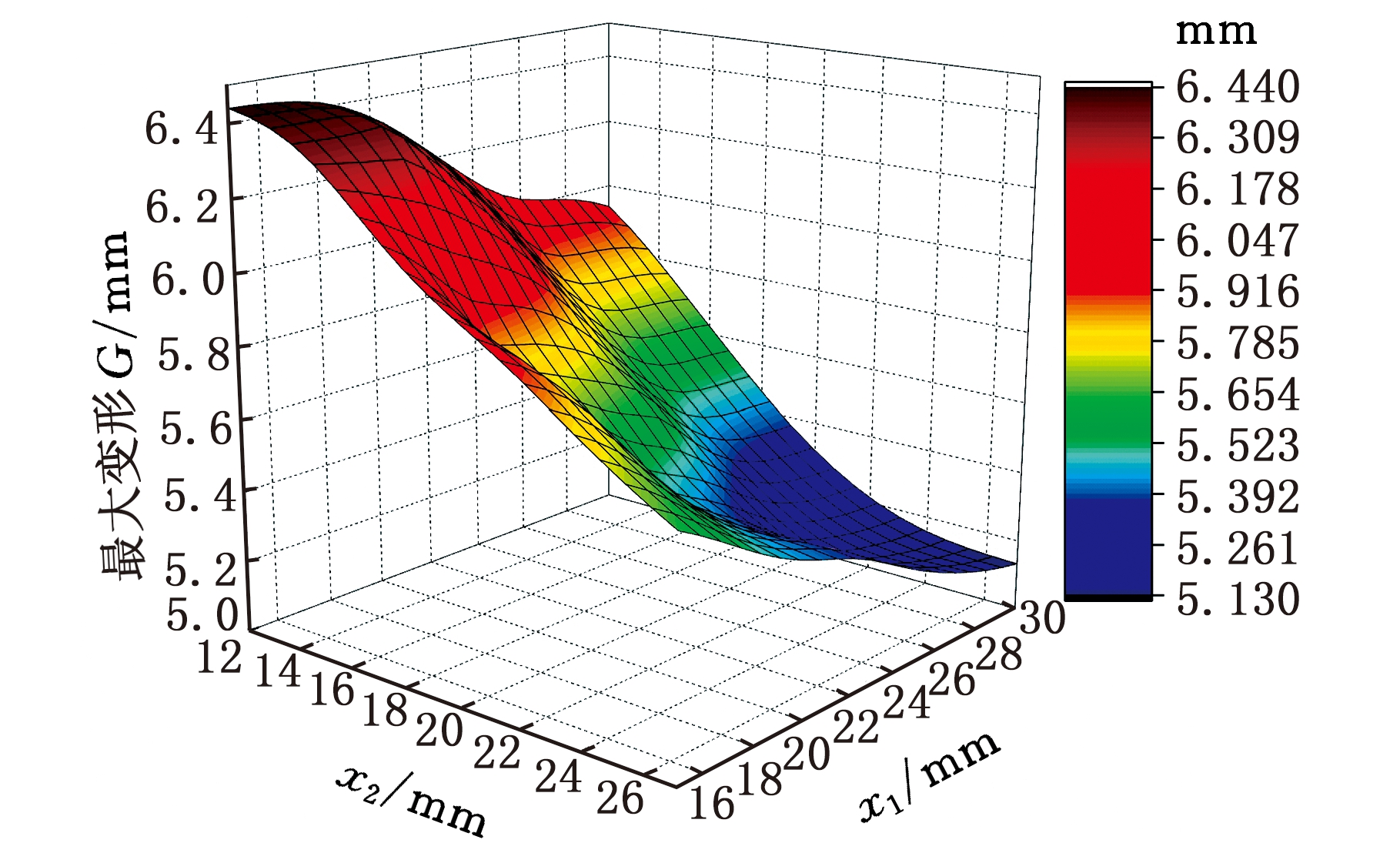
(b)x1、x2与G的响应曲面
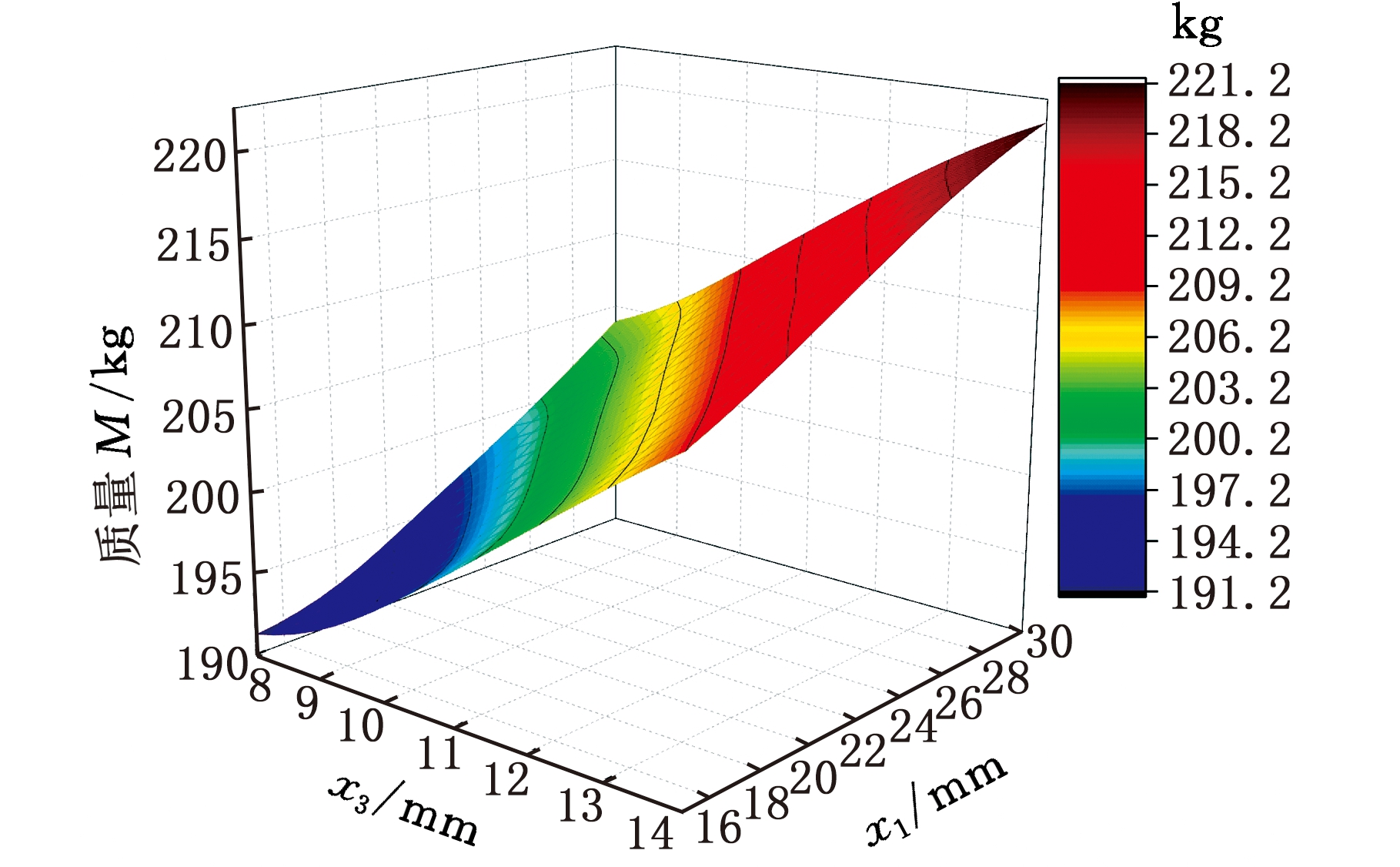
(c)x1、x3与M的响应曲面
图7 组合近似模型三维曲面
Fig.7 The 3D surface of combined approximation model
3.5 误差分析
为了保证优化结果的准确性,需要将近似模型的精度控制在一定范围内。近似模型误差分析指标主要有确定性系数R2、均方根误差ERMSE、最大绝对值误差EMAE、相对均方根误差ERRMSE和相对最大绝对值误差ERMAE,计算公式分别为


式中,yi为样本点的真实响应值;![]() 为根据近似模型计算得到的预测响应值;
为根据近似模型计算得到的预测响应值;![]() 为真实响应的平均值;Ne为用于检验近似模型精度的样本点个数;σ为yi的标准差。
为真实响应的平均值;Ne为用于检验近似模型精度的样本点个数;σ为yi的标准差。
使用确定性系数R2来评估近似模型的预测精度,一般认为当R2>0.9时,所建立的近似模型精度是可靠的,其值越接近于1则表明近似模型的精度越高;如果R2小于0.9,则需要更换近似模型或者增加新的样本点进行拟合,以此提高精度。组合近似模型误差分析结果如图8所示。根据误差分析结果,所建立的三组近似模型确定性系数R2均大于0.9,能够起到很好的预测效果。其中质量近似模型的精度接近1,变量与响应基本成线性关系,拟合起来相对比较容易。
3.6 优化结果
基于Isight平台搭建外门架轻量化设计流程,将质量M设置为目标函数,限定最大应力和最大位移的变化范围,采用二次序列规划算法求解组合近似模型,目标函数的迭代收敛曲线见图9。
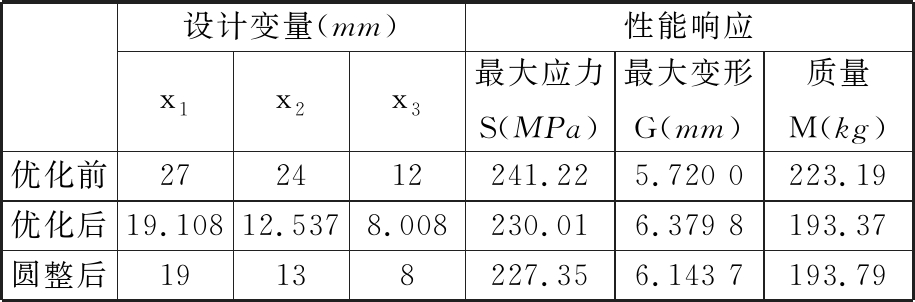
经过多次迭代求解,目标函数逐渐收敛于193.37 kg,得到最优解。经过优化,外门架质量减小13.36%,最大应力减小4.65%,虽然最大变形增大11.5%,但仍在允许范围之内。将优化后各设计变量的取值圆整后进行仿真计算,得到的圆整后的性能响应与近似模型的预测值相差不大。具体优化结果如表2所示。
4 结论
(1)以某型号内燃叉车两级门架结构为研究对象,采用组合近似模型的优化方法开展了轻量化设计。对门架后倾工况进行了瞬态动力学分析,发现最大应力出现在滚轮与槽钢的动态接触区域,其余部分应力值与材料许用应力相差甚远,具有很大的优化空间。
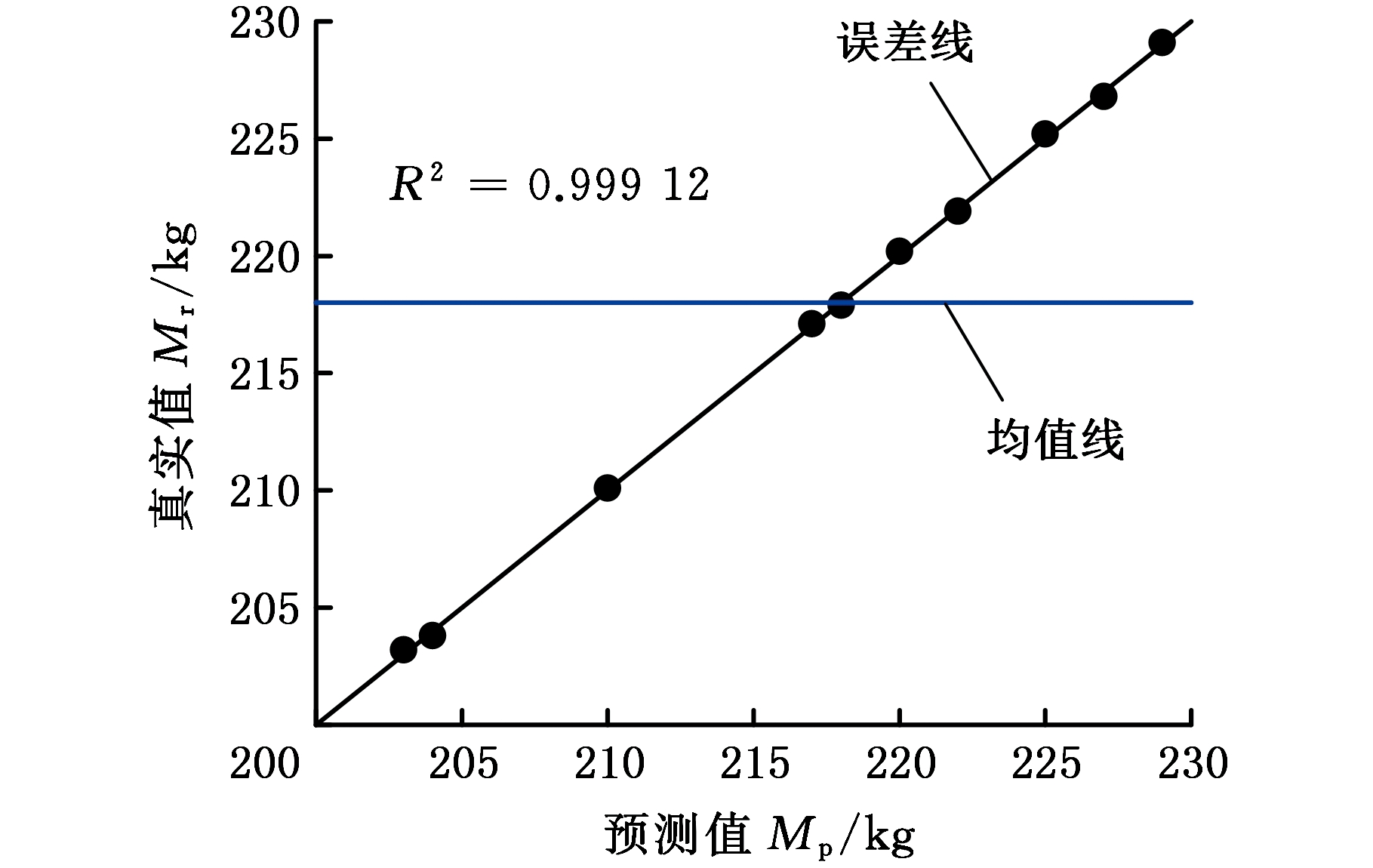
(a)门架质量
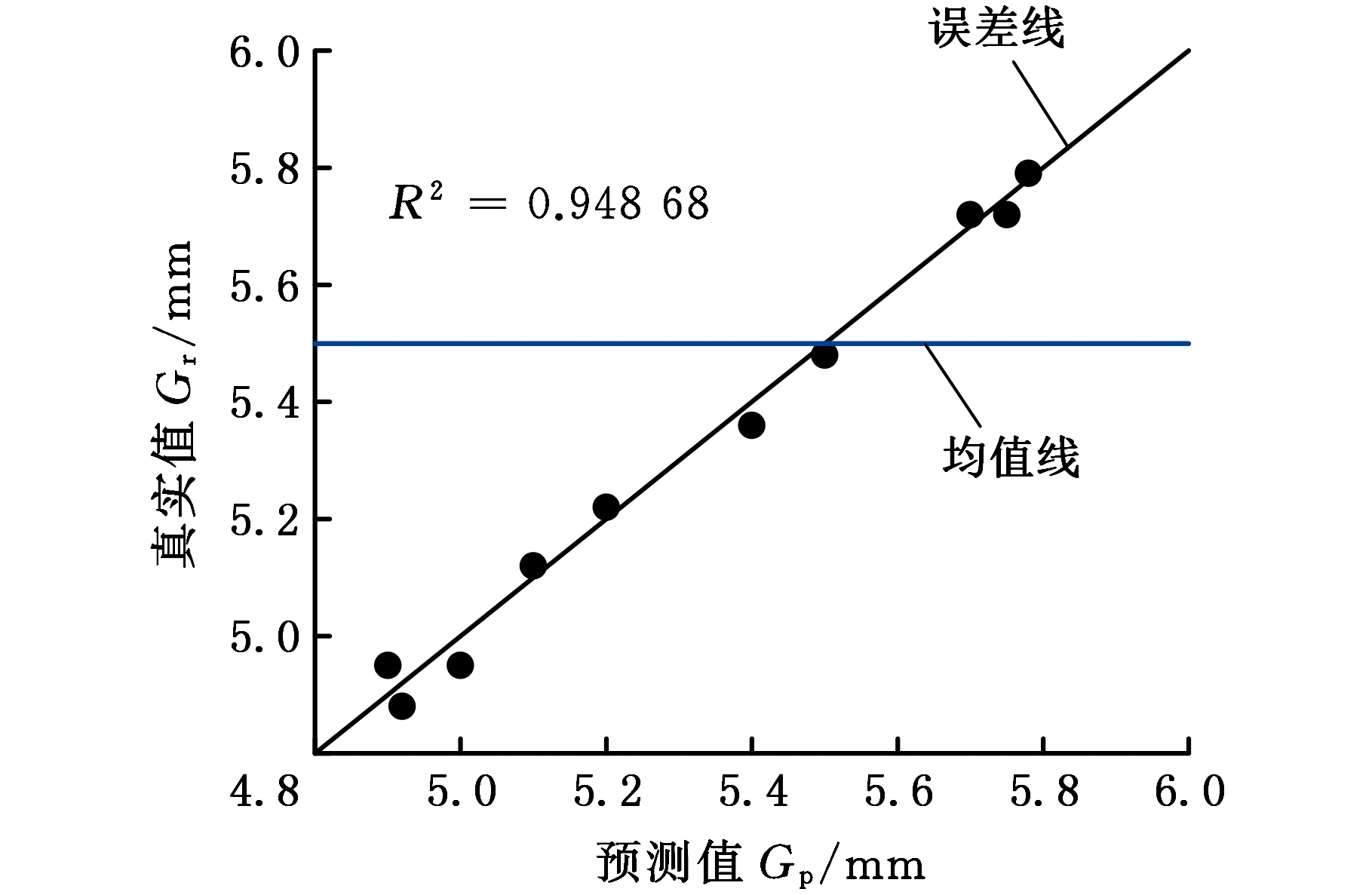
(b)最大变形
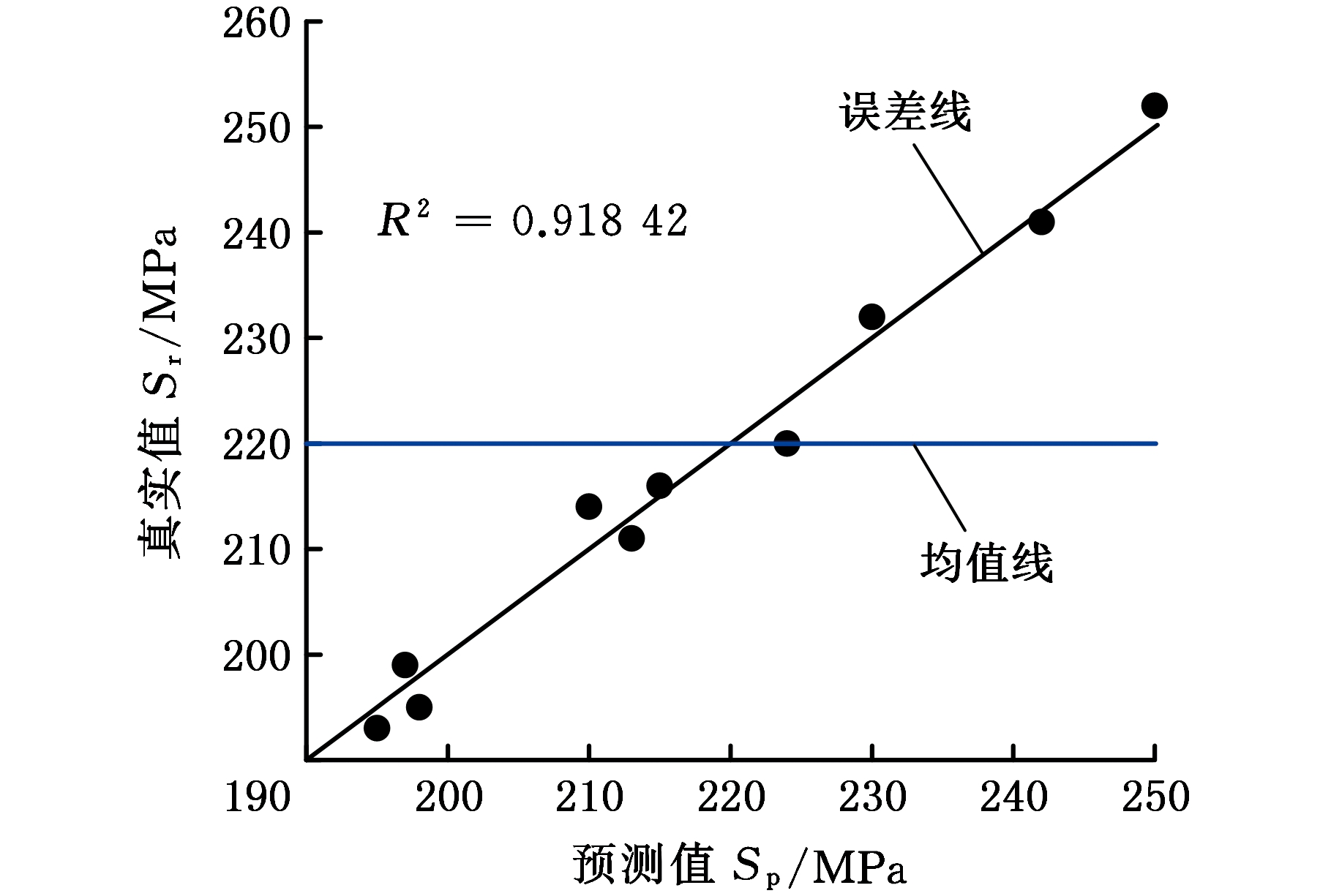
(c)最大应力
图8 组合近似模型误差分析结果
Fig.8 The error analysis results of combined approximation model
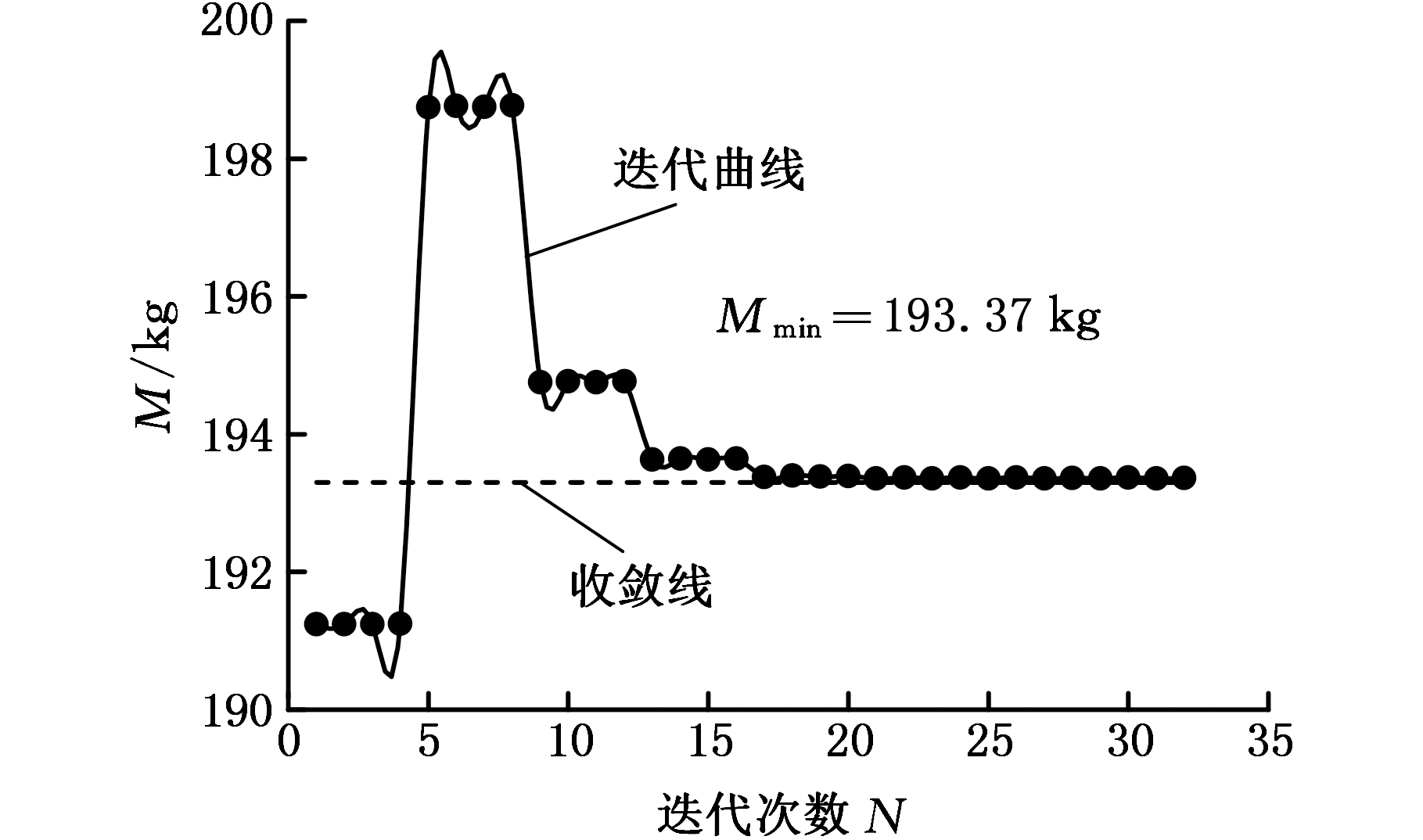
图9 目标函数迭代曲线
Fig.9 The iteration curve of objective function
表2 外门架优化结果
Tab.2 External gantry optimization results
设计变量(mm)性能响应x1x2x3最大应力S(MPa)最大变形G(mm)质量M(kg)优化前272412241.225.720 0223.19优化后19.10812.5378.008230.016.379 8193.37圆整后19138227.356.143 7193.79
(2)采用熵权TOPSIS综合贡献度分析方法对外门架10个设计变量进行贡献度分析,发现门架立柱上下翼缘及腹板厚度3个设计变量对门架性能性能影响最大。
(3)建立了外门架质量、最大应力、最大变形与设计变量的组合近似模型,采用二次序列规划算法求解模型,使得外门架质量减小13.36%,最大应力减小4.65%,轻量化效果显著;最大变形增大11.5%,但仍在允许范围之内。
[1] SCHMIT L A, FARSHI B, Some Approximation Concepts for Structural Synthesis[J]. Journal of AIAA, 1974,12:692-699.
[2] SINGH P, COUCKUYT I, ELSAYED K, et al. Multi-objective Geometry Optimization of a Gas Cyclone Using Triple-Fidelity Co-Kriging Surrogate Models[J]. Journal of Optimization Theory and Applications, 2017,175(1):172-193.
[3] XIA Bin, HONG S, CHOI K, et al. Optimal Design of Winding Transposition of Power Transformer Using Adaptive Co-kriging Surrogate Model[C]∥Electromagnetic Field Computation. Miami:IEEE, 2017:7203904.
[4] 蒋荣超,刘大维,王登峰.基于熵权TOPSIS方法的整车动力学性能多目标优化[J].机械工程学报,2018,54(2):150-158.
JIANG Rongchao, LIU Dawei, WANG Dengfeng. Multi-objective Optimization of Vehicle Dynamics Performance Based on Entropy Weighted TOPSIS Method[J]. Journal of Mechanical Engineering, 2018,54(2):150-158.
[5] ZERPA L E, QUEIPO N V, PINTOS S, et al. An Optimization Methodology of Alkaline-surfactant-polymer Folding Processes Using Field Scale Numerical Simulation and Multiple Surrogates[J]. Journal of Petroleum Science and Engineering, 2005, 47:197-208.
[6] 潘锋. 组合近似模型方法研究及其在轿车车身轻量化设计的应用[D].上海:上海交通大学,2011.
PAN Feng. Ensemble of Surrogate Models for Lightweight Design of Autobody Structure[D]. Shanghai: Shanghai Jiao Tong University, 2011.
[7] SHI Maolin, LI Hongyou, LIU Xiaomei . Multidisciplinary Design Optimization of Dental Implant Based on Finite Element Method and Surrogate Models[J]. Journal of Mechanical Science and Technology, 2017, 31(10):5067-5073.
[8] RUMPFKEIL M P, BERAN P. Construction of Dynamic Multifidelity Locally Optimized Surrogate Models[J]. AIAA Journal,2017, 55(6):1-11.
[9] LIU Bo, GROUT V, NIKOLAEVA A. Efficient Global Optimization of Actuator Based on a Surrogate Model Assisted Hybrid Algorithm[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7):5712-5721.
[10] LIU Bo, YANG Hao, LANCASTER M J. Global Optimization of Microwave Filters Based on a Surrogate Model-assisted Evolutionary Algorithm[J]. IEEE Transactions on Microwave Theory and Techniques, 2017,65(6):1976-1985.
[11] LIU Jun, SONG Wenping, HAN Zhonghua, et al. Efficient Aerodynamic Shape Optimization of Transonic Wings Using a Parallel Infilling Strategy and Surrogate Models[J]. Structural and Multidisciplinary Optimization,2017, 55(3):925-943.
[12] LI Hongxia, LIU Tao, WANG Minjie, et al. Design Optimization of Stent and Its Dilatation Balloon Using Kriging Surrogate Model[J]. Biomedical Engineering Online, 2017, 16(1):13.
[13] YUE Xianghuo, LI Yongle, LIAO Haili, et al. An Adaptive Surrogate Model Based on Support Vector Regression and Its Application to the Optimization of Railway Wind Barriers[J]. Structural and Multidisciplinary Optimization,2017, 55(2):701-713.
