0 引言
随着能源价格的不断上涨和环境问题的日益严峻,节能、减排、降成本已成为许多工厂管理者关注的热点。近年来,许多电力能源供应商已经开始实施分时电价制度,电价因时段不同呈现出明显差异。可重入混合流水车间调度问题是经典的混合流水车间调度和可重入调度二者的综合,所有的工件在各个工位之间都有相同的处理路径,并且以相同的顺序来回加工多次。可重入混合流水车间调度问题(re-entrant hybrid flow shop scheduling problem,RHFSP)广泛应用于一些特殊行业,如薄膜晶体管液晶显示器(TFT-LCD)面板制造、印刷电路板(PCB)以及半导体晶圆制造等。由于RHFSP涉及工序和设备较多,大多为高耗电量行业,因此依据分时电价机制来合理安排生产也是降低能耗成本的重要途径。RHFSP是一个典型的NP-hard问题[1],用精确的算法很难求解,因此开发求解RHFSP智能优化算法具有重要的理论意义和工程应用价值。
自1983年GRAVES等[2]首次对可重入调度问题展开研究,到目前该领域的研究已取得较大进展。CHEN等[3]提出了混合禁忌搜索算法求解以最小化最大完工时间为目标的RHFSP。KIM等[4]研究了每个阶段具有不相关并行机的RHFSP,提出了CDS和NEH启发式算法,以最小化最大完工时间和总拖期时间为优化目标。El-KHOULY等[5]利用拉格朗日分解法进行可重入流水车间调度优化的研究,并以最小化总拖期时间为优化目标。HEKMATFAR等[6]提出了一些启发式算法和随机密钥遗传算法求解以最小化最大完工时间为目标的RHFSP,并与混合遗传算法进行了对比研究。SHEN等[7-8]提出了改进教学优化算法(mTLBO)和基于Pareto的离散和声搜索算法(P-DHS)求解双目标的RHFSP。综上所述,在以往的RHFSP研究中优化目标通常以加工时间相关指标为主,很少考虑能耗成本以及碳排放问题,从而导致了理论研究与实际应用之间的巨大差距。
近年来环境污染问题日益加剧,温室气体的排放量逐年增加,全球变暖问题日益突出。在这些温室气体中,二氧化碳是全球变暖的主要因素,与工业化前相比,空气中二氧化碳的浓度增加了40%,已经超过了安全限值。据统计,工业部门大约消耗了世界能源总量的一半[9],在德国,制造业的能耗约占总能耗的47%以上,在中国,制造业的能耗占全国电力能源的50%[10]。同时,不断上涨的能源价格和当前的可持续发展趋势给制造企业带来了新的压力。面对这种局面,制造业需要采取有效的措施减少生产过程中的能耗和碳排放。绿色车间调度优化研究进展可参考文献[11]。DING等[12]提出了多目标NEH算法和迭代贪心算法求解置换流水车间调度问题,同样以最小化总碳排放量和最大完工时间为目标。艾子义等[13]采用新型邻域搜索算法求解以碳排放为目标的混合流水车间调度问题。PIROOZFARD等[14]针对柔性作业车间调度问题提出了改进的多目标进化算法,以最小化碳排放和总延迟为目标。PIROOZFARD等[15]还提出了一种多目标帝国竞争算法求解作业车间调度问题,以最小化碳排放和总延迟为目标。现有关于绿色调度的研究大都以碳排放作为优化目标,并且假定能源价格是恒定不变的,很少有考虑在能源价格可变情况下如何实现绿色生产。
根据分时电价政策合理安排生产,也是企业降低能耗成本的重要途径。在分时电价机制下,无需在生产设备和生产技术上投入大量资金,只需合理地调整生产任务,便能以极小的代价改善能源的利用情况,因此研究分时电价机制下车间调度问题具有十分重要的意义。LUO等[16]提出了一种多目标蚁群优化算法求解分时电价下不相关并行机混合流水车间调度问题,其目标是最小化最大完工时间和能耗成本,同时分析了关键参数对调度结果的影响。WANG等[17]在考虑能耗和需求的情况下,研究了分时电价下的制造模型。MOON等[18]提出了两个离散时间数学模型求解分时电价下以最大完工时间和电力成本加权和为目标的柔性作业车间调度问题。CHE等[19]使用混合整数规划模型来求解分时电价下单机调度问题,其目标是最小化电能成本。SHROUF等[20]在分时电价制度下,提出了离散时间整数规划模型和遗传算法求解具有断电机制的单机调度问题,其目标是最小化总电力成本。刘彩洁等[21]提出了改进NAGA-Ⅱ算法求解分时电价下柔性作业车间绿色调度问题,以最小化碳排放、能耗成本和最大完工时间为优化目标。另外,其他学者也研究了不同领域分时电价制度下的调度问题[22-23]。
目前,分时电价机制下对绿色车间调度问题的研究较少,同时考虑能耗成本和碳排放的RHFSP研究更鲜见。本文从节能降耗、绿色可持续发展的角度出发,提出了分时电价机制下同时考虑能耗成本和碳排放的可重入混合流水车间调度模型,在机器分配和工序排序的基础上,加入了工序的右移操作。针对该问题特点,提出一种改进的多目标文化基因算法(multi-objective memetic algorithm, MOMA),并通过数值实验将MOMA算法与另外3种算法进行了对比。
1 问题描述及数学模型
1.1 可重入混合流水车间调度问题
RHFSP可以描述为[24]:n个工件在s个工位上进行加工,在工位i中有mi台同速并行机,且至少有一个工位的并行机数量大于1,每个工件可以选择相应工位上的任何一台机器进行加工,并且有些工件需要访问某些工位多次,RHFSP示意图见图1。本文为每个工件分配机器,确定每台机器上加工工件的集合,计算每道工序的开始和结束时间,以最小化最大完工时间、总能耗成本和碳排放为目标进行优化求解。
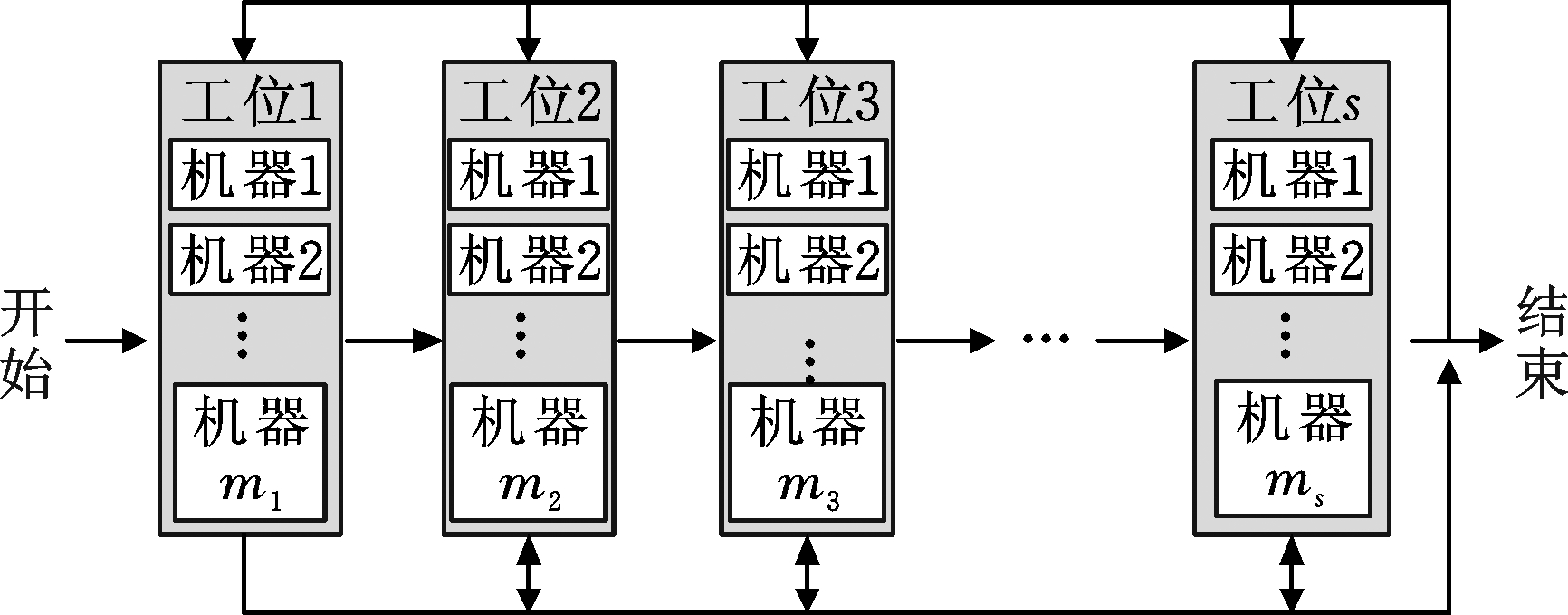
图1 可重入混合流水车间调度示意图
Fig.1 Diagram of re-entrant hybrid flow shop scheduling
假设在零时刻所有机器和工件都准备就绪;在任意时刻,每台机器至多加工一个工件,每个工件也只能被一台机器加工;每个工件的所有工序有先后约束,所有工件之间互不影响,工件之间的加工顺序没有先后约束;每个工件的可重入次数、工序的加工时间以及机器的单位能耗已知且恒定;工件一旦开始加工,不能被中断,不允许抢占;不考虑机器故障和机器的调整准备时间;任意两个连续加工阶段间的缓冲区容量不限。
1.2 数学模型
在文献[25-27]的研究基础上,本文提出了三目标RHFSP离散时间模型,该模型中包含大量的0-1变量,如果最小时间单位设置过小,会严重影响模型的计算速度,如果最小时间单位设置过大,误差将比较大,本文将最小时间单位设置为0.01 h。
目标函数:
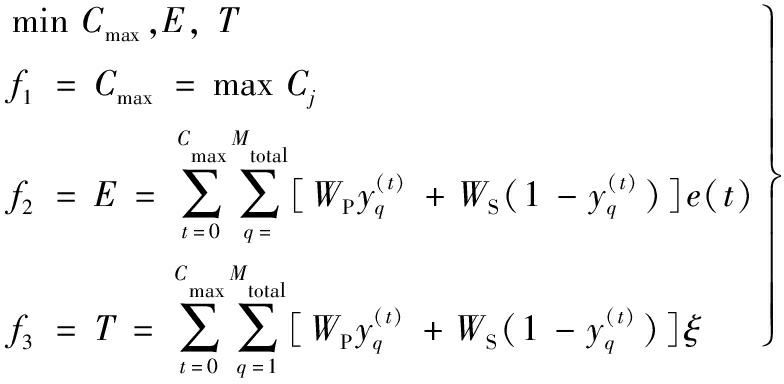
(1)
式中,Cmax为最大完工时间;Cj为工件j的完工时间,j为工件序号,j=1,2,…,n;E为总能耗成本,主要包括机器加工状态能耗成本和空转状态能耗成本;WP为机器加工状态单位时间能耗;WS为机器空转状态单位时间能耗;在加工时间t,如果机器q处于加工状态,![]() 反之,则
反之,则![]() 为分时电价函数;q为所有机器的编号,q=1,2,…,Mtotal,Mtotal=m1+m2+…+mi+…+ms,mi为工位i中的并行机器数,i为工位序号,i=1,2,…,s;T为碳排放;ξ为能耗与碳排放之间的转换系数,本文取ξ=0.272[28-29]。
为分时电价函数;q为所有机器的编号,q=1,2,…,Mtotal,Mtotal=m1+m2+…+mi+…+ms,mi为工位i中的并行机器数,i为工位序号,i=1,2,…,s;T为碳排放;ξ为能耗与碳排放之间的转换系数,本文取ξ=0.272[28-29]。
约束条件:
(2)
(3)
M(2-rijkl-rij′k′l)+M(1-Zjkj′k′)+
(Sj′k′-Sjk)≥Pjk
(4)
∀i,j<j′,l;Ojk∈Ui;Oj′k′∈Ui
M(2-rijkl-rij′k′l)+MZjkj′k′+(Sjk-Sj′k′)≥Pj′k′
(5)
∀i,j<j′,l;Ojk∈Ui;Oj′k′∈Ui
M(2-rijkl-rijk′l)+(Sjk′-Sjk)≥Pjk
(6)
∀i,k<k′,l;Ojk∈Ui;Ojk′∈Ui
Sjk≥0 Ejk=Sjk+Pjk ∀j,k
(7)
(8)
Cj≤Cmax ∀j
(9)
式中,rijkl为0-1变量,如果工序Ojk在工位i的第l台机器上加工,rijkl=1,反之,则rijkl=0;Sjk为工序Ojk的加工开始时间;Pjk为工序Ojk的加工时间;Ojk为工件j的第k道工序;k为工件j的工序序号,k=1,2,…,Nj;Nj为工件j的工序总数;l为工位i中的机器序号,l=1,2,…,mi;如果工件Ojk先于Oj′k′加工,Zjkj′k′=1,反之,则Zjkj′k′=0;M为一个足够大的正数;Cjk为工序Ojk的完工时间;Ui为在工位i中加工的所有工序的集合;Ejk为工序Ojk的加工结束时间。
式(1)为目标函数;约束式(2)确保工序Oj(k+1)的加工开始时间不早于Ojk工序的加工完成时间;约束式(3)保证每道工序只能在相应工位中的一台机器上加工;约束式(4)、式(5)和式(6)确保每台机器在同一时刻最多加工一道工序;约束式(7)规定工序Ojk的加工开始时间和完工时间;约束式(8)、式(9)描述了最大完工时间。
2 改进多目标文化基因算法
文化基因算法(MA)基于进化算法与局部搜索结合的技术框架,采用不同的搜索策略可以构成不同的文化基因算法。本文基于NSGA-Ⅱ改进多目标文化基因算法,根据编码规则设计了交叉算子和变异算子以及局部搜索算子,同时在保证最大完工时间不变的前提下加入了工序的右移操作,MOMA算法伪代码如下。
1. 初始化参数: 种群个数Pop_Size,交叉概率cr,变异概率mr,迭代次数Max_Gen等等
2. 随机生成初始种群POP0,计算所有个体的目标函数值,令g=0, 则POPg=POP0
3. while(g<Max_Gen)
4. 对种群POPg非支配排序,根据拥挤距离选择N个精英个体O0
5. if rand<cr
6. 种群POPg通过交叉操作生成子代O1
7. end
8. if rand<mr
9. 种群POPg通过变异操作生成子代O2
10. end
11. 将种群O1和O2合并为O3,计算所有个体的目标函数值
12. 对种群O3非支配排序,根据拥挤距离选择Pop_Size-N个较优个体O4
13. 将种群O0和O4合并为O5,对种群O5执行插入邻域和交换邻域两种局部搜索策略,右移操作,得到新的种群POPg+1
14. g←g+1
15. end while
16. 获取最优个体种群
2.1 编码和解码
文化基因算法主要用于求解连续函数的优化问题,很少用来处理离散类型的优化问题。本文采用随机键升序编码,构造从个体位置到工件排序的映射,然后按照文献[30]的方法进行解码,最后根据各种约束产生调度方案。
以一个6工件3工位的RHFSP为例,各工位的并行机器数量分别是3、2、2,假设所有机器加工状态单位时间能耗WP=8,机器空转状态单位时间能耗WS=1,各工件的所有工序加工时间见表1,分时电价函数(元/kW·h):
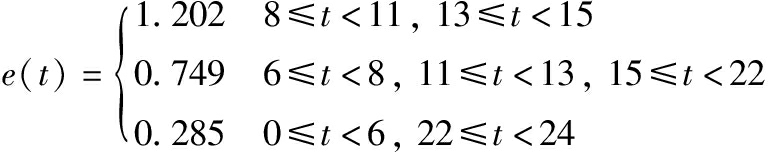
(10)
表1 6工件3工位的可重入调度问题示例
Tab.1 RHFSP example with 6 jobs and 3 stages h

加工时间(Pjk)首轮操作重入1重入2工位1工位2工位3工位1工位2工位3工位1工位2工位3工件1222022021工件2230222021工件3212020220工件4212201131工件5320210300工件6220122020
加工时间Pjk=0表示本轮该工件不在此工位上加工。由表1可知,所有工件均有两次重入,以工件1为例,它的加工顺序是工位1-2-3-2-3-2-3。采用随机键编码,个体长度等于工件总数,各元素在[0, 1]内任意取值,通过对各位置元素进行升序排列得到对应的工件排序。通过解码过程为每道工序在每个工位选取一台合适的机器,并确定每台机器上需要加工的所有工序的先后顺序及其开始加工时间和结束时间,最后求得目标函数值,解码的详细过程如下。
(1)从染色体中选择第一个基因i(即工件i),将工件i的所有工序安排在能够最早完成它的机器上,并记录每道工序的开始加工时间和完工时间。
(2)选择下一个基因i′并为其安排机器。假设为工序Oi′j安排机器,首先获取工序Oi′j可用的机器集合MS。
(3)从MS选择机器q,获取机器q所有的空闲时间段[MStart,MEnd],遍历机器q所有空闲时间段,工序Oi′j的最早开始加工时间ti′j如下所示:
tij=max(Ci′j-1,MStart)
(4)Oi′j寻找合适的插入点:
ti′j+Pi′j≤MEnd
如果没有找到满足条件的空闲时间段,则将工序Oi′j的开始加工时间设置为ti′j=MLq,其中MLq表示机器q最后一道工序的完工时间。
(5)遍历MS中所有机器,重复步骤(3)、步骤(4),选择最小的ti′j。
(6)计算工序Oi′j的加工完成时间:
Ci′j=ti′j+Pi′j
(7)重复步骤(2)~(6)至染色体中所有的基因处理完毕。
以个体(0.814 7, 0.913 4, 0.632 4, 0.127 0, 0.097 5, 0.905 8)为例,依照升序排列其对应的工件排序为5-4-3-1-6-2,将该排序解码成一个可行调度方案,所得到的甘特图见图2和图3。该调度方案求得的目标函数值f1=25 h、f2=417.285 5元和f3=168.912 0 kg。
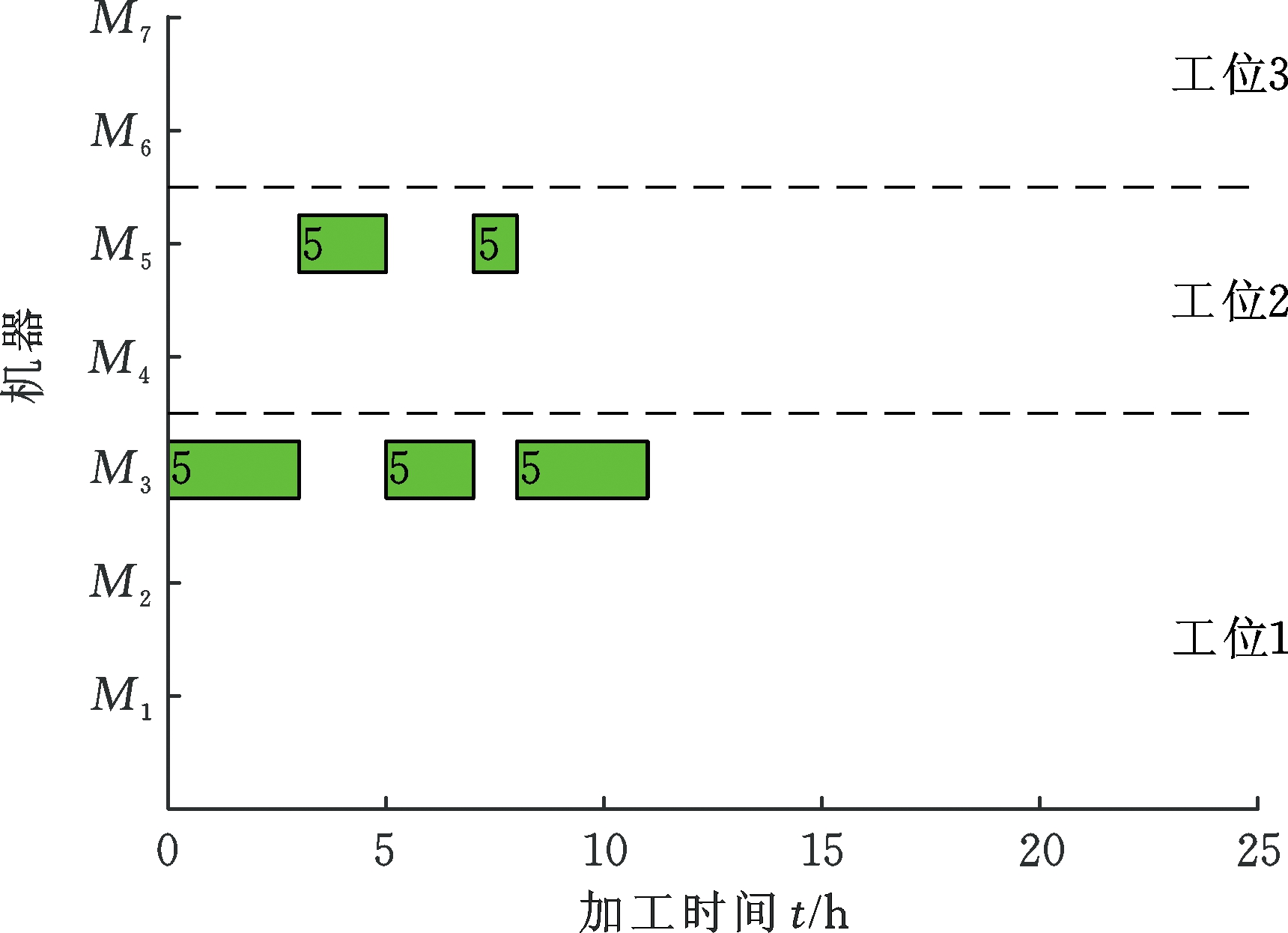
图2 工件5的调度方案
Fig.2 Scheduling job 5
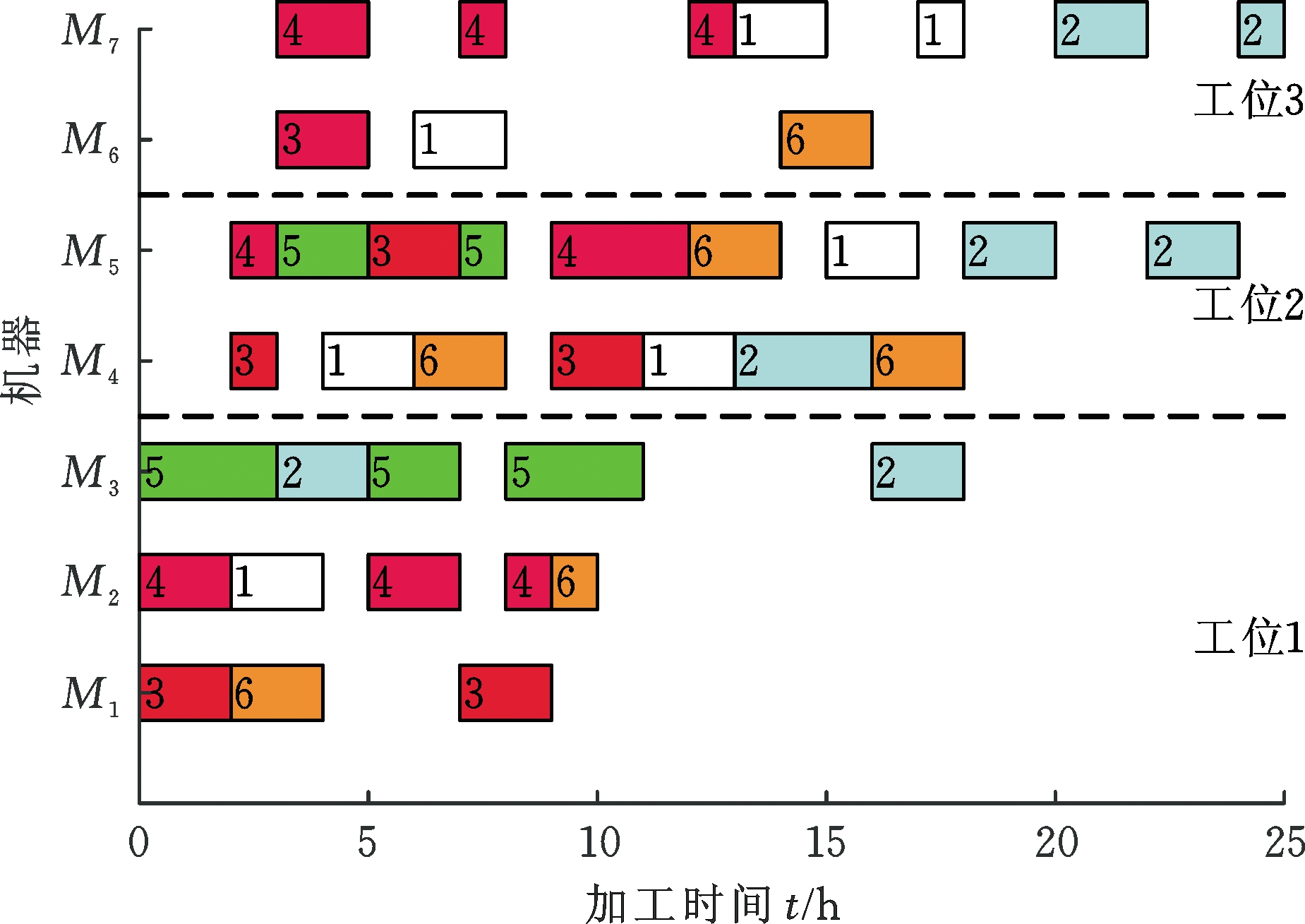
图3 所有工件的调度方案
Fig.3 Scheduling all jobs
2.2 交叉算子
交叉算子有助于将优良个体的染色体片段遗传给后代,同时交叉算子一般起全局搜索的作用,可以开采未知的空间,本文采用优先工序交叉(precedence operation crossover,POX)。如图4所示,POX交叉过程如下:①随机选择两个父代染色体P1和P2,将所有工件分到两个非空子集C1和C2中;②将P1中属于C1的工件复制到O1,将P2中属于C1的工件复制到O2,并保持位置不变;③将P1中属于C2的工件复制到O2,将P2中属于C2的工件复制到O1,并保持顺序不变;④O1和O2为交叉后得到的子代。
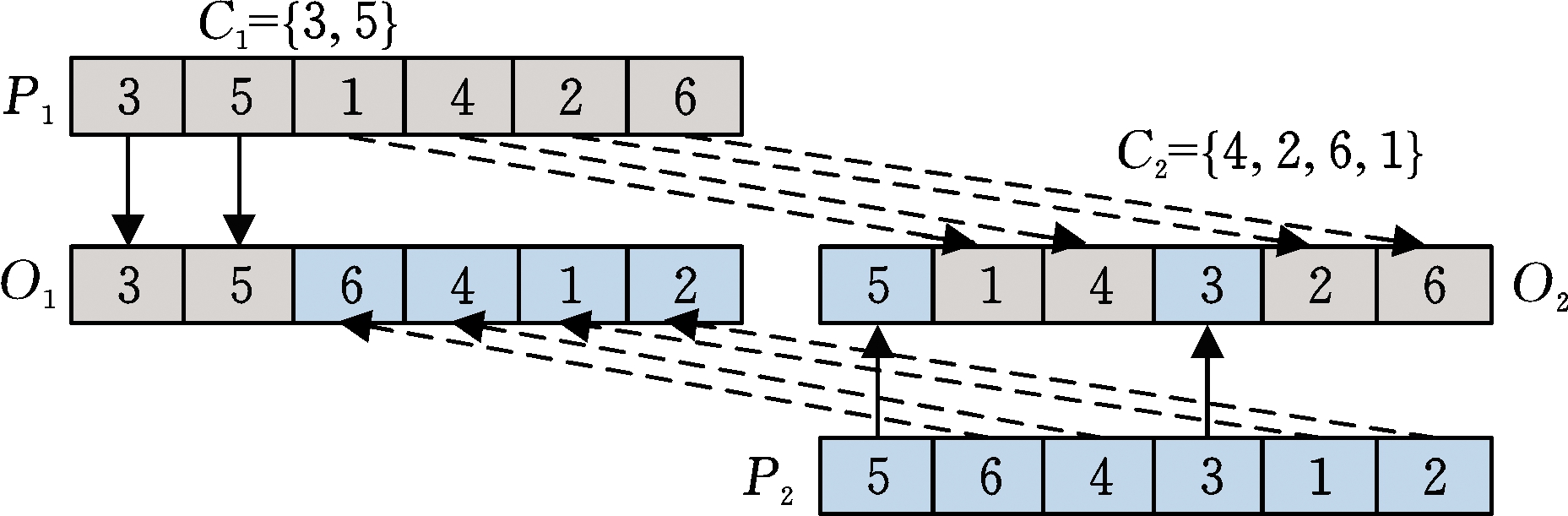
图4 POX交叉示意图
Fig.4 Diagram of POX crossover

图5 局部最优变异示意图
Fig.5 Diagram of local optimal mutation
2.3 变异算子
传统的变异策略随机性较强,当达到较高代数后,通过该方法基本得到的都是坏解,因此,本文采取一种局部最优的变异策略。如图5所示,在P1中随机选择3个基因{3,1,4}作为一个局部π,将π中基因所有的排列组合列出,分别为{3,4,1},{4,3,1},{4,1,3},{1,3,4},{1,4,3},然后对每一种可能性组合进行评估,最终根据支配关系选择结果最好的替换掉{3,1,4},假设{1,3,4}评估结果最好,则变异后子代染色体O1为{1,5,3,4,2,6}。
2.4 局部搜索算子
本文采用插入邻域和交换邻域两种结构来提高算法的局部搜索性能和种群多样性。
(1)插入邻域。首先,从个体中随机删除一个工件j,得到具有n-1个工件的序列π;然后,将工件j插入π的n个空隙中,分别计算工件j插入后所得n个新个体的目标函数值fitness(i),i∈[1,n];最后,判断其支配关系,令最优解best=fitness(1)。若fitness(i)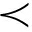 best,则best=fitness(i)。依此类推,取best所对应的序列作为最优插入序列并记录其目标函数值。
best,则best=fitness(i)。依此类推,取best所对应的序列作为最优插入序列并记录其目标函数值。
(2)交换邻域。首先,从个体中随机选择一个工件j,分别将工件j和剩余的n-1工件交换位置;然后,计算交换后的目标函数值fitness(i),i∈[1,n-1],同时令原序列对应的目标函数值为fitness(n);最后,判断其支配关系,令最优解best=fitness(1),若fitness(i)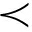 best,则best=fitness(i),依此类推,取best所对应的序列作为最优交换序列并记录其目标函数值。
best,则best=fitness(i),依此类推,取best所对应的序列作为最优交换序列并记录其目标函数值。
2.5 右移操作
分时电价制度下考虑能耗成本和碳排放的可重入混合流水车间调度,不仅要为工件选择合适的机器,还要合理地确定每道工序的开始加工时间。由于RHFSP不可避免地会出现机器和工件等待的情形,特别是在工件规模较大的情况下,因此可以充分利用这些等待时间来调整工序的加工时段。在解码过程中加入右移操作,根据Pareto支配关系,从工序可能的开始加工时间中选择使该工序能耗和碳排放最小的时间作为调整后的工序开始加工时间。如果符合条件的开始时间有多个,则选择值最大的作为开始加工时间,以保证工序有足够的右移空间。由于解码方法的限制,每个工序按最早开始时间解码,因此所有工序没有左移的空间,只能向右移动。从调整原理可以看出,后一个工序时段的调整会影响到前一个工序时段的调整,所以右移操作应遵循从后向前的规则依次进行。首先将所有工序按照完工时间非增排列,然后按此顺序依次进行右移操作,以工序Ojk为例,详细调整过程如下:
假设工序Ojk在Mil上加工,Sjk调整区间为t∈[tmin,tmax],在不影响生产效率的前提下,工件j可以选择此范围内的任意时间作为开始加工时间,tmin=Sjk,tmax=min(Sj′k′,Sj(k+1))-Pjk,如果存在多个符合条件的t,则取最大的t。
(1)如果Sj′k′≤Sj(k+1),相应的调整区间如图6所示,此时tmax=Sj′k′-Pjk,即向右移动后工序Ojk完工时间不能大于同一机器上下一道工序的开始加工时间Sj′k′。

图6 当Sj′k′≤Sj(k+1)时调整示意图
Fig.6 Diagram of adjustment when Sj′k′≤Sj(k+1)
(2)如果Sj′k′>Sj(k+1),相应的调整区间如图7所示,此时tmax=Sj(k+1)-Pjk,即向右移动后工序Ojk完工时间不能大于该工件下一道工序的开始加工时间Sj(k+1)。
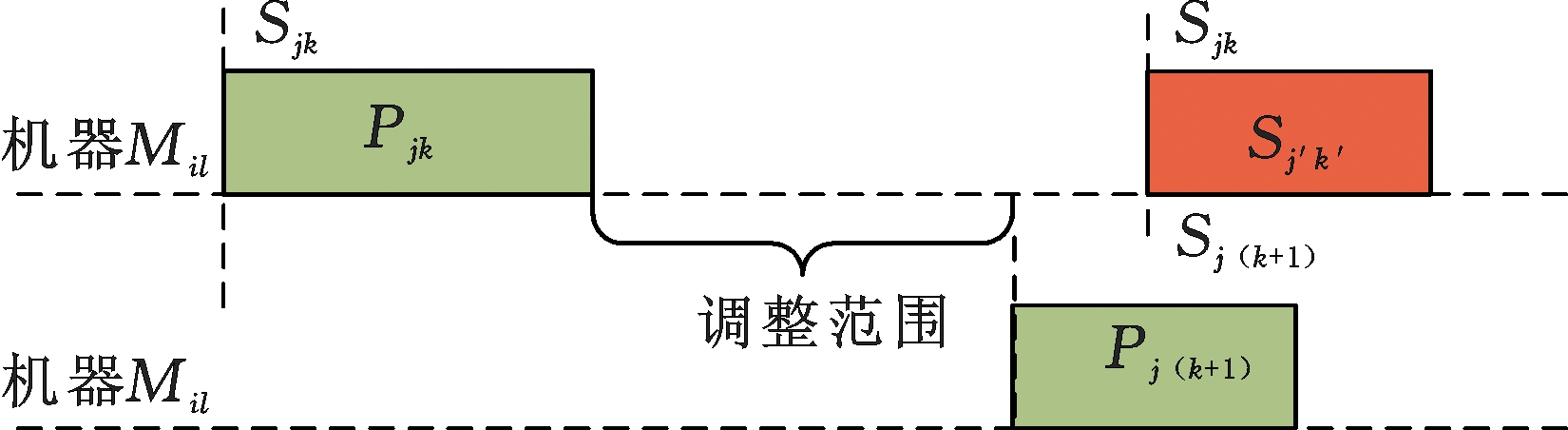
图7 当Sj′k′>Sj(k+1)时调整示意图
Fig.7 Diagram of adjustment when Sj′k′>Sj(k+1)
右移操作的伪代码如下:
1. 获取工序Ojk开始加工时间范围tmin=Sjk,tmax=min{Sj′k′,Sjk+1}-Pjk
2. 当Start=tmin时,初始化二个目标函数值goodResults=[E,T]
3. 划分时间粒度为1%小时,可能开始时间有![]() 个
个
4. for i=1:(tmax-tmin)/0.01
5. 当Start=tmin+0.01*i时,计算目标函数值E和T
6. if[E,T] goodResults//判断支配关系
goodResults//判断支配关系
7. goodResults=[E,T]
8. goodstart=Start
9. end
10. end
11. 经过右移操作后,工序Ojk最佳开始时间为goodstart
(3)右移操作以后,不可避免地会出现某些工序能够转移到同工位其他机器上加工的情况,而且这种转移在不影响最大完工时间的前提下,可以使机器尽早处于停机状态,减少空转能耗。若Oj″k″为机器Mil′的最后一道工序,同时满足Sj″k″≥Ejk且Sj′k′≥Ej″k″,转移后Oj″k″的开始加工时间和完工时间保持不变,但是调整后Oj″k″由机器Mil来加工,局部调整示意图见图8。
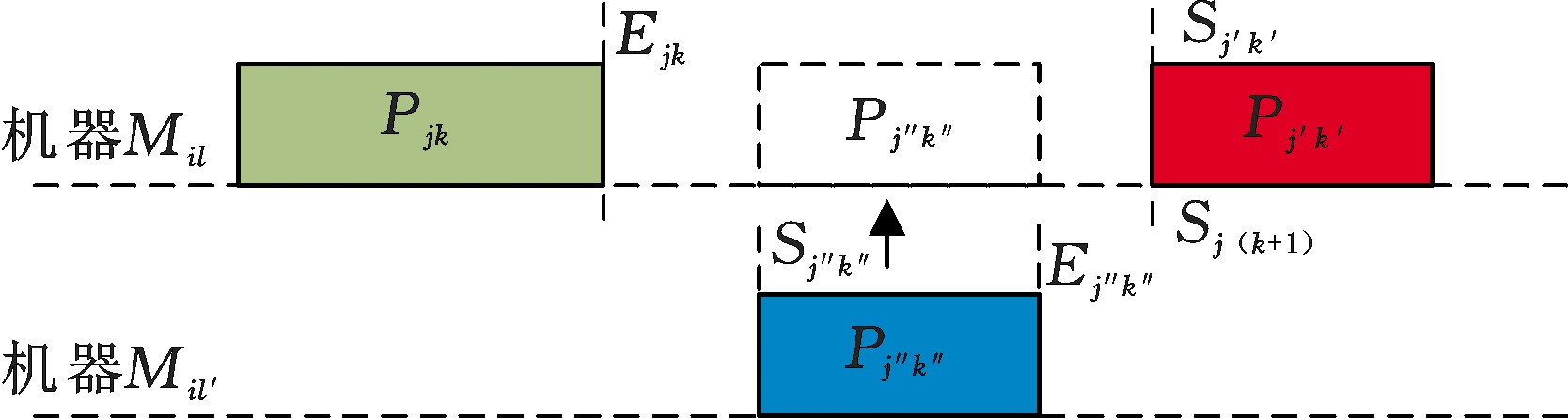
图8 局部调整示意图
Fig.8 Diagram of partial adjustment

图9 右移操作后甘特图
Fig.9 Gantt charts after right-shift procedure
以表1中的数据为例,图3所示的调度方案加入右移操作后,所得甘特图见图9。由图3可知,工件5在机器3上的第3道工序加工时间段为8~11 h,并且在时间段11~16 h区间内机器3处于空转状态,此时该道工序的加工能耗成本为28.829 8元,碳排放为6.528 kg。由图9可知,按照从右向左的顺序,工件5在机器3上的第3道工序的开始加工时间可在8~13 h之间取值,经计算加工时间段为10~13 h效果最好,此时该道工序加能耗成本为21.600 0元,碳排放为6.528 kg,对比可知,右移操作效果明显。同时,根据右移规则,工件3在机器1上的第2道工序转移到机器3上,工件6在机器2上的第一道工序转移到机器3上,导致机器1和机器2提前结束加工,减少了机器的空转时间,最终3个目标函数为f1=25 h、f2=406.482 8元和f3=167.280 0 kg。对比可知,在保证f1不变的前提下,f2和f3均有所减少(Δf2=10.802 7元,Δf3=1.632 0 kg),验证了右移操作的有效性。
3 数值实验
将MOMA算法与多目标蚁狮优化算法(multi-objective ant lion optimization algorithm,MOALO)、多目标粒子群优化算法(multi-objective particle swarm optimiazation algothrim,MOPSO)和带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA-Ⅱ)3种多目标优化算法进行对比研究。数值实验环境为操作系统Windows 10,处理器Intel Corei7-4770MCPU@3.40GHz,内存16G,采用MATLAB R2017a实现算法编程。为了客观地比较算法的性能,将各种算法中共有的参数取相同值。
3.1 实验数据描述
本文选取文献[30]中的测试问题作为算例,该测试集共包含120个小规模测试问题和120个大规模测试问题。本文分别从小规模问题和大规模问题中随机选择4个用于测试。问题规模用“重入次数*工位数*工件数”来表示,例如“2*10*20”表示2次重入、10个工位和20个工件数的案例。本实验采用三时段分时电价函数,周期为24 h,函数表达式见式(10),分时电价图见图10,峰时段的电价为1.202元/(kW·h),谷时段电价为0.285元/(kW·h),峰时段电价约为谷时段电价的4.2倍,因此制造企业有巨大的空间通过加工时段的转移来降低总能耗成本。
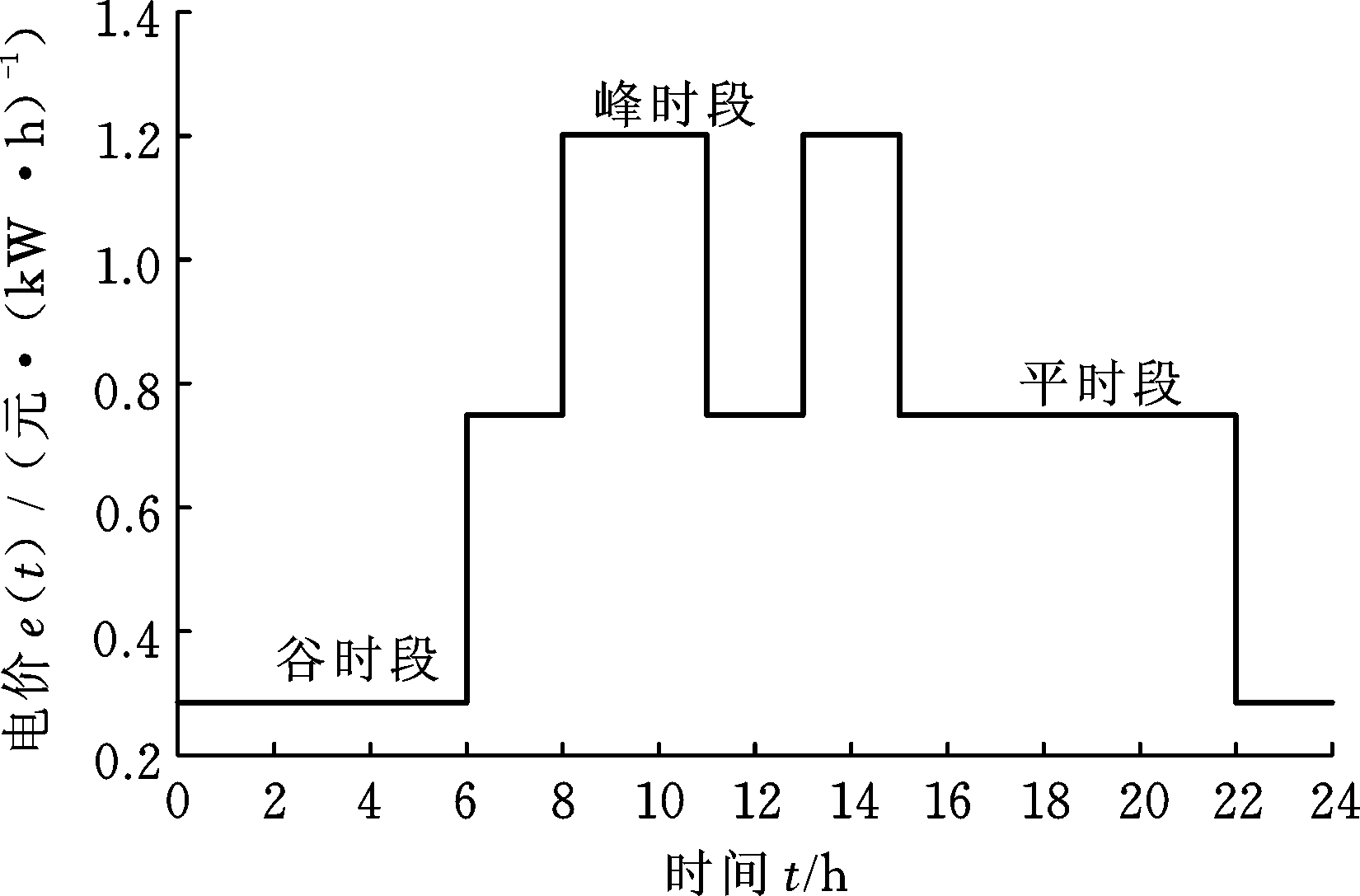
图10 24 h分时电价图
Fig.10 TOU electricity tariffs over 24-hour period
3.2 算法性能评价指标
本文选取了3个性能评价指标:反世代距离(inverted generational distance, IGD)、支配性指标Ω和分布性能指标Δ。由于所测试问题的真实最优Pareto前沿未知,本文将4种算法所得非支配解并集中的非支配解作为最优Pareto前沿。同时,由于3个优化目标的度量单位不同,因此需要对目标函数值进行归一化处理后再参与3个性能评价指标的计算。
IGD是通过计算最优Pareto前沿上的每个点到某种算法获取的Pareto前沿之间的最小距离和来评价算法的收敛性和非劣解的多样性,它是一个综合性能评价指标。计算公式如下:
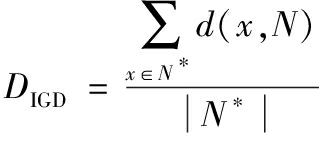
(11)
其中,|N*|为最优Pareto前沿中非劣解的个数;N为算法获取的Pareto非劣解集;d(x,N)为N*中个体x到种群N的最小欧氏距离。IGD值越小,算法的收敛性和非劣解的多样性越好。
支配性指标Ω表示某一算法获得非劣解同时为最优Pareto前沿上非劣解的百分比,其中“∪”为并集运算符,“\”为余集运算符。计算公式如下:
其中,|P(A)|为集合A中非劣解的个数,Ha为第a种算法获得的非劣解集。Ω取值越大,对应算法的非支配解集的支配性能越好,Ω∈[0,1]。
指标Δ用来衡量Pareto前沿上非劣解的分布性能,计算公式如下:
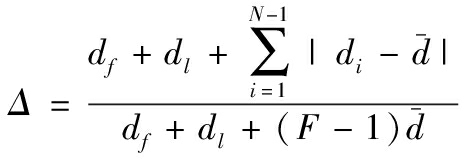
其中,F为Pareto前沿中非劣解个数;df和dl为Pareto前沿上的两个边界解与最优Pareto前沿上的两个极端解之间的欧氏距离;di为Pareto前沿上第i与i+1个相邻解间的欧氏距离;![]() 为di的平均值。Δ取值越小,非劣解分布的均匀性和宽广性越好。
为di的平均值。Δ取值越小,非劣解分布的均匀性和宽广性越好。
3.3 实验结果及分析
针对每个算例,每种算法独立运行20次,每运行一次得到一组IGD、Ω、Δ值。表2统计了4种算法20次运行后各个评价指标的最小值(min)和均值(avg),粗体字表示每个案例所对应指标的最优结果。
最小值和均值只能从宏观上呈现各个算法的求解效果,通过相关样本的Wilcoxon符号秩检验能够得出两两算法之间是否具有显著差异。针对所有测试问题的3个评价指标,分别将MOMA与其他3种算法进行两两比较,p=1表示显著水平为0.05时是显著的。从表2和表3可以看出,在所有测试问题上,就IGD和Ω指标而言,MOMA和其他3种算法均具有显著性差异并且效果最优,因此在95%的置信水平下,所提出的MOMA算法比其他算法具有显著的优越性;就Δ指标而言,四者无显著性差别。
表2 8个测试问题的四种算法结果对比
Tab.2 Comparisons of four algorithms for the eight test problems
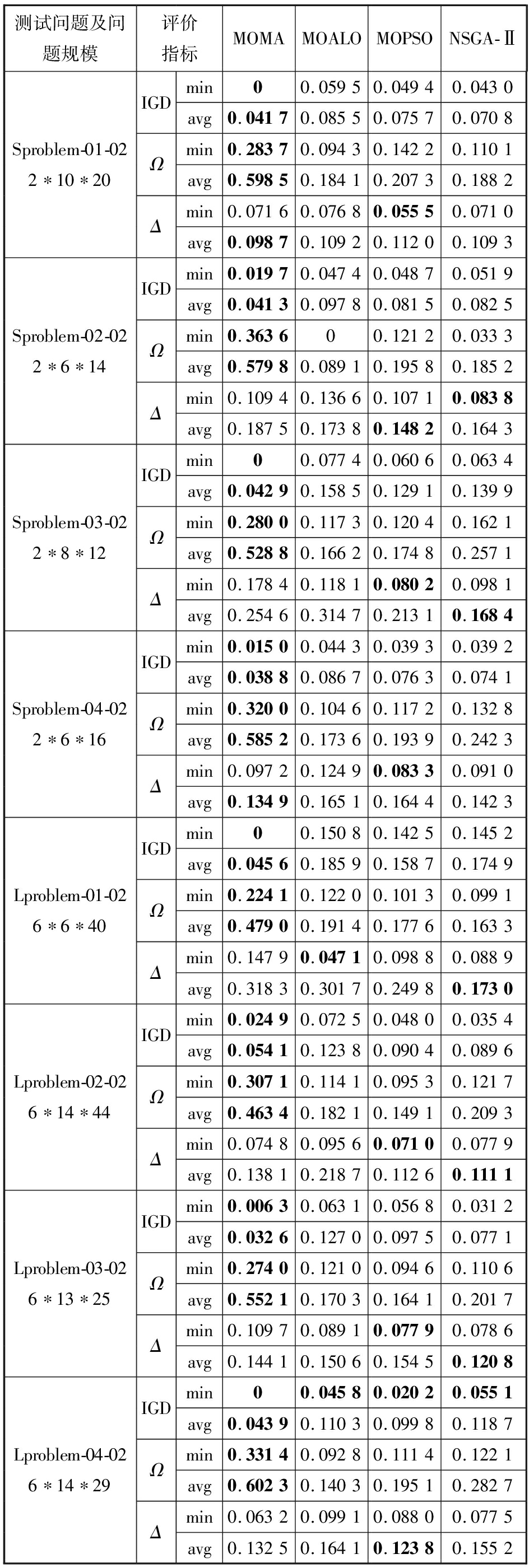
测试问题及问题规模评价指标MOMAMOALOMOPSONSGA-ⅡSproblem-01-022∗10∗20IGDΩΔmin00.05950.04940.0430avg0.04170.08550.07570.0708min0.28370.09430.14220.1101avg0.59850.18410.20730.1882min0.07160.07680.05550.0710avg0.09870.10920.11200.1093Sproblem-02-022∗6∗14IGDΩΔmin0.01970.04740.04870.0519avg0.04130.09780.08150.0825min0.363600.12120.0333avg0.57980.08910.19580.1852min0.10940.13660.10710.0838avg0.18750.17380.14820.1643Sproblem-03-022∗8∗12IGDΩΔmin00.07740.06060.0634avg0.04290.15850.12910.1399min0.28000.11730.12040.1621avg0.52880.16620.17480.2571min0.17840.11810.08020.0981avg0.25460.31470.21310.1684Sproblem-04-022∗6∗16IGDΩΔmin0.01500.04430.03930.0392avg0.03880.08670.07630.0741min0.32000.10460.11720.1328avg0.58520.17360.19390.2423min0.09720.12490.08330.0910avg0.13490.16510.16440.1423Lproblem-01-026∗6∗40IGDΩΔmin00.15080.14250.1452avg0.04560.18590.15870.1749min0.22410.12200.10130.0991avg0.47900.19140.17760.1633min0.14790.04710.09880.0889avg0.31830.30170.24980.1730Lproblem-02-026∗14∗44IGDΩΔmin0.02490.07250.04800.0354avg0.05410.12380.09040.0896min0.30710.11410.09530.1217avg0.46340.18210.14910.2093min0.07480.09560.07100.0779avg0.13810.21870.11260.1111Lproblem-03-026∗13∗25IGDΩΔmin0.00630.06310.05680.0312avg0.03260.12700.09750.0771min0.27400.12100.09460.1106avg0.55210.17030.16410.2017min0.10970.08910.07790.0786avg0.14410.15060.15450.1208Lproblem-04-026∗14∗29IGDΩΔmin00.04580.02020.0551avg0.04390.11030.09980.1187min0.33140.09280.11140.1221avg0.60230.14030.19510.2827min0.06320.09910.08800.0775avg0.13250.16410.12380.1552
表3 MOMA算法与其他算法Wilcoxon符号秩检验
Tab.3 Wilcoxon signed rank test of MOMA and other algorithms
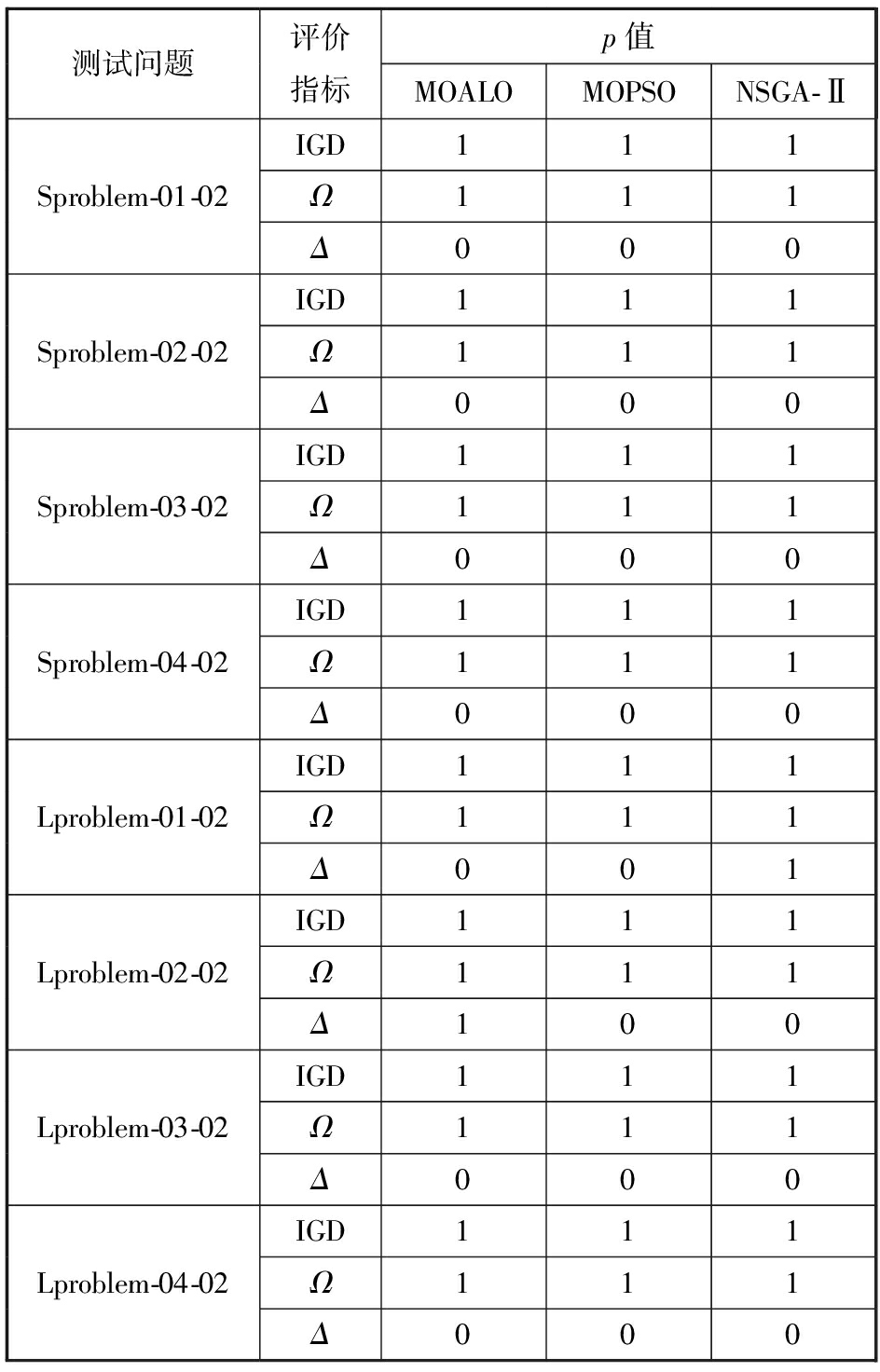
测试问题评价指标p值MOALOMOPSONSGA-ⅡSproblem-01-02IGD111Ω111Δ000Sproblem-02-02IGD111Ω111Δ000Sproblem-03-02IGD111Ω111Δ000Sproblem-04-02IGD111Ω111Δ000Lproblem-01-02IGD111Ω111Δ001Lproblem-02-02IGD111Ω111Δ100Lproblem-03-02IGD111Ω111Δ000Lproblem-04-02IGD111Ω111Δ000
下面以Sproblem-02-02为例来分析右移操作对调度结果的影响。该算例共有14个工件,10台机器,6个工位,每个工位上的并行机器数量分别是2、1、2、2、2、1,所有工件可重入2次。4种算法的Pareto前沿如图11所示,观察可知,采用MOMA算法所得的解大都可以支配其他算法所得解,同时从3个目标函数的两两比较可以看出,MOMA算法所得的解大部分集中在坐标系的左下方,因此MOMA算法求解效果最好。
以MOMA的一个非支配解(f1=104 h,f2=2 848.120 5元和f3=1 173.408 0 kg)所对应的加工顺序14-9-4-13-6-7-8-5-3-1-10-11-2-12为例,图12为分时电价下带有右移操作的甘特图,图13为分时电价下无右移操作的甘特图(f1=104 h, f2=2 959.585 9元和f3=1 178.848 0 kg)。对比可知,有很多工序的加工时段发生了转移,如机器1上的工件10,机器6上的工件12和5等都发生了转移,在保证生产效率不变的前提下,能耗成本降低3.76%,共111.465 4元,碳排放降低0.46%,共5.44 kg。
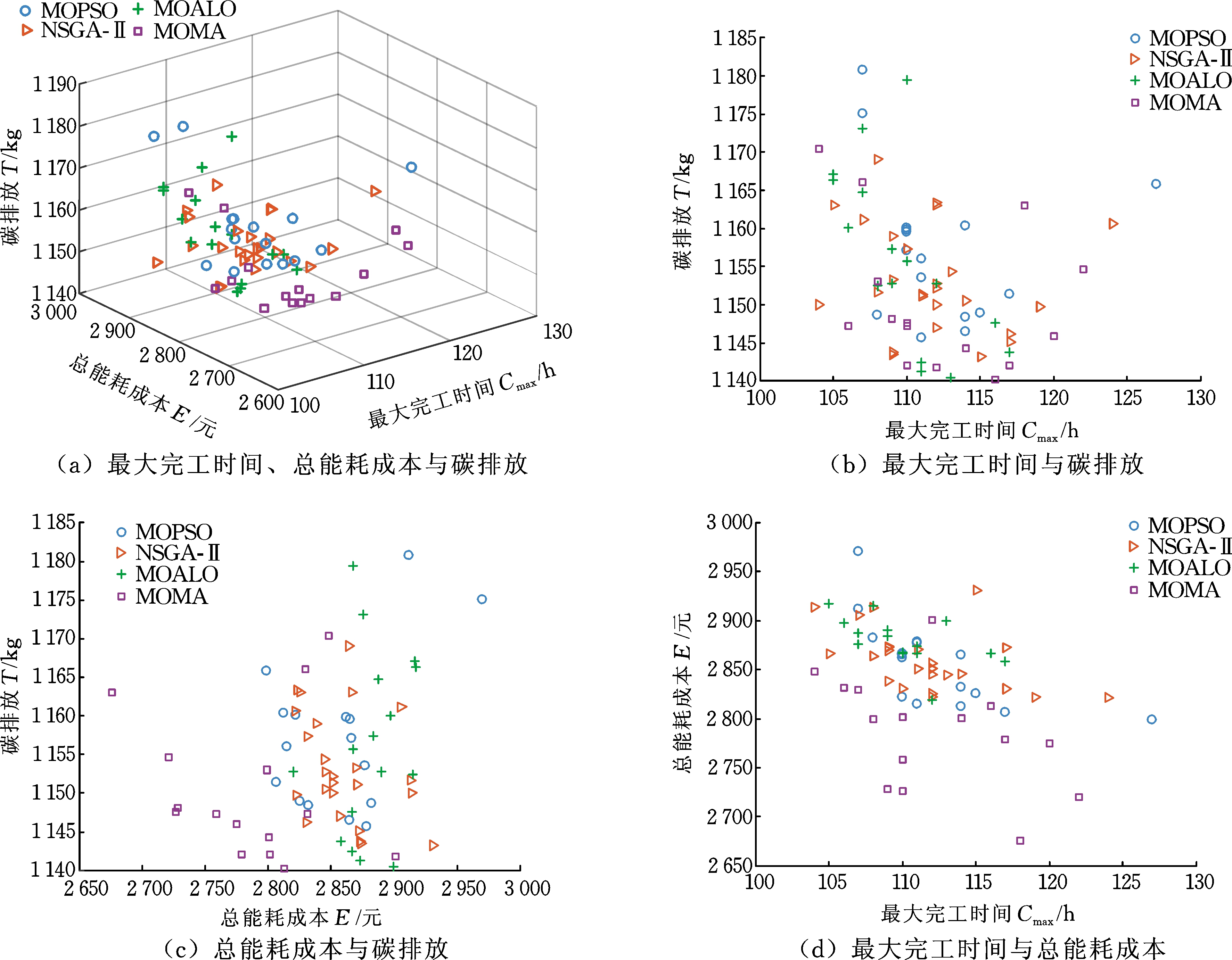
图11 Sproblem-02-02案例4种算法Pareto前沿
Fig.11 Pareto front of 4 algorithms about Sproblem-02-02
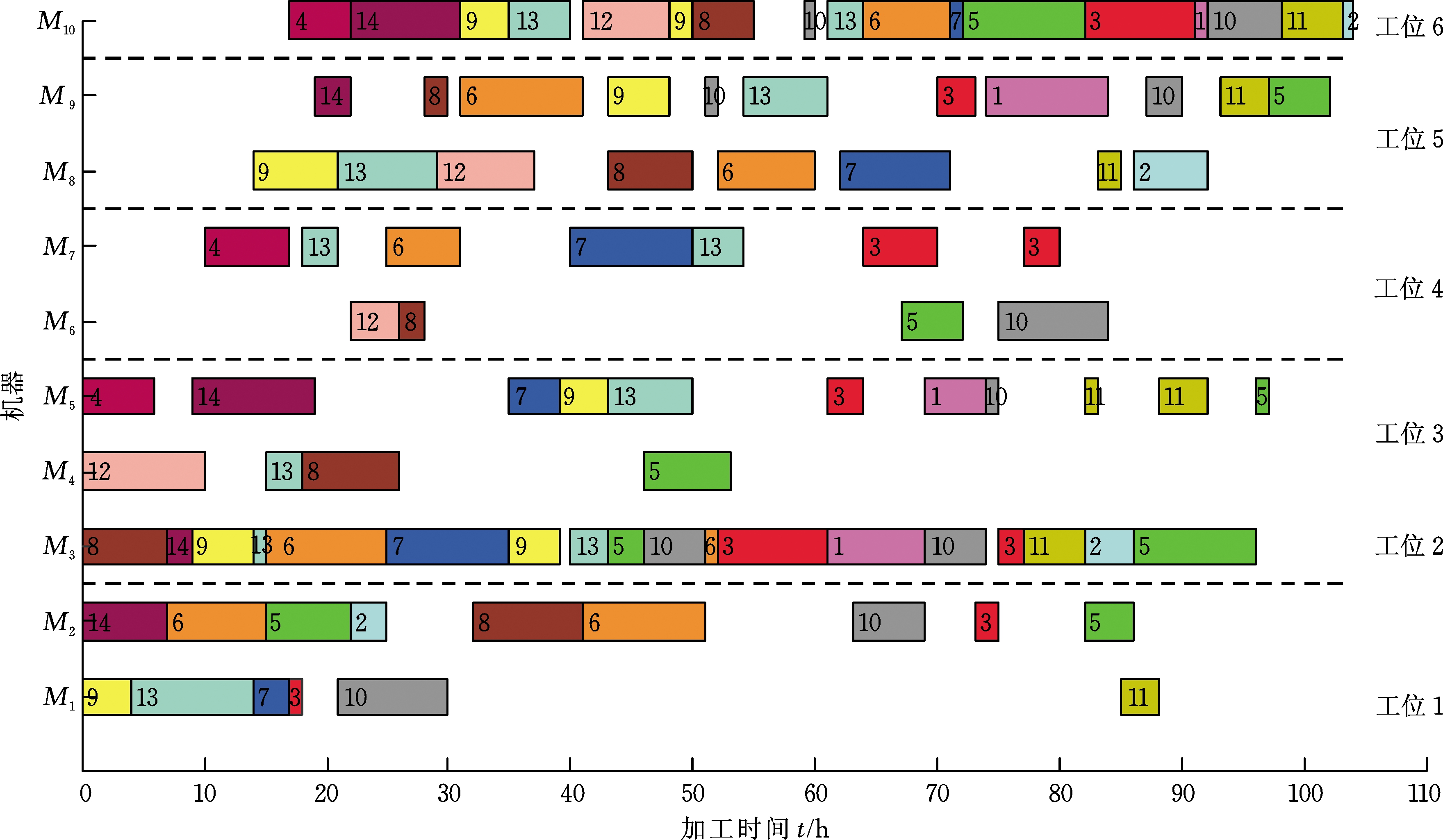
图12 分时电价下带有右移操作的甘特图
Fig.12 Gantt charts with right-shift procedure under TOU electricity tariffs
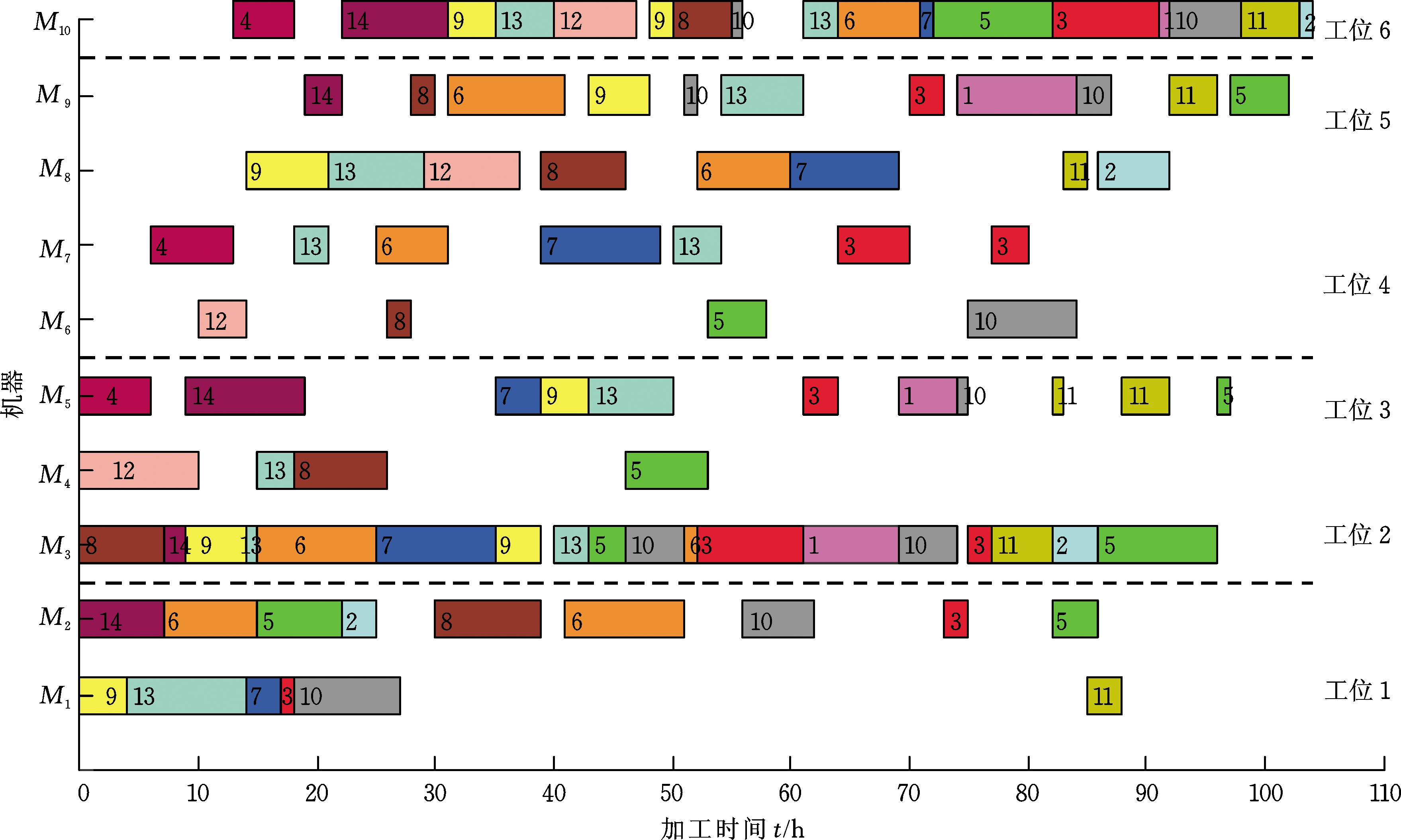
图13 分时电价下无右移操作的甘特图
Fig.13 Gantt charts without right-shift procedure under TOU electricity tariffs
在加工周期内,所有机器的总耗能趋势图见图14,其中EC表示所有机器的总能耗。由图14可知,在20 h和60 h附近属于高电价时段,通过右移操作后所有机器用电总负荷有所下降,而在25 h和50 h附近为低电价时段,通过右移动操作后所有机器用电总负荷有所增加,因此分时电价下用电负荷发生了较为明显的转移,达到了“削峰填谷”的目的,有效降低了能耗成本和碳排放。
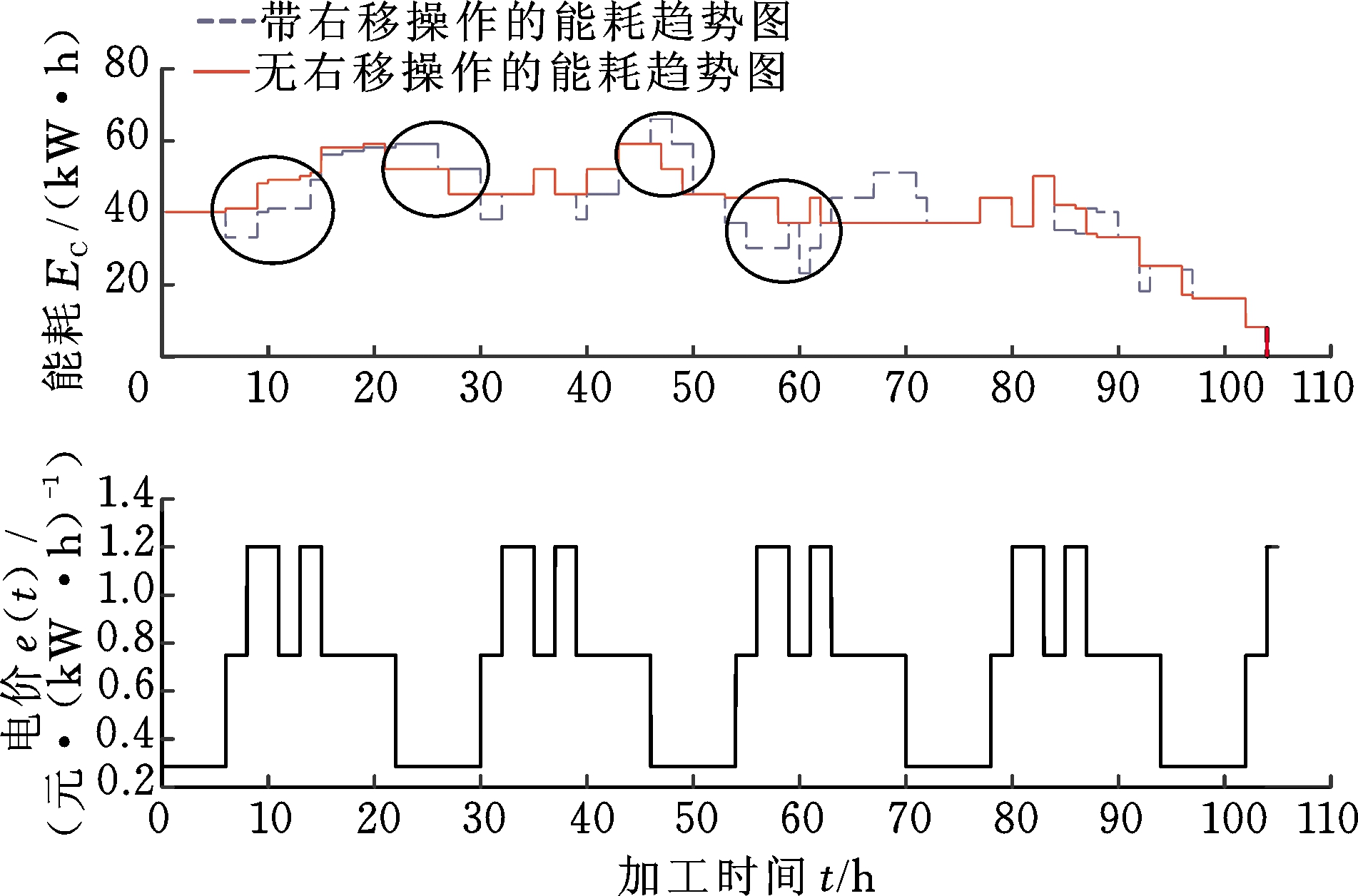
图14 加工周期内机器总能耗趋势图
Fig.14 Trend chart of total energy consumption of all machines in the processing cycle
综上所述,分时电价制度下考虑能耗成本和碳排放的RHFSP能够在保证生产效率不变的前提下,降低机器的能耗成本,减少碳排放,提高企业竞争力,协调经济效益和社会效益,实现经济的绿色可持续发展。
4 结论
本文基于机器加工和空转两种工作状态的能耗特点,建立了以最小化最大完工时间、总能耗成本和碳排放为目标的可重入混合流水车间调度优化模型。针对所求解问题的特点,提出了一种改进的多目标文化基因算法,通过编码和解码、交叉和变异算子、局部搜索算子和右移操作等来提升算法的寻优能力。采用不同规模的算例验证了改进算法的有效性和优越性。实验结果表明,MOMA算法能够有效地求解分时电价机制下考虑能耗和碳排放的可重入混合流水车间调度问题。
在实际情况中,不同的发电方式下能耗与碳排放之间的转换系数是有差异的,本文的局限性在于没有考虑这种差异,认为能耗与碳排放之间的转换系数为常数ξ,在这种情况下碳排放量仅与机器空转能耗有关。今后,我们将进一步研究考虑绿色指标的可重入混合流水车间调度问题,对本文的模型进行相应调整,例如涉及不相关并行机,考虑开关机的策略,考虑生产调度与设备维护的联合优化,以及在不同发电方式下考虑分时电价机制的调度优化等。
[1] WANG M Y, SETHI S P, van de VELDE S L.Minimizing Makespan in a Class of Reentrant Shops[J].Operations Research, 1997, 45(5):702-712.
[2] GRAVES S C, MEAL H C, STEFEK D, et al.Scheduling of Re-entrant Flow Shops[J].Journal of Operations Management, 1983, 3(4):197-207.
[3] CHEN J S, PAN J C H, WU C K.Minimizing Makespan in Reentrant Flow-shops Using Hybrid Tabu Search[J].The International Journal of Advanced Manufacturing Technology, 2007, 34(3):353-361.
[4] KIM H W, LEE D H.Heuristic Algorithms for Re-entrant Hybrid Flow Shop Scheduling with Unrelated Parallel Machines[J].Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2009, 223(4):433-442.
[5] EL-KHOULY I A, EL-KILANY K S, EL-SAYED A E.Modelling and Simulation of Re-entrant Flow Shop Scheduling:an Application in Semiconductor Manufacturing[C]//2009 International Conference on Computers & Industrial Engineering.Troyes, 2009:211-216.
[6] HEKMATFAR M, FATEMI GHOMI S M T, KARIMI B.Two Stage Reentrant Hybrid Flow Shop with Setup Times and the Criterion of Minimizing Makespan[J].Applied Soft Computing, 2011, 11(8):4530-4539.
[7] SHEN J, WANG L, ZHENG H.A Modified Teaching-learning-based Optimization Algorithm for Bi-objective Re-entrant Hybrid Flowshop Scheduling[J].International Journal of Production Research, 2016, 54(12):3622-3639.
[8] SHEN J, WANG L, DENG J, et al.A Pareto-based Discrete Harmony Search Algorithm for Bi-objective Reentrant Hybrid Flowshop Scheduling Problem[M]//KIM J H, GEEM Z W.Harmony Search Algorithm.Berlin:Springer, 2016:435-445.
[9] FANG K, UHAN N, ZHAO F, et al.A New Approach to Scheduling in Manufacturing for Power Consumption and Carbon Footprint Reduction[J].Journal of Manufacturing Systems, 2011, 30(4):234-240.
[10] LU C, GAO L, LI X, et al.Energy-efficient Permutation Flow Shop Scheduling Problem Using a Hybrid Multi-objective Backtracking Search Algorithm[J].Journal of Cleaner Production, 2017, 144:228-238.
[11] 王凌, 王晶晶, 吴楚格.绿色车间调度优化研究进展[J].控制与决策, 2018, 33(3):385-391.
WANG Ling, WANG Jingjing, WU Chuge.Advances in Green Shop Scheduling and Optimization[J].Control and Decision, 2018, 33(3):385-391.
[12] DING J Y, SONG S, WU C.Carbon-efficient Scheduling of Flow Shops by Multi-objective Optimization[J].European Journal of Operational Research, 2016, 248(3):758-771.
[13] 艾子义, 雷德明.基于新型邻域搜索以碳排放为目标的混合流水车间低碳调度[J].信息与控制, 2017, 46(3):311-317.
AI Ziyi, LEI Deming.Novel Neighborhood Search for Low Carbon Scheduling of Hybrid Flow Shop with Carbon Emission[J].Information and Control, 2017, 46(3):311-317.
[14] PIROOZFARD H, WONG K Y, WONG W P.Minimizing Total Carbon Footprint and Total Late Work Criterion in Flexible Job Shop Scheduling by Using an Improved Multi-objective Genetic Algorithm[J].Resources, Conservation and Recycling, 2018, 128:267-283.
[15] PIROOZFARD H, WONG K Y, TIARA M K.Reduction of Carbon Emission and Total Late Work Criterion in Job Shop Scheduling by Applying a Multi-objective Imperialist Competitive Algorithm[J].International Journal of Computational Intelligence Systems, 2018, 11(1):805-829.
[16] LUO H, DU B, HUANG G Q, et al.Hybrid Flow Shop Scheduling Considering Machine Electricity Consumption Cost[J].International Journal of Production Economics, 2013, 146(2):423-439.
[17] WANG Y, LI L.Time-of-use Based Electricity Demand Response for Sustainable Manufacturing Systems[J].Energy, 2013, 63:233-244.
[18] MOON J Y, PARK J.Smart Production Scheduling with Time-dependent and Machine-dependent Electricity Cost by Considering Distributed Energy Resources and Energy Storage[J].International Journal of Production Research, 2014, 52(13):3922-3939.
[19] CHE A, ZENG Y, LYU K.An Efficient Greedy Insertion Heuristic for Energy-conscious Single Machine Scheduling Problem under Time-of-use Electricity Tariffs[J].Journal of Cleaner Production, 2016, 129:565-577.
[20] SHROUF F, ORDIERES-MERÉ J, GARC A-S
A-S NCHEZ A, et al.Optimizing the Production Scheduling of a Single Machine to Minimize Total Energy Consumption Costs[J].Journal of Cleaner Production, 2014, 67:197-207.
NCHEZ A, et al.Optimizing the Production Scheduling of a Single Machine to Minimize Total Energy Consumption Costs[J].Journal of Cleaner Production, 2014, 67:197-207.
[21] 刘彩洁, 徐志涛, 张钦,等.分时电价下基于NAGA-Ⅱ的柔性作业车间绿色调度[J].中国机械工程, 2020, 31(5):576-585.
LIU Caijie, XU Zhitao, ZHANG Qin, et al.Green Scheduling of Flexible Job Shop Based on NAGA-Ⅱ under TOU Power Price[J].China Mechanical Engineering, 2020, 31(5):576-585.
[22] CASTRO P M, SUN L, HARJUNKOSKI I.Resource-task Network Formulations for Industrial Demand Side Management of a Steel Plant[J].Industrial & Engineering Chemistry Research, 2013, 52(36):13046-13058.
[23] SHARMA A, ZHAO F, SUTHERLAND J W.Econological Scheduling of a Manufacturing Enterprise Operating under a Time-of-use Electricity Tariff[J].Journal of Cleaner Production, 2015, 108:256-270.
[24] GENG K , YE C , CAO L , et al.Multi-objective Reentrant Hybrid Flowshop Scheduling with Machines Turning On and Off Control Strategy Using Improved Multi-verse Optimizer Algorithm[J].Mathematical Problems in Engineering, 2019:2573873.
[25] CHOI H S, KIM J S, LEE D H.Real-time Scheduling for Reentrant Hybrid Flow Shops:a Decision Tree Based Mechanism and Its Application to a TFT-LCD Line[J].Expert Systems with Applications, 2011, 38(4):3514-3521.
[26] YING K C, LIN S W, WAN S Y.Bi-objective Reentrant Hybrid Flowshop Scheduling:an Iterated Pareto Greedy Algorithm[J].International Journal of Production Research, 2014, 52(19):5735-5747.
[27] PAN J C H, CHEN J S.Mixed Binary Integer Programming Formulations for the Reentrant Job Shop Scheduling Problem[J].Computers & Operations Research, 2005, 32(5):1197-1212.
[28] 节约1度电或1公斤煤等于减排多少二氧化碳[EB/OL].中国碳排放交易网,2013[2019-11-10].http://www.tanpaifang.com/tanjiliang/2013/1215/26997.html.
How Much Carbon Dioxide to Save One kW·h of Electricity or One Kilogram of Coal Is Equivalent to Reducing Carbon Dioxide Emissions[EB/OL].China Carbon Emissions Trading Network,2013[2019-11-10].http://www.tanpaifang.com/tanjing/2013/1215/26997.html.
[29] 袁维海.关于我国电力走节能型发展之路的思考[J].华东经济管理, 2008(12):77-79.
YUAN Weihai.On the Development of Energy-saving Power Walk the Road of Thinking[J].East China Economic Management, 2008(12):77-79.
[30] CHO H M, BAE S J, KIM J, et al.Bi-objective Scheduling for Reentrant Hybrid Flow Shop Using Pareto Genetic Algorithm[J].Computers & Industrial Engineering, 2011, 61(3):529-541.
