0 引言
数控机床是制造业的“工作母机”，在制造过程中数控机床产生大量能耗并造成许多污染和二氧化碳排放，该问题越来越被广大学者重视[1]。在数控机床加工过程中，选择合理的加工参数对于确保产品质量、延长刀具寿命、降低生产成本、减少碳排放和提高生产效率具有重要意义[2]。然而，在实际加工过程中，降低生产成本、减少碳排放和提高生产效率这3个目标之间通常是相互矛盾的，因此，必须通过合理的优化决策方法提供多种切削参数优化组合，以供决策者依据自身情况进行选择以达到需求平衡。
切削参数优化问题从20世纪末开始得到国内外学者的广泛关注。ASOKAN等[3]在切削力、切削刃温度和主轴功率的约束下，结合模拟退火算法和遗传算法，以最小生产成本为目标进行了切削用量的优化研究。刘海江等[4]建立了以进给量和切削速度为变量、以最大生产率和最低生产成本为优化目标的多目标优化模型，应用粒子群算法对数学模型进行寻优求解，证明了粒子群算法适用于解决复杂的非线性优化问题。YILDIZ等[5]提出了一种基于教学优化(teaching-learning-based optimization，TLBO)算法与田口方法的混合优化算法，用于求解切削加工多目标优化问题。
进入21世纪后，环境污染和资源枯竭问题开始得到重视[6]，对于切削参数优化问题的研究在优化加工时间、成本等经济型指标的同时也开始考虑能耗等环境指标。RAJEMI等[7]建立了机械加工过程总能耗模型，提出了一种通过提高刀具使用寿命来获得最小能源足迹的切削参数优化方法。李聪波等[8]采用复合形法，以车削加工中低碳、高效为优化目标，对切削参数进行了灵敏度分析。YAN等[9]采用曲面响应法和加权灰色关联法，建立了能耗、加工质量和生产效率铣削多目标优化模型。HANAFI等[10]利用灰色关联理论和田口方法研究了可持续加工的切削条件优化，旨在实现最小加工能耗和最佳表面质量。LIU等[11]提出了一种多目标优化模型，以同时优化最小切削能耗、表面粗糙度以及最大材料去除率。
综上所述，当前大部分对于切削加工过程的切削参数优化问题的研究仍主要以生产成本、工艺时间和加工质量等经济性指标为目标，以碳排放等环境性指标为目标同时兼顾经济性指标的研究尚未引起广泛关注。在目前资源紧缺的严峻形势下，深入研究环境性指标和经济性指标具有重大意义。
本文在刀具寿命、铣床工艺能力和加工质量等条件约束下，以单位体积碳排放、单位体积生产成本和加工时间为优化目标，建立了铣削加工参数多目标优化模型，提出了一种改进的非支配排序引力搜索算法(improved non-dominated sorting gravity search algorithm, INSGSA)求解该模型，并将本文算法与原始非支配排序引力搜索算法(non-dominated sorting gravity search algorithm, NSGSA)、TLBO进行了对比。
1 构建铣削加工参数多目标优化模型
1.1 选择优化变量
在数控铣削加工过程中，切削速率vc、每齿进给量fz和切削宽度ae是影响铣削加工中生产效率、生产成本和碳排放的主要控制因素[12]。合理的切削参数组合能够实现铣削加工过程中各个目标的协调，在提高生产效率的同时降低生产成本和环境污染。因此，笔者将切削速率vc、每齿进给量fz和切削宽度ae这3个参数作为本研究的优化变量。
1.2 优化目标
1.2.1 工艺时间目标函数
在批量生产中，生产效率可用完成一道工序所需的平均铣削加工时间Tave表示[12]：
Tave=Tp+Tl+Ta+Tm+Tc
(1)
式中，Tp为单个工件完成一道工序所需要的平均加工准备时间；Tl为单个工件完成一道工序所需要的工件装夹和拆卸平均时间；Ta为单个工件完成一道工序所需要的工艺调整和快进快退平均时间；Tm为单个工件完成一道工序所需要的切削作业平均时间；Tc为单个工件完成一道工序所需要的因刀具报废导致的实际换刀时间。
(1)加工准备时间
(2)
式中，Ts为批量生产的准备总时间；Nb为生产批量。
(2)切削作业时间
(3)
式中，L为铣削加工的工步步长；vf为铣床进给速率；B为铣削面积的宽度。
(3)实际换刀时间
(4)
(5)
式中，Td为完成一次换刀动作所需的时间；T为刀具寿命；Cv为刀具寿命矫正系数；λs为刃倾角；Dt为刀具直径；z为刀具齿数；m、bv、Bm、Bp、Bh、Bt、ap、ev、uv、qv、nv为常数。
联立以上各式可得
(6)
平均铣削加工时间Tave越短，生产效率越高。
1.2.2 单位体积碳排放目标函数
机床铣削加工过程碳排放是指在铣削过程中因生产和消耗物料等产生的直接和间接碳排放，主要包括了由电能消耗引起的碳排放、刀具磨损引起的碳排放、坯料制备引起的碳排放、切削液使用引起的碳排放和废屑处理引起的碳排放5个部分[13]。
本文主要研究切削参数对碳排放的影响，而坯料制备与废屑处理阶段产生的碳排放量的优化空间有限，因此在本文的碳排放计算模型中不考虑这两部分的碳排放量。
铣削过程的单位体积碳排放
SCE=CE/V
(7)
CE=Cf+Ct+Cel
(8)
式中，CE为铣削加工过程的碳排放量；V为铣削加工体积，铣削加工形状为长方体，V=HBL；H为铣削高度；B为铣削宽度；L为铣削长度；Cf为切削液使用引起的碳排放；Ct为刀具磨损引起的碳排放；Cel为电能消耗引起的碳排放。
(1)切削液使用引起的碳排放[13]
(9)
Cw=Fw[(Ac+Cc)/δ]
(10)
Co=Fo(Ac+Cc)
(11)
式中，Tf为切削液更换周期；Cw、Co分别代表废弃切削液处理产生的碳排放量和切削液中的矿物油制备所产生的碳排放量；Fw为废弃切削液处理过程中的碳排放因子(单位质量物质伴随的温室气体的生成量)；Ac为最新添加矿物油的容量；Cc为原始矿物油的容量；δ为切削液矿物油的浓度；Fo为切削液中矿物油制备过程中的碳排放因子。
(2)刀具磨损引起的碳排放
(12)
式中，Mt为刀片质量；Ft为刀具生产过程中的碳排放因子。
(3)电能消耗引起的碳排放
(13)
Ec=El+Em+Ea
(14)
(15)
(16)
(17)
式中，Fe为发电和配电传输过程中的碳排放因子；Ec为铣削加工中的能耗；El为工件装夹、拆卸与换刀能耗；Em为切削作业能耗；Ea为工艺调整和快进快退能耗；Pl、P2、P3分别为工件装夹、拆卸与换刀阶段，切削作业阶段、工艺调整和快进快退阶段的平均功率。
各阶段平均功率的通用模型：
(18)
式中，Pa为待机功率；kl、k2分别为主轴系统的一、二阶功率损耗系数；k3、k4分别为进给系统的一、二阶功率损耗系数；Bj为第j个辅助系统的功率；na为辅助系统的数量；Cj为相应系统的模态；fP(f,Zf)为变频器功率损耗量，通常变频器的能量效率为92%；m为电机相数；Im为励磁电流；Rm为励磁电阻；α为机床载荷损耗系数；n为主轴转速；ap为切削深度；x、y、w、u分别为vc、fz、ap、ae的影响系数。
1.2.3 单位体积生产成本目标函数
在面向绿色制造的铣削加工参数优化中，只注重其环境指标而忽略其经济性是极其不科学的。单位体积生产成本(SPC)是衡量企业技术和管理水平的重要指标。在铣削加工过程中，单位体积生产成本SPC主要包括坯料成本、电能成本、刀具成本、切削液成本、人工成本和机床折旧成本：
SPC=(Cmat+Cpower+Ctlc+Cfd+Cla+Cmt)/V
(19)
式中，Cmat为坯料成本；Cpower为电能消耗成本；Ctlc为刀具损耗成本；Cfd为切削液成本；Cla为人工成本；Cmt为机床折旧成本。
(1)电能成本
(20)
式中，Cp为电能单价；Ec为单位能耗。
(2)刀具损耗成本
(21)
式中，Ctc为刀具成本。
(3)切削液成本
(22)
式中，Cfc为单位体积切削液成本。
(4)人工成本
Cla=Tave(Ca+Cl)
(23)
式中，Ca为单位时间的管理成本；Cl为单位时间的劳动成本。
(5)机床折旧成本
Cmt=CbTave
(24)
式中，Cb为铣床单位时间的折旧成本。
1.3 约束条件的确定
在铣削加工过程中，铣刀会受到刀柄强度和刀柄许用挠曲的约束，铣床主轴的功率不应超过最高功率。因此，为了在铣削加工过程提高生产效率降低碳排放的同时，使优化结果尽可能贴近实际生产，对铣削加工的约束条件设置如下：
(1)主轴功率约束
Pc≤ηPm
(25)
式中，η为机床主传动链效率；Pm为机床额定功率。
(2)主轴转速约束
nmin≤n≤nmax
(26)
式中，nmin为铣床主轴最低许用转速；nmax为铣床主轴最高许用转速。
铣床的切削速率主要由主轴转速决定，因此切削速率vc的取值范围为
(3)切削宽度约束。为了避免在铣削过程中刀具承受载荷过大，切削宽度ae不应过大：
ae≤0.8Dt
(27)
(4)刀柄挠曲约束
(28)
式中，Fd为刀柄挠曲许用应力；E为刀柄材料弹性模量；e为刀柄许用挠度；La为刀柄两支点距离；da为刀柄直径。
(5)刀柄强度约束
Fc≤Fs
(29)
式中，Fs为铣刀刀柄屈服强度对应的许用应力；Fc为铣削过程中的平均切削力。
基于上述研究讨论，数控铣床平面加工工艺参数多目标优化模型如下：
(30)
2 多目标非支配排序引力搜索算法
2.1 原始算法的基本思想
RASHEDI等[14]在2009年受到万有引力定律的启发，提出了一种新的群体进化算法----万有引力搜索算法(简称“引力搜索算法”)。该算法在求解优化问题的时候，搜索质点的位置对应优化问题的解，质点的质量用来衡量质点的优劣，位置越好，质点所对应的质量越大。整个群体依靠质点之间的引力作用进行寻优操作，在质点之间的相互吸引作用下，整个群体会朝着质量最大的质点方向移动，通过其内在的搜索机制，最终整个群体都会围绕在质量最大的质点周围，从而得到位置最好的质点，达到寻优的目的。作为一种通用型优化算法，引力搜索算法从提出到现在已经在一系列复杂的优化问题的求解中取得了良好的效果[15]。
2.2 原始算法的模型
在解空间和速度空间对速度进行初始化是算法的第一步，在一个D维空间中，第i个搜索质点的位置和速度分别表示为[13]
(31)
(32)
式中，
为质点i在第d维度的位置分量；
为质点i在第d维度的速度分量。
通过评价每个质点的目标函数值，确定质点的质量和受到的引力，计算加速度，更新质点的速度和位置。
2.2.1 质点质量计算
在原始引力搜索算法中，第i个质点的惯性质量Mi由其自身和整个质点群的适应度值确定，其定义如下：
(33)
(34)
式中，fiti(t)为第t次迭代时第i个质点的适应度函数；qi(t)为第t次迭代时第i个质点的相对适应度函数；Mi(t)为第t次迭代时第i个质点的惯性质量；N为质点群的质点数量；best(t)和worst(t)分别为第t次迭代中所有质子中最优适应度函数和最差适应度函数。
对于求解最小化目标函数优化问题，定义如下：
best(t)=minfitj(t)
(35)
worst(t)=maxfitj(t)
(36)
2.2.2 质点引力计算
引力搜索算法受到万有引力定律的启发，但不被其在物理学中的精确公式束缚，RASHEDI等[14]通过标准测试集证实在引力搜索算法中采用两个质点间的距离r比r2算法收敛效果更好。因此，在任意迭代时刻t，质子j对质子i在第d维上的引力
定义如下：
(37)
式中，Mi(t)、Mj(t)分别为质点i和质点j的质量；G(t)为第t次迭代时的万有引力常数，G(t)=G0e-at/Nt，G0和a为常数，Nt为最大迭代次数，为了控制算法的搜索精度，G(t)和随着迭代次数的增加不断减小；Rij(t)为两个质点之间的欧氏距离，i，j∈{1,2,…,N}，且i≠j；ε为一个极微小的常数。
在引力搜索算法中，质点i在第d维受到的吸引力表示为
(38)
(39)
式中，randj表示在[0，1]区间服从均匀分布的随机变量；kbest(t)为第t次迭代时质点质量按降序排列的前k个质点；tmax为迭代终止次数。
kbest(t)的取值随着迭代次数的增加线性减少。在搜索前期充分勘探整个搜索空间，随着搜索的进行，逐渐从全局勘探转向局部开发以获得最优解。
2.2.3 质点加速度计算
根据牛顿第二定律，质点i在第d维度上的加速度方程为
(40)
2.2.4 质点速度和位置更新
为了提高寻优的有效性，有必要加强质点速率的随机性，在质点的速度迭代过程中引入一个在[0，1]之间服从均匀分布的随机变量rd：
(41)
式中，
为第t次迭代时第i个质点在第d维的速度；
为第t次迭代时第i个质点在第d维的加速度。
质点i在第d维的更新方程：
(42)
式中，
为第t次迭代时第i个质点在第d维的位置。
2.3 改进的非支配排序引力搜索算法
NOBAHARI等[16]于2011年提出了一种非支配排序引力搜索算法(NSGSA)用于解决多目标优化问题，该算法主要是引入了非支配排序、Pareto解集和拥挤距离等思想，并改进了质点惯性质量的评价方法。
2.3.1 非支配排序方法与拥挤距离
对于多目标优化问题，目标之间可能存在冲突，无法找到一个解使得所有的目标函数同时达到最优，因此，对于多目标优化问题，通常存在一个解集，这些解之间就全体目标函数而言是无法比较优劣的，这种解称作非支配解(non-dominated solution)或者Pareto 最优解(Pareto optimal solution)。
处理多目标优化问题时，需要分析群体中质点之间的非劣关系，NSGSA算法将质点分为多个层级，分配方法如下：对当前群体中所有质子中没有被其他任何质子所支配的质子，定义其非支配等级R=1，非支配等级R=1的质点集合即为第一层Pareto-占优集合；将这些质点从群体中移除，对群体余下的质点按照上述方法进行处理，得到第二层Pareto-占优集合；以此类推，直到群体中所有的质点都有了非支配等级。
群体在空间的分布情况对于Pareto-最优前沿的分布影响巨大，为了描述群体中质点在空间的分布情况，NSGSA算法引入了拥挤距离来刻画个体之间的密集程度。一般来说，质点的拥挤距离越大其密集程度小。在非支配排序分层的基础上，质点的拥挤距离可以通过处于同一层级的与其相邻的两个个体在每个子目标上的距离之和来计算。设I(i)dt为第i个质点的拥挤距离，I[i]k为第i个质点在第k个子目标的函数值。当多目标优化问题具有s个子目标时，第i个质点的拥挤距离I(i)dt可表示为
(43)
式中，
和
分别表示第k个子目标函数值的最大和最小值；I(i+1)k为第i+1个质点在第k个子目标的函数值，I(i-1)k为第i-1个质点在第k个子目标的函数值。
比较两个质点时，取非支配等级高(R值小)的质点，如果质点处于相同的非支配等级则取拥挤距离大(密集度小)的质点。由此可以得到第i个质点和第j个质点的偏序关系当满足以下两个条件之一：
I(i)rank<I(j)rank
(44)
I(i)rank=I(j)rank 且 I(i)dt>I(j)dt
(45)
那么称第i个质点优于第j个质点，其中I(i)rank为第i个质点的非支配等级，I(j)rank为第j个质点的非支配等级。
通过比较非支配排序等级和拥挤距离，设置非支配排序等级高、拥挤距离大的质点拥有更小的适应度值，也即更大的惯性质量。
2.3.2 外部归档集合的更新
NSGSA算法使用一个长度有限的外部归档集(external archive)来存储迭代过程中产生的非支配解。如果外部归档集中的某一个质点或者某几个质点被移动质点支配，那么这些被支配的质点将被移出外部归档集。当非支配解的数量超过外部归档集的长度时，需要从归档集最拥挤的区域移除部分质点，使外部归档集的分布更加均匀。
2.3.3 更新移动质点集合
在移动质点集合迭代更新操作中，为了提高算法的精英特性，需从外部归档集合中选取优质质点插入移动质点集合中。首先，将外部归档集中的c个极值点和c个拥挤距离最大的质点插入到移动质点集合中以扩展Pareto前沿。然后在外部归档集合中随机选取一定精英率Pel的非支配质点作为精英质点插入到移动质点集合中引导Pareto前沿向真实Pareto前端前进。相对应地，通过比较质点的偏序关系，从移动集合中移除同等数量的劣等质点以保证移动质点集合长度不变。
为了提高算法群体的多样性，受遗传算法的启发，本文首次提出了精英-精英交叉策略和精英-非精英交叉策略产生优质质点来增加群体的多样性。
精英-精英交叉策略如图1所示，在外部归档集合中随机选取部分质点作为精英质点，然后对选取出来的精英质点之间的位置进行交叉得到一定精英-精英交叉新质点比例Pe-e的新质点，将这些新的质点加入移动质点集合中。
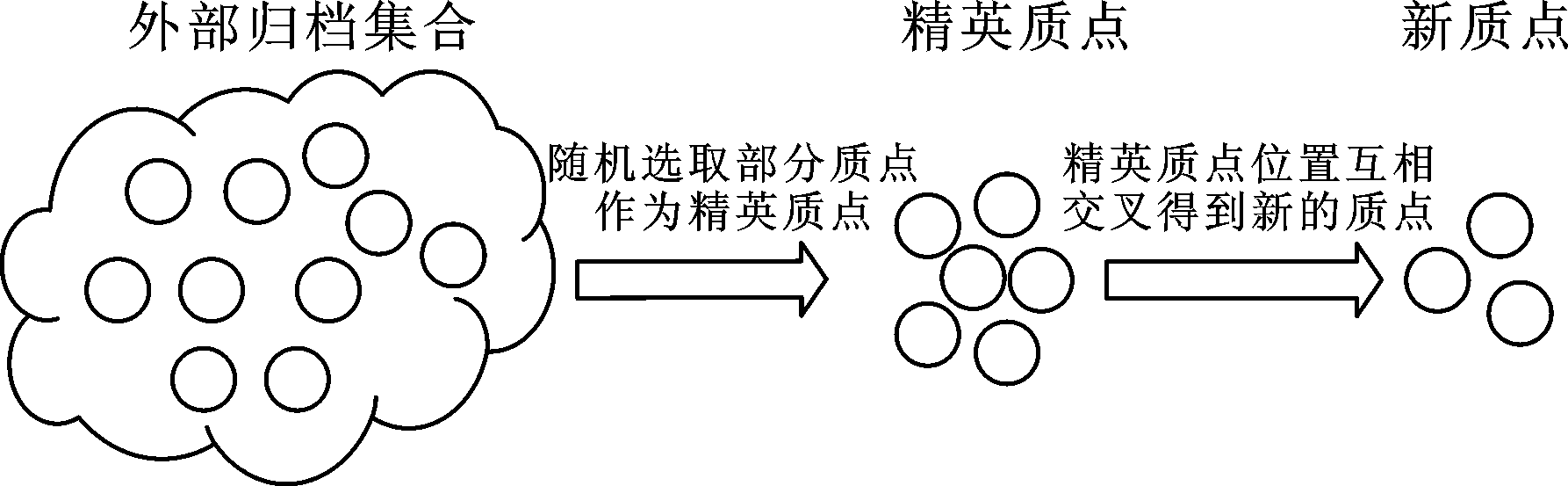
图1 精英-精英交叉策略
Fig.1 Elite-elite cross strategy
精英-非精英交叉策略如图2所示，在外部归档集合中随机选取部分质点作为精英质点，随机选择群体中被支配的部分质点作为非精英质点，对选取出来的非精英质点与精英质点的位置进行交叉得到一定精英-非精英交叉新质点比例Pe-n的新质点，将这些新的质点加入移动质点集合中。
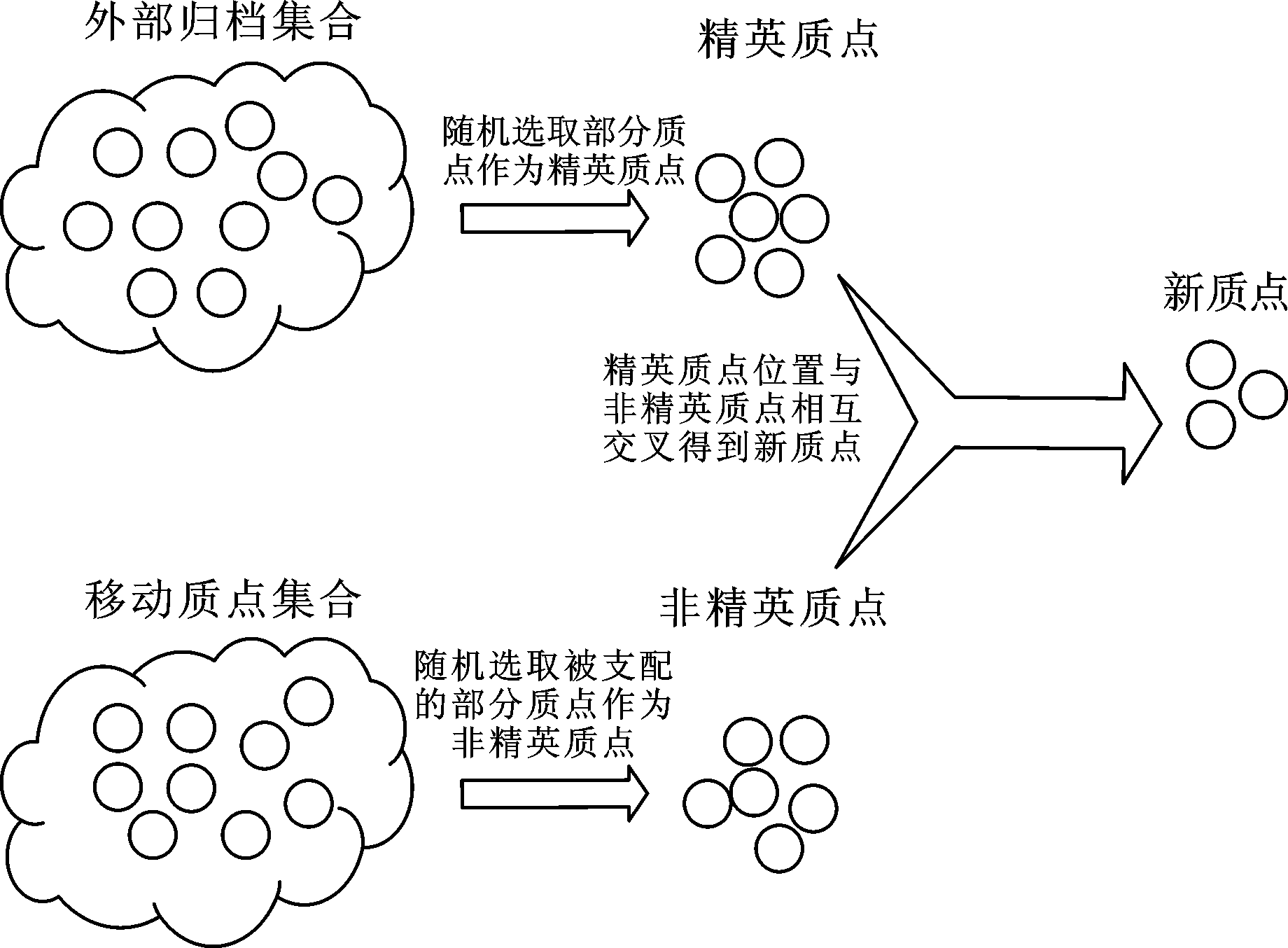
图2 精英-非精英交叉策略
Fig.2 Elite-non-elite cross strategy
另外，优质质点在插入移动质点集合后，需将其各个维度的速度分量初始化为零。
2.3.4 移动质点的惯性质量和加速度
一般情况下，惯性质量函数可通过适应度函数值来定义。设计适应度函数时应充分考虑使Pareto前沿与Pareto真实前沿的距离尽可能小并要求其分布均匀，NSGSA算法通过非支配排序和拥挤距离定义其适应度函数。根据非支配排序和拥挤距离确定移动集合中各个质点的偏序关系，将偏序等级最高的质点的适应度函数值设置为1，偏序等级第二高的质点的适应度函数值设置为2，以此类推，直至群体中所有质点的适应度函数值都设置完毕。最后设置各个质点的惯性质量为其适应度函数值的倒数。NSGSA算法更新加速度的公式与式(41)一致。
2.3.5 移动质点的进化与变异
一般而言，多目标优化算法在进化前期应关注全局的勘探，而随着迭代的进行，应逐步将专注点从全局勘探转向局部的开发来寻找最优解。因此，NSGSA算法为了保证收敛速度和收敛精度，在质点群算法惯性权重改进方法的启发下，将移动质点的速度更新公式设置如下：
(46)
式中，为第t次迭代时第i个质点在第d维的加速度;wmax、wmin分别为最大和最小权重。
在NSGSA算法中移动质点的位置更新公式如下：
(47)
NSGSA算法与其他经典启发式算法一样存在早熟的缺陷，为了解决这个问题，降低算法陷入局部最优的几率，本文在NSGSA算法的基础上引入了一个新的位置坐标变异邻域结构进行局部搜索，充分发挥算法全局搜索的特性和邻域搜索局部精细搜索的特性：
(48)
式中，搜索半径rs>0；θ在[0，2π]之间随机生成；Rp1为在[0，1]区间服从均匀分布的随机变量；Pp为位置更新变异率。
更新位置坐标后的移动质点不一定优于更新前的移动质点，极有可能出现退化现象，即新产生的质点劣于原先的质点。为了减少算法的退化现象，引导着群体质点向真实的Pareto前沿靠近，本文在模拟退火算法思想的启发下提出了位置更新回退策略：
(49)
(50)
式中，Pg为位置更新率；iafter>ibefore表示更新后的质点支配更新前的质点；Pk为常数，取值范围为[0,1]；xi(t+1)为第t+1次迭代中质点i的位置；xi(t)为第t次迭代中质点i的位置；Rp2为在[0,1]之间服从均匀分布的一个随机变量。
2.3.6 改进算法的实现流程
(1)初始化改进算法的参数，包括搜索空间的维数、外部归档集长度和迭代次数等。
(2)随机初始化群体的各个质点的位置，并将质点的初始速度和加速度设置为零。
(3)对群体中所有的质点进行非支配排序，并计算拥挤距离，进行质点适应度赋值。
(4)计算质点惯性质量、受到的引力和加速度。
(5)采用改进的策略对质点的速度和位置进行更新。
(6)若当前迭代次数没有达到设定的最大迭代次数，则重复步骤(3)～步骤(5)；否则退出循环迭代，输出当前外部归档集。
图3为改进的非支配排序引力搜索算法流程。
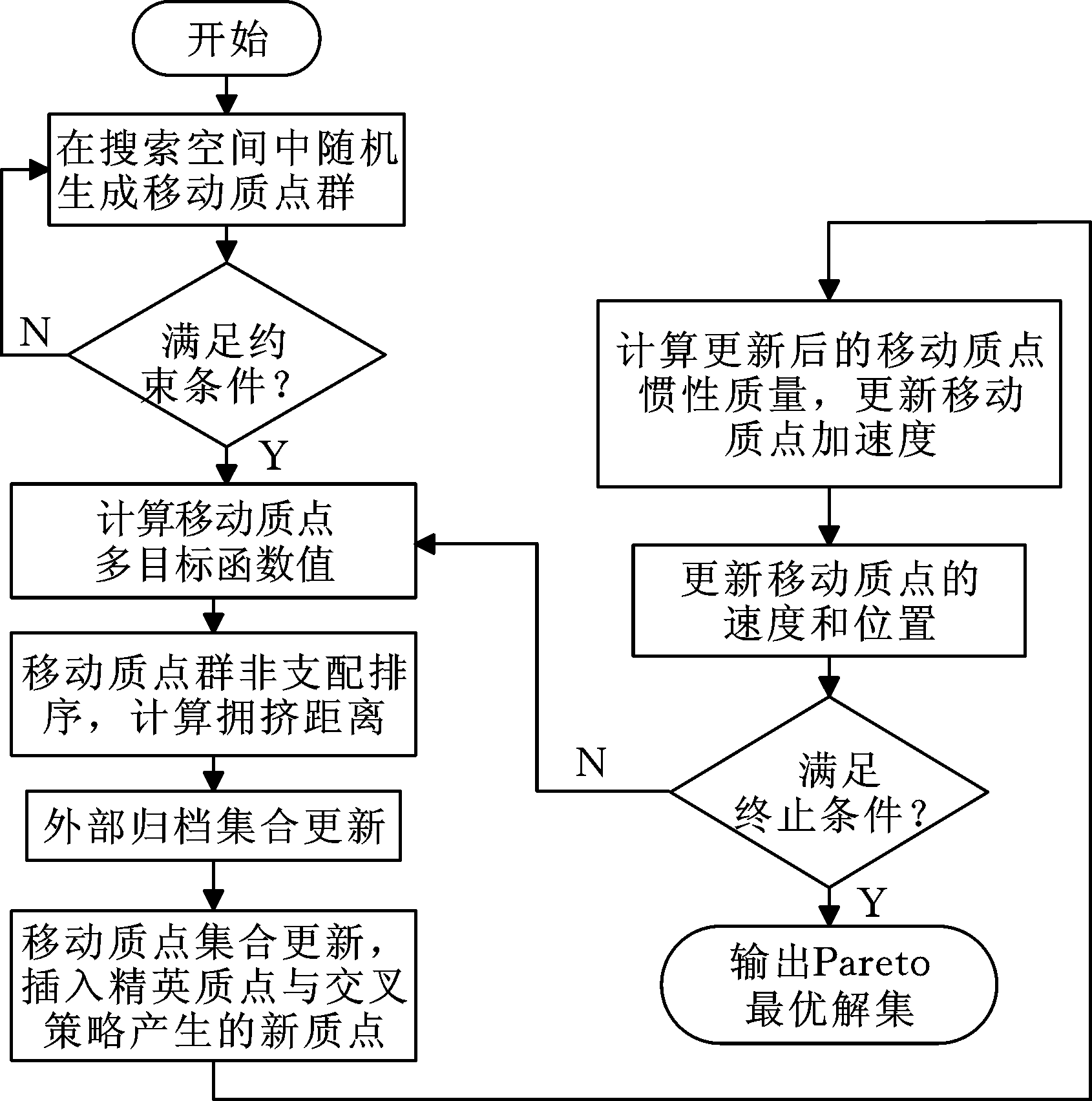
图3 INSGSA算法流程图
fig.3 INSGSA algorithm flowchart
3 铣削加工多目标参数优化实例验证
3.1 铣削参数设置
铣削加工的工艺参数和模型参数来自文献[17]。数控铣床系统加工相关参数见表1。功率损耗η的相关系数kl=1.01×10-1，k2=2.08×10-6，k3=1.09×10-2，k4=2.32×10-7。刀具材料为HSS，刀具直径Dt=63 mm，刀片质量mt=0.009 2 kg，其余刀具参数见表2。表3为工件相关系数。表4为铣削加工相关参数。表5为碳排放相关参数。表6为成本计算相关参数。
表1 数控铣床系统加工相关参数
Tab.1 Parameters of CNC milling machine system
机床主传动链效率η机床额定功率Pm(kW)机床固定功率P0(W)机床载荷损耗系数α主轴转速范围n(r/min)进给速率范围vf(mm/min)0.75.54481.231.5～200014～900
表2 刀具相关参数
Tab.2 Parameters of the tool
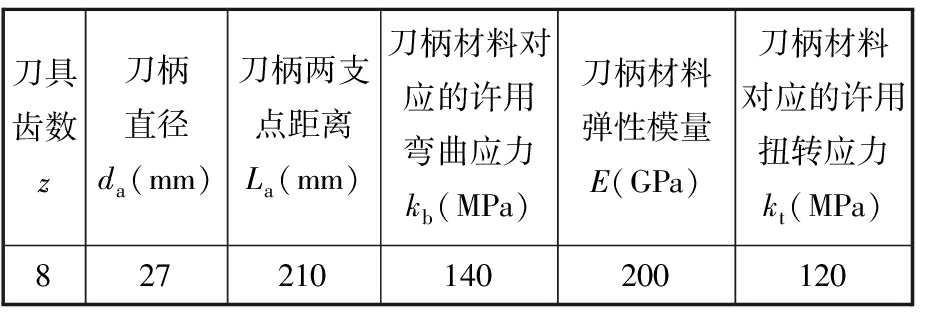
刀具齿数z刀柄直径da(mm)刀柄两支点距离La(mm)刀柄材料对应的许用弯曲应力kb(MPa)刀柄材料弹性模量E(GPa)刀柄材料对应的许用扭转应力kt(MPa)827210140200120
表3 工件相关参数
Tab.3 Parameters of the workpiece
材料布氏硬度(MPa)抗拉强度(MPa)铣削加工工步长度L(mm)切削深度ap(mm)C#0.6%1502101600.5
表4 铣削加工相关参数
Tab.4 Processing parameters of the milling
工件装夹和拆卸时间Tl(min)批量生产的准备总时间Ts(min)工艺调整和快进快退时间Ta(min/part)一次完整换刀动作时间Td(min)生产批量Nb1.5100.15100
表5 碳排放相关参数
Tab.5 Processing parameters of carbon emission
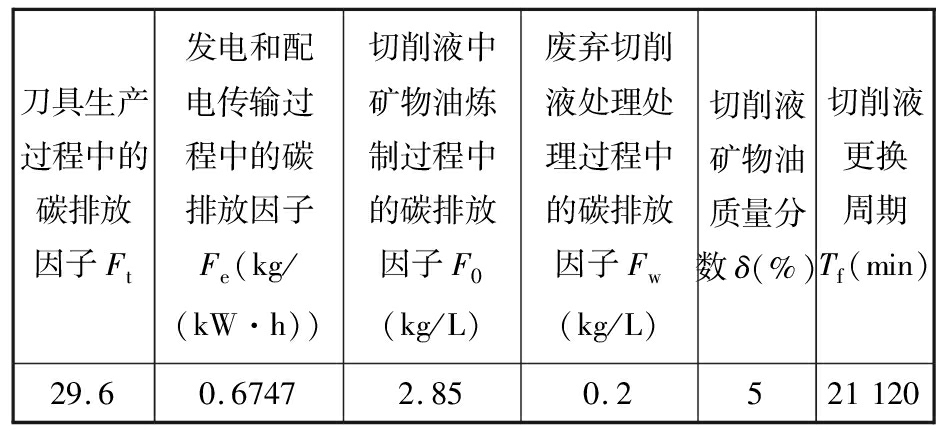
刀具生产过程中的碳排放因子Ft发电和配电传输过程中的碳排放因子Fe(kg/(kW·h))切削液中矿物油炼制过程中的碳排放因子F0(kg/L)废弃切削液处理处理过程中的碳排放因子Fw(kg/L)切削液矿物油质量分数δ(%)切削液更换周期Tf(min)29.60.67472.850.2521120
表6 成本计算相关参数
Tab.6 Parameters of cost calculation
坯料成本Cmat电能单价Cl(min-1)刀具成本Ctc单位体积切削液成本Cfc(L-1)单位时间的劳动成本Cl(min-1)单位时间的管理成本C0(min-1)单位时间机床折旧成本Cb(min-1)100.075009.50.451.450.25
其他参数设置：Cc=8.5 L，Ac=4.5 L，Bm=1，Bk=1，Bp=0.8，ev=0.3，rv=0.1，uv=0.4，nv=0.1，Cv=35.4，qv=0，bv=0.45，Czp=68.2，m=0.33，bz=-0.86，nz=1，rz=1，ez=0.86，uz=0.72，bz=-0.86，λs=30°。
3.2 改进算法参数设置
INSGSA改进优化算法在Ubuntu 16.04操作系统，Core i5 CPU，8G内存笔记本电脑上运行，采用Java语言实现。INSGSA算法的相应参数设置见表7。
为了证明本文提出的INSGSA算法求解多目标优化问题的优越性，将该算法与NSGSA和TLBO算法对比。NSGSA的参数设置为：符号变异率Ps=0.2，次序变异率Po=0.1，位置变异率Pu=0.01，精英率Pel=0.5，其余参数与INSGSA一致。TLBO参数设置采用文献[18]中推荐的参数设置：群体规模为100，最优解集长度为100，最大迭代次数与其余两个算法一致均为250。
表7 INSGSA算法参数
Tab.7 INSGSA parameters
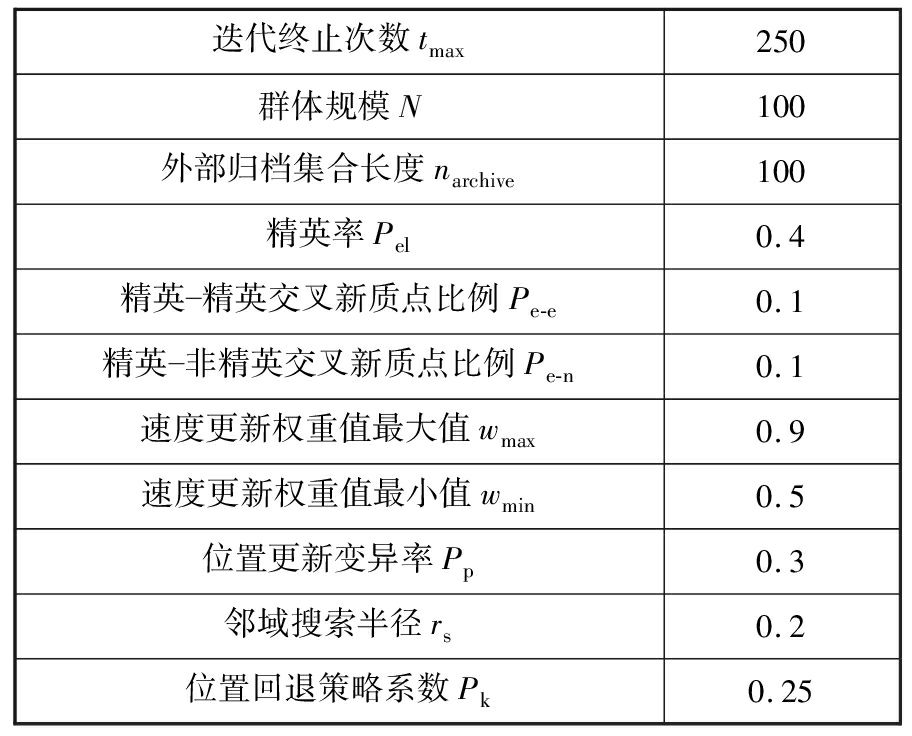
迭代终止次数tmax250群体规模N100外部归档集合长度narchive100精英率Pel0.4精英精英交叉新质点比例Pe-e0.1精英非精英交叉新质点比例Pe-n0.1速度更新权重值最大值wmax0.9速度更新权重值最小值wmin0.5位置更新变异率Pp0.3邻域搜索半径rs0.2位置回退策略系数Pk0.25
3.3 优化结果分析
若需要优化的目标函数之间不存在任何冲突关系，则失去了多目标优化问题研究的意义，因此，必须先确定每个优化目标函数与其余2个优化目标函数之间的关系。直接进行3个铣削参数优化目标函数之间的分析，将难以确认优化目标函数间的冲突关系，因此，首先分析优化目标函数两两之间的关系，然后再进行3个优化目标函数间的分析。
使用INSGSA、NSGSA和TLBO算法优化生产时间和单位体积碳排放双目标函数，图4为3种算法的Pareto-最优前端。由图4可知生产时间目标和单位体积碳排放目标基本是负相关的，生产时间越短，单位体积碳排放量越大，反之亦然。INSGSA算法所得到的Pareto-最优前端分布均匀且范围更广。NSGSA算法得到的Pareto-最优前端部分解劣于INSGSA算法，其前端分布不均。TLBO算法得到的Pareto解集明显劣于其他两个算法得到的解集。
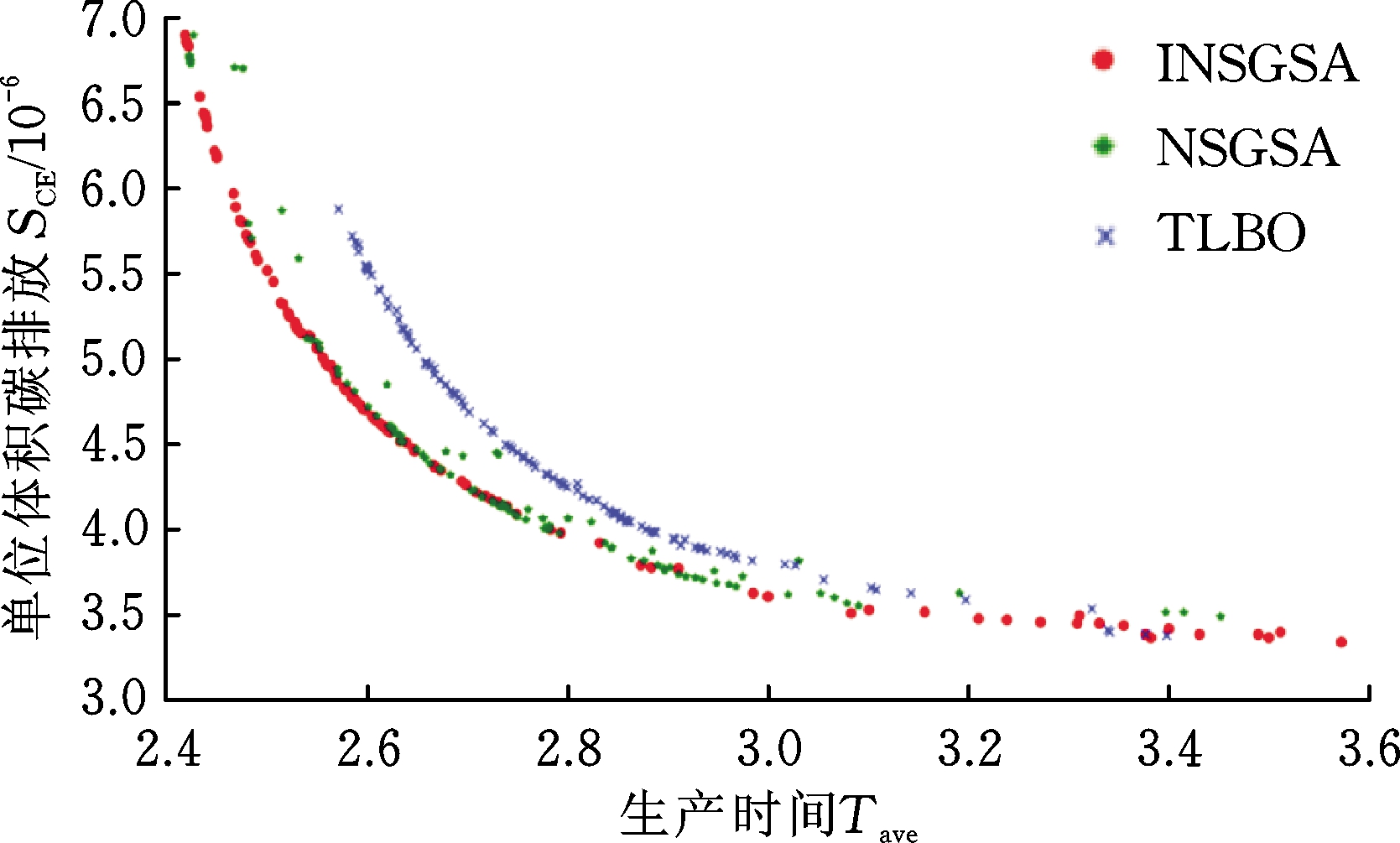
图4 生产时间和单位体积碳排放双目标函数优化结果
Fig.4 Optimization results of dual objective function for production time and carbon emissions per unit volume
同样使用INSGSA、NSGSA和TLBO算法优化生产时间和单位体积生产成本双目标函数，图5为3种算法的Pareto-最优前端。由图5可知，生产时间目标和单位体积生产成本目标基本是负相关的，生产时间越短，单位体积生产成本越高。INSGSA算法所得到的Pareto-最优前端分布均匀且范围更广，其Pareto解集明显优于NSGSA算法和TLBO算法。NSGSA算法得到的Pareto-最优前端分布不均。TLBO算法得到的Pareto-最优前端过于集中且明显劣于其他两个算法的Pareto-最优前端。
图5 生产时间和单位体积生产成本双目标函数优化结果
Fig.5 Optimization results of dual objective function of production time and production costs per unit volume
图6 单位体积碳排放和单位体积生产成本双目标函数优化结果
Fig.6 Optimal results of dual objective function for carbon emissions per unit volume and production costs per unit volume
同样使用3种算法优化单位体积碳排放和单位体积生产成本双目标函数，图6为3种算法得到的Pareto-最优前端。3种算法得到的Pareto解集都只存在一个解。分析单位体积碳排放模型和单位体积生产成本模型，电能消耗引起的碳排放Ce和单位能耗Ec成正比，电能成本Cpower与单位能耗Ec成正比，单位体积碳排放模型中的切削液使用引起的碳排放Cf和刀具磨损引起的碳排放Ct分别与单位体积生产成本模型中的切削液成本Cfd、刀具损耗成本Ctlc呈正相关，因此可知单位体积碳排放目标和单位体积生产成本目标基本不存在冲突。在图6中，INSGSA算法得到的解集可以支配其他两个算法得到的解，同样也证明了INSGSA算法的优越性。
综合以上的分析可以得知3个目标函数之间的冲突关系为：生产时间目标与单位体积碳排放和单位体积生产成本这两个目标基本是呈负相关的，而单位体积碳排放目标与单位体积生产成本目标不存在冲突。
分别使用3种算法优化单位体积碳排放、单位体积生产成本和加工时间多目标函数。图7为INSGSA、NSGSA和TLBO算法的Pareto-最优前端。由图7可知INSGSA和NSGSA算法得到的Pareto解集均匀分布在Pareto-前端，而TLBO算法得到的Pareto解在Pareto前端分布不均且远离Pareto-最优前端，说明了INSGSA和NSGSA算法均能有效解决铣削加工多目标优化问题，TLBO算法用来解决铣削加工多目标优化问题效果较差。对比INSGSA和NSGSA算法的Pareto解集分布情况，可知INSGSA算法获得的Pareto前端分布范围更大，说明了本文提出的改进算法获得的群体多样性更优。然而从图中依旧难以明显看出INSGSA算法和NSGSA算法的优劣。
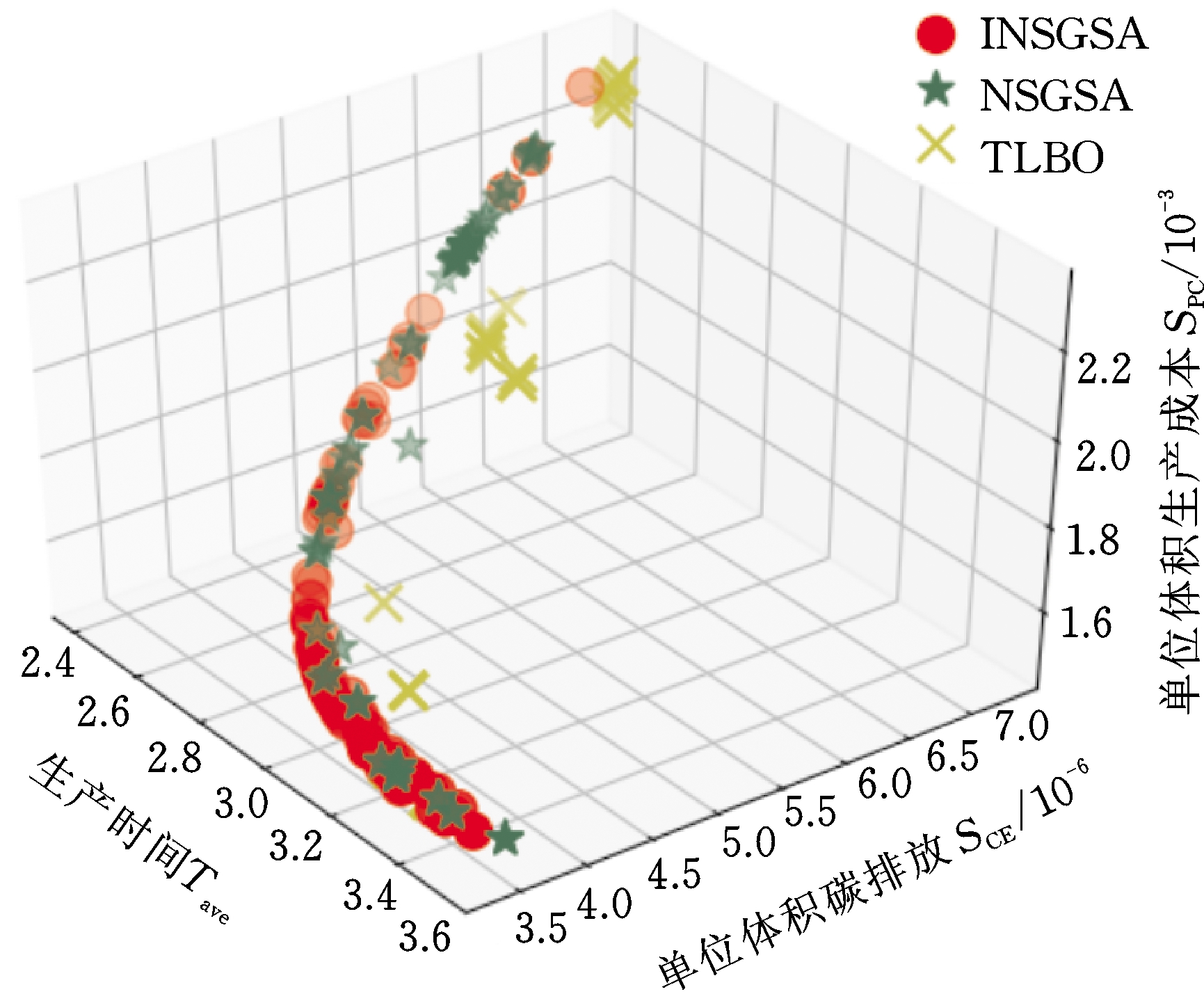
图7 3种算法的Pareto-最优前端图
Fig.7 Pareto-optimal front-end graph of three algorithms
因此本文采用在多目标算法中常用的评价指标:平均Pareto距离Vpd、非支配解数量Vnp和非支配解比例Vrd来比较3种算法的性能。令A(j)为参与比较的算法求得的非支配解集，参考集Ap是将所有参与比较的算法所求得的非支配解集合并，并对其进行非支配排序所得的非支配解集。
(1)平均Pareto距离Vpd。用来衡量算法获得的非支配解集的分布程度，该指标值越小，说明算法得到的解集分布性越好且更接近于参考解集Ap。第j个算法的平均Pareto距离
的求解公式如下：
(51)
(52)
y∈Ap
式中,
和
分别对应参考集Ap中第i个目标函数的最大值与最小值；fi(x)对应解的第i个目标函数值。
(2)非支配解数量Vnp。指算法的非支配解集中不被参考集Ap中任意解支配的解的数量。第j个算法的非支配解数量
的求解公式如下：
(53)
(3)非支配解比例Vrd。指的是算法的非支配解集中非支配解数量Vnp占参考集Ap的比例，非支配解比例越大，算法性能越好。第j个算法的非支配解数量
的求解公式如下:
(54)
为了尽量减少算法随机性对评价指标结果的影响，取算法多次运行的平均结果作为评价指标，即为非支配解平均数量
非支配解平均比例
和Pareto平均距离
设定算法运行次数t=100。
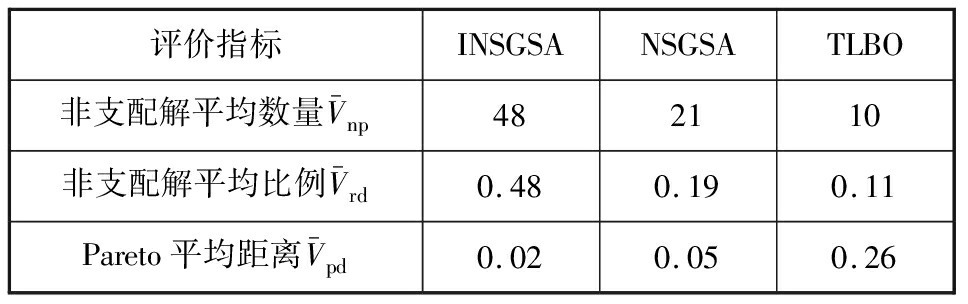
由表8中3种算法的评价指标结果可以看出，针对最小单位体积碳排放、最小单位体积生产成本和最小生产时间多目标铣削参数优化问题，INSGSA算法的Pareto平均距离
指标略小于NSGSA算法，明显小于TLBO算法所得的结果。评价指标结果证明本文提出的精英-精英交叉策略和精英-非精英交叉策略提高了算法群体的多样性，改进后的算法得到的Pareto解集分布均匀性明显好于其他两个算法。同时改进算法得到的Pareto解集相对于其他两个算法更加接近于Pareto-真实前端，说明本文引入的新的位置坐标变异邻域结构和位置更新回退策略在一定程度上减少了算法陷入局部最优和退化的情况。INSGSA算法得到的非支配解集中非支配解平均数量
和非支配解平均比例也明显大于其他两个对比算法得到的结果，证明了本文提出的改进算法具有优越的性能。
表8 3种算法的评价指标结果
Tab.8 Evaluation index results of three algorithms
评价指标INSGSANSGSATLBO非支配解平均数量V-np482110非支配解平均比例V-rd0.480.190.11Pareto平均距离V-pd0.020.050.26
综上所述，本文所提出的改进算法INSGSA在解决铣削加工多目标参数优化问题上，具有较高的算法性能，收敛性与Pareto解集分布均匀性均优于原始NSGSA算法和TLBO算法。
3.4 多目标决策分析
灰色关联分析法属于灰色系统理论的一个分支，该方法通过评价比较数列与其他参考数列的相似程度来确定数列之间是否紧密。
在多目标优化问题中，由nh个可行方案，每个方案中由mh个决策变量，形成决策矩阵：
(55)
对矩阵进行量纲一化处理：
(56)
得到求差矩阵：
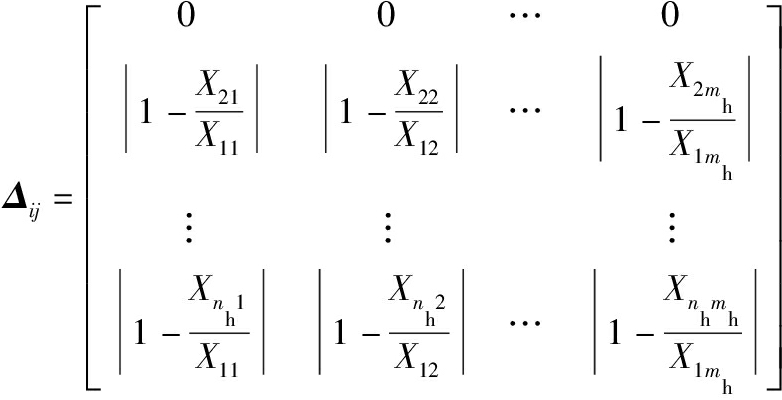
(57)
计算关联系数：
(58)
式中，Δmax、Δmin分别为Δij矩阵中的最大、最小值；αg为分辨系数，一般取0.5。
求灰色关联度γi：
(59)
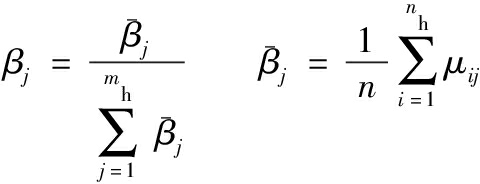
灰色关联度γi的值越大说明第i个解的效果越好。利用灰色关联分析法对INSGSA算法求得的Pareto解集进行选择决策，部分结果如表9所示，得到算法的解集中灰色关联度γi最大值为0.84，切削参数(vc,fz,ae)=(16.25,0.82,31.64)，选择该组参数组合进行铣削加工可达到较好的优化效果。
表9 INSGSA算法处理铣削加工多目标优化问题部分Pareto最优解及其灰色关联度
Tab.9 Pareto optimal solution and gray correlation of multi-objective optimization problem in milling processing with INSGSA algorithm
铣削参数(vc,fz,ae)优化目标(Tave,SCE,SPC)灰色关联度γi(16.25,0.82,31.64)(3.22,3.49×10-6,1.49×10-3)0.84(17.26,0.49,46.03)(3.35,3.58×10-6,1.47×10-3)0.81(23.39,0.82,31.71)(2.79,3.98×10-6,1.60×10-3)0.77(44.64,0.49,46.00)(2.44,6.27×10-6,2.10×10-3)0.62(31.42,0.61,39.10)(2.61,4.66×10-6,1.74×10-3)0.70(36.16,0.59,40.17)(2.53,5.28×10-3,1.88×10-3)0.66(35.31,0.49,46.00)(2.57,4.88×10-3,1.78×10-3)0.69
4 结论
本文针对铣削加工中存在的高成本、高碳排放和低效率问题，以最小单位体积生产成本、最小体积单位碳排放和最小生产时间为优化目标，在实际生产环境的多种约束下，建立了铣削加工过程多目标优化模型。根据Pareto最优原理，在NSGSA算法的基础上，对该算法存在的缺陷进行改进，提出了改进的非支配排序引力搜索算法，算法采用精英保留策略和位置更新回退操作引导群体质点向真实Pareto最优解集区域靠近，提出了精英-精英交叉策略和精英-非精英交叉策略，增加了群体多样性，使算法在处理多目标优化问题时具有更好的寻优能力，获得更加接近Pareto-真实前端的Pareto解集。借助于该改进算法，决策人员可根据优先优化目标灵活选择相应的铣削参数进行加工，该改进算法可为决策人员提供灵活的、适用于各种不同场景的选择。
[1] MENG Leilei,ZHANG Chaoyong,SHAO Xinyu, et al.Mathematical Modelling and Optimisation of Energy-conscious Hybrid Flow Shop Scheduling Problem with Unrelated Parallel Machines[J].International Journal of Production Research,2019,57(4)：1119-1145.
[2] 孟磊磊，张超勇，肖华军，等.面向加工时间可控的柔性作业车间节能调度问题建模研究[J].计算机集成制造系统，2019，25(5)：1062-1074.
MENG Leilei, ZHANG Chaoyong, XIAO Huajun,et al.Mathematical Modeling of Energy-efficient Flexible Job Shop Scheduling Problem with Controllable Processing Times[J].Computer Integrated Manufacturing Systems, 2019，25(5)：1062-1074.
[3] ASOKAN P, SARAVANAN R, VIJAYAKUMAR K.Machining Parameters Optimisation for Turning Cylindrical Stock into a Continuous Finished Profile Using Genetic Algorithm(GA)and Simulated Annealing(SA)[J].International Journal of Advanced Manufacturing Technology,2003,21:1-9.
[4] 刘海江, 黄炜.基于粒子群算法的数控加工切削参数优化[J].同济大学学报(自然科学版), 2008, 36(6):803-806.
LIU Haijiang,HUANG Wei.Computer Numerical Control Machining Parameter Optimization Based on Particle Swarm Optimization[J].Journal of Tongji University(Natural Science), 2008, 36(6):803-806.
[5] YILDIZ A R.Optimization of Multi-pass Turning Operations Using Hybrid Teaching Learning-based Approach[J].International Journal of Advanced Manufacturing Technology, 2013, 66:1319-1326.
[6] MENG Leilei,ZHANG Chaoyong,SHAO Xinyu, et al.MILP Models for Energy-aware Flexible Job Shop Scheduling Problem[J].Journal of Cleaner Production,2019,210:710-723.
[7] RAJEMI M F, MATIVENGA P T, ARAMCHAROEN A.Sustainable Machining:Selection of Optimum Turning Conditions Based on Minimum Energy Considerations[J].Journal of Cleaner Production, 2010, 18(10/11):1059-1065.
[8] 李聪波, 崔龙国, 刘飞,等.面向高效低碳的数控加工参数多目标优化模型[J].机械工程学报, 2013,49(9):87-96.
LI Congbo, CUI Longguo, LIU Fei,et al.Multi-objective NC Machining Parameters Optimization Model for High Efficiency and Low Carbon[J].Journal of Mechanical Engineering, 2013,49(9):87-96.
[9] YAN Jihong,LI Lin.Multi-objective Optimization of Milling Parameters：the Trade-offs between Energy, Production Rate and Cutting Quality[J].Journal of Cleaner Production,2013,52:462-471.
[10] HANAFI I, KHAMLICHI A,CABRERA F M, et al.Optimization of Cutting Conditions for Sustainable Machining of PEEK-CF30 Using TiNTools[J].Journal of Cleaner Production, 2012, 33:1-9.
[11] LIU C G, YANG J, LIAN J, et al.Sustainable Performance Oriented Operational Decision-making of Single Machine Systems with Deterministic Product Arrival Time[J].Journal of Cleaner Production, 2014, 85:318-330.
[12] 黄拯滔.面向低碳制造的数控铣削过程建模与参数优化研究[M].武汉：华中科技大学,2016.
HUANG Zhengtao.Research on Modeling and Cutting Parameters Optimization of CNC Milling Process for Low-carbon Manufacturing[M].Wuhan：Huazhong University of Science and Technology, 2016.
[13] 李聪波,崔龙国,刘飞,等.基于广义边界的机械加工系统碳排放量化方法[J].计算机集成制造系统,2013,19(9):2229-2236.
LI Congbo, CUI Longguo, LIU Fei,et al.Carbon Emissions Quantitative Method of Machining System Based on Generalized Boundary[J].Computer Integrated Manufacturing Systems, 2013,19(9):2229-2236.
[14] RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S.GSA:a Gravitational Search Algorithm[J].Information Sciences,2009,179(13):2232-2248.
[15] 刘勇，马良.非线性极大极小问题的混沌万有引力搜索算法求解[J].计算机应用研究，2012，29(1)：47-48.
LIU Yong, MA Liang.Solving Nonlinear Minimax Problems Based on Chaos Gravitational Search Algorithm[J].Application Research of Computers, 2012, 29(1):47-48.
[16] NOBAHARI H, NIKUSOKHAN M, SIARRY P.A Multi-objective Gravitational Search Algorithm Based on Non-dominated Sorting[J].International Journal of Swarm Intelligence Research(IJSIR), 2012, 3(3):32-49.
[17] SÖNMEZA I, 
A, DERELI T, et al.Dynamic Optimization of Multi-pass Milling Operations via Geometric Programming[J].International Journal of Machine Tools and Manufacture, 1999, 39(2):297-320.
[18] ZOU F, WANG L, HEI X, et al.Multi-objective Optimization Using Teaching-learning-based Optimization Algorithm[J].Engineering Applications of Artificial Intelligence, 2013, 26(4):1291-1300.
