0 引言
数控机床可靠性试验是反映机床稳定高效生产能力的重要方法,试验中需对主轴施加多维力载荷以模拟机床加工时的载荷环境。现有方法是通过长时间切削加工对主轴施加切削力,但是,该方法会消耗大量刀具和工件材料,测试成本高,不利于可靠性试验的可持续发展。由此,需要研制一种多维力加载装置,模拟机床主轴所处的切削力环境,为可靠性试验提供一种低成本、可循环的绿色加载方法,有利于可靠性试验的标准化和规模化开展。
要模拟机床加工时主轴的切削力环境,加载装置需实现3个功能:第一,加载装置装于机床工作台上,连接主轴并跟随主轴的多轴联动进给运动;第二,在跟随过程中,加载装置需对主轴施加三维力,形成进给抗力,作为模拟切削力的基础;第三,根据实际载荷谱设定加载指令,实现变载荷周期性动态加载,真实模拟切削力环境。由于目前针对机床多维力加载装置的相关研究比较少见,所以本文首先从第一点和第二点出发,研究针对多轴联动进给主轴的多维力随动加载装置,作为切削力模拟的基础,后续将开展变载荷动态加载研究。
目前,已有学者对运动目标的随动加载开展研究。NAM[1]采用电液伺服机构对飞行器控制面进行了地面载荷模拟。TRUONG等[2]设计了模糊PID力控制算法,可对一维直线运动目标施加同轴力。SHANG等[3]和LI等[4]研制了电液伺服负载模拟器,可跟随电机输出轴的转动同时加载同轴的转矩,模拟飞行器伺服机构在飞行中所承受的气动载荷,并从摩擦力矩、多余力矩等方面提高加载性能。尚耀星等[5]发明了一种弯扭组合时变载荷加载装置。在机床测试领域,杨兆军等[6-7]研制了电主轴可靠性试验台,在主轴转动时对其施加径向力、轴向力和扭矩。国家机床质量监督检验中心采用气动作动器对执行一维进给运动的主轴实时跟随并施加同向力。然而,上述研究中加载目标多进行一维运动,未实现对三维空间运动目标的随动加载,而且不具备三维力加载能力,不利于五轴联动机床的切削力模拟。
为解决加载维度不足的问题,有学者提出使用并联机构进行多维力加载的办法。并联机构结构紧凑、刚度高、动态性能好,具备在机床中进行加载的可行性。WALKER等[8]和STOKES等[9]基于六自由度并联机构对脊柱关节进行了多维力学性能测试。NIERENBERGER等[10]和CARPIUC-PRISACARI等[11]在Stewart-Gough并联平台上分别进行了Nooru-Mohamed缺口混凝土试验及混合型裂纹扩展试验,进行拉力、剪力和弯矩组合加载。GUO等[12]基于6-UPS并联机构研制多维力加载材料试验机,对材料试件施加六维力载荷,用于测试复杂载荷下的材料力学性能。然而,上述研究仅对静态目标进行多维力加载,尚未开展运动目标的多维力加载研究,并且未应用于机床测试领域。
笔者所在课题组基于并联机构提出多维力随动加载装置,该装置在跟随机床主轴三轴联动进给运动的同时对其施加三维力[13-14]。但是,该研究是在机床实验平台上开展的,鉴于真实机床与实验平台的结构差异较大,仍需进一步在真实机床上开展多维力加载实验验证,同时已有研究内容仅针对三轴联动机床,尚未涉及五轴联动机床的加载研究。
本文以提高跟随进给运动和加载力的维度为出发点,研制多维力随动加载装置,该装置可跟随机床主轴的五轴联动进给轨迹并对主轴施加三维恒力,形成复杂进给抗力,作为模拟五轴机床切削力环境的基础。本文可解决机床可靠性试验中依靠长期加工进行加载的局限,提供一种低成本、可循环的多维力加载方法。同时,在真实的五轴联动机床上验证了多维力随动加载的可行性,为机床可靠性试验提供一种有效的切削力模拟装置和方法。
1 多维力随动加载装置理论分析
1.1 几何参数与坐标系定义
多维力随动加载装置基于6-PUS并联机构研制,由静平台、动平台和6条驱动支链组成,结构和几何参数如图1所示。运动支链包括直线驱动、虎克铰、定长连杆和复合球铰,两端分别通过直线驱动和复合球铰连接静平台和动平台。
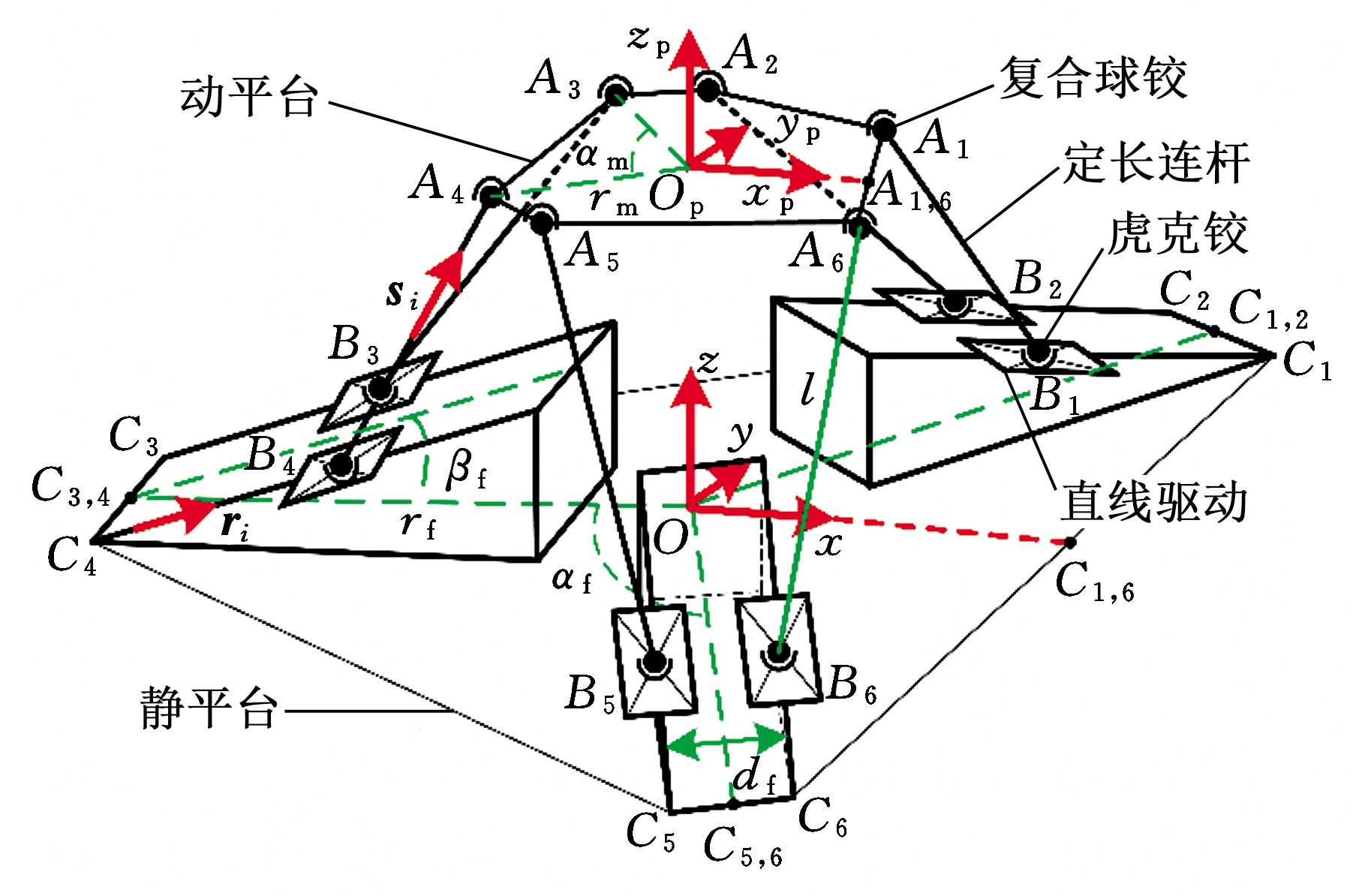
图1 几何参数与坐标系示意图
Fig.1 Geometric parameters and coordinate definition
图1中,使用i(i=1,2,…,6)标记6条支链,Ai与Bi分别表示复合球铰和虎克铰的转动中心,Ci表示驱动滑块在初始位置时虎克铰的转动中心。6个直线驱动分为3组安装于3个沿圆周均布的斜面上,斜面倾角记为βf,各组使用j(j=1,2,3)标记,C2j-1,2j为每组C2j-1和C2j的中点,分布在半径为rf的圆上,圆心为O,相邻的两组中线OC2j-1,2j夹角记为αf。B2j-1C2j-1与B2jC2j平行,间距为df。动平台上Ai同样分为3组均布于半径为rm的圆上,圆心为Op,各组同样用j表示,αm表示∠A2j-1OpA2j。定长连杆BiAi的方向向量为si,长度为l。各几何参数、含义及其数值详见表1。
表1 加载装置几何参数
Tab.1 Geometric parameters of the loading device

参数含义数值rm(mm)Ai所在圆的半径值100αm(°)∠A2j-1OpA2j80rf(mm)C2j-1,2j所在圆的半径值319αf(°)∠C2j-1OpC2j120βf(°)斜面倾斜角度30df(mm)B2j-1C2j-1 与 B2jC2j 之间距离146l(mm)定长连杆BiAi长度340
在静平台中心O点建立静坐标系Oxyz,其x轴指向C1,6,z轴垂直于静平台平面指向动平台方向,y轴根据右手定则获得。在动平台中心Op建立动坐标系Opxpypzp,xp轴正方向指向线段A1A6中点A1,6,zp轴垂直于动平台平面,yp轴由右手定则得出。
1.2 运动学逆解
运动学逆解是指通过给定动平台位姿,计算各支链中直线驱动的位移量的过程。支链i可形成运动闭环OCiBiAiOpO,利用封闭矢量法描述该闭环为
T(x,y,z)+R(γ,β,α) pai=ci+diri+lisi
(1)
式中,T(x,y,z)=OOp,为坐标系的位置向量;R(γ,β,α)为动坐标系的姿态矩阵;pai为向量OpAi在动坐标系中的表示;ci=OCi;diri=CiBi,如图1所示,di和ri分别为移动副CiBi的位移量和方向向量;lisi=BiAi=li,li和si分别为定长连杆向量BiAi的长度和方向向量。
令hi=T(x,y,z)+R(γ,β,α) pai-ci,可求解各支链驱动量为
(2)
1.3 运动学正解
运动学正解是指已知直线驱动的位移向量d=(d1,d2,…,d6)T,求解动平台位姿向量xp=(TT,ΘT)T的过程,其中Θ=(θx,θy,θz)T,为动平台的姿态向量。动平台姿态向量Θ与旋转矩阵R可相互转化,采用四元数A(A=(a0,a1,a2,a3)T)表示动平台姿态可有效减小旋转矩阵的计算复杂程度,使计算更快速稳定。构造如下关于位姿向量Q=(TT,AT)T的方程组:
![]()
(3)
(4)
其中,式(3)可由式(1)推出,式(4)是单位四元数的约束方程。采用牛顿迭代法[15]即可获得Q的数值解,求解过程如图2所示。

图2 牛顿迭代法求解流程图
Fig.2 The flowchart of Newton-Raphson method
2 控制系统设计
模拟数控机床在加工时的切削力环境需依照期望载荷指令驱动加载装置对运动主轴持续施加多维力,所以,需要设计多维力加载控制系统,根据加载装置的力反馈信息,实时调节驱动量,以实现快速、稳定的多维力随动加载,控制系统框图见图3。

图3 多维力控制系统框图
Fig.3 The overall multi-axis force control system
在给定期望加载力向量Fr后,通过基于虚功原理[16]建立的动力学模型可以计算支链期望加载力向量fr。驱动位移向量d由集成在直线驱动的光栅尺测出,并由此计算速度和加速度向量。动平台位姿向量xp及其速度、加速度向量可通过运动学正解计算。
各支链采取基于模糊PID的力控制方法[14],根据加载误差ei及其变化率,实时调节控制器的增益,计算控制分量UPID,实现对加载误差快速、稳定地修正。另外,引入力前馈和速度前馈用于消除控制系统滞后。通过期望力和变化率形成力前馈控制分量Uff,通过速度形成速度前馈控制量Uvf。最终,将3个控制量相加,即可构成用于控制支链i的控制总量:
(5)
3 多维力随动加载实验
基于6-PUS并联机构研制多维力随动加载装置样机,如图4所示。加载装置静平台上装有6个线性模组用作直线驱动,可将伺服电机的旋转运动转化为其滑块的直线运动,滑块位移通过集成的光栅尺反馈。滑块上依次安装了虎克铰、定长连杆、力传感器和复合球铰,最终与动平台相连。改变线性模组的滑块位移即可驱动动平台进行空间六自由度运动。加载装置可沿自身X、Y和Z轴平移±100 mm,最大速度为100 mm/s;可绕X、Y和Z轴旋转±30°,最大角速度为30°/s。同时,加载装置可输出时变周期性载荷,具备1 000 N的力加载和10 N·m的力矩加载能力,沿三轴目前可实现幅值250 N、频率0.2 Hz的周期力加载。

图4 多维力随动加载装置样机
Fig.4 Prototype of the multi-axis loading device
多维力随动加载实验主要考察使用并联机构同时实现跟随五轴联动进给和对主轴加载的可行性,验证控制系统的有效性,评估加载装置模拟机床在加工时所遇进给抗力的能力。在加载实验中,设定机床主轴的转速为0,仅驱动主轴执行由X、Y、Z轴平移和A、C轴旋转组成的五轴联动进给运动,加载装置需在跟随主轴运动的同时对其施加三维力,模拟铣削过程中的三维切削力。
多维力随动加载实验在Mikron WF-74 ch五轴联动数控机床上开展,实验现场如图4所示。加载装置静平台安装在机床工作台上,动平台通过主轴连接器与机床主轴连接。主轴连接器包括连接法兰、弱刚性杆和刀柄锥度轴三部分,其中连接法兰和刀柄锥度轴分别用于连接动平台和机床主轴,弱刚性杆起缓冲过渡的作用,降低加载时的冲击。在加载时,先通过夹刀程序使主轴夹紧刀柄锥度轴,随后驱动动平台相对机床主轴产生位移,致使弱刚性杆发生弹性形变,从而对主轴形成加载力。此连接器仅能用于主轴转速为0的加载实验,若转速不为0则需重新设计连接器,此部分工作目前正在进行,相关研究将在后续论文中报道。
在多维力随动加载实验中,机床主轴保持静止,仅执行五轴联动进给运动。根据机床主轴进给运动种类,随动加载可分为4类,分别是针对单轴移动进给的随动加载、针对三轴联动进给的随动加载、针对单轴回转进给的随动加载以及针对五轴联动进给的随动加载。加载装置在跟随主轴进给运动的同时,需要根据多维加载力向量Fr=(Fx,Fy,Fz),对主轴施加三维力载荷,模拟铣削时主轴所受切削力环境,其中Fx、Fy、Fz分别是沿X、Y、Z轴的期望力。已有研究实现了通过气缸对单轴移动进给主轴施加同轴一维恒力,由于本实验需跟随更复杂的五轴联动进给轨迹并施加三维力,所以期望力首先采用恒力形式,在加载装置输出力范围内选取正负各异的期望值,评价加载装置对进给主轴的随动加载能力,以此作为切削力模拟的基础。
3.1 针对单轴移动进给主轴的随动加载实验
设置机床主轴相对工作台分别沿X、Y、Z轴做匀速直线运动,速度分别设定为1 mm/s、1 mm/s和0.5 mm/s。定义期望加载力Fr=(300 N, -300 N, 500 N),即沿X轴施加300 N恒力,沿Y轴施加-300 N恒力,沿Z轴施加500 N恒力。利用加载装置的力传感器实时反馈实际多维加载力,加载力曲线及各分力的加载误差曲线见图5。
从实验结果可以看出,实际加载力分布于期望值附近,说明加载装置可以实时跟随机床主轴的单轴移动进给运动,同时对主轴施加三维力。稳定加载阶段在图5中用虚线框标出,加载误差的均值、标准差和最大值详见表2。
3个实验中沿X、Y、Z轴的加载误差均值分别小于0.30 N、0.74 N和3.78 N,标准差分别小于1.58 N、1.95 N和7.12 N。最大加载误差均不超过期望加载力的2.2%,具有较好的加载精度。
3.2 针对三轴联动进给主轴的随动加载实验
设置机床主轴执行三轴联动进给运动,相对工作台沿空间直线做匀速直线运动,沿X、Y、Z轴速度均为1 mm/s。定义期望加载力为Fr =(300 N, -300 N, 500 N)。实际加载力与加载误差如图6所示,加载误差均值、标准差和最大值如表3所示。
由图6可知,当主轴进行三轴联动进给运动时,加载装置能够跟随主轴运动并按照期望值对主轴施加三维力。稳定加载时,沿X、Y、Z轴的加载误差均值分别为-1.71 N、1.68 N、-7.61 N,标准差分别为1.29 N、2.37 N、7.42 N,最大相对误差均不超过期望值的3.2%,加载精度较好。

(a)沿X轴进给
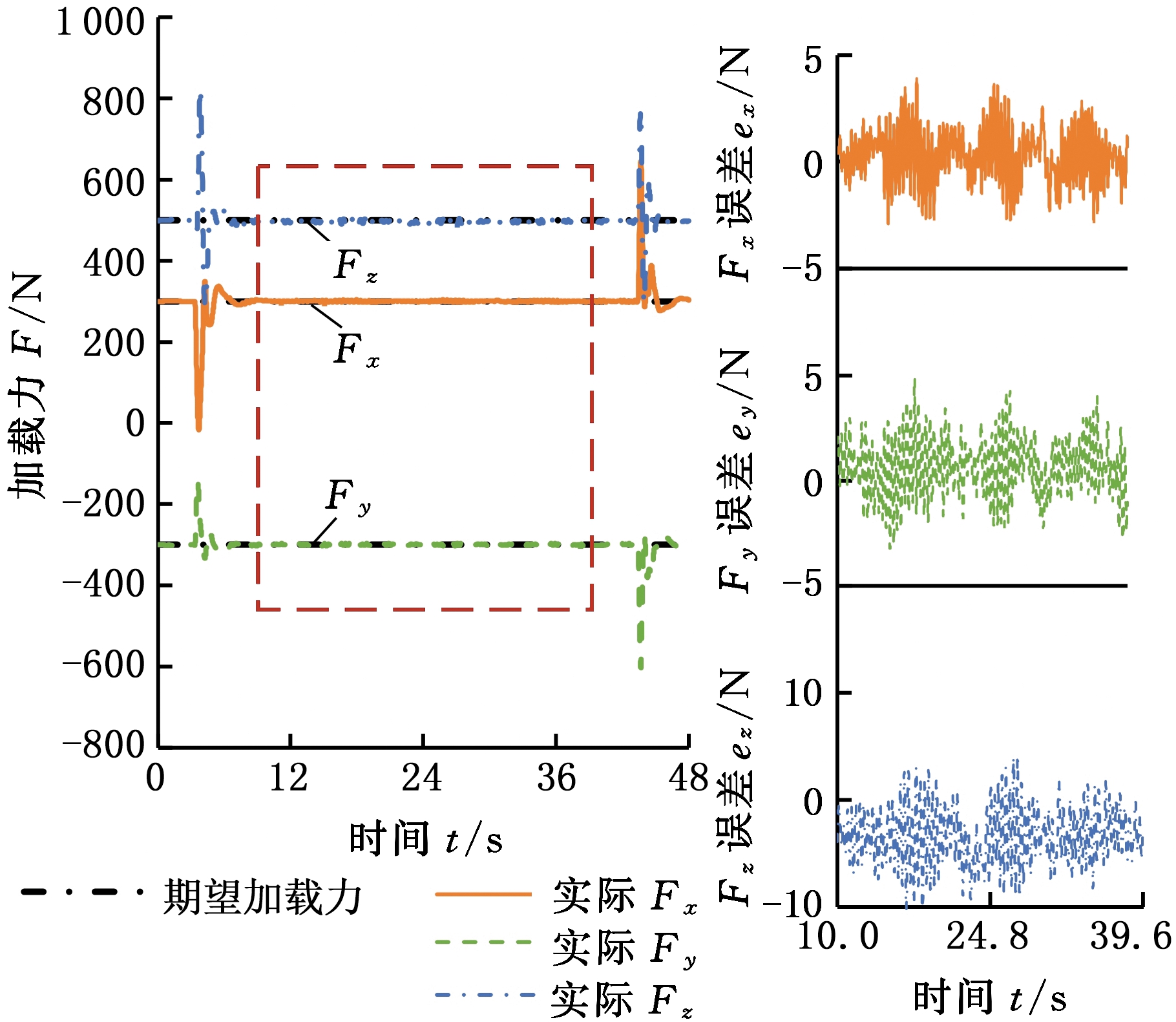
(b)沿Y轴进给
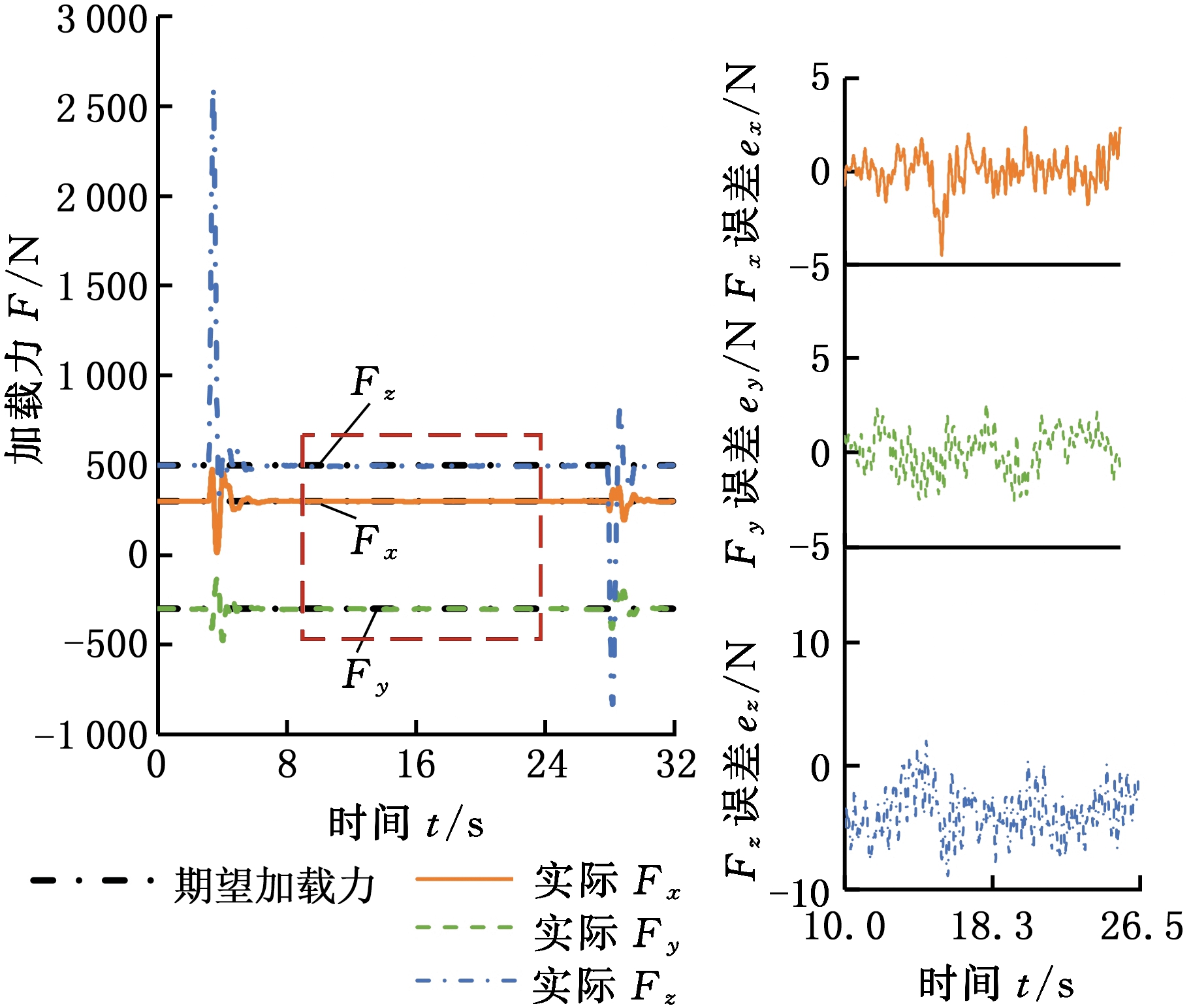
(c)沿Z轴进给
图5 单轴移动进给主轴的随动加载实验结果
Fig.5 The results of load-while-track experiments for the spindle performing uniaxial translational feeding
3.3 针对单轴回转进给主轴的随动加载实验
设置机床工作台分别绕A轴与C轴匀速转动,转动速度均为0.5 °/s,期望加载力定义为Fr =(300 N, -300 N, 500 N),实际加载力和加载误差如图7所示,稳定加载阶段的加载误差均值、标准差和最大值见表4。
表2 单轴移动进给主轴的随动加载误差
Tab.2 Loading errors for the spindle performing uniaxialtranslational feeding

加载误差沿X轴移动沿Y轴移动沿Z轴移动FxFyFzFxFyFzFxFyFz均值(N)-0.23-0.74-3.550.300.67-3.390.040.09-3.78标准差(N)0.721.153.761.581.957.120.951.113.75最大值(N)2.443.889.233.924.8810.604.502.628.87最大相对误差0.81%1.29%1.85%1.31%1.63%2.12%1.5%0.87%1.77%

图6 三轴联动进给主轴的随动加载实验结果
Fig.6 The result of load-while-track experiment for the spindle performing 3-axis translational feeding
表3 三轴联动进给主轴的随动加载误差
Tab.3 Loading errors for the spindle performing3-axis translational feeding

加载误差三轴联动FxFyFz均值(N)-1.711.68-7.61标准差(N)1.292.377.42最大值(N)5.486.6515.66最大相对误差1.82%2.22%3.13%
从实验结果可以看出,加载装置可实时跟随工作台的单轴回转进给运动,并同时对主轴施加三维力。沿X、Y、Z轴加载误差的均值分别不超过0.75 N、2.05 N、-4.71 N,标准差分别不超过1.32 N、2.42 N、5.67 N,最大误差为4.43 N、6.48 N、10.83 N,均未超过期望值的2.2%,加载精度较好。
3.4 针对五轴联动进给主轴的随动加载实验
设置机床主轴执行五轴联动进给运动,主轴相对工作台沿空间直线匀速运动,工作台执行二自由度匀速转动。主轴沿X、Y、Z轴速度分别为-0.53 mm/s、-0.53 mm/s、0.13 mm/s,工作台绕A轴、C轴的转动速度分别为0.08°/s,-0.13°/s。
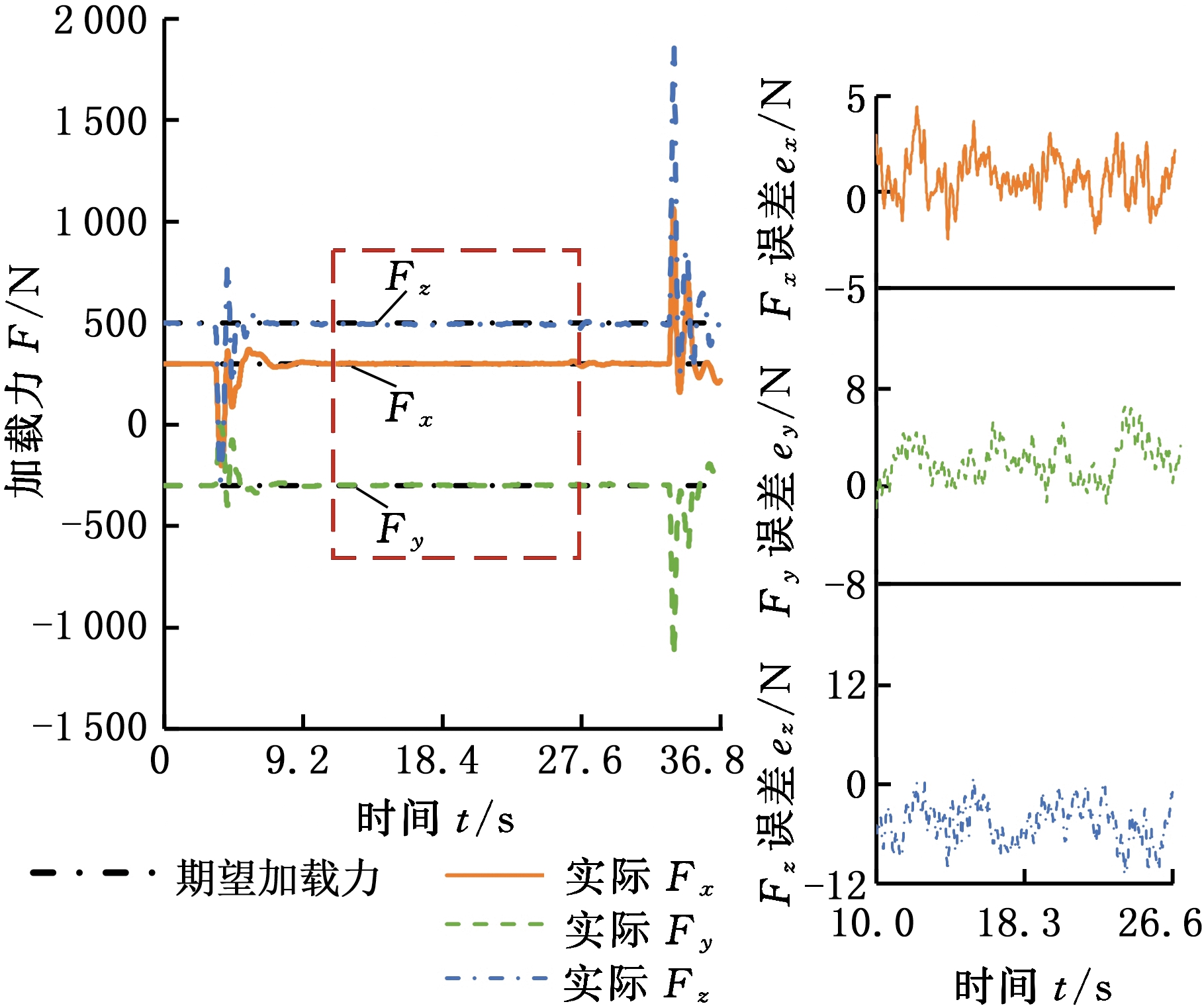
(a)绕A轴进给
(b)绕C轴进给
图7 单轴转动进给主轴的随动加载实验结果
Fig.7 The results of load-while-track experiments for the spindle performing uniaxial rotational feeding
表4 单轴回转进给主轴的随动加载误差
Tab.4 Loading errors for the spindle performing uniaxialrotational feeding

加载误差绕A轴转动绕C轴转动FxFyFzFxFyFz均值(N)0.752.05-4.71-0.17-0.39-1.55标准差(N)1.322.425.670.570.781.40最大值(N)4.436.4810.832.352.384.55最大相对误差1.48%2.16%2.17%0.78%0.79%0.91%
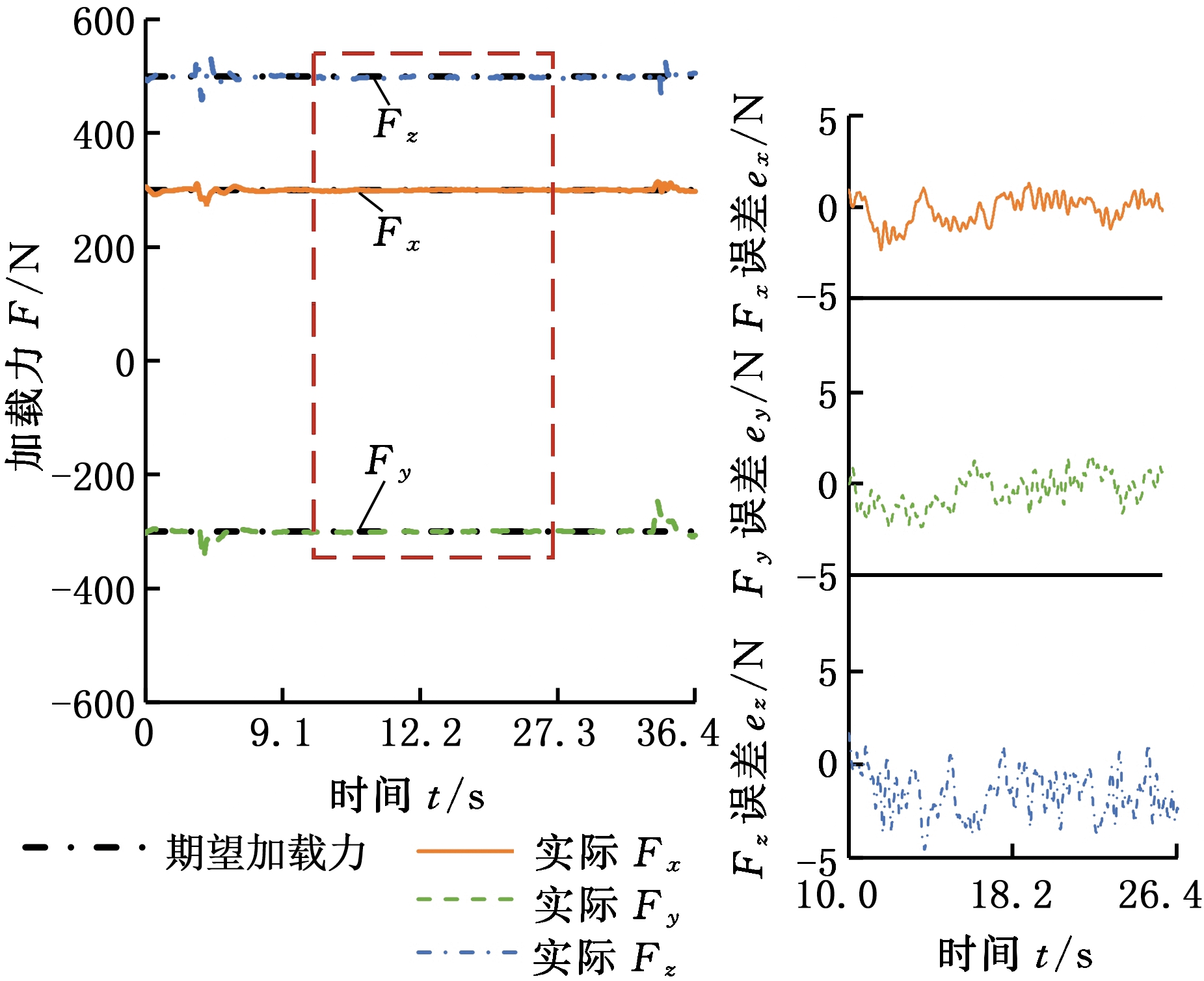
定义期望加载力Fr=(-300 N, 300 N, 500 N)。实际加载力及加载误差如图8所示,表5汇总了稳定加载时的加载误差均值、标准差和最大值。

图8 五轴联动进给主轴的随动加载实验结果
Fig.8 The result of load-while-track experiment for the spindle performing 5-axis feeding
从图8中可以看出,加载装置可以根据期望值对执行五轴联动进给运动的机床主轴施加三维力。稳定加载时,沿X、Y、Z轴加载误差的均值分别为-1.71 N、1.68 N和-7.61 N,标准差分别为1.29 N、2.37 N和7.42 N,并且最大加载误差均不超过期望值的1.3%,具备较好的加载精度。
表5 五轴联动进给主轴的随动加载误差
Tab.5 Loading errors for the spindle performing5-axis feeding
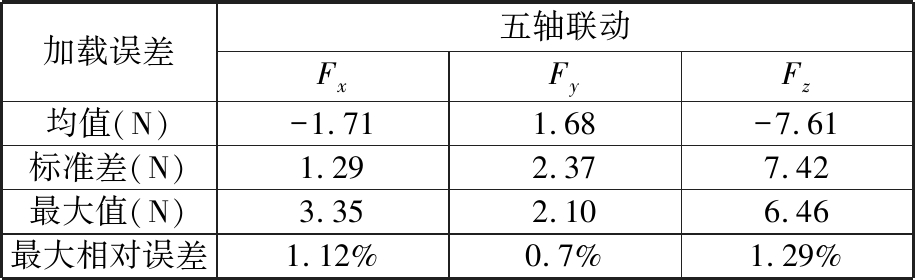
加载误差五轴联动FxFyFz均值(N)-1.711.68-7.61标准差(N)1.292.377.42最大值(N)3.352.106.46最大相对误差1.12%0.7%1.29%
观察图5至图8可以发现,在主轴开始和结束进给运动时,实际加载力均存在较大的扰动。这是由于主轴启停的加速度较大,受控制系统的实时性约束,加载装置响应不及时,对实际加载力产生较大扰动,但控制系统可较快纠正偏差并将加载力收敛至期望值附近,证明控制系统具备较好的稳定性。
沿Z轴加载误差的均值、标准差和最大值均大于沿X、Y轴的加载误差,这是因为主轴连接器和加载装置沿Z轴方向的刚度较大,相同位移会产生更大的接触力,对实际加载力的影响更显著。
实验结果表明,本文提出的多维力随动加载装置可以实时跟随五轴联动数控机床主轴的单轴、三轴联动和五轴联动进给运动,并同时根据期望值对主轴施加三维力载荷,加载精度较好,最大加载误差均小于期望值的3.2%,可对机床提供多轴进给抗力,并为通过动态加载提升切削力模拟的准确性提供理论和装备支撑。
4 结论与展望
(1)基于模糊PID的显式力控制算法可驱动并联机构对多自由度运动目标施加多维力载荷。
(2)多维力随动加载装置可对执行五轴联动进给运动的机床主轴施加三维力载荷,加载精度较好,误差小于期望值的3.2%,有效模拟机床在执行多种加工轨迹时的平均切削力。
(3)在真实的五轴联动数控机床上开展多维力随动加载实验,验证随动加载的可行性,形成复杂切削力模拟的研究基础,为数控机床可靠性试验提供低成本、可循环的加载手段,避免长期切削加载造成的材料损耗,有利于机床可靠性测试的规模化和标准化发展。
(4)目前在切削力模拟方面的研究报道仍少见,本文对五轴联动进给主轴的多维力随动加载开展初步研究,实验中的主轴进给速度相对较低且加载恒力,主要用于验证随动加载的可行性,形成切削力模拟的研究基础。未来研究将集中于动态特性更优的控制系统设计,适应对旋转主轴的周期性加载需求。同时,开展变载荷动态加载,更接近实际切削力工况。本文也为机床精度保持性测试、超载试验、跑合试验等性能测试提供新的负载模拟装置和方法。
[1] NAM Y.QFT Force Loop Design for the Aerodynamic Load Simulator [J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(4): 1384-1392.
[2] TRUONG D Q, AHN K K. Force Control for Hydraulic Load Simulator Using Self-tuning Grey Predictor-fuzzy PID [J]. Mechatronics, 2009, 19(2): 233-246.
[3] SHANG Yaoxing, JIAO Zongxia, WANG Xiaodong, et al. Study on Friction Torque Loading with an Electro-hydraulic Load Simulator[J]. Chinese Journal of Aeronautics, 2009, 22(6): 691-699.
[4] LI Zhihui, SHANG Yaoxing, JIAO Zongxia. Surplus Torque Elimination Control of Electro-hydraulic Load Simulator Based on Actuator Velocity Input Feedforword Compensating Method[J]. Journal of Dynamic Systems, Measurement, and Control, 2018, 140(10): 101001.
[5] 尚耀星, 焦宗夏, 王晓东, 等. 一种弯扭组合二维时变载荷加载装置:CN101441477B[P]. 2011-01-12.
SHANG Yaoxing, JIAO Zongxia, WANG Xiaodong, et al. A Loading Device with 2-DOF Time-varying Bending-torsion Combined Loading Capacity: CN101441477B[P]. 2011-01-12.
[6] 呼烨,杨兆军,宋靖安,等. 基于电力测功和压电陶瓷加载系统的高速电主轴可靠性试验台设计[J]. 科技导报, 2012, 30(1): 34-38.
HU Ye, YANG Zhaojun, SONG Jing’an, et al. Design of a Reliability Test Platform for High-speed Motorized Spindles Based on Power Dynamometer and Piezoelectric Loading Systems[J]. Science and Technology Review, 2012, 30(1): 34-38.
[7] 邱荣华, 刘宏昭. 高速电主轴非接触电磁加载装置设计与实现[J]. 中国机械工程, 2014, 25(8): 1027-1032.
QIU Ronghua, LIU Hongzhao. Design and Implementation of High Speed Motorized Spindle’s Non-contact Electromagnetic Loading System[J]. China Mechanical Engineering, 2014, 25(8): 1027-1032.[8] WALKER M R, DICKEY J P. New Methodology for Multi-dimensional Spinal Joint Testing with a Parallel Robot[J]. Medical & Biological Engineering & Computing, 2007, 45(3): 297-304.
[9] STOKES I A, MACK G M, DAVID C, et al. Measurement of a Spinal Motion Segment Stiffness Matrix[J]. Journal of Biomechanics 2002, 35(4): 517-521.
[10] NIERENBERGER M, PONCELET M, PATTOFATTO S, et al.Multiaxial Testing of Materials Using a Stewart Platform: Case Study of the Nooru-mohamed Test[J]. Experimental Techniques, 2014, 38(2): 74-83.
[11] CARPIUC-PRISACARI A, PONCELET M, KAZYMYRENKO K, et al.A Complex Mixed-mode Crack Propagation Test Performed with a 6-axis Testing Machine and Full-field Measurements [J]. Engineering Fracture Mechanics, 2017, 176: 1-22.
[12] GUO Jiangzhen, WANG Dan, FAN Rui, et al. Development of a Material Testing Machine with Multi-dimensional Loading Capability[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2016, 10(2): M17.
[13] GUO Jiangzhen, WANG Dan, LI Tian, et al. Triaxial Loading Device for Reliability Tests of Three-axis Machine Tools[J]. Robotics and Computer-integrated Manufacturing, 2018, 49: 398-407.
[14] GUO Jiangzhen, WANG Dan, CHEN Wuyi, et al. Multiaxis Loading Device for Reliability Tests of Machine Tools[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(4): 1930-1940.
[15] ZHOU Wanyong, CHEN Wuyi, LIU Huadong, et al. A New Forward Kinematic Algorithm for a General Stewart Platform[J]. Mechanism and Machine Theory, 2015, 87: 177-190.
[16] TSAI L W. Solving the Inverse Dynamics of a Stewart-gough Manipulator by the Principle of Virtual Work[J]. Journal of Mechanical Design, 2000, 122(1): 3-9.
