0 引言
磁流变减振器具有在通电磁场下改变阻尼系数的功能,且其动态可调范围大、响应速度快、功率要求低,因此,安装了磁流变减振器的半主动悬架逐渐成为研究热点。磁流变悬架控制器根据半主动控制策略计算出所需的阻尼力,通过磁流变减振器逆模型得到控制电流,实现对减振器的控制。在建立这种高度非线性逆模型之前,需要对磁流变减振器的正向动力学特性进行较高精度的建模。通过建立面向控制且精确的磁流变减振器正逆动力学模型,密切跟踪半主动悬架控制策略得出的期望阻尼力,才能尽可能实现磁流变半主动悬架理想的控制效果。
正向模型表征磁流变减振器的非线性滞回特性,根据激励电流和活塞相对运动状态来计算输出阻尼力。国内外研究人员提出了多种正向模型,如目前广泛应用于描述磁流变减振器滞回特性的Bouc-Wen模型[1-3]和基于动力学的LuGre模型等。Bouc-Wen滞回算子最先是由BOUC[4]在分析描述平滑滞回模型时提出的,之后WEN[5]对其进行了改进和推广。SPENCER等[6]采用Bouc-Wen滞回算子描述磁流变减振器的滞回特性。但在速度绝对值较小、速度与加速度符号相反的阻尼力-速度特性区域,Bouc-Wen模型不能很好地描述该区域的阻尼力衰减特性。CANUDAS-DE-WIT等[7]、LISCHINSKY等[8]提出了可用于描述摩擦系统的LuGre动力学模型。JIMNEZ等[9-10]提出了修正的磁流变减振器LuGre模型。为了便于建立磁流变减振器逆模型,SAKAI等[11]进一步修改了LuGre模型。然而,在零速度区域附近,实验数据和LuGre模型响应之间存在较大误差。
磁流变减振器逆模型往往需要在正模型的基础上进行建模,根据控制算法所得的期望阻尼力和活塞相对运动状态计算控制电流。TSANG等[12]对Bouc-Wen模型作了适当简化,提出了一种逆向动力学模型的建模方法,釆用指数函数的形式来描述屈服阻尼力与控制电流的关系,由此得到控制电流的解析解。BAHAR等[13]提出了另一种简化方法,将模型中的部分变量简化为与速度相关的符号函数。上述两个简化过程虽然易于逆向建模,但都忽略了阻尼器的滞回效应,导致低速时的预测电流精度较差。SAKAI等[11]简化了LuGre模型中相关变量与输入电流之间的关系,得到了磁流变阻尼器逆模型的解析解,该逆模型在低速时对控制电流的预测具有较高的计算精度,但内部变量的求逆过程较为困难。
薛兵等[14]提出用魔术公式描述磁流变减振器运动过程中产生的剪切及屈服应力的剪切项,建立了磁流变减振器滞回特性魔术公式模型。该模型形式简单、参数一致且参数物理意义明确,方便用于半主动悬架系统动力学分析与控制器开发。本文基于磁流变减振器滞回特性魔术公式,进一步提出磁流变减振器魔术公式逆模型,并应用于1/4车辆磁流变半主动悬架系统仿真及台架实验中。
1 磁流变减振器魔术公式模型介绍
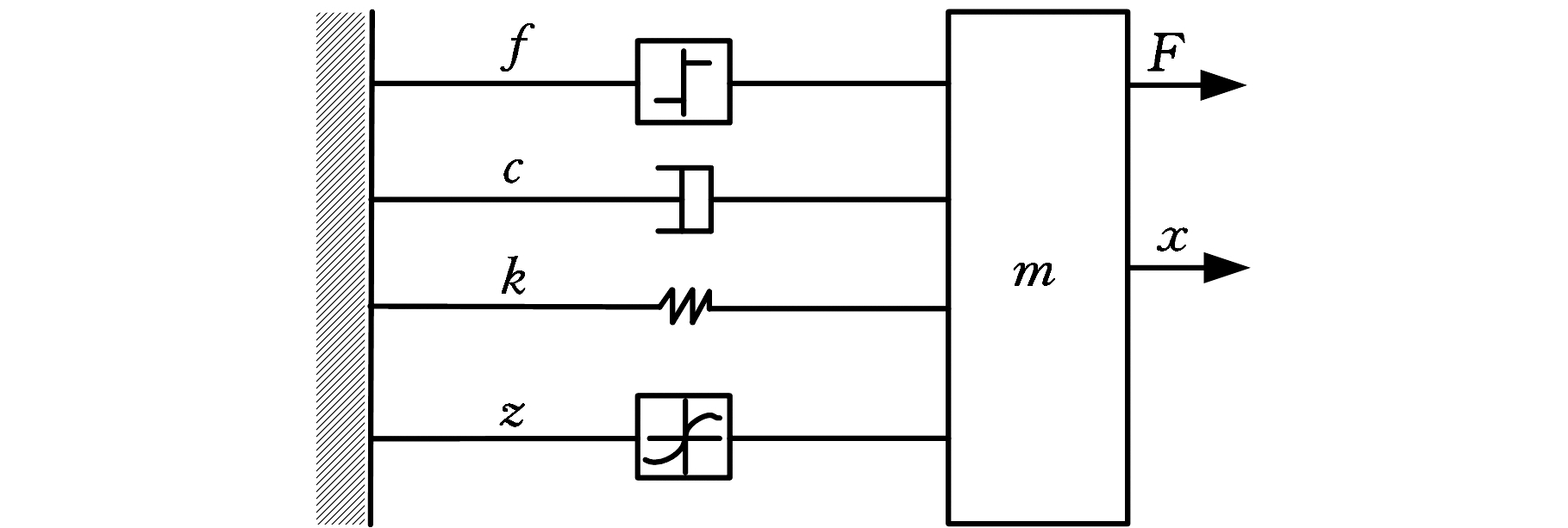
图1 魔术公式模型
Fig.1 Magic formula model
薛兵等[14]通过对磁流变减振器的运动学和流变学分析,将减振器的作用力分为剪切项、黏性项、摩擦项、弹性项和惯性项,如图1所示。磁流变减振器模型表达式为
(1)
式中,F为减振器输出阻尼力,N;f为摩擦力,N;k为刚度系数;c为黏性系数;n为惯性系数;Fb为剪切项,![]() 分别为减振器相对运动位移、速度、加速度,单位分别为mm、mm/s、mm/s2;x0为减振器活塞初始位移,mm。
分别为减振器相对运动位移、速度、加速度,单位分别为mm、mm/s、mm/s2;x0为减振器活塞初始位移,mm。
对于其中表征磁流变液特性的剪切项,使用魔术公式进行描述:
(2)
式中,D、C、B、E分别为峰值因子、形状因子、刚度因子和曲率因子。
变化魔术公式中的系数可以适应不同使用工况。该模型形式简单、参数一致且参数物理意义明确,磁流变魔术公式模型中与电流有关的参数较少,大大简化了辨识过程,更适合半主动悬架控制器的开发。
2 减振器特性实验
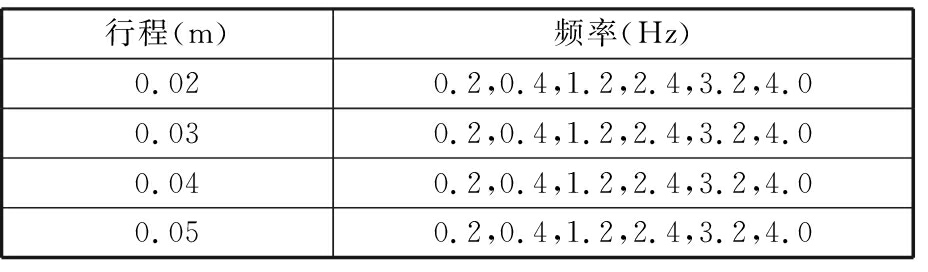
实验采用图2所示减振器动态特性测量系统和某款车型原装磁流变减振器。实验时,控制电流选择0、0.4A、0.8A、1.2A、1.6A和2.0A六种情况,激振行程及频率的选择见表1。

图2 减振器特性实验台
Fig.2 Damper characteristics test bench
表1 磁流变减振器特性实验方案
Tab.1 Magnet rheological damper characteristic test scheme
行程(m)频率(Hz)0.020.2,0.4,1.2,2.4,3.2,4.00.030.2,0.4,1.2,2.4,3.2,4.00.040.2,0.4,1.2,2.4,3.2,4.00.050.2,0.4,1.2,2.4,3.2,4.0
3 参数辨识
使用实验所得减振器特性数据进行参数辨识,其中2.4 Hz激振频率下得到的实验数据用于验证模型的准确性,不参与参数辨识。使用MATLAB优化工具箱,采用无约束非线性优化算法进行参数辨识,与电流、行程等无关的参数辨识结果如下:

(3)
魔术公式表示的剪切项中,各参数随控制电流的变化而变化,若各参数均考虑控制电流的影响,会使模型更加复杂,同时逆模型难以得到解析解,故需对模型适当简化。分析辨识结果可知,参数B、C和E随电流变化的程度并不大,如图3~图5所示,可简化为不依赖电流的定值,取B=0.003 767,C= 1.775,E= 1.295 2。
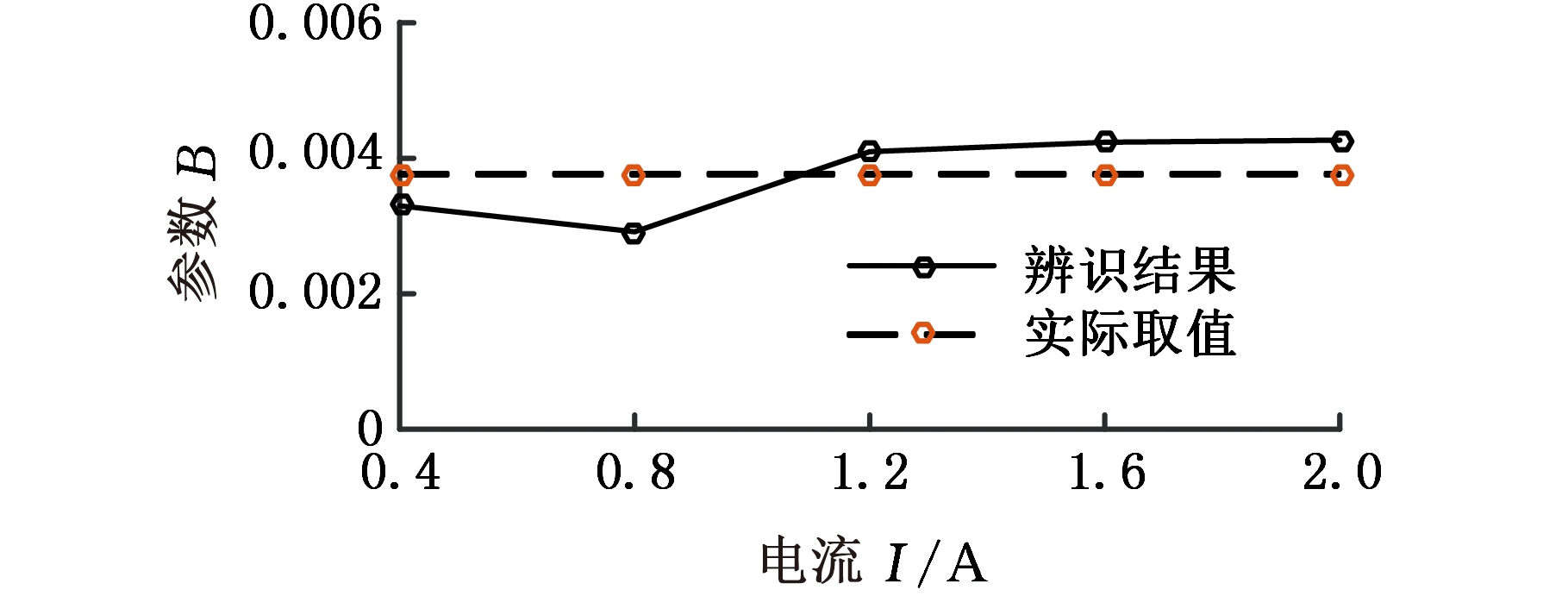
图3 参数B辨识结果
Fig.3 Parameter B identification results
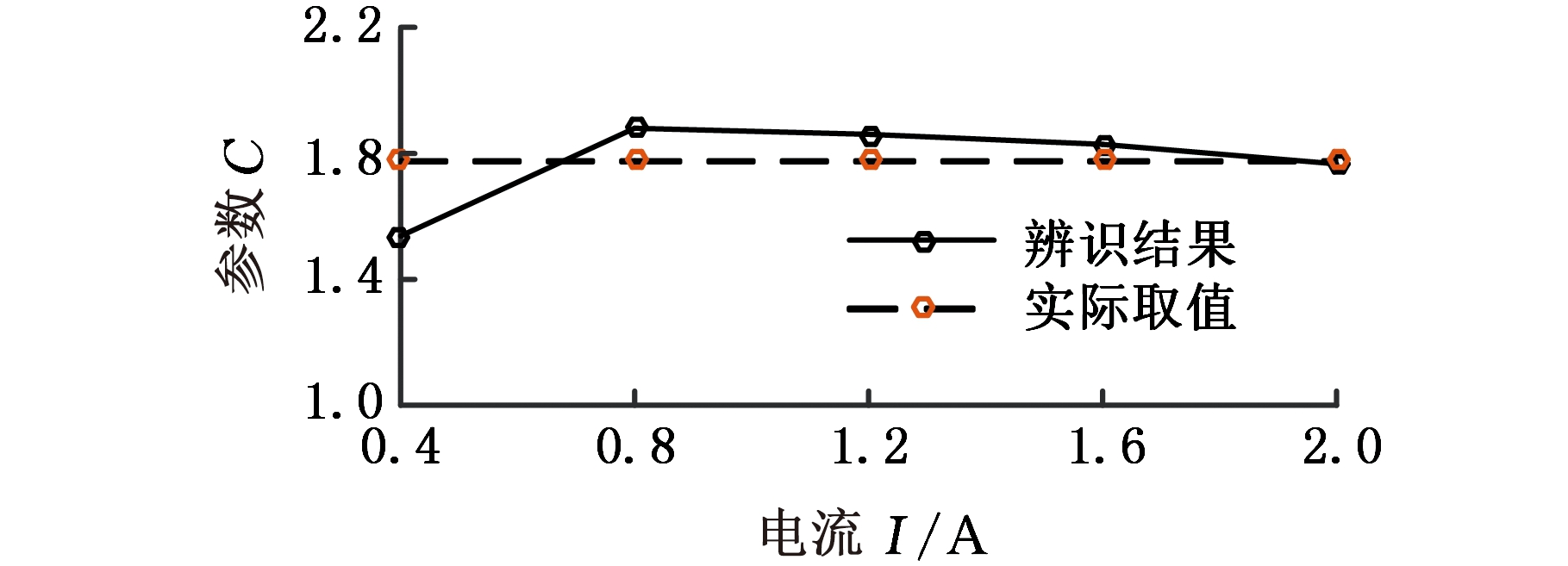
图4 参数C辨识结果
Fig.4 Parameter C identification results
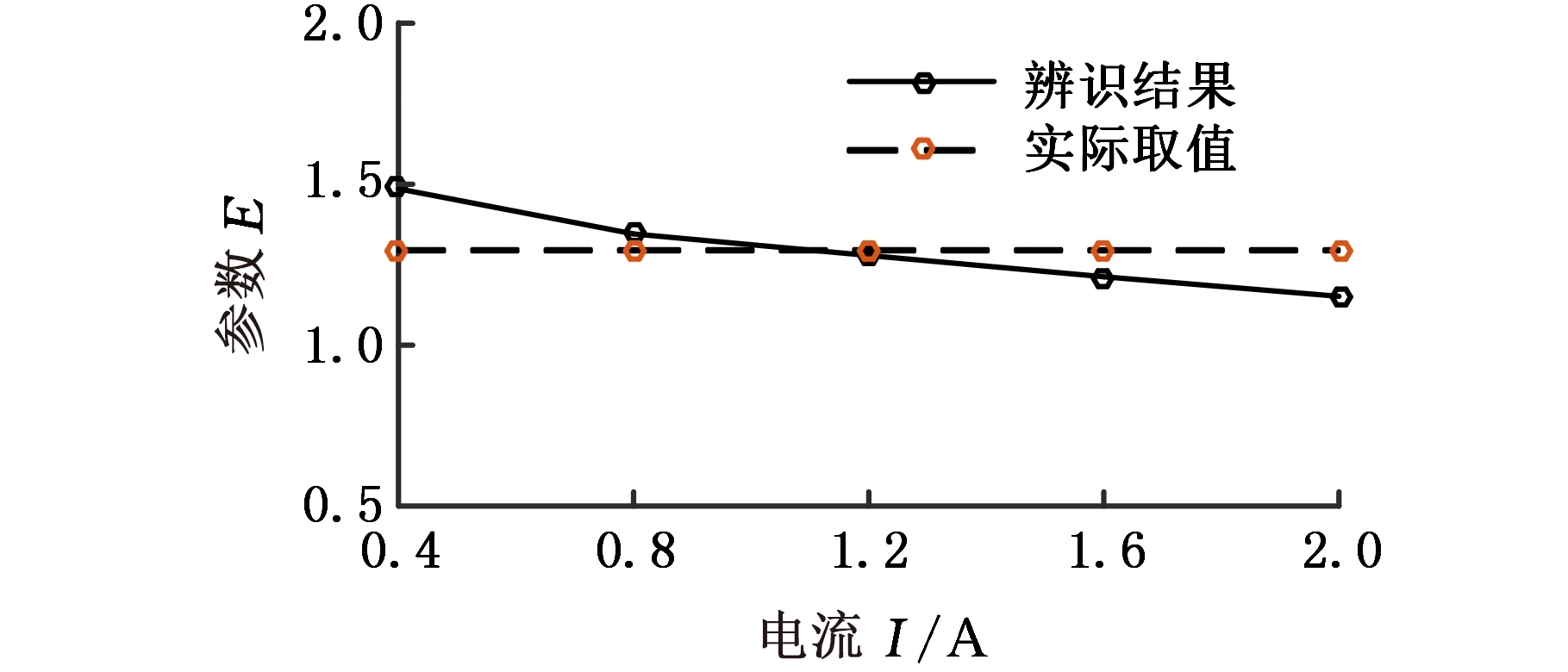
图5 参数E辨识结果
Fig.5 Parameter E identification results
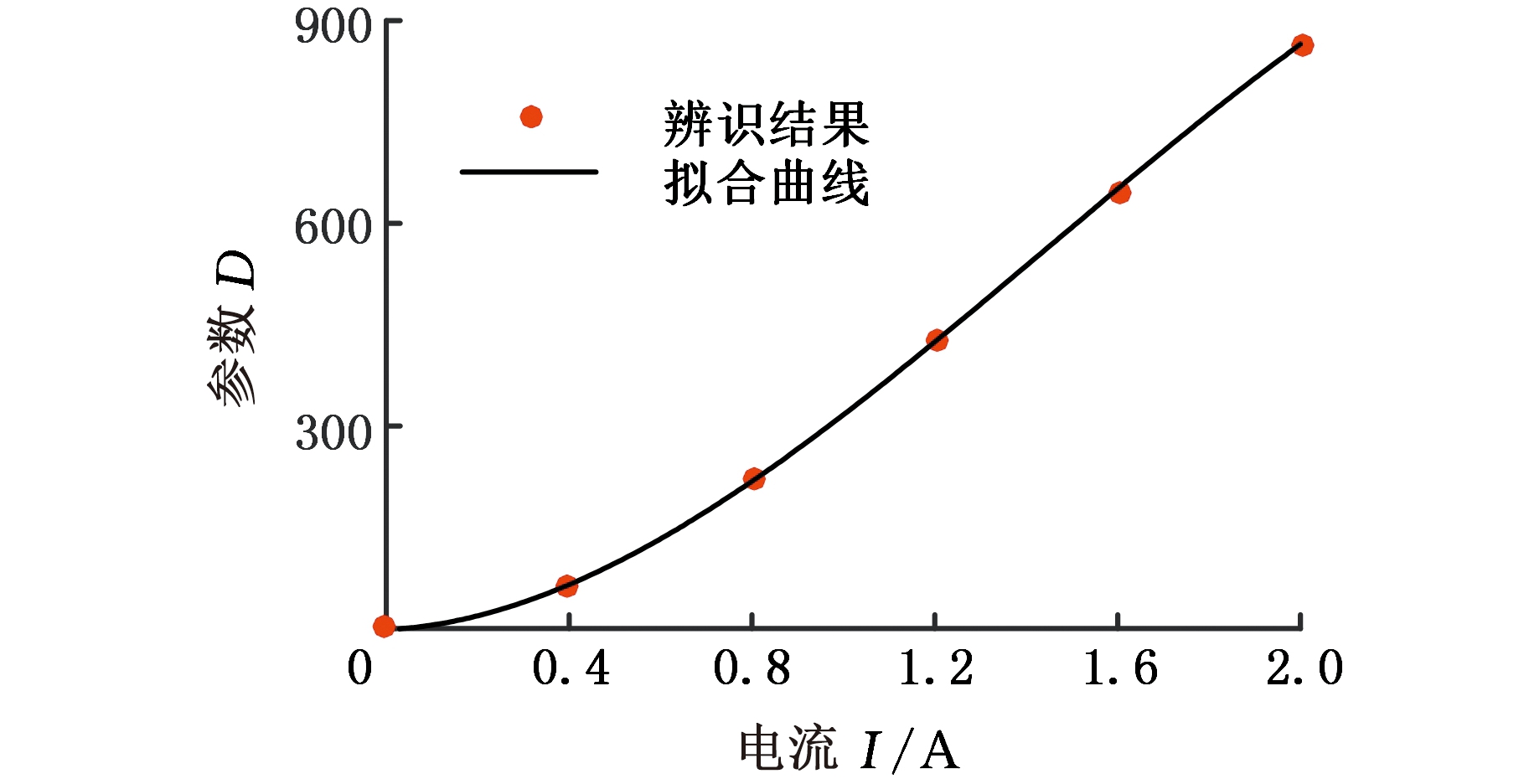
图6 参数D辨识结果
Fig.6 Parameter D identification results
由图6可知,参数D随电流的变化程度较大,需建立参数D和控制电流I的关系。对辨识结果进行数据拟合,得到参数D和控制电流I的关系:
D=-85.61I3+371.9I2+31.98I
(4)
根据已获得的各参数辨识结果和实验数据,进一步可辨识得到弹性项刚度系数k=2.732 N/mm,惯性项系数n=1.753 N/(m·s-2)。
使用2.4 Hz激振频率得到的实验数据验证磁流变减振器魔术公式模型的有效性,磁流变减振器实验所得速度特性和模型所得速度特性对比如图7所示。2.4 Hz激振各电流下模型拟合实验数据的误差如图8所示。由图8可知,模型误差基本保持在8%以内。使用误差e定量表示模型的精度,有
(5)
式中,Fm为模型输出的阻尼力;Ft为实验得到的阻尼力。

图7 2.4 Hz激振各电流下模型拟合实验数据速度特性
Fig.7 Velocity characteristics of model fitting test data
under 2.4 Hz excitation current
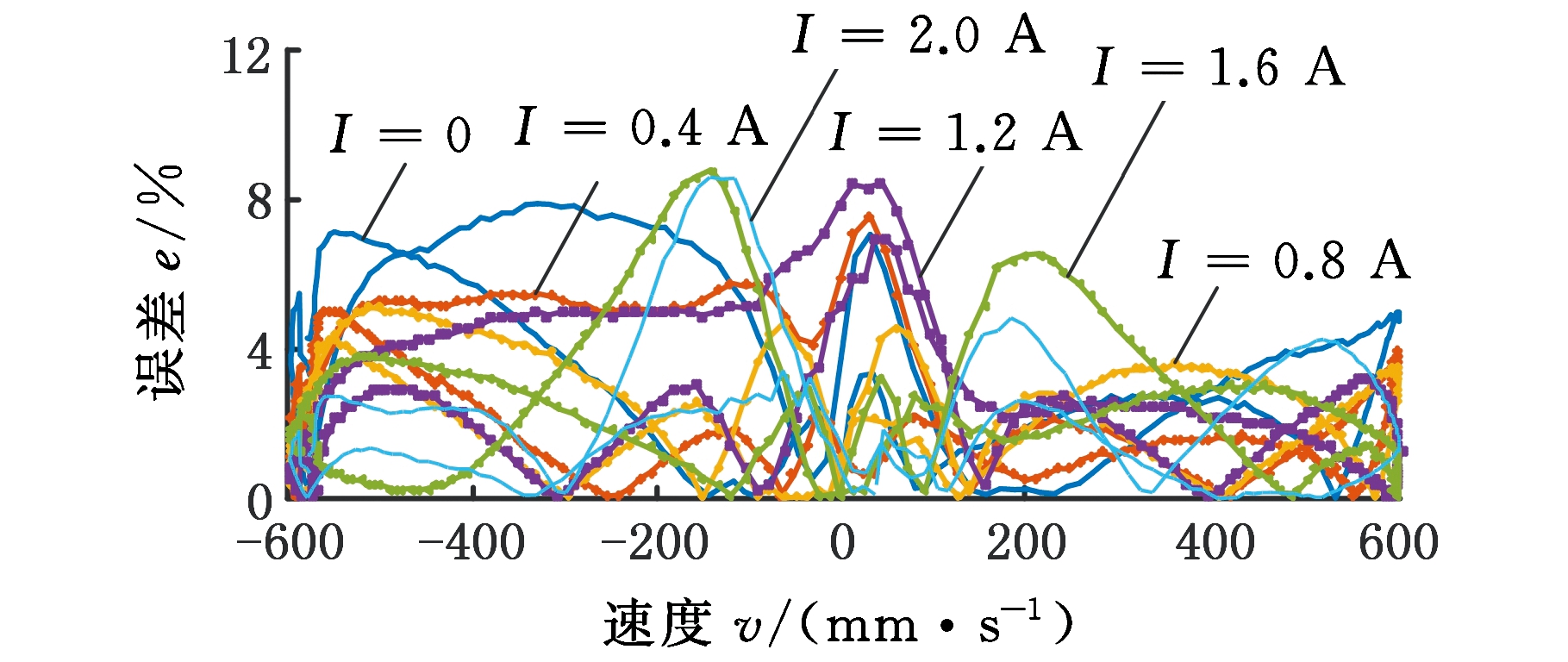
图8 2.4 Hz激振各电流下模型拟合实验数据误差
Fig.8 Error of model fitting test data under 2.4 Hz
excitation current
4 逆模型的建立
悬架控制器根据控制算法计算出的期望阻尼力给被控减振器一个准确电流指令。磁流变减振器逆模型即表示期望阻尼力和激励电流之间的非线性关系。因在磁流变减振器魔术公式模型辨识的过程中做了适当简化,其中仅参数D与电流有关,故可以直接逆推得到逆模型。
本文不求解I和D的解析关系,根据式(4)建立一个分段函数I=H(D),如图9所示,限定控制电流I∈[0,2]A。用分段函数的形式表示I-D关系,相当于在控制过程中采用局部查表的方法,可以提高程序运行的速度;分段函数中控制电流的分辨率为0.1 A,在降低控制电流变化频率的同时并不会对期望输出阻尼力产生显著的影响。磁流变减振器魔术公式逆模型如下:
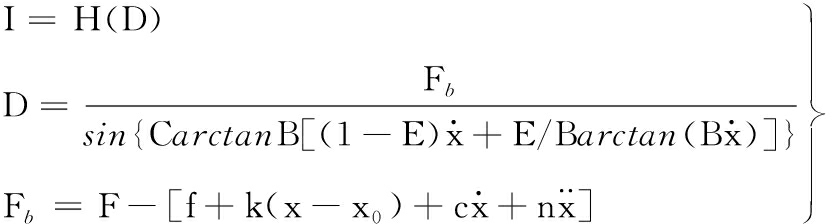
(6)

图9 参数D与控制电流关系
Fig.9 Relationship between parameter D and
control current
5 仿真研究
根据上文得到的磁流变减振器魔术公式正向及逆向动力学模型,在MATLAB/Simulink中建立二自由度1/4车辆磁流变半主动悬架系统仿真模型,如图10所示,悬架系统主要参数见表2。
表2 悬架系统参数
Tab.2 Suspension system parameters

簧上质量(kg)500簧下质量(kg)50弹簧刚度(N/mm)42.1轮胎刚度(N/mm)491.58
使用加速度驱动阻尼控制(acceleration driven damper control,ADD)策略,其数学表达式如下:
(7)
式中,cs为控制策略计算阻尼系数; cmax、cmin分别为最大、最小阻尼系数;![]() 为簧上质量垂向运动速度;
为簧上质量垂向运动速度;![]() 为簧下质量运动速度。
为簧下质量运动速度。
由图10可知,ADD控制策略根据车身加速度和悬架系统相对速度信号得到期望阻尼力。磁流变减振器魔术公式逆模型根据期望阻尼力、悬架系统相对速度及动挠度信号计算出实现期望阻尼力所需的控制电流。磁流变减振器魔术公式正模型根据控制电流、相对速度及动挠度信号计算出模拟实际磁流变减振器输出阻尼力并输入悬架系统模型中,从而实现完整的磁流变半主动悬架系统仿真模型。
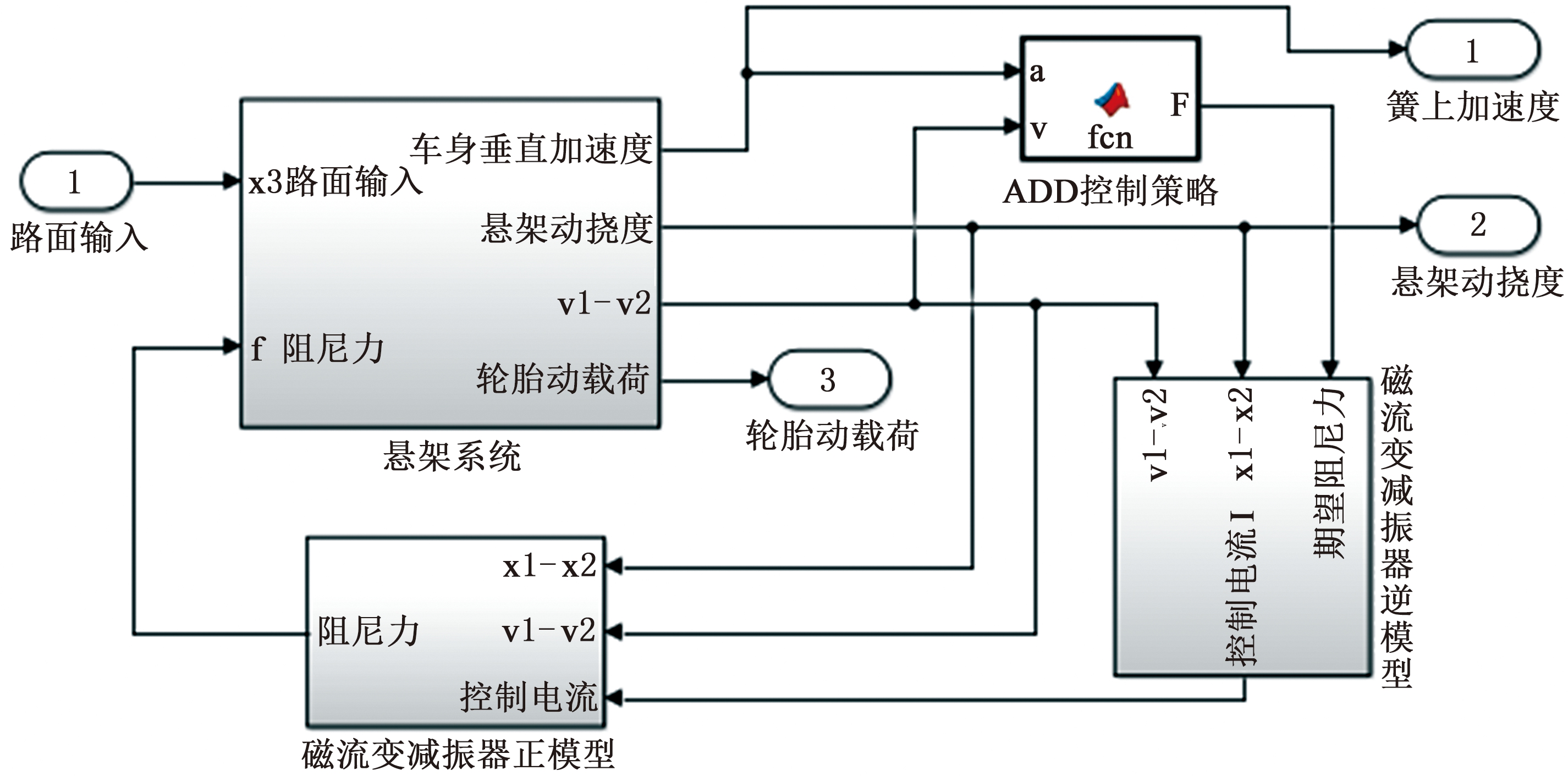
图10 磁流变半主动悬架系统仿真模型
Fig.10 Simulation model of magnetorheological semi-active suspension system
选择B级路面进行随机路面激励仿真,设定车速为36 km/h。磁流变减振器魔术公式逆模型输出控制电流如图11所示,磁流变减振器魔术公式正模型输出模拟实际输出阻尼力和由ADD控制策略给出的期望阻尼力对比如图12所示。对模拟实际阻尼力和期望阻尼力进行误差分析,如图13所示,可知减振器模型实现期望阻尼力的最大误差为16%左右,误差平均值为3.67%。
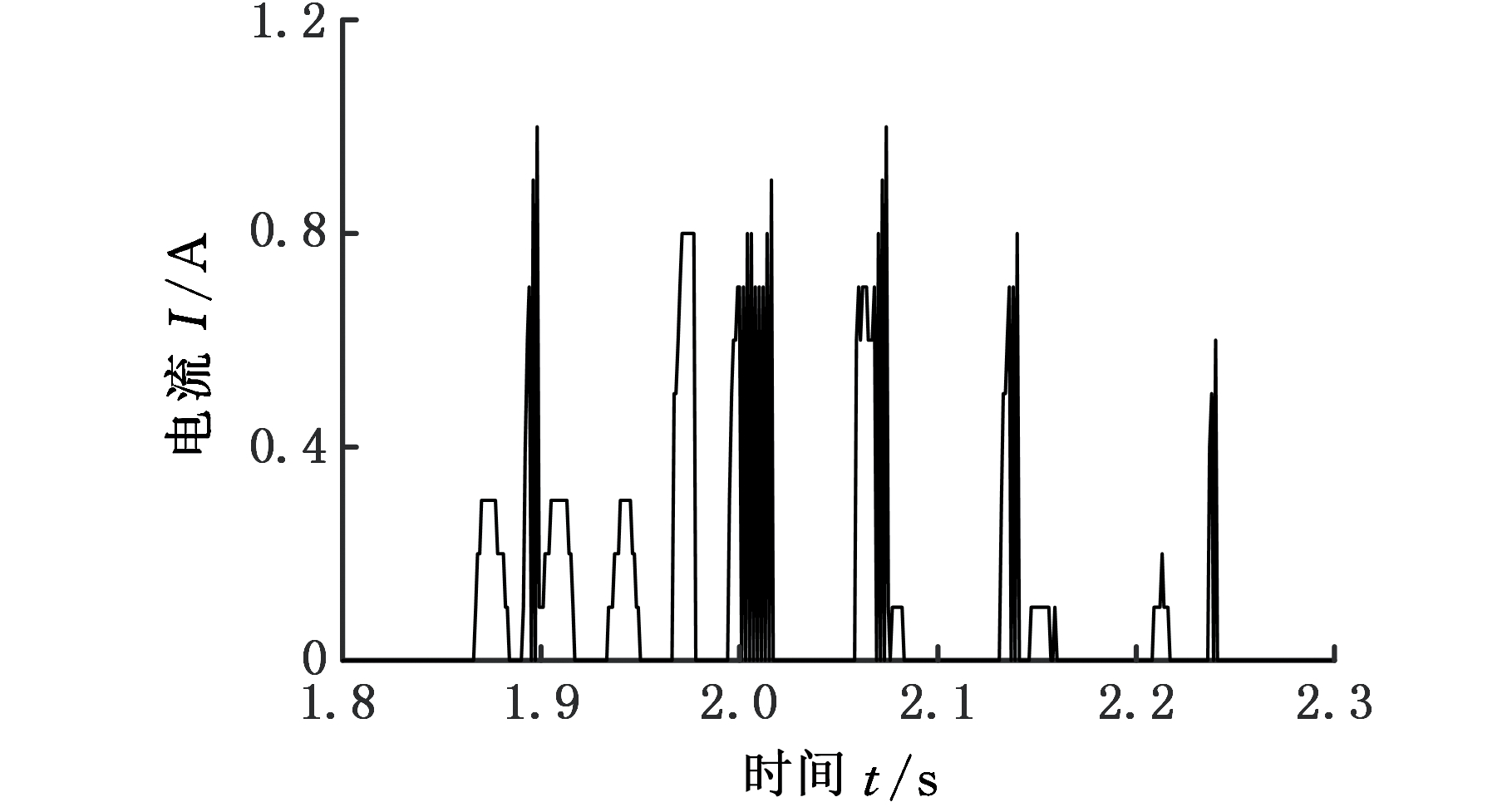
图11 控制电流
Fig.11 Control current
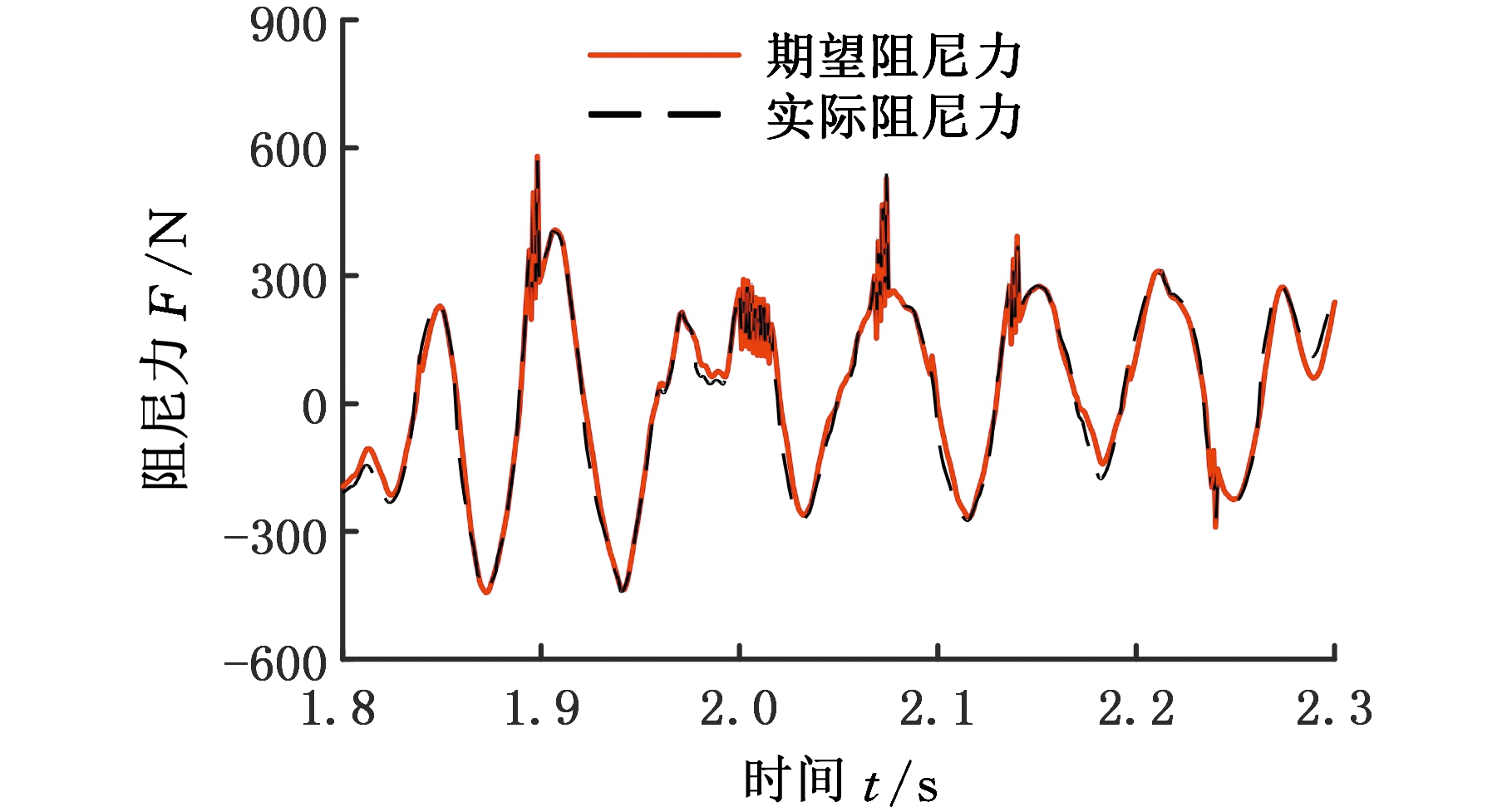
图12 期望及模拟实际阻尼力对比
Fig.12 Comparison of expected and simulated
actual damping forces
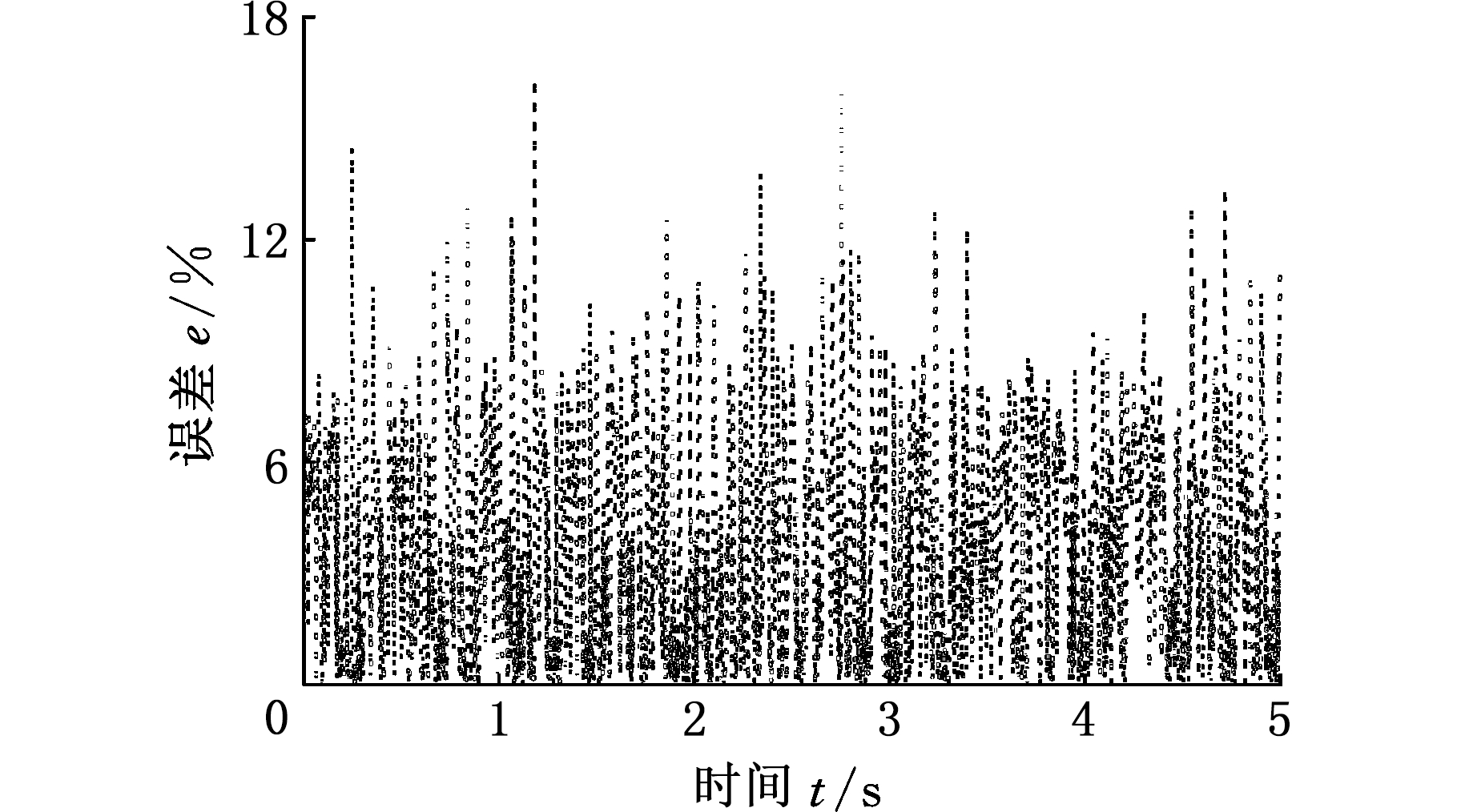
图13 减振器模型实现期望阻尼力的误差
Fig.13 Error of the damper model to achieve the
desired damping force
悬架系统对车辆乘坐舒适性、操纵稳定性和安全性有重要影响,常以车身加速度、悬架动挠度和轮胎动载荷作为评价悬架系统性能的指标。根据实验得到的磁流变减振器阻尼力可调范围,选择一个适中的恒定阻尼系数c0=2 000 N/(m·s-1)建立二自由度1/4车辆被动悬架系统仿真模型。使用相同的随机路面激励工况,对比磁流变半主动悬架和被动悬架系统性能表现,如图14~图16及表3所示。由表3可知,ADD控制下的磁流变半主动悬架系统对车身加速度代表的车辆的乘坐舒适性有较明显的改善,而对操纵稳定性和安全性不利。
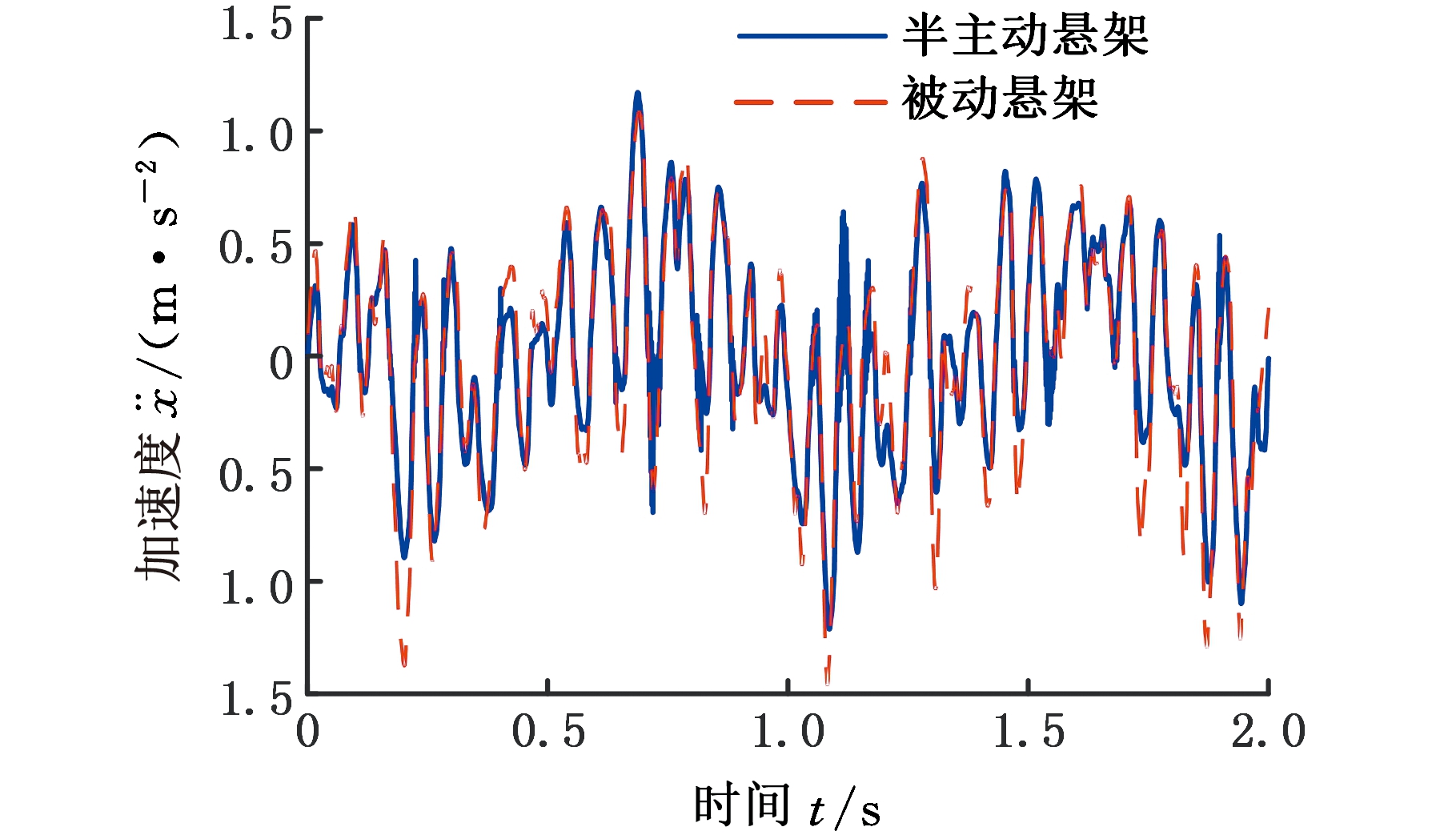
图14 半主动与被动悬架车身加速度仿真结果
Fig.14 Semi-active and passive suspension body
acceleration simulation results
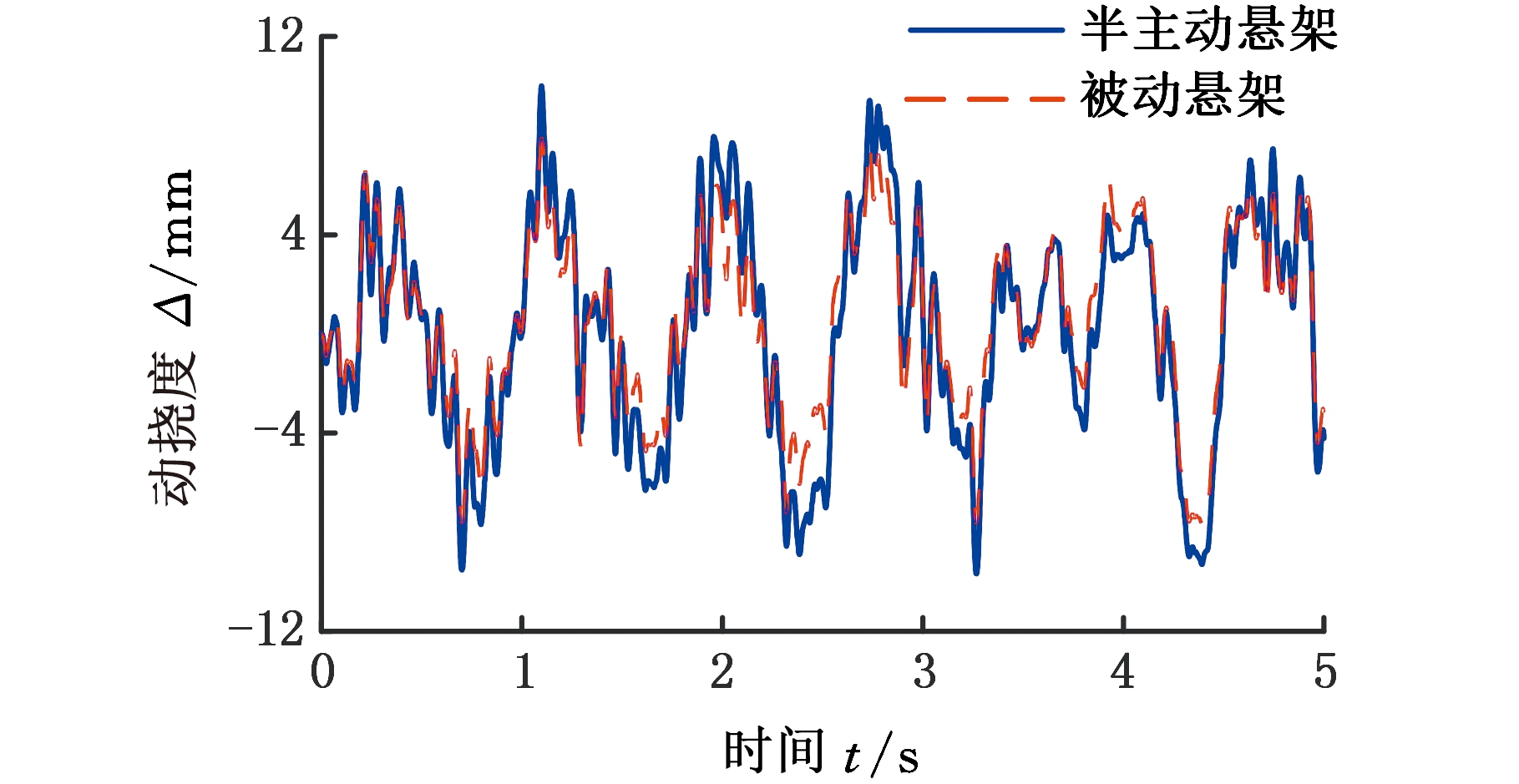
图15 半主动与被动悬架动挠度仿真结果
Fig.15 Simulation results of dynamic deflection of
semi-active and passive suspension

图16 半主动与被动悬架轮胎动载荷仿真结果
Fig.16 Simulation results of tire dynamic loads of
semi-active and passive suspension
表3 随机路面激励各评价指标均方根值
Tab.3 RMS value of each evaluation index of random road excitation
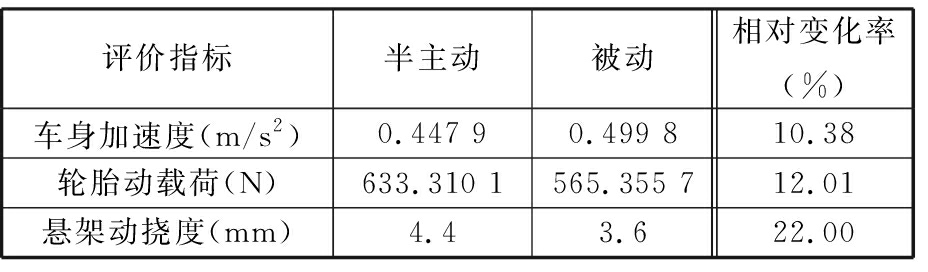
评价指标半主动被动相对变化率(%)车身加速度(m/s2)0.447 90.499 810.38轮胎动载荷(N)633.310 1565.355 712.01悬架动挠度(mm)4.43.622.00
6 台架实验
6.1 实验设备
通过磁流变半主动悬架系统台架实验,将磁流变减振器魔术公式模型应用于实际磁流变半主动控制中。台架实验在磁流变半主动悬架控制算法验证平台上进行,如图17所示,它主要由1/4车辆悬架系统模型、磁流变减振器、传感器、激振系统、Test.Lab实验测试系统和快速原型控制器等组成。
6.2 半主动控制程序
快速原型控制器拥有基于Simulink的驱动程序库,可在Simulink环境中建立完整的控制程序。在Simulink中建立的包含底层输入、输出驱动程序、ADD控制策略和磁流变减振器魔术公式逆模型的磁流变半主动悬架控制程序如图18所示。簧上质量加速度传感器及车身高度传感器信号分别通过“AD”采集模块进入主控制程序;ADD控制策略根据簧上质量加速度信号和悬架系统相对运动速度信号计算出期望阻尼力;磁流变减振器逆模型根据期望阻尼力和悬架系统相对运动速度及位移信号计算得出磁流变减振器实现期望阻尼力所需的控制电流;控制电流通过“PWM Output”输出驱动程序模块输入磁流变减振器,从而改变减振器阻尼系数,实现半主动控制。

图17 磁流变半主动悬架控制算法验证平台
Fig.17 Magnetorheological semi-active suspension
control algorithm verification platform
将建立的控制程序编译载入控制器中,即可开始悬架系统半主动控制激振实验。
6.3 实验工况
选择B级随机路面激励,分别对安装有被动阻尼器(图19)和磁流变减振器(图20)的被动悬架和半主动悬架进行激振实验。其中,磁流变阻尼器可实现的最小阻尼系数约为被动阻尼器的0.5倍,最大阻尼系数约为被动阻尼器的2倍。
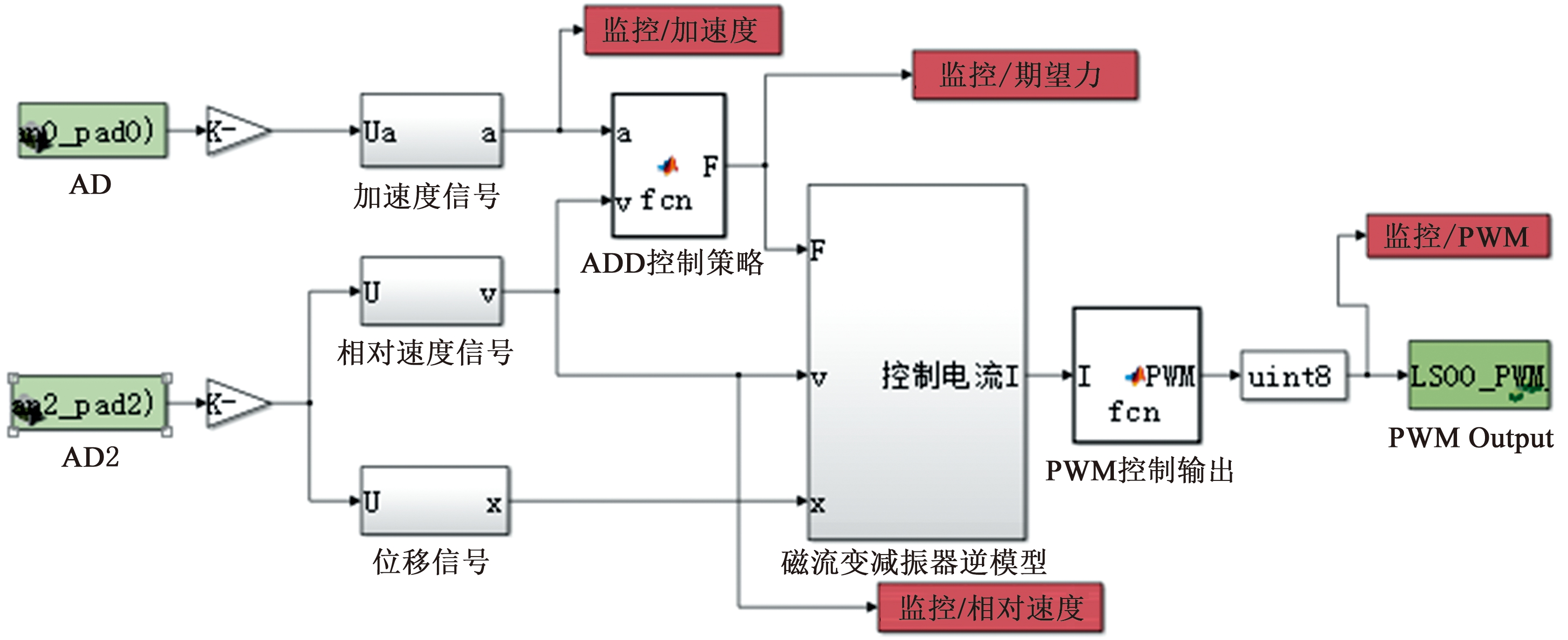
图18 磁流变半主动悬架控制程序
Fig.18 Magnetorheological semi-active suspension control program

图19 被动减振器 图20 磁流变减振器
Fig.19 Passive damper Fig.20 Magnetorheologicaldamper
6.4 实验结果分析
鉴于实验设备的局限性,无法获得车轮动载荷或轮胎变形的信号,故只给出车身加速度和悬架动挠度的实验结果,如图21、图22所示。
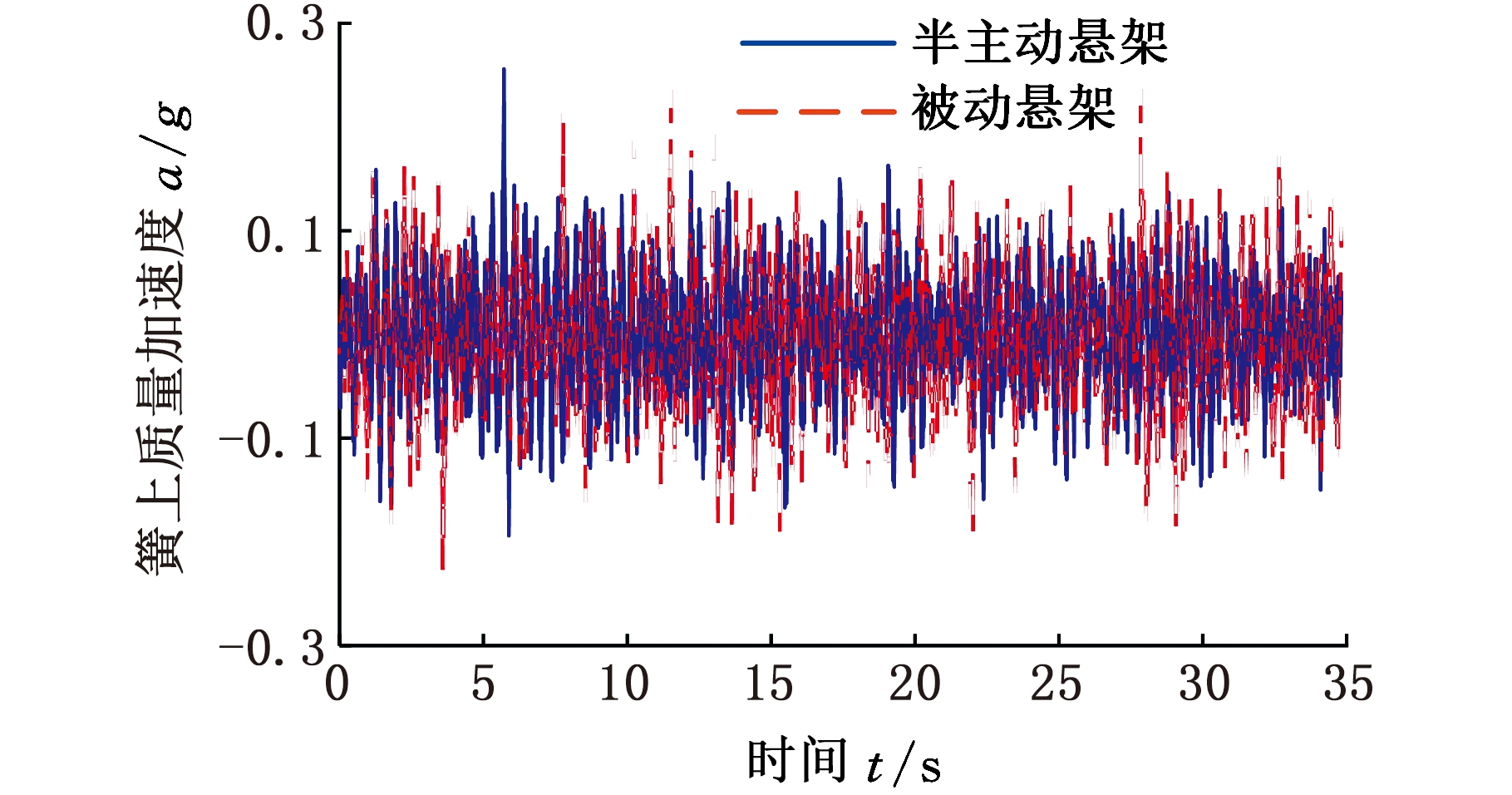
图21 车身加速度实验结果
Fig.21 Body acceleration test results
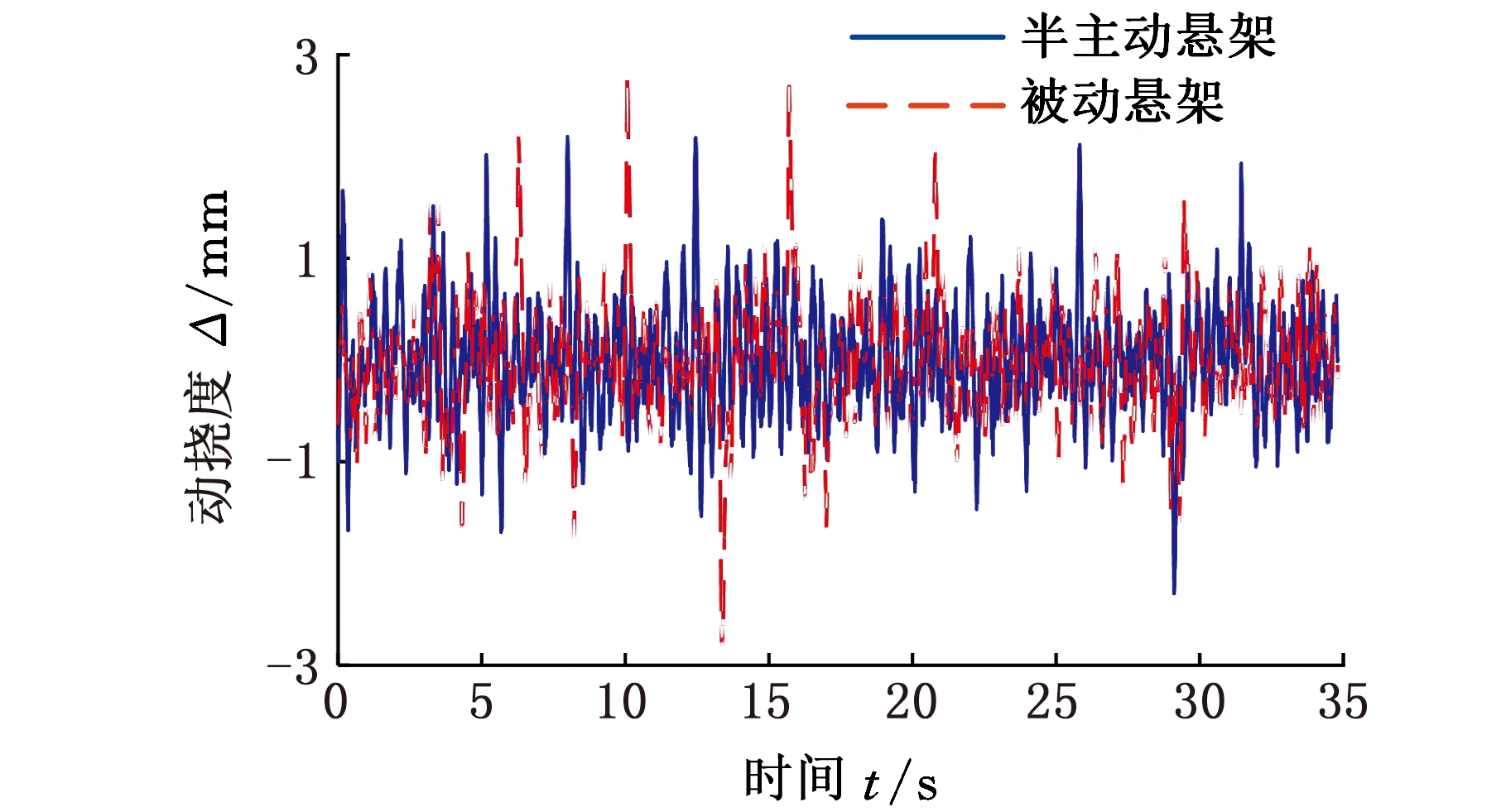
图22 悬架动挠度实验结果
Fig.22 Suspension dynamic deflection test results
随机路面激励各评价指标均方根值见表4。由表4可知,使用ADD控制策略和磁流变减振器魔术公式逆模型控制的磁流变半主动悬架相对于被动悬架,车身加速度降低了6.27%,悬架动挠度增加了2.6%。和仿真结果相比,虽然性能变化程度不同,但车辆乘坐舒适性的提高对操纵稳定性和安全性不利的结论是一致的。这说明磁流变减振器逆模型在半主动悬架台架实验的应用过程中实现了ADD控制的效果。
表4 随机路面激励各评价指标均方根值
Tab.4 RMS value of each evaluation index of random road excitation
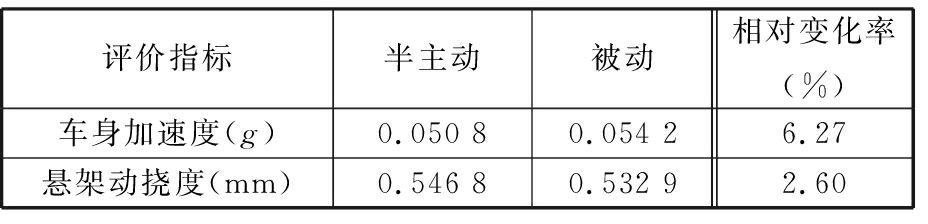
评价指标半主动被动相对变化率(%)车身加速度(g)0.050 80.054 26.27悬架动挠度(mm)0.546 80.532 92.60
7 结论
(1)仿真过程中,磁流变减振器魔术公式正逆模型实现ADD控制策略给出的期望阻尼力的最大误差为16%,误差平均值为3.67%,该模型较好地实现了期望阻尼力,提高了车辆乘坐舒适性。
(2)台架实验中,ADD控制策略给出期望阻尼力,通过磁流变减振器魔术公式逆模型得出控制电流,以实现对减振器的控制,相对于被动悬架,车身加速度降低了6.27%,悬架动挠度增大了2.6%。
(3)在仿真和台架实验中,磁流变减振器魔术公式模型的应用均实现了ADD控制策略,有利于提升车辆悬架系统舒适性的效果。
本文通过对磁流变减振器魔术公式模型的应用研究,为磁流变半主动悬架实现理想的控制效果做出了有益的探索。
[1] WEBER F. Bouc-Wen Model-based Real-time Force Tracking Scheme for MR Dampers [J]. Smart Materials and Structures, 2013, 22(4): 045012.
[2] MIAH M S, CHATZI E N, DERTIMANIS V K, et al. Nonlinear Modeling of a Rotational MR Damper via an Enhanced Bouc-Wen Model [J]. Smart Materials and Structures, 2015, 24(10): 105020.
[3] CHEN P, BAI X X, QIAN L J, et al. An Approach for Hysteresis Modeling Based on Shape Function and Memory Mechanism [J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(3): 1270-1278.
[4] BOUC R. A Mathematical Model for Hysteresis [J]. Acta Acustica United with Acustica, 1971, 24(1): 16-25.
[5] WEN Y K. Method for Random Vibration of Hysteretic System [J]. Journal of the Engineering Mechanics Division, 1976, 102(2): 249-263.
[6] SPENCER B F, DYKE S J, SAIN M K, et al. Phenomenological Model for Magnetorheological Dampers [J]. Journal of Engineering Mechanics, 1997, 123(3): 230-238.
[7] CANUDAS-DE-WIT C, OLSSON H, ASTROM K J, et al. A New Model for Control of Systems with Friction [J]. IEEE Transactions on Automatic Control, 1995, 40(3): 419-425.
[8] LISCHINSKY P, CANUDAS-DE-WIT C, MOREL G. Friction Compensation for an Industrial Hydraulic Robot [J]. IEEE Control Systems, 1999, 19(1): 25-32.
[9] JIMNEZ R, ALVAREZ L. Real Time Identification of Structures with Magnetorheological Dampers[C]∥ Proceedings of the 41st IEEE Conference on Decision and Control. Las Vegas, 2002: 1017-1022.
[10] JIMNEZ R, ALVAREZ L. LuGre Friction Model for a Magnetorheological Damper [J]. Structural Control & Health Monitoring, 2010, 12(1): 91-116.
[11] SAKAI C, OHMORI H, SANO A. Modeling of MR Damper with Hysteresis for Adaptive Vibration Control[C]∥ 42nd IEEE International Conference on Decision and Control. Maui, 2004: 3840-3845.
[12] TSANG H H, SU R K L, CHANDLER A M. Simplified Inverse Dynamics Models for MR Fluid Dampers [J]. Engineering Structures, 2006, 28(3): 327-341.
[13] BAHAR A, POZO F, ACHO L, et al. Hierarchical Semi-active Control of Base-isolated Structures Using a New Inverse Model of Magnetorheological Dampers [J]. Computers & Structures, 2010, 88(7/8): 483-496.
[14] 薛兵, 杜永昌, 刘源,等. 基于机理的磁流变减震器滞回特性魔术公式模型[J].振动工程学报, 2017, 30(5):774-780.
XUE Bing, DU Yongchang, LIU Yuan, et al. A Mechanism-based Magic Formula Model for Hysteretic Characteristics of Magneto Rheological Damper [J]. Journal of Vibration Engineering, 2017, 30(5): 774-780.
