0 引言
在钢铁行业中,国内节能降耗的相关研究大都集中在炼铁、炼钢、铸钢等前几道工序,在这些工序上,我国与国外钢铁行业先进的国家差距不是特别大。但是,我国钢铁企业在冷轧生产中把关注点放在交货期和产品质量上,忽视了冷轧能量的消耗,导致钢铁行业总体能量利用率不高,基本不超过67%,而冷轧工序的节能降耗相关研究也很少。我国轧制工序的能量利用效率与国际先进水平相比差距巨大(近50%)[1-2]。
目前,中外学者对连续退火产线(以下简称“连退产线”)生产工艺参数及排序优化的研究尚处于起步阶段,相关文献较少,主要集中在机床领域,主要是单目标或多目标的工艺参数优化以及基于能效的工艺参数优化等。
单目标参数优化研究已较为成熟,该方向的研究大多采用智能优化算法。GAO等[3]通过粒子群算法对机床中的相关参数实施优化分析。
多目标工艺参数优化更为复杂,是目前许多学者较为青睐的研究方向,其中采用的智能优化算法比较多,如PARK等[4]采用的BP算法、马峰等[5]采用优化模型进行求解的方法。
钢铁行业工艺系统参数优化的研究较少。 POURSINA等[6]基于遗传算法,利用一个多目标函数对冷轧损伤和能耗进行优化,首次实现了用损伤力学优化建模,并提出了轧制时间表的概念。
关于调度优化,现有研究主要集中于热轧生产中的调度排序。唐立新等[7-8]开发了一种新型的改进遗传算法,并将其与人机交互理念结合,开发了调度系统,通过改进局域搜索算法解决了热轧厂中钢坯的存放问题。
关于连退计划排序优化的研究报道较少。WANG 等[9]采用了动态约束蚁群算法完成排序的求解。VERDEJO等[10]通过局域搜索算法解决了镀锌机组中的生产排序问题。
本文以连退机组为对象进行分析,建立了能量消耗与工艺参数之间的能耗模型,结合智能优化算法获取不同钢种的最佳生产工艺参数;同时以能量效率、产品质量、交货期等为优化指标,建立多约束的多目标生产作业计划单产线排序优化模型,结合现有可靠性高的多目标智能优化算法对该产线的生产排序进行优化求解,以获取最佳生产排序方式。
1 建模分析
1.1 能量流分析
将退火炉的预热、加热以及均热段视为一个整体,分析其能量流组成。图1所示为连续退火炉加热区传热过程。在炉区中,主要是以热能形式在机组中流动,电能消耗非常小,基本可以忽略不计,其热输入为煤气燃烧的燃料化学热Qr,热输出为带钢带走热量Qg、废气带走热量Qf、炉壁表面散失热量Qb、保护气体带走热量Qbh以及预热空气所需的热量Qk,其能量示意图见图2。因此最终能量流模型的构成如下:
Qr=Qg+Qf+Qb+Qbh+Qk
(1)

图1 炉区加热区传热过程
Fig.1 Heat transfer process in heating zone
of furnace zone
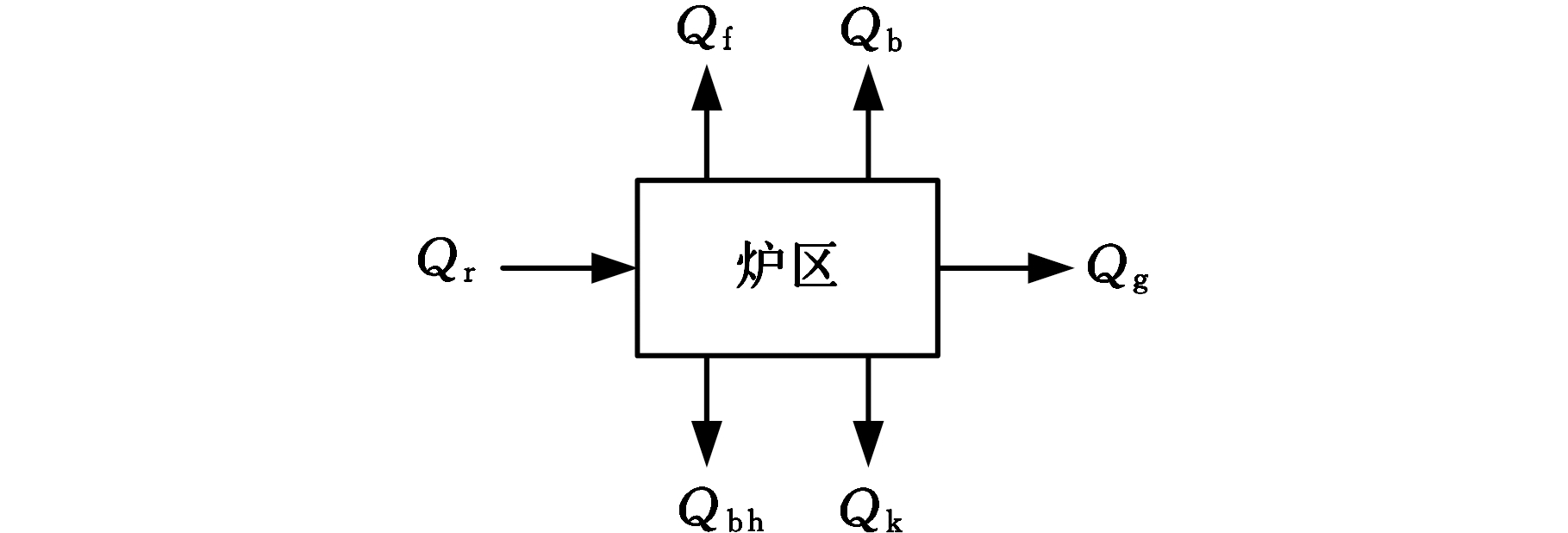
图2 炉区能量流向示意图
Fig.2 Schematic diagram of energy flow in
furnace zone
1.2 能量流模型
1.2.1 热输入
退火炉中,能量的输入主要为热量,而热量主要来自煤气的燃烧产生的化学热,其求解公式为
Qr=qz Qd
(2)
式中,Qr单位为kJ/min;qz为煤气总通气量,m3/min;Qd为燃烧气体热值,kJ/m3(自然状态)。
1.2.2 热输出
(1)带钢带走热量。带钢加热时吸收热量,通常计算带钢的温升时把带钢密度ρ和定压热容CG视为常量。然而连退工艺中温度变化大,对应的定压比热容有很大变化,因此本文引入带钢定压比热容-温度模型,当带钢温度的绝对温度T在100~1 500 K范围内时,带钢定压热容(MJ/(t·K))计算公式如下:
CG(T)=1.34×10-11T5-3.7×10-8T4+
4.007×10-5T3-0.021 01T2+5.672T-179.6
(3)
带钢带走热量由带钢单位时间产量、退火温度、环境温度以及对应定压比热容决定,具体计算如下:
Qg=WCG(T1-T0)=vldρ![]() G(T)dT
G(T)dT
(4)
式中 ,Qg单位为kJ/min;W 为机组标准生产率,t/min;CG单位为kJ/(t·K);T1为带钢出加热炉的温度,K;T0为环境温度,K;v为带速,m/min;l为带宽,m;d为带厚,m;ρ为密度,kg/m3;T为随加热而变化的温度,K。
(2)废气带走热量。在连退产线,废气带走热量是能量损耗的主要原因,因此,废气能耗的计算对模型的建立十分重要。废气带走热量计算公式如下:
Qf=Vf Cf(T3-T0)=L0Va Cf(T3-T0)
(5)
(6)
(7)
式中,Qf单位为kJ/min;Vf为废气总量(标态),m3/min;Cf为废气热容(标态),kJ/(m3·K);T3为最终废气温度,K;Va为单位燃烧生成气体量,m3/m3;L0为单位理论空气消耗量,m3/m3;α为空气过剩系数,取1.05~1.1。
(3)炉壁表面散失热量。炉体稳定散热主要流程为炉体内壁受到内部保护气体的对流加热以及钢带对炉体的辐射加热(其中主要受热形式为对流受热),然后墙体通过不锈钢板以及两层保温层的热传递后,在炉壁与外界环境通过对流换热形式散失热量。 在计算过程中,墙体温度可以通过下式求解:
(8)
式中,T4j为炉区温度,K,j取2、3分别对应加热段、均热段;T5为带钢出口温度,K;Ti为带钢出口温度和带钢入口温度的平均值,K;F为计算单元辐射系数;σ0为Stefan-Boltznmann常数。
最后可得炉壁表面散失热量求解公式[11]:
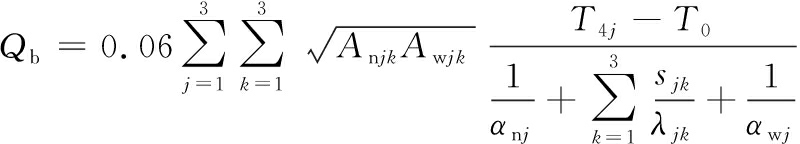
(9)
式中,S为热交换面积,m2;λ为材料热导率,W/(m2·K);αn为炉墙内表面传热系数,W/(m2·K);αw为炉墙外表面传热系数,W/(m2·K);An为炉墙内表面面积,m2;Aw为炉墙外表面面积,m2;j取1、2、3分别对应预热炉、加热炉、均热炉;k取1、2、3分别对应炉墙、炉顶、炉底。
(4)保护气体带走热量。退火产线为了避免炉内高温状态带钢被空气氧化,需要充入足量保护性气体来对带钢进行保护,在这个过程中,这部分气体会消耗部分能量导致能量损失,求解如下:
(10)
式中,Qbh单位为kJ/min;qbj为对应炉区保护气体通入量(标态),m3/min;Cbj为对应炉区保护气体热容,kJ/(m3·K); T5j为保护气体出退火炉的温度,K。
(5)预热空气所需的热量。为了充分利用能源,通常空气会被废气预热后再通入燃烧室,其预热所需的能量如下:
Qk=qzαL0Ck(Tk-T0)
(11)
式中,Qk单位为kJ/min; qz为煤气通入量;Ck为空气的热容,kJ/(m3·K);Tk为进入烧嘴时空气预热温度,K。
1.2.3 连续退火炉炉区热平衡模型
连续退火炉炉区的热平衡计算过程中,忽略了一部分能量占比较小的能耗或者仅前期加热炉区需要而后期不需要的能量,如金属氧化热、辅助工件与炉墙蓄热、逸出气体损失热以及化学不完全燃烧热损失(占比不足1%)。本研究主要针对能量消耗较大的区域,结合式(2)、式(4)、式(5)、式(9)、式(10)、式(11),连续退火炉炉区热平衡方程为[12]
Qr=qz Qd=vldρ![]() G(T)dT+Vf Cf(T3-T0)=
G(T)dT+Vf Cf(T3-T0)=![]()
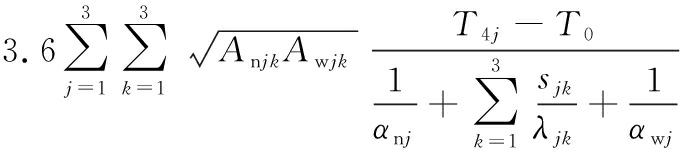
(12)
1.3 数学模型
将已知参数量代入式(12)中,可得
Qr=7 530qz=7 850vld![]() CG(T)dT+
CG(T)dT+
85.914 8[9.550 7×1010d![]() CG(T)dT+
CG(T)dT+![]()
![]()
![]()
1.1485×104+7 850vld![]() CG(T)dT}
CG(T)dT}
(13)
1.4 模型验证
由上文可知,能量消耗模型主要与带速v、退火温度T1及最终煤气通入量qz3个参数相关,为了验证本模型的准确性与可靠性,本研究中选取了两组不同的数据进行解析。
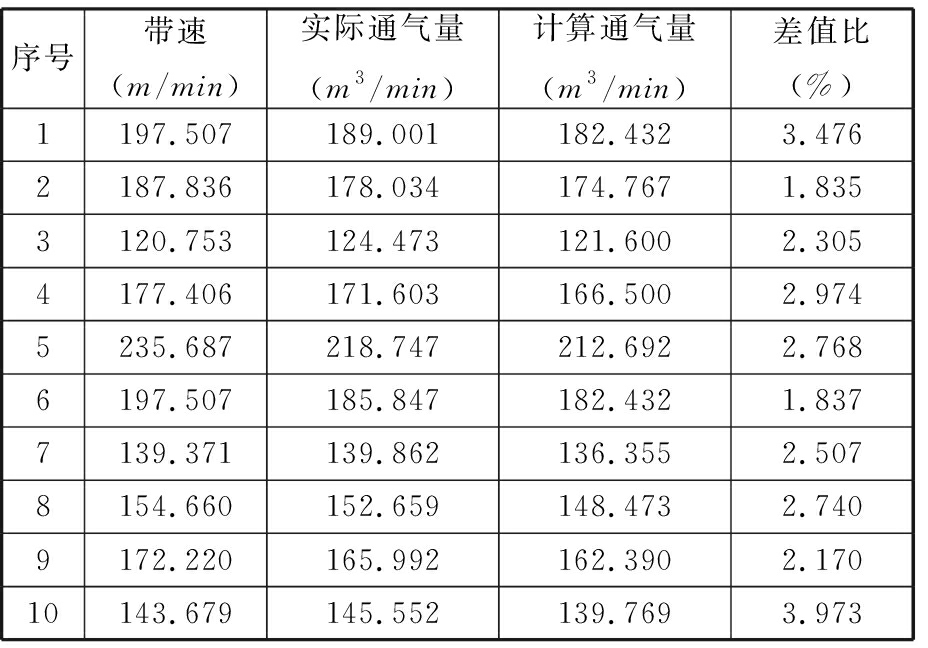
第一组数据选取生产过程中稳定状态下带宽l为1 126 mm、厚度d为0.806 mm、退火温度T1为1 073 K、不同时间段下10组不同带速的带钢,将数据代入式(13),可获得如表1所示结果。根据表1绘制同类别钢卷通气量的计算值与实际值的差值比曲线图,见图3。
表1 同规格带钢参数对比
Tab.1 Parameters comparison of the same specification strip steel
序号带速(m/min)实际通气量(m3/min)计算通气量(m3/min)差值比(%)1197.507189.001182.4323.4762187.836178.034174.7671.8353120.753124.473121.6002.3054177.406171.603166.5002.9745235.687218.747212.6922.7686197.507185.847182.4321.8377139.371139.862136.3552.5078154.660152.659148.4732.7409172.220165.992162.3902.17010143.679145.552139.7693.973
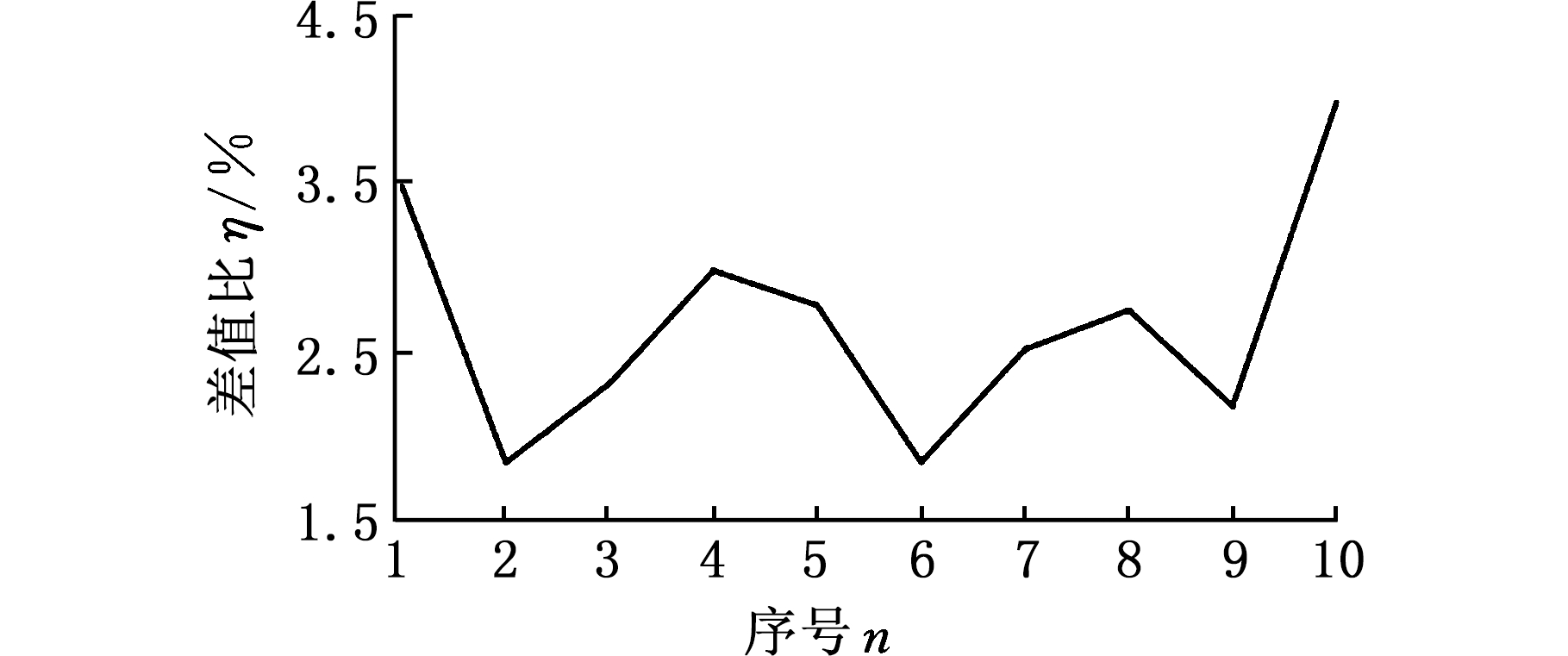
图3 同类钢卷通气量计算值与实际值的差值比
Fig.3 Difference ratios between calculated values and
practical values of the similar steel coil air flow
第二组数据选用不同带宽、带厚、带速、退火温度等参数,然后将相应参数代入式(13),结果见表2。根据表2绘制不同类别钢卷通气量计算值与实际值的差值比曲线图,见图4。从图4中可以看出误差相对较小,验证了模型的可靠性,可以用于指导后续研究分析。
表2 不同规格带钢参数对比
Tab.2 Parameters comparison of different specifications strip steel
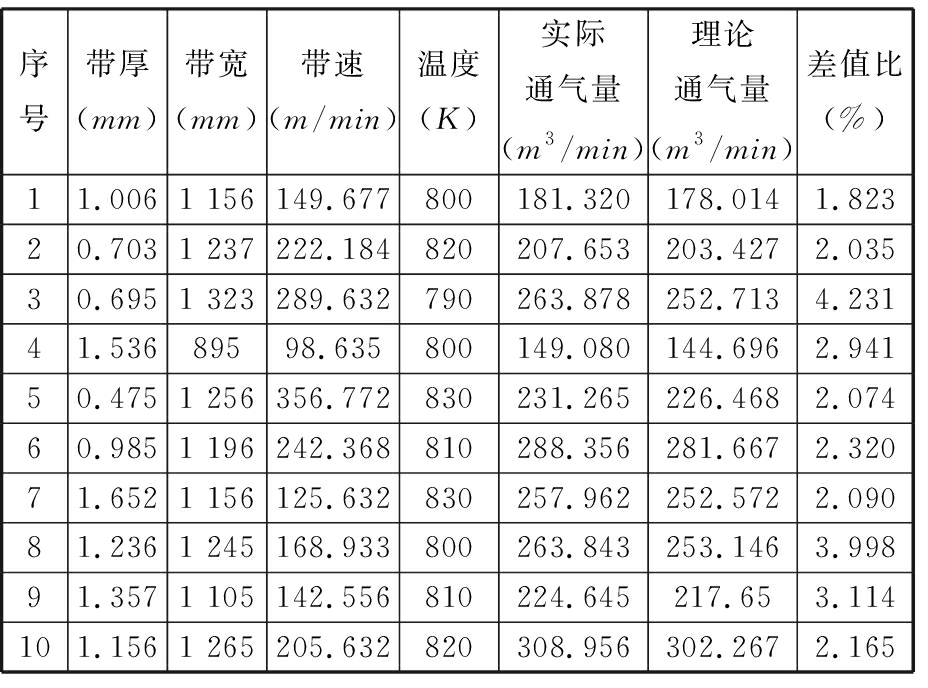
序号带厚(mm)带宽(mm)带速(m/min)温度(K)实际通气量(m3/min)理论通气量(m3/min)差值比(%)11.0061 156149.677800181.320178.0141.82320.7031 237222.184820207.653203.4272.03530.6951 323289.632790263.878252.7134.23141.53689598.635800149.080144.6962.94150.4751 256356.772830231.265226.4682.07460.9851 196242.368810288.356281.6672.32071.6521 156125.632830257.962252.5722.09081.2361 245168.933800263.843253.1463.99891.3571 105142.556810224.645217.653.114101.1561 265205.632820308.956302.2672.165
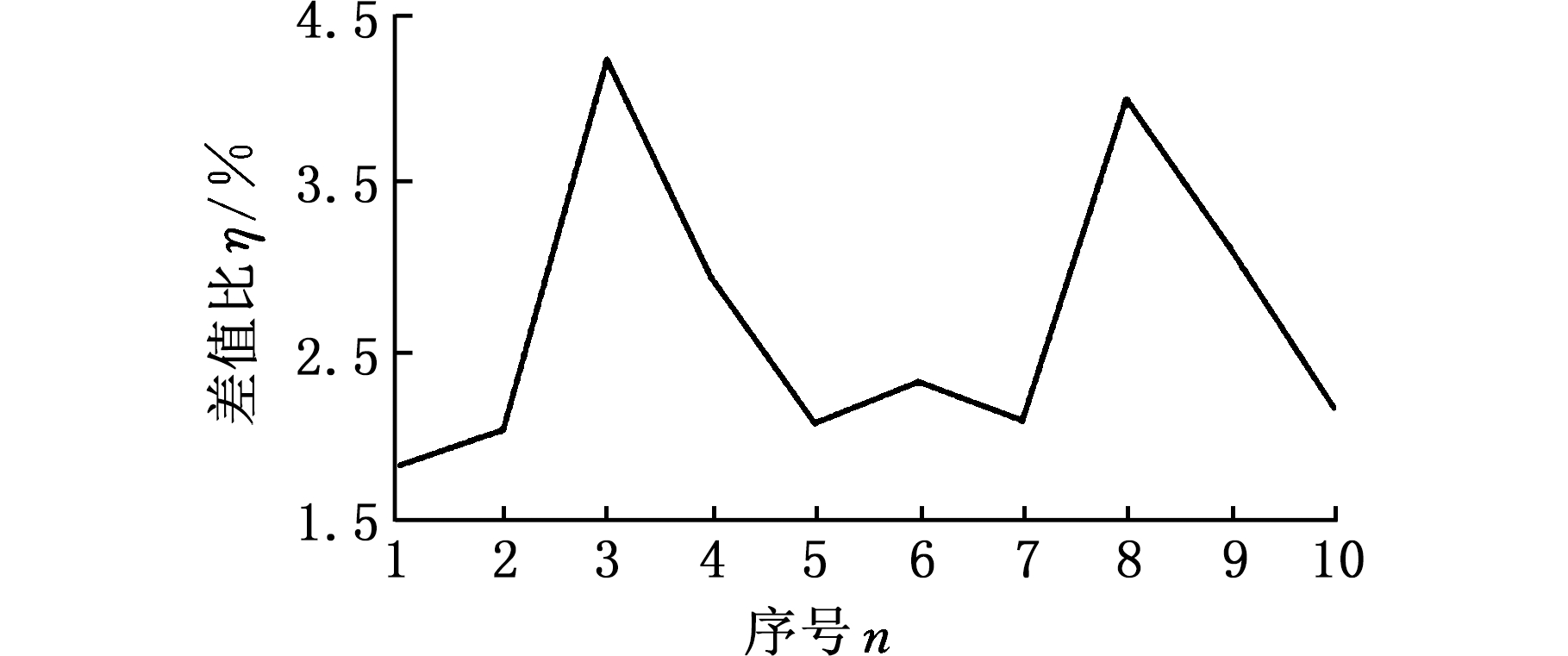
图4 不同钢卷通气量计算值与实际值的差值比
Fig.4 Difference ratios between calculated values and
practical values of different steel coil air flow
2 量子遗传算法多工艺参数优化
2.1 算法介绍
量子遗传算法是一种结合了传统遗传算法以及现代量子计算方法的概率进化算法,通过量子比特的编码形式对个体染色体进行编码操作,从而使一条染色体表达为多个状态的叠加,通过量子旋转门进行染色体的迭代和更新过程以实现目标函数的最优化求解。与传统的遗传算法相比,在种群规模较小的情况下,量子遗传算法具有更高的收敛速度和求解精度。将量子比特以及量子旋转门与传统的遗传算法相结合,形成量子遗传算法。将量子遗传算法应用于0-1背包问题的求解,得到了比传统遗传算法更为优良的结果。
量子遗传算法的流程(图5)如下:①初始化种群Q(t0),随机生成n个以量子比特位编码的染色体;②对初始种群Q(t0)中的每个个体进行一次测量,得到对应的确定解P(t0);③对各确定解进行适应度评估;④记录最优个体和对应的适应度;⑤判断计算过程是否可以结束,若满足结束条件则退出,否则继续计算;⑥对种群Q(t)中的每个个体实施一次测量,得到相应的确定解;⑦对各确定解进行适应度评估;⑧利用量子旋转门U(t)对个体实施调整,得到新的种群Q(t0);⑨记录最优个体和对应适应度;⑩将迭代次数加1,返回步骤⑤。
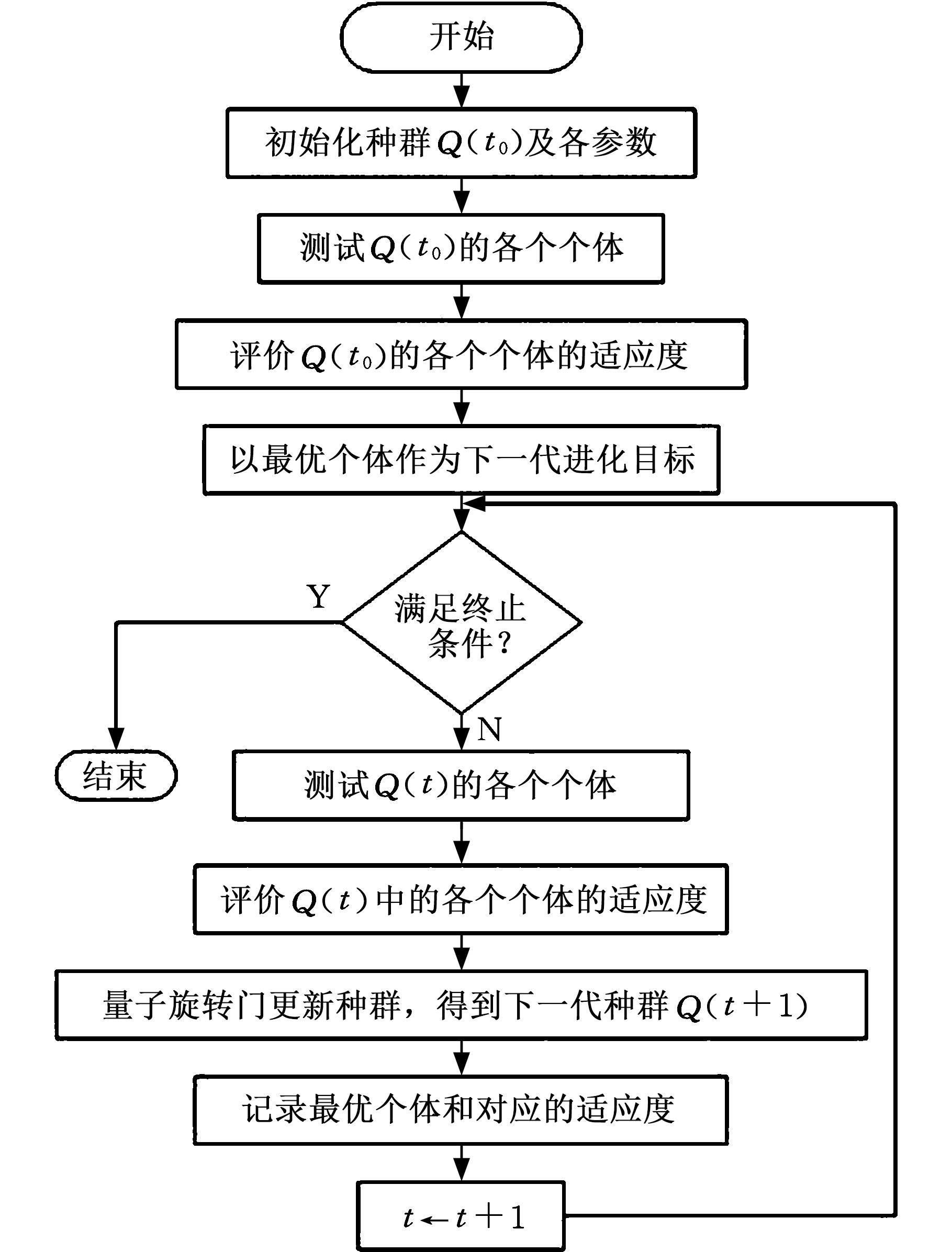
图5 量子遗传算法求解流程图
Fig.5 Quantum genetic algorithm solution
flow diagram
本文选用量子遗传算法对该模型进行优化,其中对传统的算法的改进有以下三点。
2.1.1 调整量子旋转门的旋转角
在量子旋转门的更新中,旋转角θi通常用下式表示:
θi=ks(αi,βi)
(14)
其中,(αi,βi)是两个复常数,满足
|αi|2+|βi|2=1
(15)
由s(αi,βi)这一函数表示旋转方向,逆时针以及顺时针旋转分别为+1 以及-1。
系数k的值直接影响算法整体的寻优收敛速度,当k值过大,旋转角也较大时,算法收敛过早,容易出现早熟现象。相反,当收敛速度偏慢时,则可能导致频率变低。为了解决上述问题,本文取
(16)
式中,σ为调整k的调整系数,取值0~1之间;N为种群当前迭代次数;Nmax为种群设定最大迭代次数。
2.1.2 量子位的交叉和变异操作
引入传统的交叉与变异操作可以有效避免寻优求解过程中算法容易陷入局部最优解的问题,同时还能够提高种群多样性和算法局部搜索能力。传统的交叉操作就是在个体之间暂时交换最优确定解和最优适应度值,个体接受交叉操作后,它的进化方向将受到其他个体的影响,从而获取新的进化信息。传统的变异操作通过操作染色体编码实现,互换量子比特概率幅值,可将个体的进化方向彻底反转。
单纯进行量子旋转门的旋转角改进容易陷入局部最优解,而增加变异、交叉运算会在一定程度上对这一问题进行改善。
变异方式一般有两种,一种是将种群中的某些位随机替换成其他值,另一种是将某些个体的比特位进行随机顺序重组,对变异个体的选取是按照指定的变异率从种群中随机选取。变异操作可以实现提高种群多样性和算法局部搜索的能力。
交叉算子可以使群体中的信息充分组合交换,提高搜索效率,防止陷入局部最优。进行量子交叉操作时,在种群中除了最优个体以外还按照一定的交叉概率选取若干个个体。假设共有 10个染色体,每个染色体的长度为 7,记为AiBiCiDiEiFiGi(i=1,2,…,10)。将每组染色体随机进行排序重组,如图6所示,按对角线重新排列重组,得到新的染色体个体,如A1G2B3E4B5B2D1。
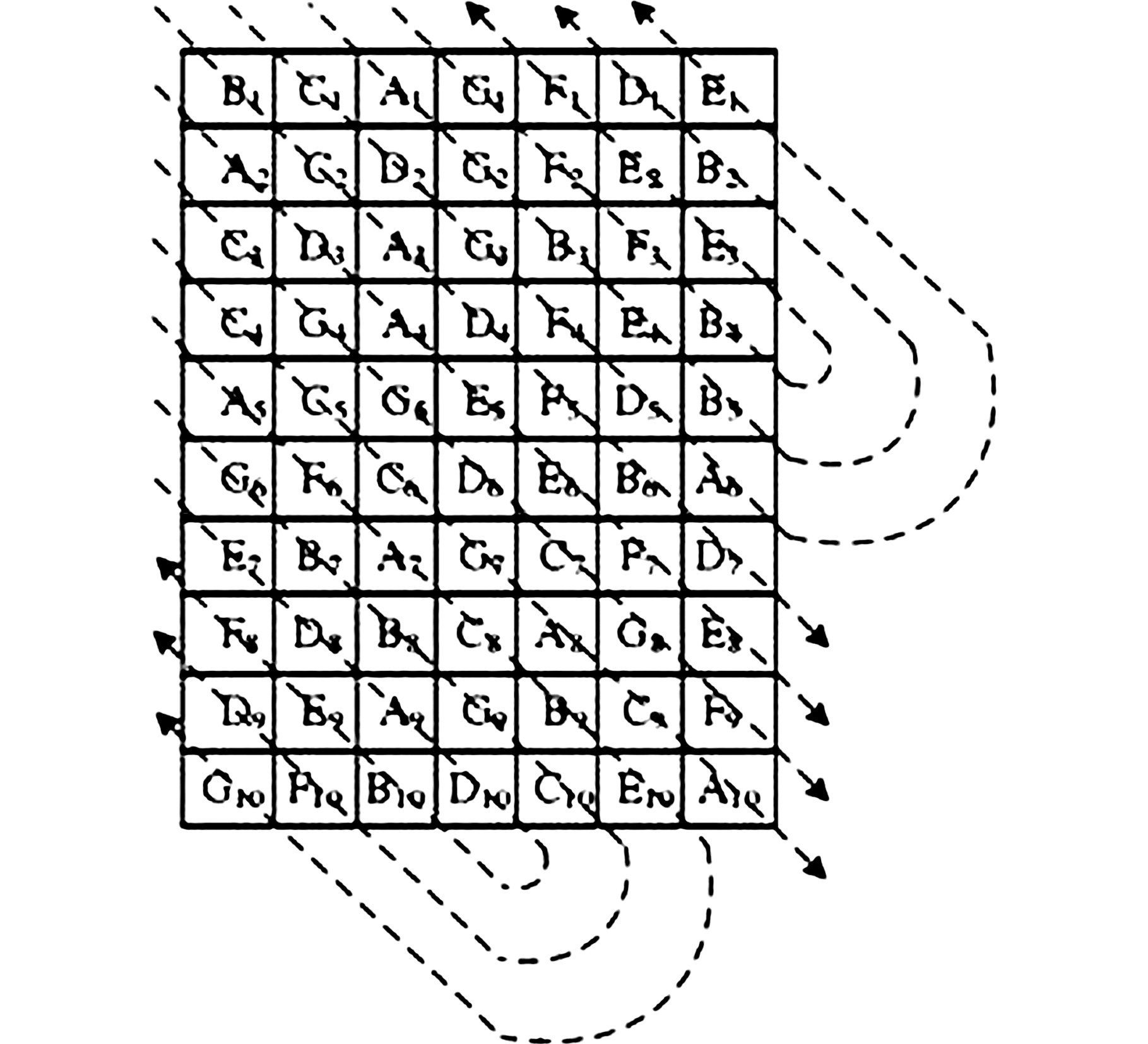
图6 量子交叉示意图
Fig.6 Schematic diagram of quantum cross
2.1.3 量子灾变操作
量子灾变可以确保在寻优过程中连续几代个体的最优适应度变化很小甚至不发生变化时,该算法陷入局部最优解的情况不会出现。为了跳出局部最优束缚,同时可以考虑仅保留少数的当前最优值个体,而其他的个体进行重新再生,以达到提高算法的全局寻优能力的目的[13]。
2.2 目标函数设计
以生产过程中吨钢能耗Qdun最低作为目标函数进行求解,因此优化的目标函数如下[14]:
f=min Qdun(v,qz,T1)
(17)
度量个体适应度的函数称为适应度函数ffit。目前适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优解,因为遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据。在适应度函数的选择中,本文选择最常见的以待求解的函数与常数的线性组合作为目标函数将其转化为适应度函数,并且以最小化为优化目标。将目标函数转化为适应度函数时,将目标函数转化为最大化问题,选用下式作为求解模型:
(18)
式中,Cmax取值为2 000。
此处引入带钢的动能进行分析,其动能消耗包含对带钢的加速与减速两部分能耗,这两部分能耗视作相等:
(19)
式中,Qdong为带钢加速及减速产生的能量消耗,kJ/min;EK为带钢达到稳定运行时的动能,kJ/min;m为单位时间内带钢质量,kg/min。
最终目标函数为
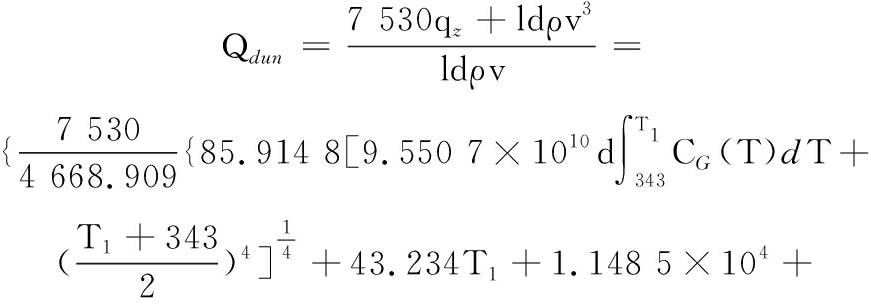
(20)
2.3 优化结果与验证
带钢相关参数如表3所示。
表3 带钢相关参数
Tab.3 Strip related parameters
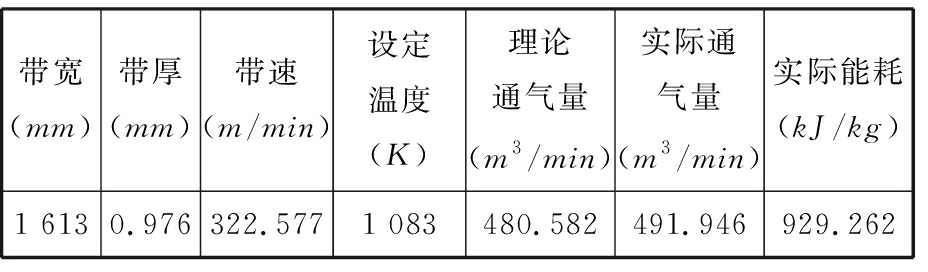
带宽(mm)带厚(mm)带速(m/min)设定温度(K)理论通气量(m3/min)实际通气量(m3/min)实际能耗(kJ/kg)1 6130.976322.5771 083480.582491.946929.262
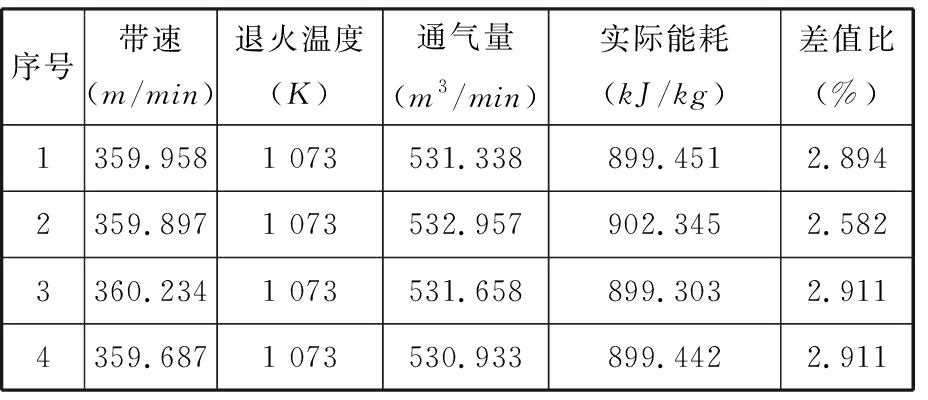
本文选取普通量子遗传算法与改进后的量子遗传算法同时进行优化。设定迭代次数为200,初始种群数为40,每个变量的二进制长度为20。两种算法迭代曲线见图7。经过优化,最终获得的带速为360 m/min,退火温度1 073 K,通气量520.924 m3/min。以此优化数据投入实际生产,获得稳定运行状态下的多组数据,并计算理论吨钢能耗与实际吨钢能耗之间的差值比,得到表4所示数据。由表4可知,通过对退火温度与速度的优化,获得最佳的通气量、温度、带速的组合,可以将吨钢能耗降低2%~3%。由此验证了通过改进量子遗传算法优化带钢生产工艺参数可以实现降低能耗的目的。
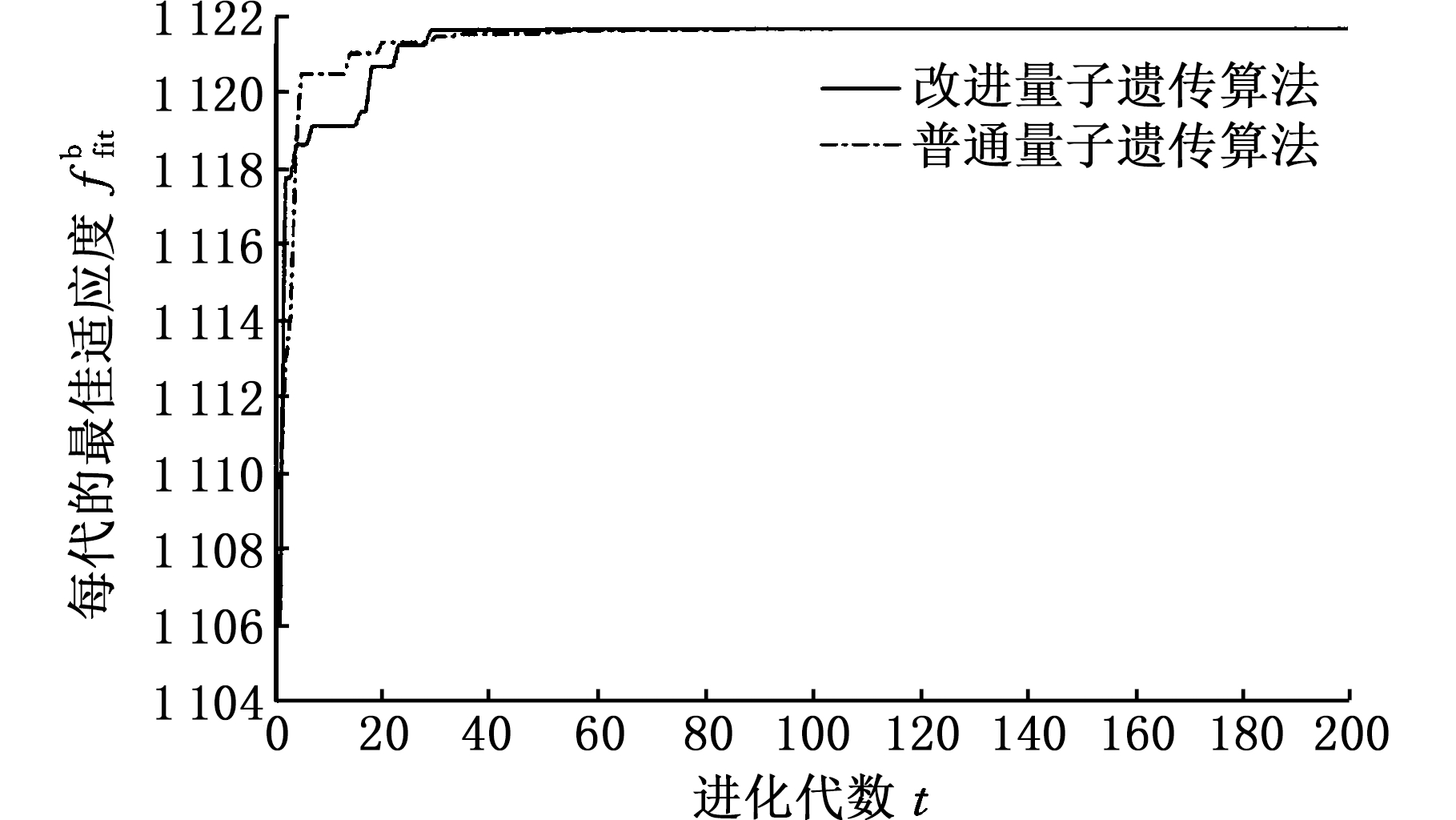
图7 改进量子遗传算法与普通量子遗传算法
迭代曲线图
Fig.7 Iterative graph of improved quantum genetic
algorithm and ordinary quantum genetic algorithm
表4 实际生产带钢数据
Tab.4 Actual production strip steel data
序号带速(m/min)退火温度(K)通气量(m3/min)实际能耗(kJ/kg)差值比(%)1359.9581 073531.338899.4512.8942359.8971 073532.957902.3452.5823360.2341 073531.658899.3032.9114359.6871 073530.933899.4422.911
3 排序优化建模
3.1 单机排序优化问题描述
根据实际生产情况,我们将连续退火生产单机排序问题概括为:从连续退火生产线的候选板卷池中按照规格、交货期等因素挑选出符合加工条件的板卷,按照生产工艺规程的要求(如温度跳跃、宽度跳跃等)将所选板卷按照一定的规则排序加工,满足设定的多个目标。
单机排序即有多个零件在一台设备上按照一定的顺序依次加工,同一时间只能完成一个设备加工。本文研究的是单机排序问题。
3.2 目标函数
根据设计方案,本文共有3个优化目标,这3个目标的实施方式如下。
3.2.1 产品规格参数跳跃平缓
生产质量控制通过优化退火温度T1、钢卷宽度l、钢卷带厚d的平滑性来实现,本文采用惩罚系数来评估参数的平滑性[15], 把3个变量变化情况转化为目标函数中的跳跃惩罚值进行求解,实现形式如下:
(21)
(22)
式中,N为钢卷数;xij为决策变量;cij为惩罚值。
模型中目标函数cij包括连退机组退火温度T1的跳跃惩罚值cijT、钢卷宽度l的跳跃惩罚值cijl以及钢卷厚度的跳跃惩罚值cijd。根据生产计划要求,3个部分的惩罚值如下所示:
退火温度T1的跳跃惩罚值
cijT=

(23)
式中,Ti为第i卷钢卷的退火温度。
式(23)表示若温度为同向跳变且不超过10 K时,设定第i卷钢卷所对应的惩罚值为0;若两次温度跳跃为反向(如前一次为升温,后一次为降温)且温度变化不超过10 K时,设定第i卷钢卷所对应的惩罚值为0.5;若温度变化在10~20 K时,设定惩罚值为0.5加温度的相对变化量;对于超过20 K的情况,设定第i卷钢卷所对应的惩罚值为2。
钢卷宽度l的跳跃惩罚值
cijl=
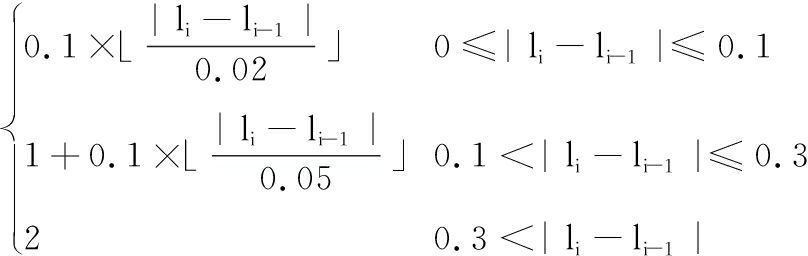
(24)
其中,⎣![]() 表示向下取整。式(24)表示若带宽阶跃在0~0.1 m以内时,第i卷钢卷所对应的惩罚值以分段函数第一个函数来计算;若带宽阶跃在0.1~0.3 m以内时,第i卷钢卷所对应的惩罚值以分段函数第二个函数来计算;若带宽阶跃超过0.3 m时,第i卷钢卷所对应的惩罚值取2。
表示向下取整。式(24)表示若带宽阶跃在0~0.1 m以内时,第i卷钢卷所对应的惩罚值以分段函数第一个函数来计算;若带宽阶跃在0.1~0.3 m以内时,第i卷钢卷所对应的惩罚值以分段函数第二个函数来计算;若带宽阶跃超过0.3 m时,第i卷钢卷所对应的惩罚值取2。
钢卷厚度d的跳跃惩罚值
cijd=
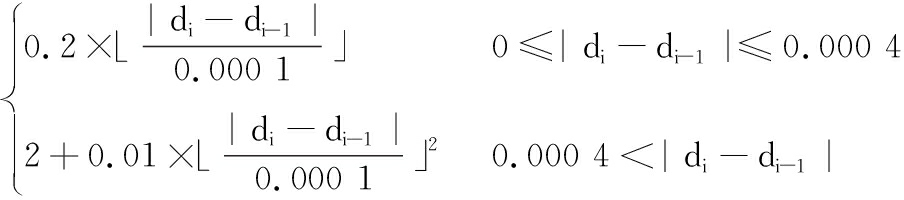
(25)
式(25)表示若带宽变化在0~0.000 4 m以内时,对应钢卷厚度阶跃惩罚值以分段函数第一个函数来计算;当宽度变化超过0.000 4m时,惩罚值通过分段函数第二个函数来计算。
总跳跃惩罚值由3个部分的惩罚值加权求和获取:
cij=α1cijT+α2cijl+α3cijd
(26)
其中,α1、α2、α3为惩罚值权重。权重值根据生产情况来设定,在本文中设定α1、α2、α3分别为0.65、0.3、0.1。
3.2.2 能耗最小化
钢卷生产过程中,动能损耗可以用对应的速度平方差来等比计算。将其转化为数学模型表示,则只需使得速度平方差的绝对值之和尽可能小:
(27)
式中,vi为第i卷钢卷带速。
3.2.3 保证交货期
这里保证交货期主要是设定交货周次。每卷钢卷都有对应的交货时间Di,交货周次分为1、2、3、4 等级,数字越大级别越低,生产时间要求也就越低,可以排在后面生产。
这里的交货期问题主要针对急单加入以及计划任务的改变所产生的订单需要提前生产的情况,由此产生了单线连续生产交货期的问题。
在大批量稳定生产过程中,不同规格钢卷生产之间的间隔时间主要与钢卷的厚度d与带速v有关:
(28)
其中,μ为一个常量,根据退火炉类型的不同而取不同值,并不影响最后优化求解,这里为了优化方便,取μ=1。
在根据优先级排序后,通过以下评估函数进行评估:
(29)
3.3 约束条件
(1)钢卷连续生产条件。第i卷钢卷生产完后,后面只能存在唯一的钢卷j,即
(30)
第j卷钢卷生产完后,后面只能存在唯一的钢卷i,即
(31)
式(30)、式(31)为流平衡约束,主要用于限定生产的过程是连续非重复的。
(2)计划规格限制条件。相邻加工的两个钢卷必须符合以下条件:
xij=1 若|Ti-Tj|≤30且
|li-lj|≤0.4且|di-dj|≤0.006
(32)
i,j∈N
4 NSGA-Ⅱ算法排序优化
本文将冷轧连退产线生产排序优化的3个目标与NSGA-Ⅱ算法结合,以此实现对生产排序最佳结果的求解。算法流程如下。
(1)算法的初始化,包括设置温度、带宽、带厚等参数的限定范围。
(2)将决策变量映射到各个染色体个体中,完成编码操作,同时随机生成满足设定约束条件的初始种群P0。
(3)将种群中个体所包含的工艺参数代入3个优化目标中,分别计算3个适应度函数的值。
(4)实施高速非支配排序操作,计算当前种群中各个个体的排序等级irank,并设目标函数个数为M(M为取值大于1的整数),种群规模设为N,具体操作如下:①初始化计数器,令j=1;②由第(2)步中计算得到的3个适应度函数的值来分析不同个体之间的支配关系,当没有达到最优个体时继续操作;③j←j+1,操作完后再次转入步骤①中操作,直到找到所有最优个体为止。
通过上述操作,找到全部等级irank=1中的最优解个体,然后从种群中移除这一部分个体。重复上述操作,在剩下的子种群中按照上述步骤执行,以此完成最优解个体的搜寻工作,直到完成所有不同等级的种群个体的最优解搜寻为止。
(5)对拥挤度id的计算。NSGA-Ⅱ算法通过拥挤度的计算能够实现全局搜索,避免陷入局域搜索产生的早熟情况,实施过程如下:①初始化操作,将所有个体所对应的拥挤度进行赋值,通常都设定id=0;②实施高速非支配排序操作,且设定两边界个体的拥挤度值Od=id=∞;③对除了边界个体的其他个体所对应的拥挤度进行计算:
(33)
式中,id为第i 点所对应的拥挤度;![]() 分别为第i+1点、第i-1点对应的第k个目标求解的目标函数值。
分别为第i+1点、第i-1点对应的第k个目标求解的目标函数值。
(6)运算操作。对比不同个体之间的id值,保存达到要求的部分,对于取值过小的部分进行剔除,同时在更广的区域内实施搜寻,扩大算法搜索范围。
(7)精英策略。将上一代种群内的优异个体取出,直接传递至下一代种群中从而产生一个具有更多优秀个体的新种群。
5 案例分析
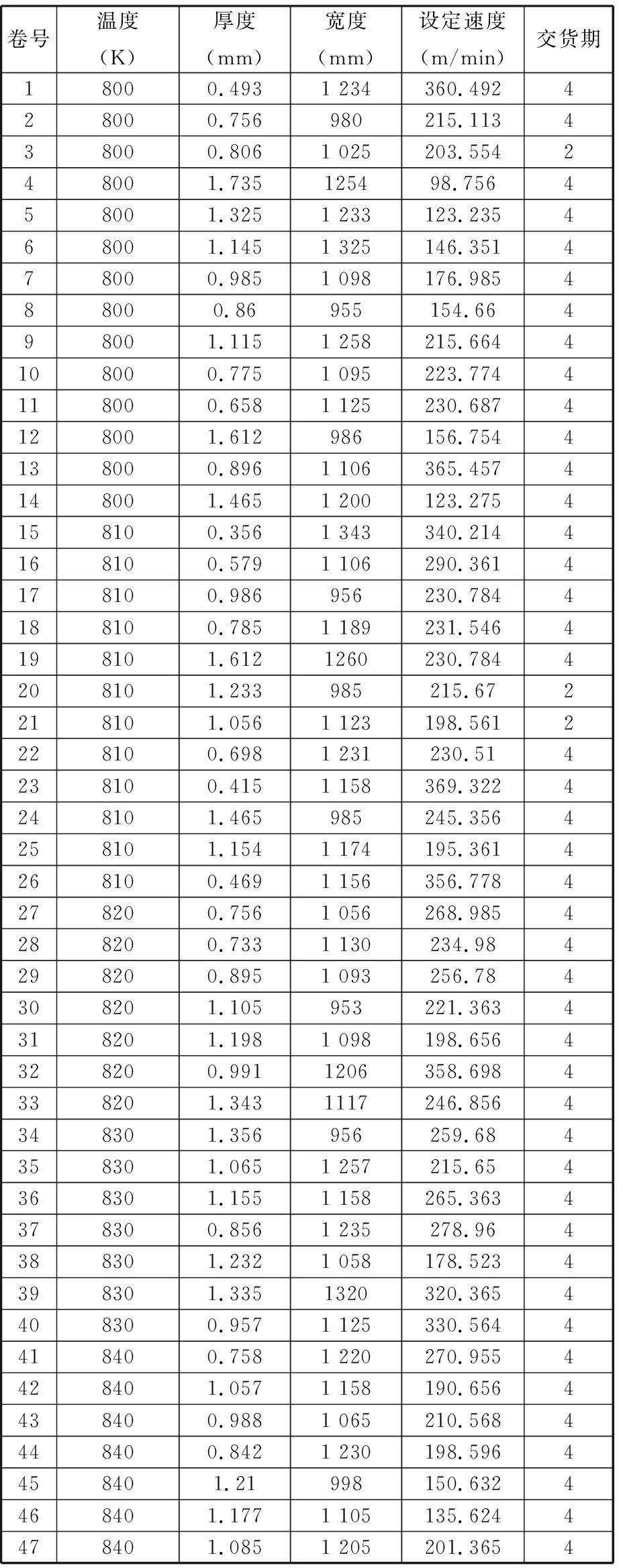
测试数据选取某钢厂某次小批量钢卷生产计划作为研究对象,钢卷总共有47组,每组10个(视为一体)。钢卷参数见表5。
该厂对产线的排序基本根据生产规格设定。排序如下:20→3→21→32→33→47→6→4→5→14→12→24→17→27→18→8→25→30→35→13→2→37→24→46→41→7→44→42→36→28→26→15→1→22→29→31→45→34→19→43→11→16→10→40→38。
引入基于多目标的精英策略NSGA-Ⅱ连退产线生产排序优化方法,3个目标函数相互制约又相互独立,不能单独从一个函数的角度来评价最优解的优劣,需要根据实际情况综合分析,最终选择了一个满足要求的解作对比。
最终优化结果如下:46→45→35→34→31→3→16→13→20→21→14→6→5→4→12→42→47→38→29→25→18→11→10→2→17→30→24→30→24→9→19→39→32→41→44→36→7→8→22→26→23→28→43→37→15→1→27→40→33。
目标函数值在优化前后的对比见表6。分析可知,通过智能算法优化得到的生产排序方式可使钢卷规格参数的平滑性更好、辅助设备的能耗更低,交货期也能满足生产所需。
6 结论
(1)本文对连退产线能量消耗情况进行了分析与优化,设计了一套用于评估吨钢能效的模型,不仅可以对能耗状态进行有效评估,还可以为多个重要工艺参数的优化分析提供参考。
表5 小批量钢卷参数
Tab.5 Parameters of the small batch steel coils
卷号温度(K)厚度(mm)宽度(mm)设定速度(m/min)交货期18000.4931 234360.492428000.756980215.113438000.8061 025203.554248001.735125498.756458001.3251 233123.235468001.1451 325146.351478000.9851 098176.985488000.86955154.66498001.1151 258215.6644108000.7751 095223.7744118000.6581 125230.6874128001.612986156.7544138000.8961 106365.4574148001.4651 200123.2754158100.3561 343340.2144168100.5791 106290.3614178100.986956230.7844188100.7851 189231.5464198101.6121260230.7844208101.233985215.672218101.0561 123198.5612228100.6981 231230.514238100.4151 158369.3224248101.465985245.3564258101.1541 174195.3614268100.4691 156356.7784278200.7561 056268.9854288200.7331 130234.984298200.8951 093256.784308201.105953221.3634318201.1981 098198.6564328200.9911206358.6984338201.3431117246.8564348301.356956259.684358301.0651 257215.654368301.1551 158265.3634378300.8561 235278.964388301.2321 058178.5234398301.3351320320.3654408300.9571 125330.5644418400.7581 220270.9554428401.0571 158190.6564438400.9881 065210.5684448400.8421 230198.5964458401.21998150.6324468401.1771 105135.6244478401.0851 205201.3654
表6 目标函数值优化前后对比
Tab.6 Comparisons of objective function values before and after optimization

f1(X)f2(X)f3(X)优化前27.194 57.8×10100优化后23.5395.1×101045.8112
(2)得到了带速、退火温度、最终煤气通入量这3个关键工艺参数的优化结果。
(3)以钢卷的实际生产质量、辅助设备的能量消耗、钢卷的交货期作为优化目标,构建了相应的求解模型,结合NSGA-Ⅱ算法完成了对连退产线生产排序的优化。
[1] 国际钢铁协会.世界钢铁统计数据[EB/OL].[2019-03-01]. https:∥www.worldsteel.org/zh/steel-by-topic/statistics/steel-statistical-yearbook/World-Steel-in-Figures.html.
World Steel Association. World Steel Statistics[EB/OL].[2019-03-01].https:∥www.worldsteel.org/zh/steel-by-topic/statistics/steel-statistical-yearbook/World-Steel-in-Figures.html.
[2] 国外钢铁业绿色节能效果窥探[EB/OL]. [2019-03-01]. http:∥news.bjx.com.cn/html/20140415/503821.shtml.
Green Energy-saving Effect of Steel Industry Abroad[EB/OL].[2019-03-01]. http:∥news.bjx.com.cn/html/20140415/503821.shtml.
[3] GAO L, HUANG J D. An Effective Cellular Particle Swarm Optimization for Parameters Optimization of a Multi-pass Milling Process[J]. Applied Soft Computing, 2012, 12(11): 3490-3499.
[4] PARK H S, TRAN N H. Development of a Smart Machining System Using Self-optimizing Control[J]. The International Journal of Advanced Manufacturing Technology, 2014, 74(9/12):1365-1380.
[5] 马峰, 张华, 曹华军. 面向低能耗少切削液的多目标加工参数优化[J]. 机械工程学报, 2017, 53(11):157-163.
MA Feng, ZHANG Hua, CAO Huajun. Optimization of Multi-objective Machining Parameters for Low Energy Consumption and Less Cutting Fluid[J]. Journal of Mechanical Engineering, 2017, 53(11): 157-163.
[6] POURSINA M, DEHKORDI N T, FATTAHI A, et al. Application of Genetic Algorithms to Optimization of Rolling Schedules Based on Damage Mechanics[J]. Simulation Modeling Practice and Theory, 2012 (22):61-73.
[7] 唐立新.基于智能优化的钢铁生产计划与调度研究[J].管理学报,2005(3):263-267.
TANG Lixin. Study on Steel Production Planning and Scheduling Based on Intelligent Optimization[J].Chinese Journal of Management,2005(3):263-267.
[8] TANG L, LIU J, RONG A, et al. An Effective Heuristic Algorithm to Minimise Stack Shuffles in Selecting Steel Slabs from the Slab Yard for Heating and Rolling[J]. Journal of the Operational Research Society, 2001, 52(10):1091-1097.
[9] WANG L, GAO X, WANG W. Dynamic Scheduling Method Based on Multi-agent for Cold Rolling Whole Line[C]∥ Proceedings of the 32nd Chinese Control Conference. Xi’an, 2013:8082-8087.
[10] VERDEJO V V, ALARCO M A P, SORLI M P L. Scheduling in a Continuous Galvanizing Line[J]. Computers & Operations Research, 2009, 36(1):280-296.
[11] 王秉铨,姜生远,王秋. 工业炉设计手册[M]. 北京:机械工业出版社,2011.
WANG Bingquan, JIANG Shengyuan, WANG Qiu. Industrial Furnace Design Handbook [M]. Beijing: Mechanical Industry Press, 2011.
[12] 张多蒙. 基于改进量子遗传算法的微电网电源经济性优化配置研究[D].沈阳:沈阳工程学院,2017.
ZHANG Duomeng. Research on Optimization and Configuration of Power Grid Economics Based on Improved Quantum Genetic Algorithm[D]. Shenyang: Shenyang Institute of Technology, 2017.
[13] 符杨,蒋一鎏,李振坤.基于混合量子遗传算法的微电网电源优化配置[J].电力系统保护与控制,2013,41(24):50-57.
FU Yang, JIANG Yiliu, LI Zhenkun. Optimization Configuration of Microgrid Power Supply Based on Hybrid Quantum Genetic Algorithm[J].Power System Protection and Control,2013,41(24):50-57.
[14] KANT G, SANGWAN K S. Prediction and Optimization of Machining Parameters for Minimizing Power Consumption and Surface Roughness in Machining[J]. Journal of Cleaner Production, 2014, 83:151-164.
[15] 李修倩,冯好娣. 最小化完成时间和加惩罚值和的批调度问题[J].计算机研究与发展,2013,50(8):1700-1705.
LI Xiuqian, FENG Haodi. The Problem of Batch Scheduling with Minimum Completion Time and Penalty Value[J]. Computer Research and Development, 2013, 50(8): 1700-1705.
 algorithm(NSGA-Ⅱ)
algorithm(NSGA-Ⅱ)