0 引言
目前,可调涡轮已被广泛应用于变几何涡轮增压技术领域。通过导叶的连续转动,可调涡轮在实现有效调控通流流量的前提下使气流以合适的攻角进入叶轮,有力推动叶轮做功[1-3]。当发动机运行在低端(低速)工况时,可调涡轮通过关闭导叶减小喷嘴喉部气体流通面积,在相同的膨胀比下气体流速增加,做功能力增强,改善发动机的低速特性;当发动机高速运行时,可调涡轮通过增大导叶开度降低涡轮及同轴压气机转速,防止增压器因超速而引发的过度增压[4-7]。在可调涡轮实际应用中,其优势主要集中在发动机低端工况,即导叶小开度工况。然而,在该工况下导叶往往具有较大的叶片安装角,使导叶压力面到吸力面之间产生较大的压差,引发强间隙泄漏损失[8]。同时,较大的导叶安装角会加剧转子进口攻角损失,使涡轮内部流场进一步恶化,降低级效率。在刹车制动工况下,可调涡轮导叶内部气体容易出现过度膨胀而产生尾缘激波。导叶间隙泄漏流和尾缘激波周期性作用于转子叶片前缘,诱导转子叶片出现高周疲劳失效现象,严重降低了可调涡轮的可靠性和使用寿命,这一问题阻碍了可调涡轮增压技术进一步推广应用。
目前,导叶间隙泄漏流和尾缘激波被重点关注和研究[9-11],研究主要集中于两者的产生和发展规律、自身结构形态和对涡轮性能的影响这一层面,同时一些文献还对两者导致的强转静干涉进行了报道。TAMAKI等[12]研究了导叶开度对间隙泄漏流动特征以及泄漏流量的影响,分析了不同导叶开度下涡轮性能降低的内流主导因素,认为在小开度下,导叶间隙泄漏流所引发的导叶和转子内部损失占据涡轮总损失的主导地位,是涡轮性能恶化的主要原因。YANG等[13]采用实验与计算流体动力学(CFD)方法对不同导叶开度下的涡轮性能进行了变工况研究,结果表明导叶间隙泄漏流对导叶内流动损失和转子叶片进口处气流的均匀性造成影响,同时间隙泄漏流随导叶开度变化呈现出不同的流动特征。HU等[14]采用CFD方法研究了导叶间隙尺寸对涡轮性能的影响,结果显示随着间隙尺寸的增大,涡轮效率不断下降。WALKINGSHAW等[15]通过试验和CFD方法研究了小开度工况下导叶间隙泄漏流对涡轮性能的影响,并分别对导叶叶根和叶顶侧存在间隙时的可调涡轮性能进行了分析,认为当导叶叶顶侧存在间隙时,涡轮性能下降更为明显,并建议在导叶设计中采用非对称间隙来降低损失。
CHEN[16]指出在发动机排气制动工况下导叶尾缘附近出现的激波周期性作用于转子叶片前缘是转子叶片发生高周疲劳的主要诱因。LEI等[17]在脉冲进气条件下针对某实际使用的可调涡轮进行了研究,重点关注了导叶尾缘激波以及转子进口攻角的变化,结果显示脉冲进气对可调涡轮性能有较大的影响,在导叶小开度下,脉冲进气严重影响了导叶尾缘激波和间隙泄漏流强度;随着涡轮膨胀比增大,尾缘激波向导叶下方移动,激波及间隙泄漏流强度增大,导叶出口流场在周向上的畸变程度加重。
传统导叶的几何形式为“整体旋转”式,导叶若实现可调,其端壁两侧不可避免地存在端壁间隙,从而产生间隙泄漏损失,影响涡轮效率。而关于新型导叶的设计目前还未见相关文献报道,相关的研究基本处于空白。因此,基于可调涡轮端壁泄漏流和导叶尾缘激波协同调控基础上的新构型导叶设计是有意义的,有必要从可调涡轮导叶新叶型设计的角度出发来评估导叶间隙泄漏流和激波协同抑制后对可调涡轮内部流动及性能的影响,为今后可调涡轮喷嘴环叶片的设计提供参考。
1 模型和数值方法
研究模型为一款柴油机用可调涡轮,导叶数目为9,转子叶片为混流形式,数目为13。图1展示了可调涡轮几何模型以及子午视图。表1给出了可调涡轮的主要几何参数。

图1 可调涡轮三维视图和子午视图
Fig.1 3D and meridian view of the variable nozzle turbine
表1 研究模型主要参数
Tab.1 Main parameters of study model

导叶数目9导叶高度(mm)10.7导叶间隙高度(mm)0.15导叶进口直径(10%, 40%,100%开度)(mm)92,98,132转子叶片数13转子进口直径(mm)70轮缘侧出口直径(mm)58转子出口高度(mm)20.5设计膨胀比2.43设计转速(r/min)11×105设计流量(kg/s)0.417
研究模型计算域网格采用IGG/AutoGrid进行划分。该拓扑结构分为5个子区域,在叶片周围采用O形网格来提高网格对叶轮几何的捕捉精度;导叶和转子叶片以及上下主流道4个区域为H形网格;导叶端壁间隙和转子叶顶间隙采用蝶型网格。
图2展示了可调涡轮转子和导叶网格,其中导叶段单通道网格节点数约为8.7×105,转子段单通道网格节点数约为4.7×105,网格总数约为1.35×106,网格最小正交角度为31.5°,最大延展比小于2.6,最大长宽比小于540。图2中温度T0和压力p0表示涡轮进气状态的参量,温度T2和压力p2表示涡轮出气状态的参量,β为导叶进气气流角,ω为转子旋转参量。
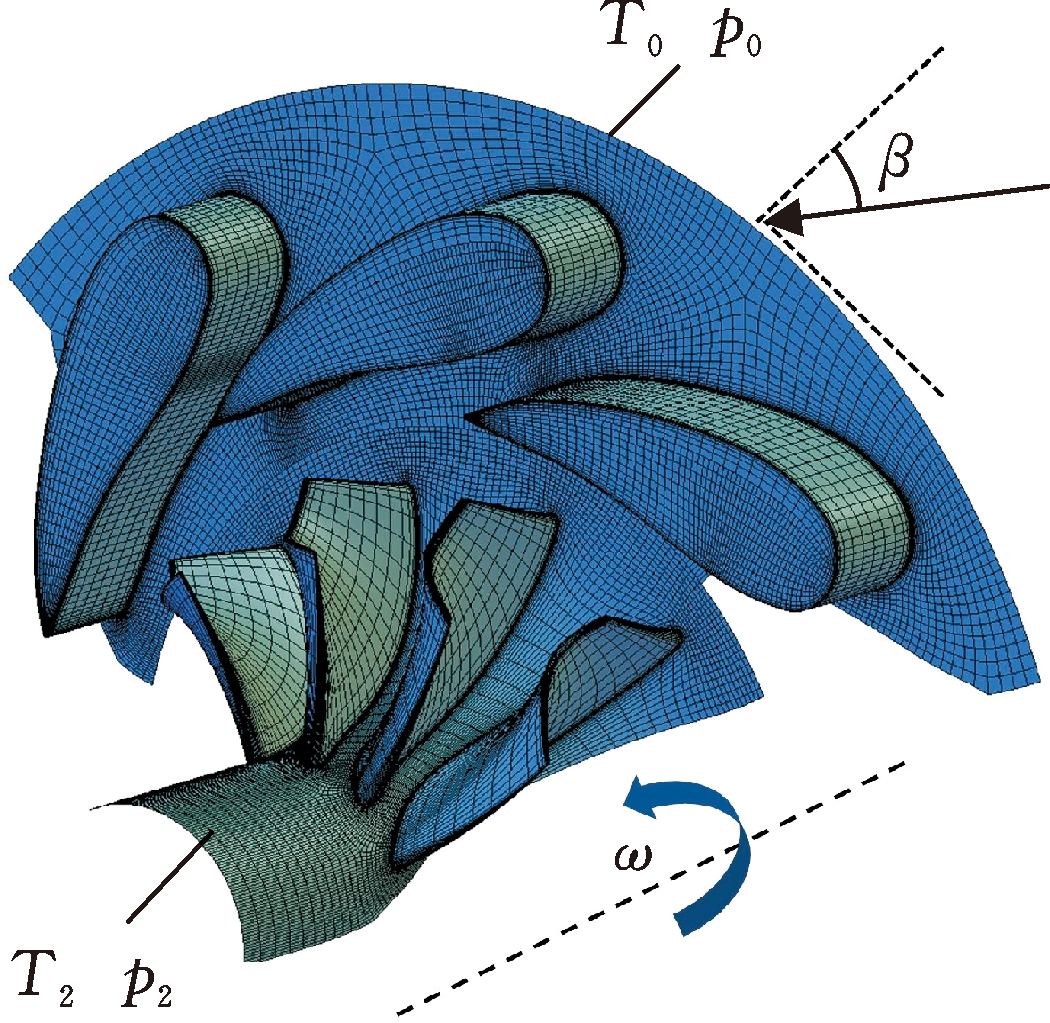
图2 研究模型导叶与转子网格
Fig.2 Mesh of the guide vane and rotor
数值计算采用NUMECA软件中FINETM/Turbo三维黏性流场计算软件,求解定常/非定常三维N-S方程,湍流模型选用S-A模型,时间项采用显式龙格-库塔时间推进法,并结合双时间步长、多重网格技术加快计算收敛速度。进口边界给定总温、总压和进口气流角度,如图2所示。其中进口气流角的大小根据气体流出蜗壳的角度计算得到。
定常计算中采用混合平面法选定转静交界面,确保气体的质量、动量和能量守恒。非定常计算中的转静交界面采用直接插值和滑移网格法。物理步长数设为120,收敛精度设为1×10-6,壁面y+值控制在3以内,如图3所示。

图3 计算域网格y+值分布
Fig.3 y+ distribution of the computational domain
网格无关性验证是数值计算中的一个重要环节。当拓扑结构确定之后,网格数量的差异会导致计算结果的偏差,也会影响计算时间,因此,合适的网格数是保证计算精度和时间的前提。本文采用单通道定常计算的方法进行网格无关性验证,如表2所示。
表2 网格无关性验证
Tab.2 Grids independence validate
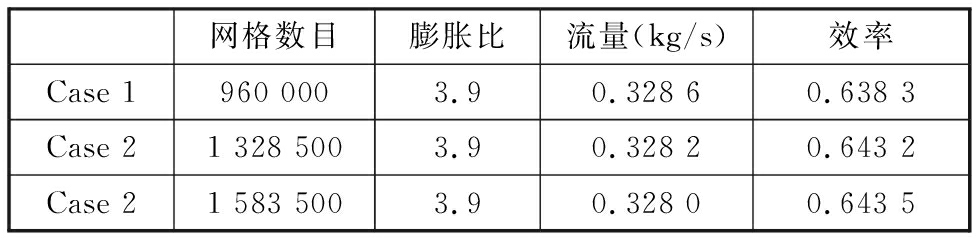
网格数目膨胀比流量(kg/s)效率Case 1960 0003.90.328 60.638 3Case 21 328 5003.90.328 20.643 2Case 21 583 5003.90.328 00.643 5
从表2中可以看出,从粗网格到中等网格,可调涡轮效率差为0.78%,而中等网格和细网格引起的效率差为0.15%,因此,为了节约计算时间,本文选用中等网格进行数值计算。
2 数值方法试验验证
通过将可调涡轮试验测试数据与数值计算结果进行比对来验证本文中所使用的数值方法的有效性。在涡轮增压器试验过程中,被测压气机的性能可直接测得,而涡轮性能则由于测功机的高成本需要通过间接的方法获得。
涡轮性能试验以获取其流量-膨胀比以及速比-效率特性为目的。流量-膨胀比特性是指涡轮相似流量随膨胀比的变化,而速比-效率特性反映了涡轮效率随速比的变化。涡轮流量可在试验中直接测出,然而,由于涡轮出口位置气体的流动非常混乱,时常伴随有大涡出现,因此其出口温度不能通过直接测量的方法获得。本研究试验台架和测试流程如图4所示,该测试方法目前被广泛应用于涡轮增压器试验[13]。

1.气源 2.空滤 3.流量计 4.电加热器 5.涡轮进口测试段
6.涡轮出口测试段 7.测试涡轮 8.润滑油测试段
9.转速传感器 10.压气机测试段 11.流量计 12.辅助增压器
13.涡轮进口静压传感器 14.涡轮进口总压传感器
15.涡轮进口温度传感器 16.涡轮出口静压传感器
17.涡轮出口总压传感器 18.涡轮出口总温传感器 19.流量计
图4 可调涡轮性能试验台架
Fig.4 Performance test bench of variable nozzle turbine
试验选择可调涡轮设计工况进行,其中涡轮转速为80 kr/min,导叶开度为80%。图4展示了测试试验台的原理以及相关测试装置的布置。空气首先通过空气滤清器,然后在进入涡轮前被加热到一定的温度,被加热的空气温度在涡轮进口位置通过电加热器调节为恒定值,然后进入涡轮测试段。同轴压气机用来吸收涡轮所做的功,通过测试相关数据来计算涡轮效率。
当被测压气机没有加载时,阀门F2和F3处于关闭状态,而阀门F4和F7打开。气体通过阀门F7进入压气机并且从F4排出,F5为微调阀门。当被测压气机开始加载时,阀门F4和F7关闭,阀门F3打开。高温气体经过阀门F2后完成加载。此外,试验中使用一个辅助增压器来消耗由被测压气机提供给气体的能量。
试验中的温度通过位于涡轮和压气机测试段的铂电阻传感器测得,铂电阻传感器的精度为±0.1%。压力数据通过压阻传感器测得,压阻传感器的精度为±0.3%。增压器转速通过外部磁感应式转速表测得,精度为±0.2%。图4所示的混合器用来使涡轮出口气流流动均匀,温度传感器只是用来监测出口气体温度,不用来进行效率计算。涡轮机的外壳和管道都是绝缘的,以减少传热损失。涡轮等熵效率η的计算公式如下:

(1)
π=p0/p2
(2)
式中,W1为涡轮实际膨胀功;W0为涡轮的等熵膨胀功;π为涡轮膨胀比;T0、T2分别为涡轮进口总温和出口总温;k为绝热指数,k=1.4;R为气体常量,R=287 J/(kg·K);cp为质量定压热容,cp=1 006 J/(kg·K);p0、p2分别为涡轮进口总压和出口静压。
本文中间接测功法是通过将压气机的实际压缩功和轴承上消耗的功相加得到。由于压气机稳定在一个转速下,同时润滑油流动稳定,故可直接通过压气机和润滑油进出口的温差计算得到涡轮效率,计算公式如下:
W1=WC,act+Woil
(3)
(4)
(5)
式中,WC,act为压气机实际压缩功; Woil为轴承的机械损失; mC为压气机质量流量; moil为润滑油质量流量; cp,air、cp,oil分别为气体和润滑油的质量定压热容。
图5a为涡轮效率特性曲线,图5b为涡轮流量特性曲线。图中,u为叶轮进口旋转线速度,c为级绝热降的理想速度。由图5可看出,数值计算数据与实验数据相符。由于数值计算忽略了漏气损失、轴承摩擦损失以及蜗壳内部流动损失,使得数值计算值比试验值略高,但误差小于3%。通过试验值与计算值的结果对比,证明了数值计算网格划分及计算方法的正确性和适用性。为保证数值计算结果的可对比性,新设计的导叶采用相同的网格数和数值计算方法来进行数值计算。

(a) 涡轮效率特性曲线

(b) 涡轮流量特性曲线
图5 涡轮性能曲线实验值与计算值对比
Fig.5 Comparison of the test and CFD results
3 导叶间隙对原始模型性能影响分析
间隙泄漏流在导叶小开度下对可调涡轮性能影响较大,由于分体滑动导叶的设计是在对间隙泄漏流抑制的基础上进行的,因此在导叶设计前需要对所泄漏损失进行评估。选择原始模型10%和80%两个代表性的导叶开度,进行导叶有端壁间隙和无端壁间隙下的定常计算。为了消除导叶主控几何参数(如导叶出口角、转静间距)的影响,无端壁间隙模型是在原始模型基础上直接去掉间隙获得的。
图6展示了两种模型的性能曲线,由图6a可知在80%导叶开度下两种模型的流量差别很小,有间隙模型流量略高于无间隙模型;而在10%开度下,由于导叶间隙作用的增强,两者的流量随膨胀比差别不断增大。图6b展示了两种模型的速比-效率曲线,分析可知两种模型效率差在10%开度下随着速比的增加呈现出先增大后减小的趋势,两者峰值效率差别为20%。在80%开度下,两模型的峰值效率差别为5%,效率差同样随速比的增大出现先增加后减小的情况。文中对比结果和HU等[14]的结果具有一致性,即导叶间隙泄漏流在小开度下对涡轮性能影响程度高达20%。

(a) 涡轮流量特性曲线

(b) 涡轮效率特性曲线
图6 导叶有间隙和无间隙下的性能曲线对比
Fig.6 Comparison of performance curves of guide
vane with and without clearance
对比可知,通过抑制导叶间隙泄漏流来提高涡轮性能的方法主要以导叶小开度和中间开度下的效率提升为目标,但同时需保证大开度下涡轮性能不降低。如同时兼顾导叶大开度下的涡轮效率提升,则需综合考虑导叶型线损失、尾迹损失等主控因素。
4 分体滑动导叶部分参数设计原则
分体滑动导叶的提出是基于导叶间隙泄漏流和尾缘激波协同抑制这一原则而进行的。分体滑动导叶的设计原则主要有以下两方面:第一,导叶在全开工况下须满足发动机最大排气量,并且在各开度下具有与原始导叶同等的流量调节能力;第二,在涡轮所有运行工况下分体滑动导叶较原始模型性能均应有所提高,并在导叶小开度下大幅度提高可调涡轮效率。同时,设计的分体滑动导叶激波强度较原始导叶应得到有效抑制。
在充分考虑上述两原则后,所构思的分体滑动导叶结构如图7所示。该导叶由两个相互独立的叶型构成,其中,固定导叶F在叶根和叶顶侧不存在间隙,因此无间隙泄漏流产生;滑动导叶S作为关键的调节部件,通过沿滑动半径上下滑动的方式来实现导叶的通流面积调节。为防止分体滑动导叶在调节过程中出现受热膨胀卡滞现象,滑动导叶S采用与原始导叶尺寸相同的端壁间隙。

图7 分体滑动导叶叶型
Fig.7 Shape of the split sliding guide vane
在分体滑动导叶的设计过程中,导叶S和导叶F的滑动轨迹应为同心圆弧,以确保导叶S在滑动过程中不被卡滞。考虑到分体滑动导叶在高温环境中的可靠性,导叶S和导叶F采用与原始导叶相同的尾缘直径。
分体滑动导叶叶片数的选取主要遵循两点:第一,导叶与转子叶片数无公约数,以防止转子叶片出现共振;第二,由于导叶叶片数直接影响叶型损失和尾迹损失,因此在设计中应尽可能减少叶片数。本设计中分体滑动导叶叶片数与原始导叶数目相同。
5 数值计算及结果分析
5.1 原始模型和分体滑动模型性能对比
将原始模型和分体滑动模型分别在10%、40%和100% 3个代表性开度下进行定常计算。两种模型在3个开度下的流量特性曲线和效率特性曲线见图8。由图8a可知,两种模型所对应的流量曲线随涡轮膨胀比增大能很好地贴合,表明分体滑动导叶在10%和100%两个极端开度下能满足发动机排气需求,因此设计的分体滑动导叶与原始导叶具有相同的流量调控能力。
对比两者在图8b中的效率特性曲线可以看出:在10%开度下,分体滑动导叶可提高10%的涡轮峰值效率;在40%开度下,分体滑动模型的峰值效率比原始模型提高了约3%,效率提高幅度较10%开度降低;在100%开度下,分体滑动模型峰值效率只比原始模型提高1%,在其他速比点两种模型的效率基本相同。这从另一方面说明了通过抑制导叶间隙泄漏而取得的效率收益随导叶开度增大而减小,结果表明设计的分体滑动导叶在100%开度下通过抑制间隙泄漏流而提高的效率大于导叶自身型线引发的流动损失。
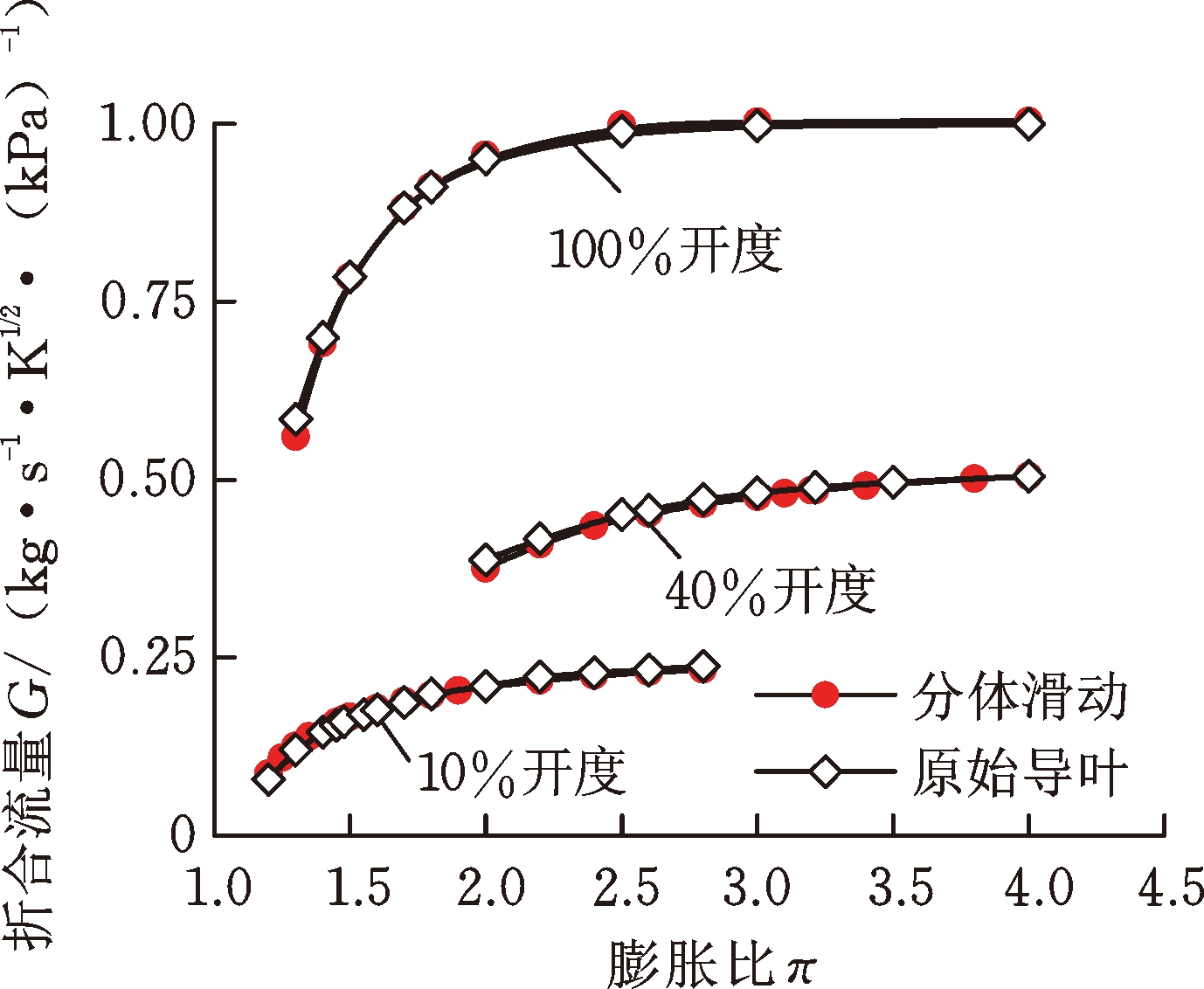
(a) 两种模型流量特性

(b) 两种模型效率特性
图8 两种模型在3个开度下的流量和效率特性曲线
Fig.8 Flow and efficiency characteristic curves of two
models under three opening conditions
通过对比可知分体滑动导叶在10%开度下可大幅度提高涡轮性能,因为原始叶型是Honeywell公司优化多次并成功应用于柴油机用可调涡轮增压器多年的叶型[7,14,17],因此对该叶型性能的提升使分体滑动导叶的应用具有普适性。
为量化两种模型导叶内部流动损失,使用总压损失系数来对比两种模型在3个代表性开度下导叶内的损失分布。图9展示了两种模型导叶出口总压损失系数沿导叶相对高度分布规律。分析可知,两种模型在3个开度下导叶端壁两侧的总压损失系数大于其他叶高位置。在10%开度下,从叶根到40%叶高和从约60%叶高到叶顶位置,在40%导叶开度下,从叶根到约20%叶高和从约90%叶高到叶顶位置,以及在100%导叶开度下,从叶根到约10%叶高和从约95%叶高到叶顶位置,由于弱化了导叶间隙泄漏流,分体滑动模型导叶总压损失系数小于原始模型。随着导叶开度增大,导叶间隙泄漏流影响的范围逐渐减小,因此分体滑动模型和原始模型在叶根和叶顶附近的总压损失系数的差别随导叶开度逐渐减小。

(a) 10%导叶开度

(b) 40%导叶开度

(c) 100%导叶开度
图9 导叶出口总压损失系数分布
Fig.9 Distribution of total pressure loss coefficient
at guide vane outlet
导叶中间叶高位置的总压损失分布与端壁位置呈现出不同的规律,由于不受导叶间隙泄漏流影响,中间叶高位置总压损失主要归因于导叶尾迹。由于分体滑动导叶具有两个尾缘,其尾迹损失比原始导叶有所增大,因此在中间叶高位置,分体滑动导叶的总压损失系数在不同开度下均高于原始模型。随着开度增大,原始模型和分体滑动模型的总压损失系数差别也逐渐增大,主要原因是导叶尾迹随开度的增加对可调涡轮的影响程度逐渐增强,分体滑动模型的“双尾缘”结构会造成更多的尾迹损失。结果表明了在导叶小开度下,间隙泄漏流造成的损失占据主导地位,而叶型损失、尾迹损失等占据次要地位。
虽然在导叶大开度下分体滑动模型总压损失在中间叶高范围大于原始模型,然而通过分析可以发现,两种模型在中间叶高位置的总压损失系数的值与端壁相比是非常小的,因此分体滑动导叶通过削弱间隙泄漏流来提高涡轮效率所取得的收益可完全弥补因其几何结构所造成的损失。
通过上述分析,分体滑动导叶对于间隙泄漏流的抑制是十分有效的,但同时也会因为叶型不光顺、“双尾缘”等几何结构造成额外的流动损失。因此,如何有效地平衡通过抑制导叶间隙泄漏流而带来的收益和因其自身几何因素造成的流动损失是在分体滑动导叶设计过程中需要着重考虑的问题。
5.2 两种模型导叶尾缘激波分析
为分析分体滑动模型因导叶尾缘激波而导致的转子叶片可靠性问题,将其尾缘激波与原始模型进行对比,主要关注两个方面:一是两种模型导叶尾缘激波最大值;二是导叶尾缘激波在转子叶片前缘位置的强度。
图10和图11分别定性和定量对比了原始模型和分体滑动模型在40%开度下导叶尾缘激波最大强度以及转子前缘激波强度,激波强度用周向静压梯度(Grad SP)来表示,结果为非定常计算时均值。从图10a中可以看出两种模型导叶尾缘均存在高静压梯度突变区,因此两种模型都存在导叶尾缘激波。通过对比图11a中两种模型静压梯度最大值可以发现两者相差不大,分体滑动模型相比于原始模型而言静压梯度最大值只降低了约10%。通过图10b和11b综合分析可知,两种模型导叶尾缘激波在转子前缘的强度是不同的,表现为原始模型转子前缘静压梯度值与最高值相差不大,而分体滑动模型转子前缘静压梯度值比最大值降低了约60%,说明对于分体滑动模型而言,导叶尾缘激波在转子叶片前缘的作用强度远低于原始模型。

(a) 导叶尾缘静压梯度最大值

(b) 转子叶片前缘静压梯度值
图10 两种模型导叶尾缘激波和转子前缘激波分布
Fig.10 Shock distribution at guide vane trailing edge
and rotor leading edge of the two models
5.3 两种模型转静干涉强度分析
由于转子和导叶之间的相对运动,导叶尾缘激波和间隙泄漏流会周期性作用于转子叶片,迫使其出现谐共振。分体滑动导叶的设计在一定程度上改善了上游气体的流动状况,从而对下游转子叶片产生积极的影响。
图12展示了原始模型和分体滑动模型在10%和40%导叶开度下转子叶片表面量纲一静压均方根(RMS)值分布,用来反映转子叶片表面静压波动随机分布情况。对比可知在两个开度下,转子叶片高静压波动最大值出现在转子前缘位置,对应于可调涡轮在实际运行中容易发生高周疲劳断裂的位置。从叶片前缘到尾缘静压RMS值逐渐降低。图12a展示了两种模型在10%导叶开度下的静压RMS值分布,两种模型在轮缘和轮毂侧的高静压波动区主要是由导叶间隙泄漏流引发的,而中间位置主要是由导叶较大的安装角而导致的非匹配攻角所导致的。由于分体滑动模型导叶间隙泄漏流的减弱,故在轮缘、轮毂侧高静压波动区的面积和强度较原始模型而言都有所减小。分体滑动模型在转子叶片中间位置的高静压波动区域的减小则主要得益于导叶和转子间距增大。

(a) 两种模型静压梯度最大值
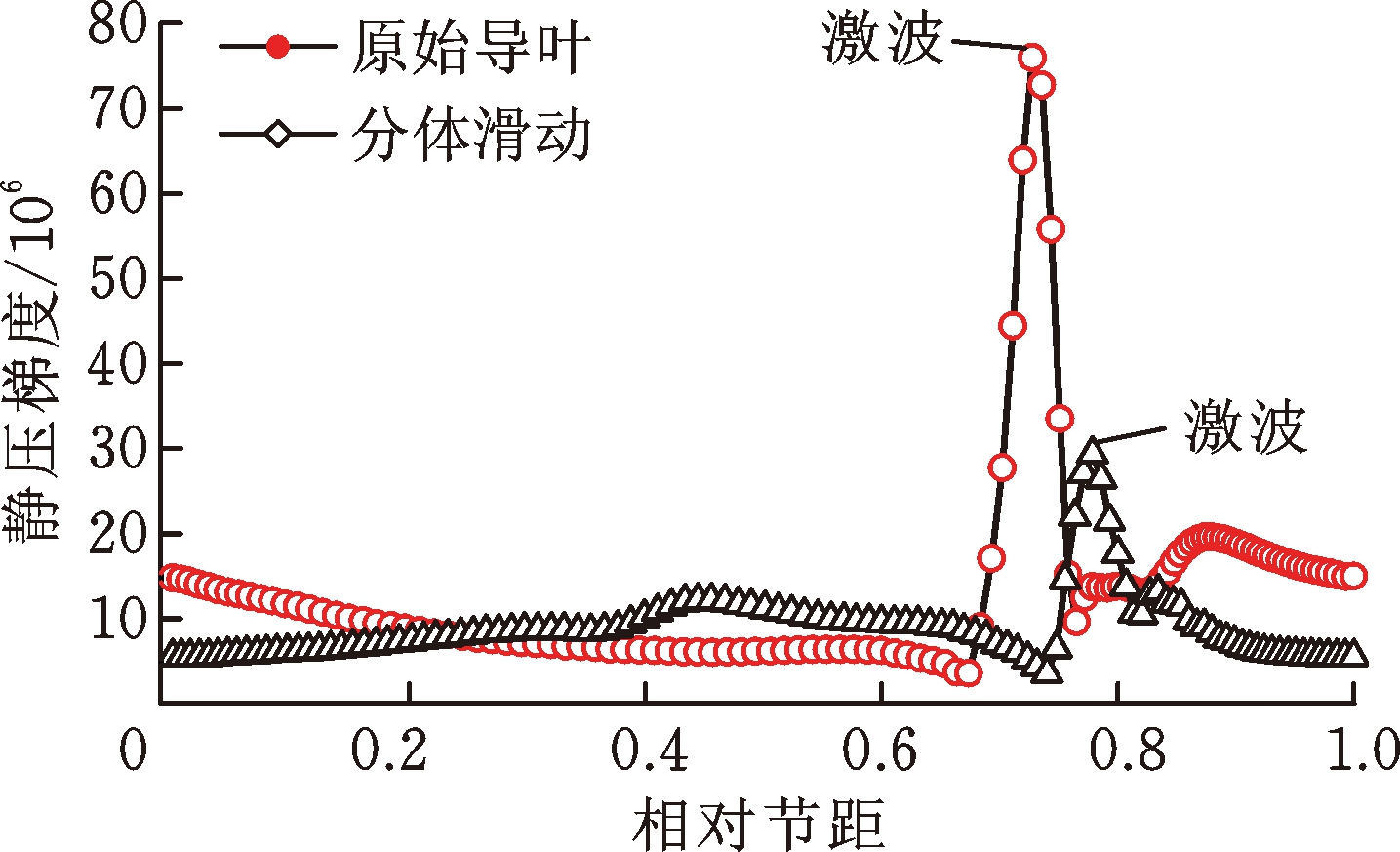
(b) 转子前缘静压梯度值
图11 两种模型导叶尾缘激波最大值和转子前缘激波强度
Fig.11 The maximum shock value of guide vane trailing
edge and the intensity of shock at the leading edge
of rotor in the two models
对比图12b所展示的50%导叶开度下两种模型转子叶片表面静压RMS值分布可知,其分布规律和10%导叶开度相似。同理,分体滑动模型叶片前缘高静压波动强度相比于原始模型而言有所降低。由于分体滑动模型导叶间隙泄漏流的减弱,故在轮缘和轮毂侧高静压波动区的面积和强度较原始模型而言都有所减小;而中间叶高位置静压RMS值的减小主要是由其激波强度降低所导致的。分体滑动导叶在不同导叶开度下均有效降低了转子叶片因导叶间隙泄漏流和导叶尾缘激波而引发的强迫相应强度,在提高了可调涡轮效率的基础上同时增强了转子叶片的可靠性,证明分体滑动导叶的设计是成功的。

(a) 10%导叶开度
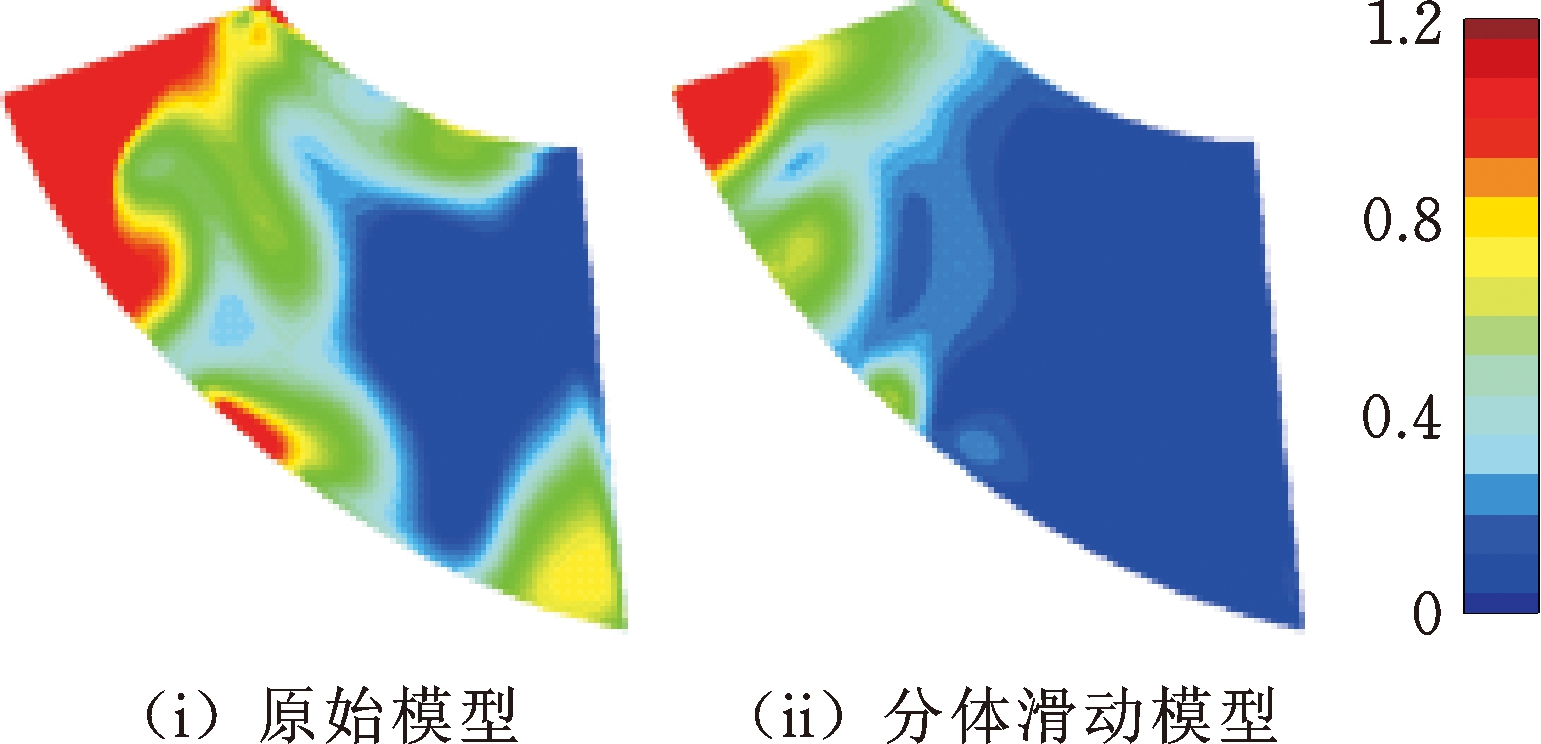
(b) 40%导叶开度
图12 两种模型转子叶片吸力面静压均方根值分布
Fig.12 The RMS value distribution of static pressure on
suction surface of rotor blades in two models
6 结论
针对某可调涡轮在导叶小开度下低效强激波特性,分析了原始导叶和分体滑动导叶两种模型气动性能并对激波和转子载荷波动特征进行了对比研究,主要结论如下:
(1)分体滑动导叶固定部分不存在端壁间隙,在10%开度下导叶间隙泄漏量降低了约65%,涡轮效率提高了10%。在100%导叶开度下,分体滑动导叶的峰值效率在满足可调涡轮流量的基础上提高1%,说明分体滑动导叶的设计是较为成功的。
(2)分体滑动导叶可有效抑制间隙泄漏流强度,但同时会因叶型不光顺、“双尾缘”等因素造成额外的流动损失,因此,有效平衡通过抑制导叶间隙泄漏流而带来的效率收益和因其自身几何因素造成的流动损失是在分体滑动导叶设计过程中需要着重考虑的问题。
(3)由于分体滑动导叶间隙泄漏流和尾缘激波的削弱,转子叶片最大载荷和载荷波动强度在10%和40%开度下均低于原始模型,因此减小了转子叶片发生高周疲劳失效的风险。
[1] MATSUNMOTO K, JINNAI Y. Development of Variable Geometry Turbocharger for Diesel Passenger Car[C]//The 6th International Conference on Turbocharging and Air Management System. London, 1988: 329-346.
[2] OKAZAKI Y, MATSUDAIRA N. A Case of Variable Geometry Turbocharger Development[C]//The Third International Conference on Turbocharging and Turbochargers. London, 1986: 191-195.
[3] 马朝臣, 朱庆, 杨长茂, 等. 涡轮调节方式对增压柴油机匹配性能的影响[J]. 内燃机学报, 2000, 18(2): 165-167.
MA Chaochen, ZHU Qiang, YANG Changmao, et al. Effect of Turbine Adjustment Methods on Matching Performance of Turbocharged Diesel Engine[J]. Transactions of Csice, 2000, 18(2): 165-167.
[4] BAINES N C. Fundamentals of Turbocharging[M]. White River Junction, Vermont: Concepts NREC, 2005.
[5] MORI I, KIYOHIRO S, KOICHI M, et al. A Study on Improving Fuel Consumption of Heavy-Duty Diesel Engine Specifically Designed for Long-Haul Trucks on Highway[J]. SAE Technical Paper, 2015-01-1256.
[6] WATSON N. Turbocharging the Internal Combustion Engine[M]. London: The Macmillan Press Ltd., 1982.
[7] LIU Y, YANG C, YANG D, et al. Investigations on the Aerodynamic Characteristics and Blade Excitations of the Radial Turbine with Pulsating Inlet Flow[J]. International Journal of Turbo & Jet-Engines, 2016, 33(1): 69-80.
[8] LIU Yinhong, YANG Ce, QI Mingxu, et al. Shock, Leakage Flow and Wake Interactions in a Radial Turbine with Variable Guide Vanes[J]. ASME Paper, 2014, No. GT2014-25888.
[9] SPENCE S W T, DORAN W J, ARTT D W. Experimental Performance Evaluation of a 99.0 mm Radial Inflow Nozzled Turbine at Larger Stator-rotor Throat Area Ratios[J]. Proc. IMechE, Part A, 1999,213: 205-218.
[10] DORAN W J, SPENCE S W T, ARTT D W. Experimental Performance Evaluation of a 99.0 mm Radial Inflow Nozzled Turbine with Varying Shroud Profiles[J]. Proc. IMechE, Part A, 2001,215: 267-280.
[11] ALISTER S, SPENCE S W T, ARTT D W, et al. Experimental and Numerical Investigation of Varying Stator Design Paprameters for a Radial Turbine[J]. ASME Paper, 2006, No. GT2006-90152.
[12] TAMAKI H, GOTO S, UNNO M, IWAKAMI A, et al. The Effect of Clearance Flow of Variable Area Nozzle on Radial Turbine Performance[J]. ASME Paper, 2008, No. 2008-GT-50461.
[13] YANG Dengfeng, YANG Ce, LAO Dazhong, et al. A Detailed Investigation of a Variable Nozzle Turbine with Novel Forepart Rotation Guide Vane[J]. Proc. IMechE, Part D: Journal of Automobile Engineering, 2019, 233(4): 994-1007.
[14] HU L J, YANG C, SUN H, et al. Numerical Analysis of Nozzle Clearance Effect on Turbine Performance[J]. Chin. J. Mech. Eng., 2011, 24(4): 618-625.
[15] WALKINGSHAW J, SPENCE S, EHRHARD J, et al. A Numerical Study of the Flow Fields in a Highly Off-design Variable Geometry Turbine[J]. ASME Paper, 2010, No. GT2010-22669.
[16] CHEN H. Turbine Wheel Design for Garrett Advanced Variable Geometry Turbines for Commercial Vehicle Applications[C]//Proc. 8th International Conference of Turbochargers and Turbocharging. London, 2006: 317-327.
[17] LEI Xinguo, QI Mingxu, SUN Harold, et al. Investigation on the Shock Control Using Grooved Surface in a Linear Turbine Nozzle[J]. Journal of Turbomachinery, 2017, 139(12): 121008-121008-12.
