0 引言
内燃机是一种往复式动力机械,通过振动信号对其进行故障诊断是一种直接、有效的方法,但其结构复杂、运动部件众多,振动信号是典型的多分量、非平稳信号,容易导致故障信息被淹没,因此,如何对振动信号进行处理以提取其故障信息是一个关键问题。
时频分析方法通过将一维的振动时域信号映射到二维时频面,能够提供足够的信号故障分类信息[1-2],研究人员对此开展了大量研究。文献[3]将短时傅里叶变换引入内燃机故障诊断,有效刻画了振动信号时频特性。文献[4]采用变分模态分解(variational mode decomposition, VMD)方法对故障信号进行联合时频分析,显著提高了故障特征提取的准确率。文献[5]将图像分割理论引入柴油机故障诊断中,该方法能够有效提取振动信号图像几何特征参数。文献[6]提取了时频图像的三维重心和信息熵来识别设备状态。
针对内燃机振动信号中故障信息弱、时频分辨率低等困难,本文引入玛基诺-希尔时频分布(Margenau-Hill time-frequency distribution,MHD)分析方法对内燃机振动信号进行时频表征。MHD属于Cohen类时频分布,双线性核函数的引入使信号在时频平面产生了严重的交叉干扰项,导致时频面出现“虚假信号”,从而影响后续识别诊断的精度。鉴于此,本文提出一种基于阈值筛选的变分模态分解(VMD)算法,先将振动信号分解为k个单分量模态信号,对单分量模态信号先分别进行时频分析,再将结果进行线性叠加得到原始信号的时频图像,该方法能够有效抑制交叉干扰项的产生。对于时频图像的特征提取,非负矩阵分解(non-negative matrix factorization,NMF)方法取得了良好的效果,但是其改进算法——局部非负矩阵分解(local non-negative matrix factorization,LNMF)的结果具有更好的稀疏性[7],本文采用LNMF进行特征提取。同时,为了进一步提高故障诊断的准确率,本文还提出一种将振动信号的时频特征与信号传统的时域参数特征进行特征融合的方法,并通过改进粒子群优化(particle swarm optimization,PSO)算法对支持向量机(support vector machine,SVM)参数进行优选,通过对内燃机气门间隙故障8种工况下实测信号进行识别诊断试验,证明了本文所提方法的优越性。
1 振动信号时频分析和时域参数特征
1.1 基于阈值筛选的VMD算法
2014年,DRAGOMIRETSKIY等[8]提出一种VMD自适应信号处理新方法。VMD算法在获取本征模态函数(intrinsic mode function,IMF)时摆脱了经验模态分解 (empirical mode decomposition,EMD) 算法所使用的循环筛分剥离的信号处理方式,而是将信号分解过程转移到变分框架内,通过搜寻约束变分模型最优解来实现信号自适应分解,每个IMF的频率中心及带宽在迭代求解变分模型的过程中不断更新,最终可根据实际信号的频域特性完成信号频带的自适应剖分,得到若干窄带IMF。算法的详细步骤可参考文献[8-9]。
经研究发现,用VMD算法对信号进行分解时需要预设IMF的个数k,如果k取值过大,会造成信号的过分解,产生模态混叠;如果k取值过小,则会导致信号分解不充分,导致时频表征时干扰项过多。为了寻找合适的k值,一般的处理方式是“观察法”,即预先设定一个大概的k值对信号进行分解,观察各个IMF的中心频率,如果中心频率相差较大,则令k←k+1继续分解,直至出现中心频率相近的IMF。为解决该方法易受主观因素影响的不足,本文提出了一种基于阈值筛选的k值确定方法,其基本思想是:如果振动信号出现了过分解,则分解出的IMF会出现频率成分互相重叠的情况,此时这两个分量信号的互相关系数会比两个频率成分完全不同的IMF大,即两个信号的相似性更高。根据文献[10-12],通常互相关系数大于0.1时,认为两个信号之间存在一定相关性,基于此,本文将阈值设为m=0.1,即当两个IMF的互相关系数大于m时,说明两个信号间存在频率成分的重叠,此时出现了过分解,令k←k-1,当IMF的互相关系数小于m时,此时的k为合适取值。另外,根据文献[13-14],VMD算法的惩罚因子γ采用默认值2 000,噪声容限τ取0.3以保证实际信号分解的保真度。基于阈值筛选的VMD算法具体步骤如下:
(1)初始化k值(由于内燃机振动激励源较多,振动信号频带较宽,取k=3比较合适);
(2)采用VMD算法对信号进行分解,得到k个IMF;
(3)计算k个IMF之间的互相关系数;
(4)设定阈值m=0.1,如果所有相关系数均小于m,则认为分解不完全,令k←k+1,继续步骤(2)和步骤(3);
(5)当出现相关系数大于m时,则认为出现了过分解,此时令k←k-1,则此时k的取值是比较合适的。
1.2 MHD时频分析
20世纪60年代,Cohen发现众多时频分布只是Wigner-Ville分布的变形[15],这些被称为Cohen类时频分布,Cohen给出了其一般的表达形式:
φ(τ,v)exp(-j2π(tv+τf-uv))dudvdτ
(1)
式中,φ(τ,v)为核函数;t为时间;f为频率;u为积分变量;τ为时移;z、z*为复信号;v为频移。
Wigner-Ville分布可以在式(1)中取核函数φ(τ,v)=1来定义:
(2)
当核函数φ(τ,v)=cos(πτv)时,Wigner-Ville分布即为MHD分布:
cos(πτv)exp(-j2(tv+τf-uv))dudvdτ
(3)
对于多分量信号,根据卷积定理,其MHD会产生交叉干扰项,但是由于MHD满足叠加原理,故可以通过VMD算法将多分量信号分解为一组单分量信号再在时频面进行叠加,使时频图像表征的物理意义更加明确,同时提高信号的时频聚集性。
为分析上述方法的性能,建立一个由三个高斯包络信号复合而成的量纲一多分量信号,信号的时间长度为4 s,采样频率为100 Hz,三个信号的时间和频率中心分别为(1 s,5 Hz)、(1 s,20 Hz)、(3 s,20 Hz),其表达式为
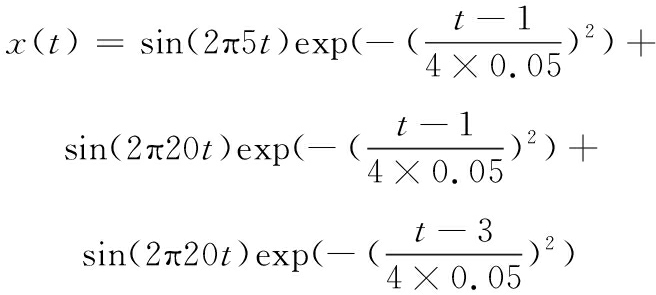
模拟信号的时域波形和MHD分析如图1所示。从时域波形可以看出,模拟信号在时间1 s处存在频率成分重叠。从MHD分析可以看出,在时频面一共出现了四个信号,根据信号表达式,中心分布位于(3 s,5 Hz)的分量信号属于交叉干扰项,是“虚假信号”,其余三个信号是对原信号的正确表达。同时,原有的复合信号由于自项和交叉项叠加,其时频聚集性并不理想。
采用VMD算法对信号进行分解,得到的分量相关系数如表1所示。根据表1结果,当k取3时,IMF1和IMF2相关系数大于设定的阈值(m=0.1)。说明信号出现了过分解,因此k应该取2。令k=2,分解得到的IMF1和IMF2时域信号如图2所示。
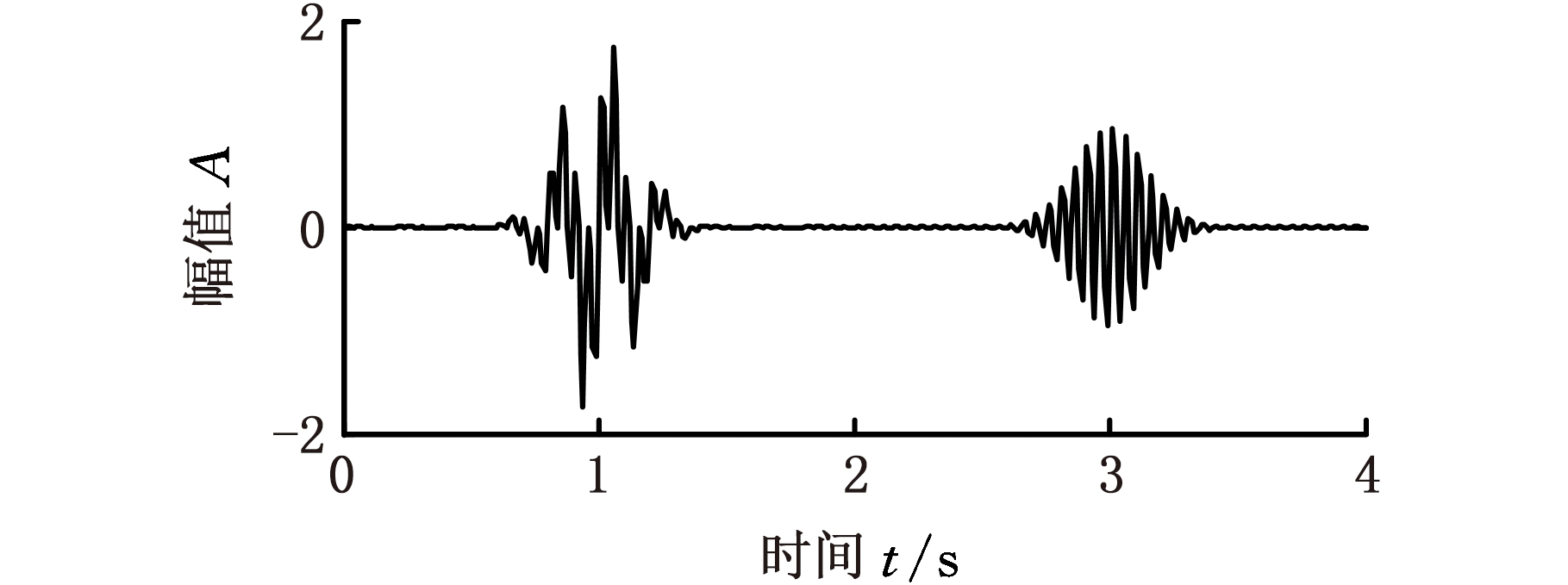
(a)时域波形

(b)MHD时频分布图
图1 模拟信号
Fig.1 Simulation signal
表1 复合信号分量的相关系数
Tab.1 IMFs’ correlation coefficients of composite signal

分解层数kIMF1和IMF2相关系数IMF2和IMF3相关系数20.001 830.161 40.002
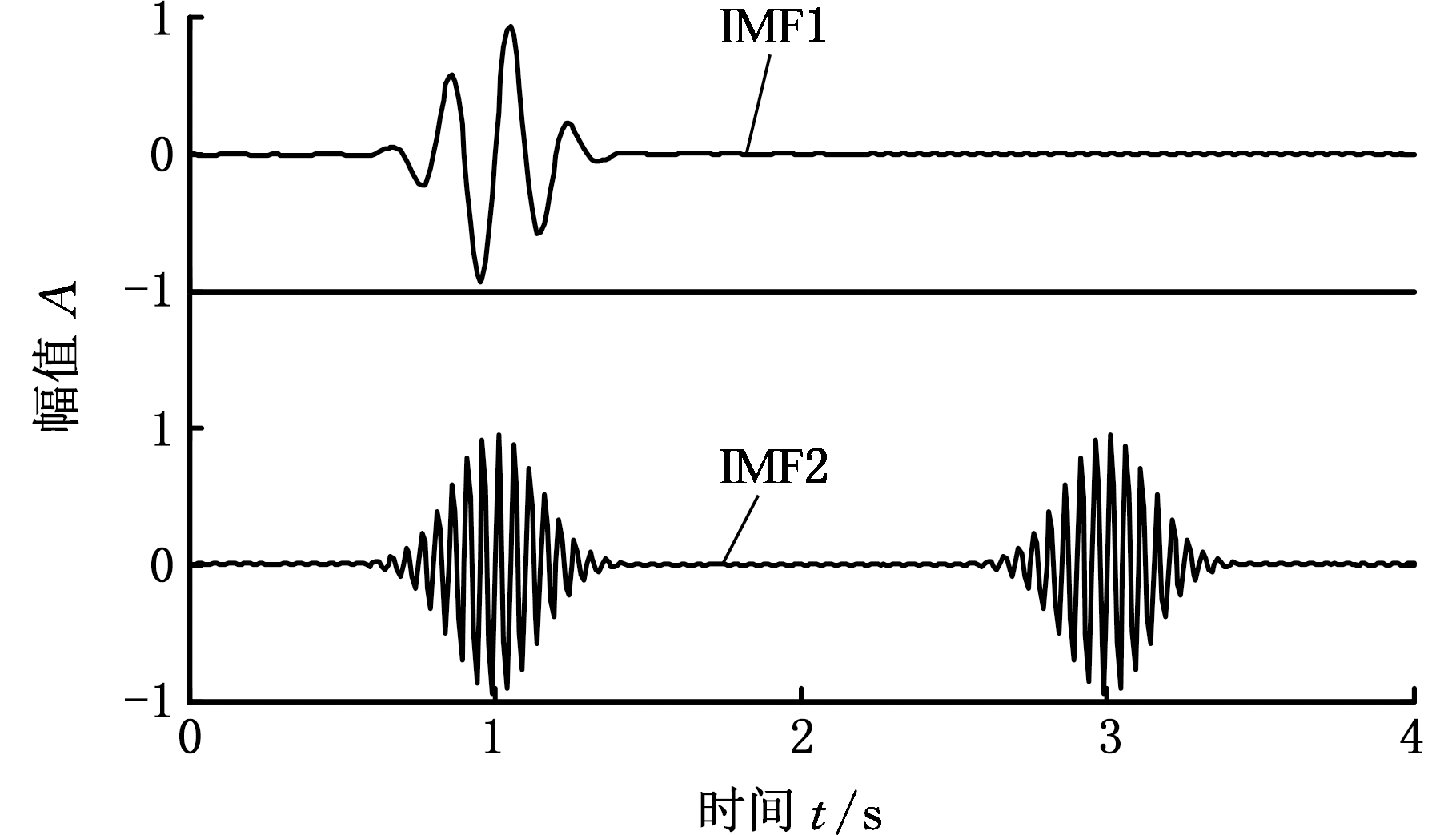
图2 模拟信号的IMF分量
Fig.2 IMFs of simulation signal
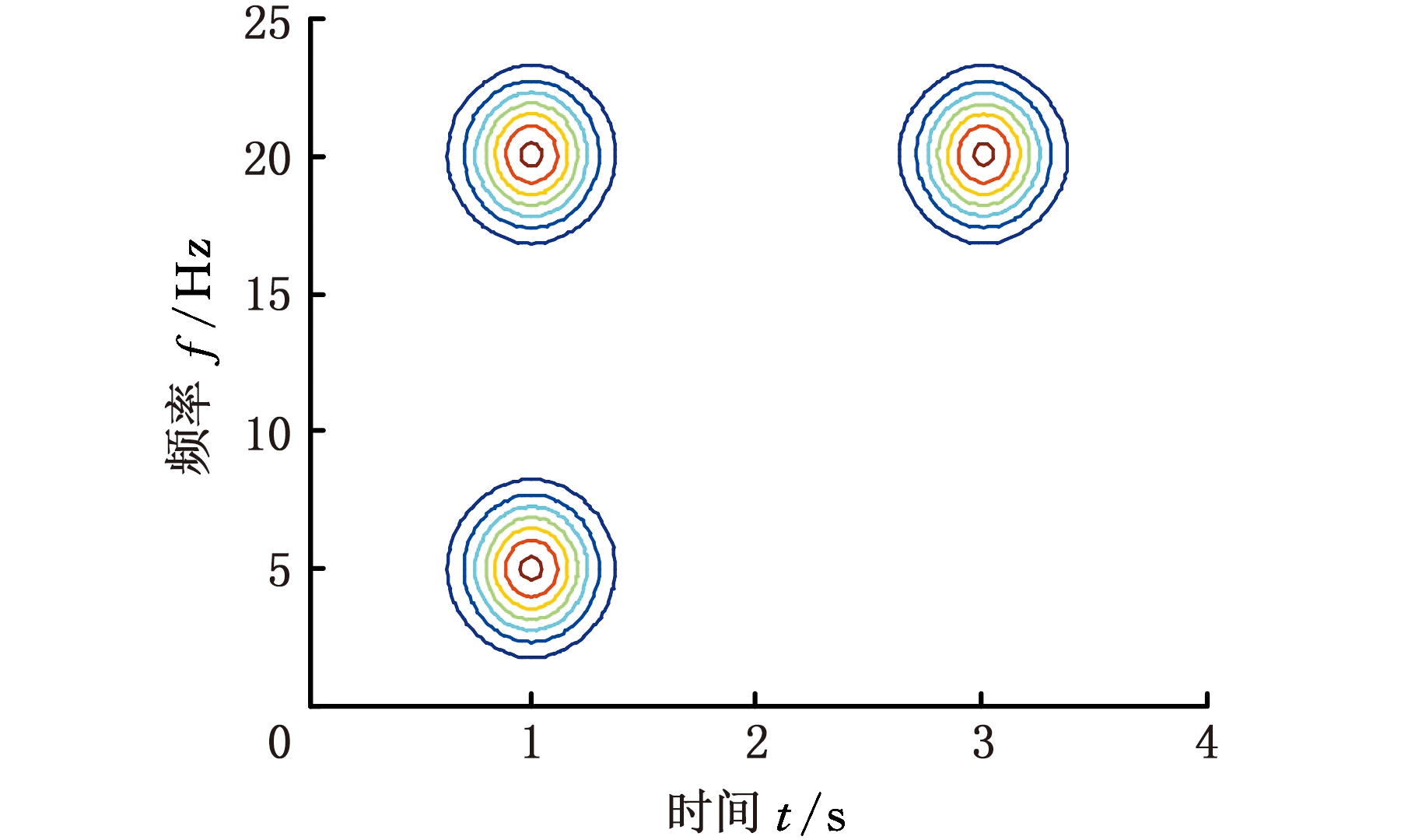
图3 IMF分量线性叠加的MHD时频图
Fig.3 MHD time-frequency distribution by linear
superposition of IMFs
由图2可知,原复合信号在1 s处的两种频率成分(5 Hz和20 Hz)已经被VMD算法分解出来,IMF1和IMF2在任意时间均只存在一种频率成分,均为单分量信号。再对IMF1和IMF2分别进行MHD分析并进行线性叠加得到原复合信号时频图如图3所示。由图3可以看出,干扰信号不仅被较好地抑制,而且原信号的时频聚集性也有所提高,原信号的物理意义变得更加明确。
1.3 振动信号时域参数特征
本文提取了振动信号的6个时域参数特征,相关参数及其对应的表达式如表2所示。
表2 时域特征参数
Tab.2 Time domain characteristic parameters
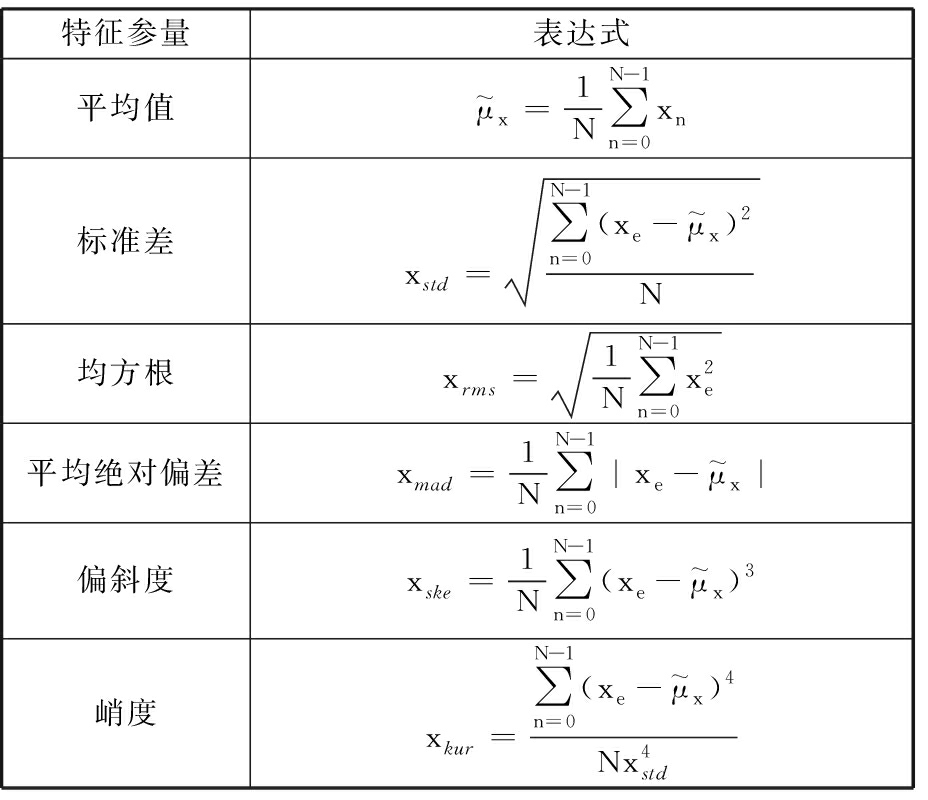
特征参量表达式平均值μ~x=1N∑N-1n=0xn标准差xstd=∑N-1n=0(xe-μ~x)2N均方根xrms=1N∑N-1n=0x2e平均绝对偏差xmad=1N∑N-1n=0|xe-μ~x|偏斜度xske=1N∑N-1n=0(xe-μ~x)3峭度xkur=∑N-1n=0(xe-μ~x)4Nx4std
注:表中N为信号总采样点数;xn为信号在第n个采样点的信号幅值;xe为信号在第e个采样点的信号幅值。
2 局部非负矩阵分解
局部非负矩阵分解(local non-negative matrix factorization,LNMF)方法是在NMF[16]基础上提出的,其根本目的是使分解后的基图像得到更为局部的特征,该方法已经被成功用于人脸识别中[17-18]。LNMF算法是通过对K-L散度目标函数施加基的列正交性约束,减少基向量之间的冗余。LNMF的目标函数如下:
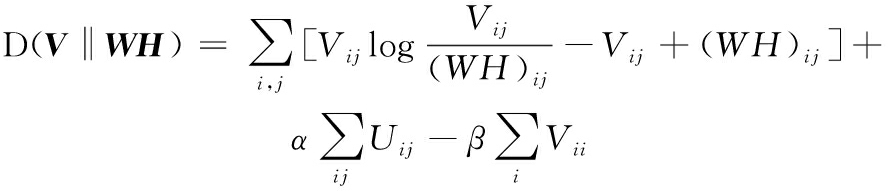
(4)
[Uij]=U=WTW [Vij]=V=HHT
式中,V为大小为M×N的原始矩阵;W为大小为M×r的基矩阵;H为大小为r×N的系数矩阵;α、β为正常数;i=1,2,…,M;j=1,2,…,r。
局部非负矩阵分解主要是对目标函数施加以下三个约束条件,并计算式(4)目标函数的最小值:①![]() 基矩阵W尽量正交,以减少基图像之间的冗余);②
基矩阵W尽量正交,以减少基图像之间的冗余);②![]() 为了使系数矩阵H有最大的稀疏性,以便生成更局部的特征);③maxVii(让基图像有最大的代表性)。其迭代公式如下:
为了使系数矩阵H有最大的稀疏性,以便生成更局部的特征);③maxVii(让基图像有最大的代表性)。其迭代公式如下:
(5)
(6)
(7)
式中,l=1,2,…,N。
使用局部非负矩阵直接对时频分布图像进行特征参数的提取,数据的降维效果明显,简化了计算,避免了复杂的图像运算和传统方法复杂参数的设置问题,具有很好的自适应性。
3 基于改进PSO算法的SVM参数优选
本文采用径向基核函数作为SVM的核函数[19]。在SVM实际应用中,惩罚参数C和核函数参数g的选择比较关键,会对最终的分类结果产生影响,为提高SVM的分类效果,本文采用改进的PSO算法对SVM参数C、g进行优选。
在基本的PSO算法中,粒子根据下式对速度和位置进行更新:
(8)
(9)
式中,w为惯性权重;r为约束因子;c1、c2为学习因子,通常设置为2;ξ、η为区间[0,1]均匀分布的随机数;![]() 为第f个粒子的个体最优解的第d维分量;
为第f个粒子的个体最优解的第d维分量;![]() 为全局最优解的第d维分量;
为全局最优解的第d维分量;![]() 分别为第f个粒子在第k次迭代飞行速度矢量的第d维分量的速度和位置 。
分别为第f个粒子在第k次迭代飞行速度矢量的第d维分量的速度和位置 。
惯性权重w是粒子保持原来速度的系数,其值越大,表示全局搜索能力越强,其值越小,表示局部搜索能力越强。本文使用线性微分递减法改进PSO算法的惯性权重更新方式,其更新公式为
(10)
式中,wmax为最大权重值;wmin为最小权重值;h为当前迭代次数;T为最大迭代次数。
在进化前期,w的减小趋势缓慢,全局搜索能力强,有利于找到很好的优化粒子;在进化后期w的减小趋势加快,可以使算法快速收敛,并在后期提高搜索精度。参数优选的SVM算法流程如下:
(1)设置粒子种群规模和最大迭代次数,本文分别设定为100和200;设定参数C、g的搜索范围;初始化粒子的位置和速度、局部最优解和全局最优解。
(2)计算每个粒子的适应度,本文将SVM识别准确率定为适应度。
(3)根据式(8)、式(9)更新粒子的速度和位置,根据式(10)更新权重系数。
(4)将每个粒子的适应度值和个体极值比较,如果较好,则替换个体极值。
(5)将每个粒子的适应度值和全局极值比较,如果较好,则替换全局极值。
(6) 达到最大迭代次数时结束算法,未达到则跳至步骤(2)。
4 内燃机故障诊断实例
4.1 故障诊断流程及试验数据采集
本文提出的内燃机故障诊断方法步骤如下:首先采集内燃机运行过程中8种工况的振动信号,然后采用基于阈值筛选的VMD和MHD对振动信号进行时频分析,再采用LNMF对时频图像进行特征提取,再将时域特征参数与LNMF提取的图像特征进行融合,最后用改进的SVM进行分类识别,完成内燃机的故障诊断,诊断流程如图4所示。

图4 内燃机故障诊断流程
Fig.4 Process of IC engine fault diagnosis
试验数据采集自车载BF4L10011F型柴油机,试验中采用AVL油压传感器采集柴油机喷油管压力,PCB(printed circuit board)振动传感器采集柴油机气门机构附近的振动情况,其中PCB振动传感器采样频率为25 kHz,根据文献[20-22]的试验设定,设置柴油机空载运行,转速为1 500 r/min。试验现场如图5所示。

图5 试验现场
Fig.5 Test environment
试验通过改变内燃机配气机构进气门、排气门的间隙大小可以设置不同的故障,工况具体设置情况如表3所示。
表3 8种试验工况设置
Tab.3 8 test working conditions settings

工况编号工作状态进气门间隙(mm)排气门间隙(mm)1气门间隙正常0.30.32排气门间隙过小0.30.063排气门间隙过大0.30.54排气门漏气0.3(开口4×1)5模拟新气门0.3(新气门)6进气门、排气门均过小0.060.067进气门过小、排气门过大0.060.58进气门、排气门均过大0.50.5
4.2 多工况振动信号时频分析
以工况1(正常工况)为例,对采集的振动信号进行VMD分解,k取不同值所对应的分量的相关系数如表4所示。
表4 正常工况振动信号分量的相关系数
Tab.4 IMFs’ correlation coefficients of normalworking condition’s vibration signal

分解层数kIMF1和IMF2相关系数IMF2和IMF3相关系数IMF3和IMF4相关系数20.036 230.052 70.074 540.089 80.064 60.150 450.097 90.036 00.206 8
从表4中可以看出,对于工况1,当分解层数k>3时,分量IMF3和IMF4的相关系数均大于阈值0.1,所以取分解层数k=3是比较合适的,此时对信号的分解效果如图6所示。

(a)时域波形 (b)频域波形
图6 工况1的信号分解结果
Fig.6 Signal decomposition result of working condition 1
从分量信号的频域波形来看,三个信号频带集中在0~2 kHz、4~6.5 kHz和6.5~8 kHz。根据文献[23],这三个频带分别是由内燃机缸内燃烧后段、燃烧主段和进排气门开闭引起的振动导致的,这也说明本算法对信号分解符合客观事实。
同时,为了说明改进的VMD算法对其他工况的适用性,再以工况3为例,采用改进的VMD算法对其振动信号进行分解。
对于工况3(排气门间隙过大),k取不同值所对应的分量的相关系数如表5所示。
表5 工况3振动信号分量的相关系数
Tab.5 IMFs’ correlation coefficients ofworking condition 3’s vibration signal

分解层数kIMF1和IMF2IMF2和IMF3IMF3和IMF420.007 430.033 20.017 540.032 90.012 70.141 6
对比图7、图8可以看出,当k取4时,IMF3和IMF4的中心频率明显较其他分量更为接近,产生了频率混叠,因此k取3更加合适,这和从表5得出的k值是一致的。

(a)时域波形 (b)频域波形
图7 k=3时工况3的信号分解结果
Fig.7 Signal decomposition result of working
condition 3 when k=3

(a)时域波形 (b)频域波形
图8 k=4时工况3的信号分解结果
Fig.8 Signal decomposition result of working
condition 3 when k=4
运用该方法对其余几种工况进行分析,大量的试验结果表明基于阈值筛选的VMD算法对信号分解合理,有利于对信号的进一步研究。对8种工况的内燃机振动信号进行VMD分解和MHD分析,结果如图9~图16所示。
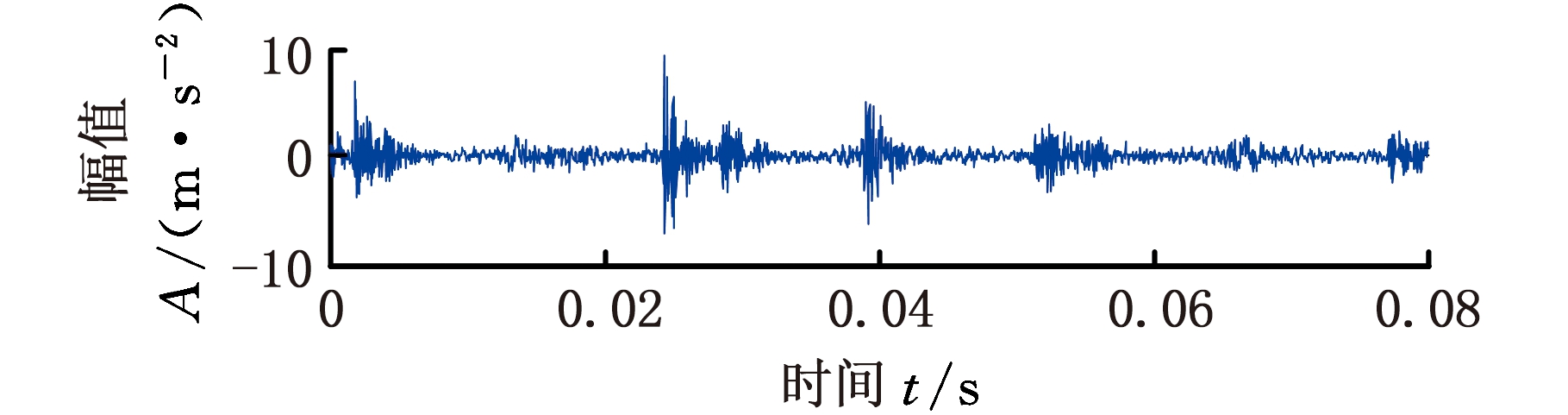
(a)时域波形

(b)频域波形

(c)时频相平面图
图9 VMD-MHD分析结果(工况1)
Fig.9 VMD-MHD analysis result(working condition 1)

(a)时域波形

(b)频域波形

(c)时频相平面图
图10 VMD-MHD分析结果(工况2)
Fig.10 VMD-MHD analysis result(working condition 2)

(a)时域波形

(b)频域波形

(c)时频相平面图
图11 VMD-MHD分析结果(工况3)
Fig.11 VMD-MHD analysis result(working condition 3)

(a)时域波形

(b)频域波形

(c)时频相平面图
图12 VMD-MHD分析结果(工况4)
Fig.12 VMD-MHD analysis result(working condition 4)
BF4L10011F型内燃机为四冲程内燃机,且试验设定内燃机转速为1 500 r/min,因此其一个工作循环时间为0.08 s,气门动作和具体时间的对应情况如表6所示。

(a)时域波形
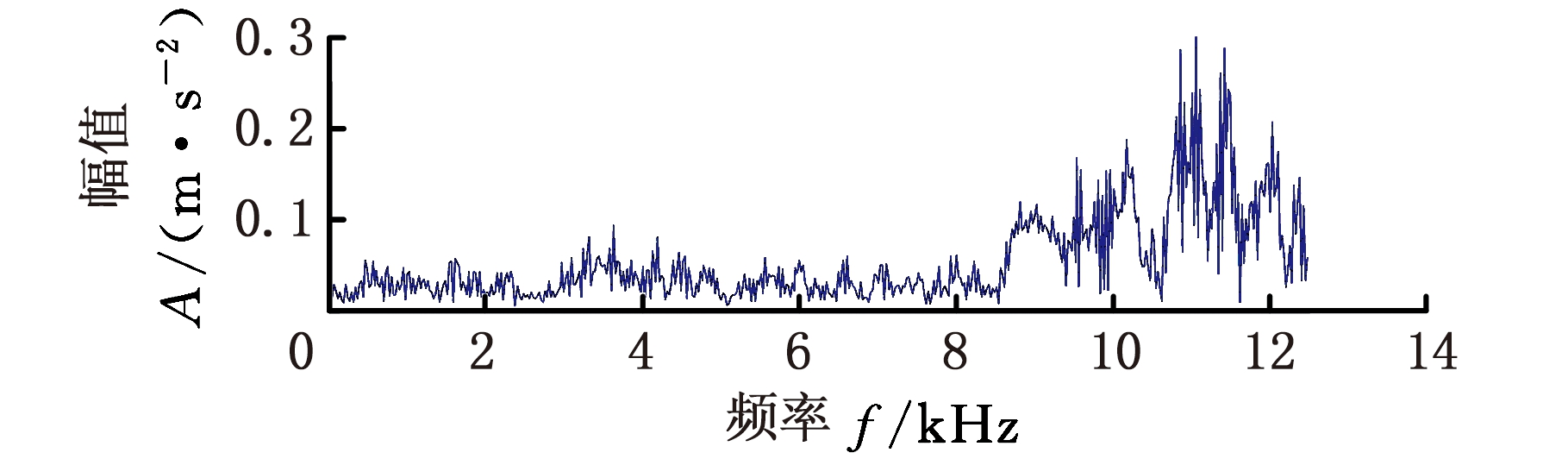
(b)频域波形

(c)时频相平面图
图13 VMD-MHD分析结果(工况5)
Fig.13 VMD-MHD analysis result(working condition 5)

(a)时域波形

(b)频域波形
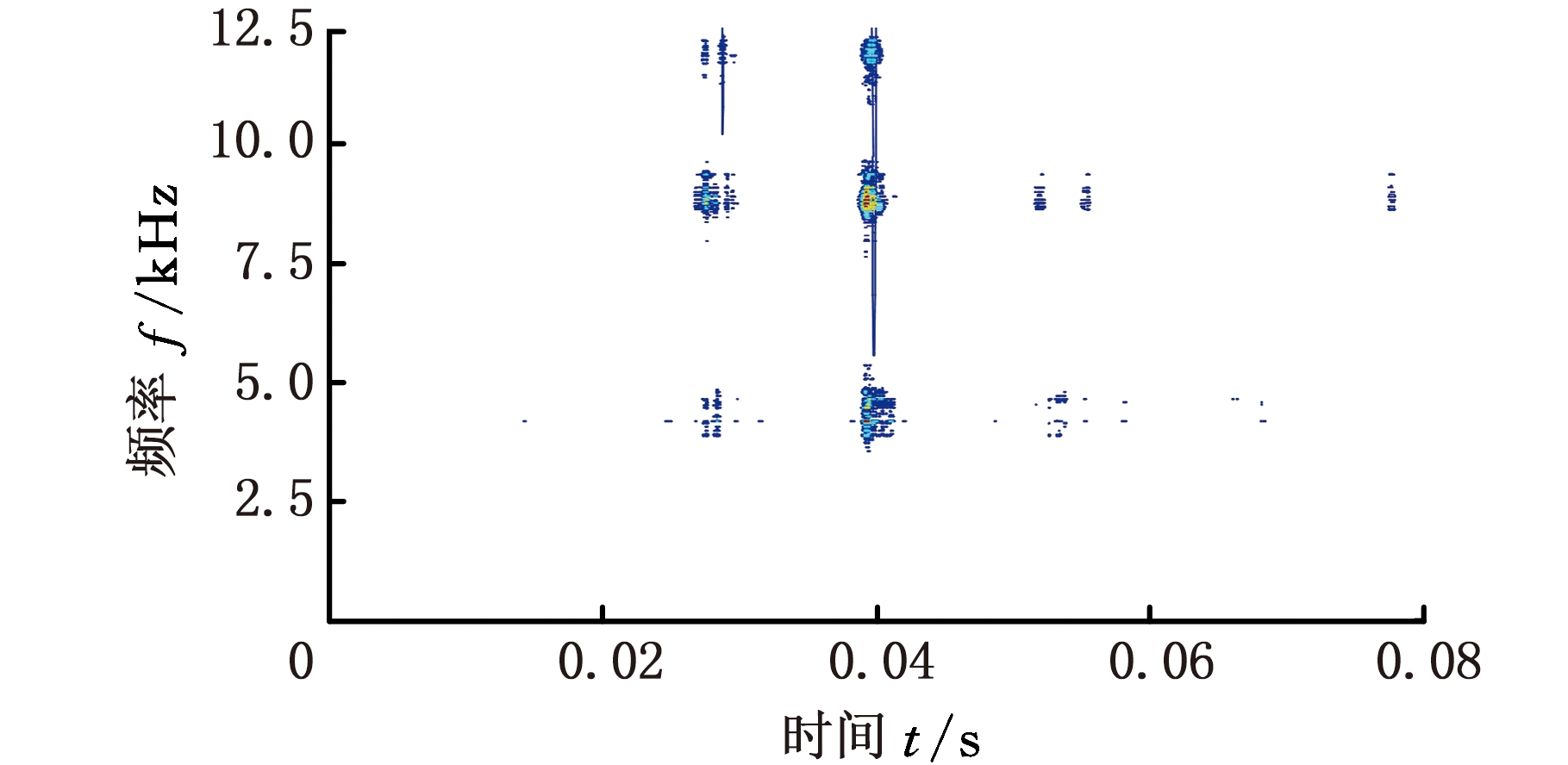
(c)时频相平面图
图14 VMD-MHD分析结果(工况6)
Fig.14 VMD-MHD analysis result(working condition 6)
从8种工况的时域波形、频域波形及其对应时频图来看,除了正常工况外,故障工况在高频部分(10~12 kHz)均存在能量分布,这说明内燃机气门间隙故障主要引起的是高频振动。对比8种工况点火时刻的振动情况可以看出,只有正常工况冲击分量最大,这说明混合气体燃烧效率最高。同时,内燃机气门间隙故障对缸内气体燃烧影响比较大,当排气门间隙过大时会导致气门早关、迟开,从而使排气时间变短,废气不能充分排出,进一步会导致工质更新恶化,影响燃烧效率;排气门间隙过小则会导致气门迟关、早开,进一步会导致气门受热膨胀后密封不严,燃烧不良,增加油耗。气门间隙故障不仅会导致内燃机气体燃烧不良,也会影响气门落座时对于内燃机缸盖的冲击,对比工况2、3可以清楚地看到,由于工况3排气门间隙(0.5 mm)远大于工况2排气门间隙(0.06 mm),在排气门关闭时工况3的冲击振动要远大于工况2的冲击振动。通过上文的分析可知,时频图能够清晰表明内燃机在不同工况下振动信号频率分量的构成情况,较好地刻画不同故障的时频特征,将之用于分类器进行分类识别是完全可行的。

(a)时域波形

(b)频域波形

(c)时频相平面图
图15 VMD-MHD分析结果(工况7)
Fig.15 VMD-MHD analysis result(working condition 7)

(a)时域波形

(b)频域波形

(c)时频相平面图
图16 VMD-MHD分析结果(工况8)
Fig.16 VMD-MHD analysis result(working condition 8)
表6 内燃机工作循环
Tab.6 IC engine working cycle
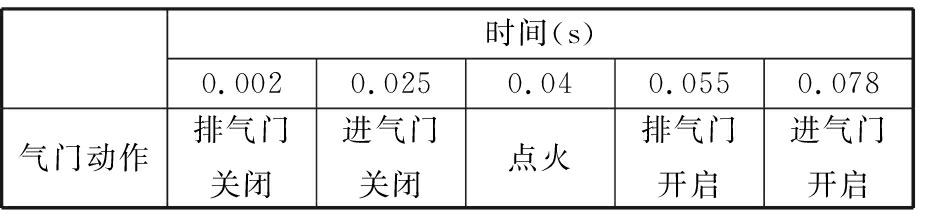
时间(s)0.0020.0250.040.0550.078气门动作排气门关闭进气门关闭点火排气门开启进气门开启
4.3 LNMF特征提取
使用LNMF进行特征提取的具体流程如下:
(1)对预处理所得到的时频矩阵进行重排操作,将每个时频矩阵由90×120维变形为10 800×1维列向量;
(2)从8类工况时频分布图中每一类随机选取30幅共240幅,组成LNMF样本集(矩阵)V,V的维数为10 800×240;
(3)对样本集V进行LNMF分解,可得特征矩阵W,W的维数为10 800×r。r表示特征维数,它的取值对LNMF分解的结果和后续的识别精度有较大影响;
(4)将所有时频图像向基矩阵W投影,可得480个系数向量H,H的维数为r×1。系数向量H代表了它所对应的时频图像,此时将每一类图像前30幅作为训练集,后30幅作为测试集。
4.4 特征融合
对每一幅时频图像对应的振动信号进行时域特征参数计算,根据1.3节,每个振动信号可得到6个时域特征参数,此时,将特征参数与4.3节中提取的特征向量H进行串行拼接,则每一个振动信号的特征向量H的维数被扩展为r+6。
由于LNMF提取的时频图像特征和振动信号的时域特征参数在数值上悬殊很大,为避免不同特征之间的数量级差别对识别结果产生影响,要对提取的特征进行标准化处理,常用的处理方式有以下两种。
(1)最大最小法:
式中,xmin为数据序列的最小值;xmax为数据序列的最大值。
(2)平均数方差法:
式中,xmean为数据序列的均值,xvar为数据序列的方差。
本文采用第一种数据标准化方法。
4.5 结果分析
首先,采用默认参数设置(C=1,g =1/r)的SVM对LNMF单独提取的时频图像特征和融合时域参数后的特征分别进行分类识别,识别准确率是指测试集中8种工况被分类器正确识别为其对应工况的总数量与测试集信号总数量的比值。当特征维数r取不同值时,对应的识别结果如图17所示。
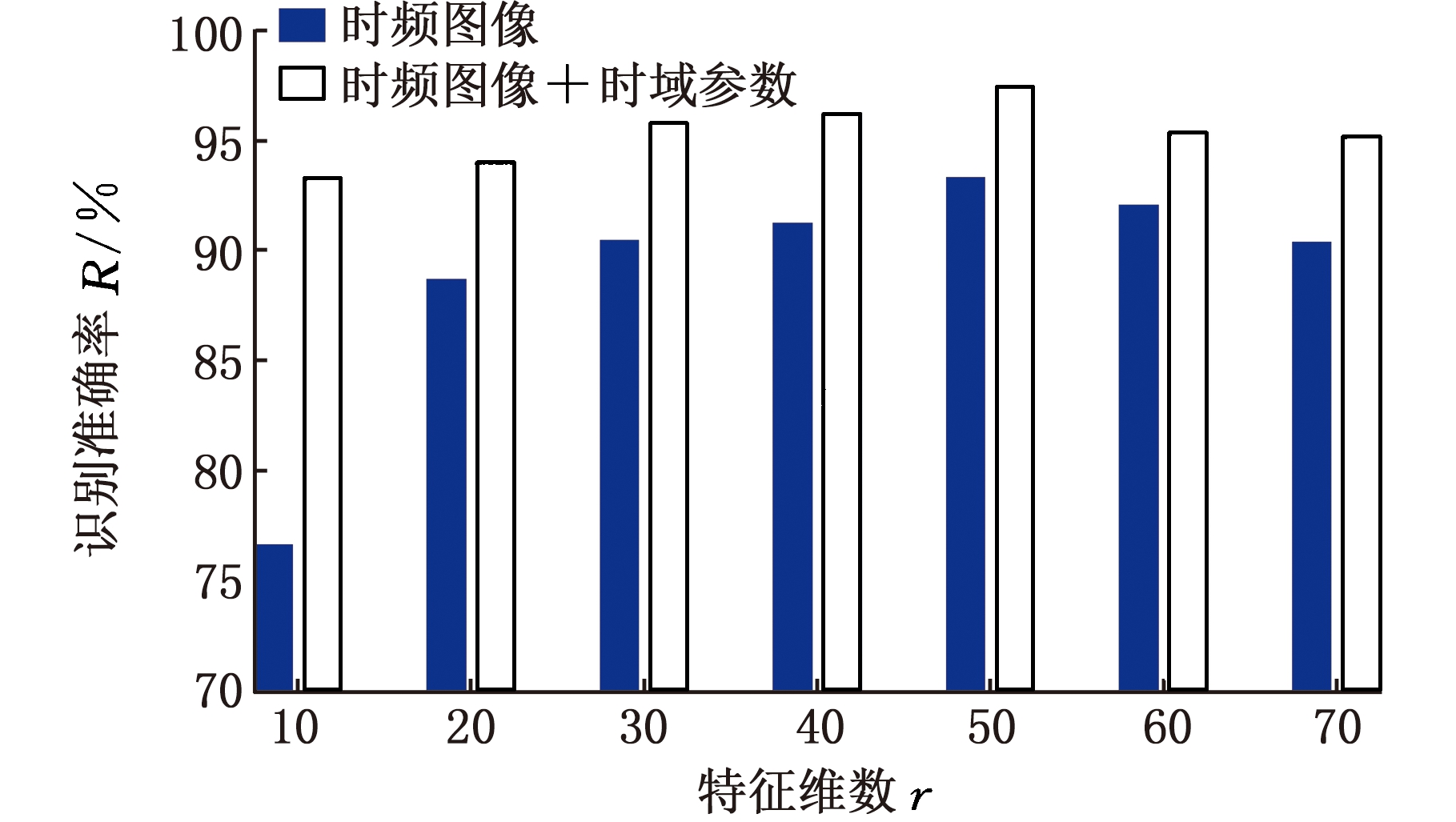
图17 识别结果
Fig.17 Recognition results
从图17中可知,单独使用LNMF提取的时频图像特征进行分类的准确率明显不如时频图像特征融合信号时域参数的准确率高,但都在LNMF特征维数取50时达到最大,此时,SVM对单独特征识别率为93.3%,对融合特征识别准确率为97.5%。同时,SVM的识别准确率并没有始终随特征维数的增大而增大,这是因为当特征维数较小时,特征向量包含的图像信息不全,对不同工况时频图像的区分能力存在一定欠缺,导致分类准确率不高,当特征维数过大时则会导致特征向量信息冗余,也不利于最终识别分类的准确率。
同时,从图17中来看,特征维数r=50时,两种情况的识别准确率都是最高的,这说明用LNMF算法提取特征时r取50是最合适的。在此基础上,通过对SVM进行参数寻优来进一步提高识别准确率,本文分别采用原始PSO算法和改进PSO算法对SVM进行参数寻优,结果如表7所示。
表7 识别准确率
Tab.7 Recognition accuracy %

分类方法识别准确率PSO+SVM98.75改进PSO+SVM99.17
从表7可以看出,使用改进PSO算法对SVM进行参数寻优可以得到最高的识别准确率,为99.17%,这是因为改进的惯性权重随着算法的迭代次数增加不断减小,算法在后期增强了局部搜索能力,提高了搜索精度。此时对应的C=75.22,g=0.008,其适应度进化曲线见图18。

图18 适应度进化曲线
Fig.18 Adaptive evolution curve
可以看到,当迭代次数达到120时,识别准确率取得了最优解99.17%,相比于默认参数情况下97.5%的识别准确率,改进算法有效提升了SVM的分类效果。为了进一步说本文所提算法的优越性,同时给出常用的最近邻分类器(nearest neighborhood classifier,NNC)和本文分类算法在直接对振动信号进行MHD分析+LNMF特征提取、基于改进的VMD+MHD分析+LNMF特征提取和特征融合三种情况下的分类结果(LNMF特征维数均为50),对比结果如表8所示。
表8 识别准确率
Tab.8 Recognition accuracy %
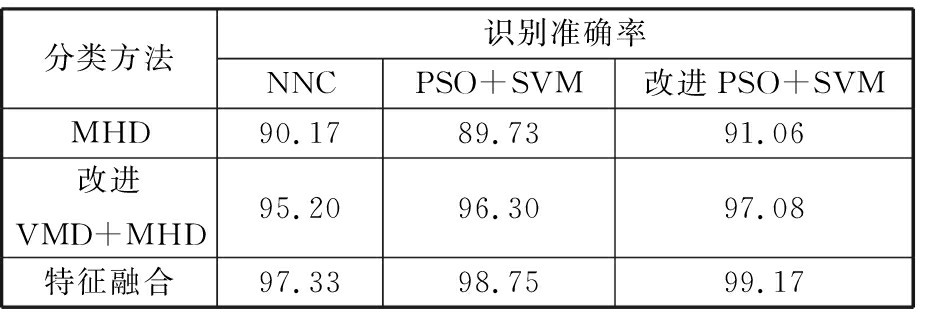
分类方法识别准确率NNCPSO+SVM改进PSO+SVMMHD90.1789.7391.06改进VMD+MHD95.2096.3097.08特征融合97.3398.7599.17
从表8中纵向对比结果来看,无论采用哪种分类方法,直接对振动信号进行MHD时频分析,再用LNMF提取特征的分类效果都是最差的,这是因为直接对信号进行时频分析会产生交叉干扰项,降低信号时频聚集性,从而导致不同工况时频图像差异性不够显著,影响了分类器的识别分类;采用改进的VMD+MHD分析对交叉干扰项有明显的抑制作用,能够提升分类效果;而特征融合在时频特征的基础上融合了信号的时域参数特征,能够进一步提高不同工况信号的差异性,使得分类结果进一步提高。从横向对比来看,在3种信号特征情况下,本文提出的改进PSO+SVM分类算法均取得了最优识别效果,说明了本文方法的优越性。
5 结论
(1)基于阈值筛选的VMD算法能够对复杂的多分量信号进行有效、合理的分解,有效抑制Cohen类时频分布中存在的交叉干扰项,提高信号的时频聚集性。该方法与MHD结合对内燃机振动信号进行时频表征可以清晰刻画信号中冲击分量的时间和频率特性,较好反映信号的物理特性。
(2)用LNMF提取的特征与信号时域参数特征融合后的特征向量比单独使用LNMF提取的特征向量有更高的识别准确率,在SVM默认参数设置下,前者最高为97.5%,后者最高为93.3%。
(3)对SVM进行参数优选能够进一步提高识别准确率,其中PSO+SVM最高识别准确率为98.75%,改进PSO+SVM最高识别准确率为99.17%。
(4)本文改进PSO+SVM分类算法的识别准确率要高于传统NNC分类器的识别准确率。
[1] FENG Zhipeng, LIANG Min, CHU Fulei. Recent Advances in Time-frequency Analysis Methods for Machinery Fault Diagnosis: a Review with Application Examples[J]. Machanical Systems and Signal Processing, 2013, 38(1):165-205.
[2] 刘洋,刘晓波,梁珊. 基于傅里叶分解方法的航空发动机转子故障诊断[J]. 中国机械工程, 2019, 30(18):2156-2163.
LIU Yang, LIU Xiaobo, LIANG Shan. Aeroengine Rotor Fault Diagnosis Based on Fourier Decomposition Method[J]. China Mechanical Engineering, 2019, 30(18):2156-2163.
[3] SAMIMY B, RIZZONI G. Engine Knock Analysis and Detection Using Time-frequency Analysis[J]. SAE Transactions, 1996,105(3):764-775.
[4] 蒋平, 贾平民, 许飞云, 等. Wigner-Ville分布在机械故障诊断中的研究[J]. 制造技术与机床, 2004(7):24-28.
JIANG Ping, JIA Pingmin, XU Feiyun, et al. The Research of Wigner-Ville Distribution in Machine Fault Diagnosising[J]. Manufacturing Technology & Machine Tools, 2004(7):24-28.
[5] 蔡艳平, 李艾华, 王涛, 等. 基于时频谱图与图像分割的柴油机故障诊断[J]. 内燃机学报, 2011, 29(2):181-186.
CAI Yanping, LI Aihua, WANG Tao, et al. IC Diesel Engine Fault Diagnosis Based on Time-frequency Spectrum Image and Image Segmentation [J]. Transactions of CSICE, 2011, 29(2):181-186.
[6] 李红坤, 周帅, 黄文宗. 基于时频图像特征提取的状态识别方法研究与应用[J]. 振动与冲击, 2010, 29(7):184-188.
LI Hongkun, ZHOU Shuai, HUANG Wenzong.Time-frequency Image Feature Extraction for Machine Condition Classification and Its Application[J]. Journal of Vibration and Shock, 2010, 29(7):184-188.
[7] 王科俊, 左春婷. 非负矩阵分解特征提取技术的研究进展[J]. 计算机应用研究, 2014, 31(4):970-975.
WANG Kejun, ZUO Chunting. Improvements of Non-negative Matrix Factorization for Image Extraction[J]. Application Research of Computers, 2014, 31(4):970-975.
[8] DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3):531-544.
[9] 姜万录,王浩楠,朱勇,等. 变分模态分解消噪与核模糊C均值聚类相结合的滚动轴承故障识别方法[J]. 中国机械工程, 2017, 28(10):1215-1220.
JIANG Wanlu, WANG Haonan, ZHU Yong, et al. Integrated VMD Denoising and KFCM Clustering Fault Identification Method of Rolling Bearings[J]. China Mechanical Engineering, 2017, 28(10):1215-1220.
[10] 费鸿禄, 刘梦, 曲广建, 等. 基于集合经验模态分解-小波阈值方法的爆破振动信号降噪方法[J]. 爆炸与冲击, 2018, 38(1):112-117.
FEI Honglu, LIU Meng, QU Guangjian, et al. A Method for Blasting Vibration Signal Denoising Based on Ensemble Empirical Mode Decomposition-wavelet Threshold[J]. Explosion and Shock Waves, 2018, 38(1):112-117.
[11] 姜建国, 王庆. 基于MEEMD和峭度-相关系数电机轴承故障诊断[J]. 电气传动, 2018, 37(1):65-70.
JIANG Jianguo, WANG Qing. Motor Bearing Fault Diagnosis Based on MEEMD and Kurtosis-Relevant Coeffcient[J]. Electrical Drive, 2018, 37(1):65-70.
[12] 李从善, 刘天琪, 李兴源, 等. 基于排列熵算法的电力系统故障信号分析[J]. 电子科技大学学报, 2015, 44(2):233-238.
LI Congshan, LIU Tianqi, LI Xingyuan, et al. Power System Fault Signal Analysis Based on Permutation Entropy Algorithm[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(2):233-238.
[13] 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13):3358-3365.
LIU Changliang, WU Yingjie, ZHEN Chenggang. Rolling Bearing Fault Diagnosis Based on Variational Mode Decomposition and Fuzzy C Means Clusters[J]. Proceedings of the CSEE, 2015, 35(13):3358-3365.
[14] 郑近德, 潘海洋, 杨树宝, 等. 广义变分模态分解方法及其在变工况齿轮故障诊断中的应用[J]. 振动工程学报, 2017, 30(3):502-509.
ZHENG Jinde, PAN Haiyang, YANG Shubao, et al. Generalized Variational Mode Decomposition and Its Applications to Gearbox Fault Diagnosis under Variable Conditions[J]. Journal of Vibration Engineering, 2017, 30(3):502-509.
[15] 葛哲学, 陈仲生. MATLAB时频分析技术及其应用[M]. 北京:人民邮电出版社, 2006:16-17.
GE Zhexue, CHEN Zhongsheng.MATLAB Time-frequency Analysis Technology and Application[M]. Beijing:Posts & Telecom Press, 2006:16-17.
[16] LEE D D, SEUNG H S. Learning the Parts of Objects by Non-negative Matrix Factorization [J]. Nature, 1994, 401(6755):788-791.
[17] 刘昱昊.基于非负矩阵分解算法的人脸识别技术的研究[D]. 长春:吉林大学,2014.
LIU Yuhao. Research on NMF-based Algorithms Applying to Face Recognition[D]. Chuangchun:Jilin University, 2014.
[18] 袁宝华, 王欢,任明武. LBP与LNMF特征融合的人脸识别[J].计算机工程与应用, 2013, 49(5):166-169.
YUAN Baohua, WANG Huan, Ren Mingwu. Fusing Local Binary Pattern and LNMF of Face Recognition[J]. Computer Engineering and Application, 2013, 49(5):166-169.
[19] 何行, 夏水斌, 张芹, 等.基于改进PSO-SVM算法的电能质量扰动分类[J]. 电力电容器与无功补偿, 2019, 40(2):119-124.
HE Xing, XIA Shuibin, ZHANG Qin, et al. Power Quality Disturbances Classification Based on Improved PSO and SVM Algorithm[J]. Power Capacitor & Reactive Power Compensation, 2019, 40(2):119-124.
[20] 吴震宇, 袁惠群. 蚁群支持向量机在内燃机故障诊断中的应用研究[J]. 振动与冲击, 2009, 28(3):83-86.
WU Zhenyu, YUAN Huiqun. Fault Diagnosis of an Engine with an Ant Colony Support Vector Machine[J]. Journal of Vibration and Shock, 2009, 28(3):83-86.
[21] 刘永斌, 何清波, 孔凡让, 等. 基于PCA和SVM的内燃机故障诊断[J]. 振动、测试与诊断, 2012, 32(2):250-255.
LIU Yongbin, HE Qingbo, KONG Fanrang, et al.Fault Diagnosis of Internal Engine Using PCA and SVM[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(2):250-255.
[22] 王祝平, 王为, 李小昱, 等. 基于EMD与神经网络的内燃机气门间隙故障诊断[J]. 农业机械学报, 2007, 38(12):133-136.
WANG Zhuping, WANG Wei, LI Xiaoyu, et al.Fault Diagnosis of Engine Valve Based on EMD and Artificial Neural Network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(12):133-136.
[23] 蔡艳平, 成曙, 李艾华. 柴油机振动机理及特性研究[J]. 控制工程, 2007, 14(增刊1):185-188.
CAI Yanping, CHENG Shu, LI Aihua. On Vibration and Characteristic for Diesel Engine[J]. Control Engineering of China, 2007, 14(S1):185-188.
